【牛客】小w的魔术扑克 (并查集?? 树状数组)
题目描述
小w喜欢打牌,某天小w与dogenya在一起玩扑克牌,这种扑克牌的面值都在1到n,原本扑克牌只有一面,而小w手中的扑克牌是双面的魔术扑克(正反两面均有数字,可以随时进行切换),小w这个人就准备用它来出老千作弊。小w想要打出一些顺子,我们定义打出一个l到r的顺子需要面值为从l到r的卡牌各一张。小w想问问你,他能否利用手中的魔术卡牌打出这些顺子呢?
输入描述:
首先输入一行2个正整数n,k,表示牌面为1~n,小w手中有k张魔术扑克牌。
然后输入k行,每行两个数字,表示卡牌的正面和反面的面值。
接下来输入一行一个正整数q,表示q组查询,然后每组占一行查询输入两个整数l,r。表示查询小w能否打出这么一个l到r的顺子。
输出描述:
对于输出"Yes"表示可以,"No"表示不可以。(不含引号)
每个查询都是独立的,查询之间互不影响。
示例1
输入
5 3
1 2
2 3
4 4
3
1 2
2 4
1 4
输出
Yes
Yes
No
说明
对于顺子1~2,可以选择第一张卡牌作为'1'使用,选择第二张卡牌作为'2'使用。
对于顺子2~4,可以选择第一张卡牌作为'2'使用,选择第二张卡牌作为'3'使用,选择第三张卡牌作为'4'使用。
对于顺子1~4,由于牌的数目都不够,显然无法打出。
示例2
输入
4 3
1 1
2 2
4 4
3
1 2
1 4
4 4
输出
Yes
No
Yes
分析
一开始想用dp,贪心,二分图之类的始终没想出来,后来强行逼自己往图论方面想才想到了解法
对于任意一张卡片我们可以把它看成一条边,将两个值连起来,而选择哪个值相当于给这条边定向
就拿样例1举例子,样例1的图如下
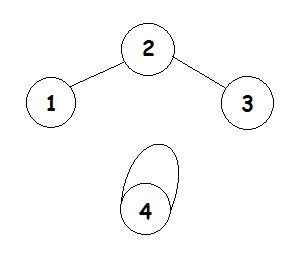
每张牌选哪个值,对应的那条边就指向哪个值
比如现在我们要凑出顺子[2,4],显然1不在顺子里,2在顺子里,那么连接1,2的边肯定指向2
那么结果如图
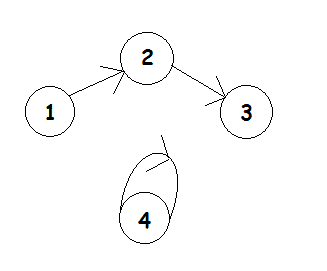
进而我们得出一个结论,在同一个联通块里面的数值,假设连通块大小为n,如果这个连通块是一棵树,那么连通块里面最多能取n-1个点(只有n-1条边)。
而且我们可以决定这n-1个点分别是哪些(只要找到不取的点,将它周围的边都指向其它节点,依次推下去即可
如果这个联通块中存在环,那么这个连通块中的所有点都可以取,如图
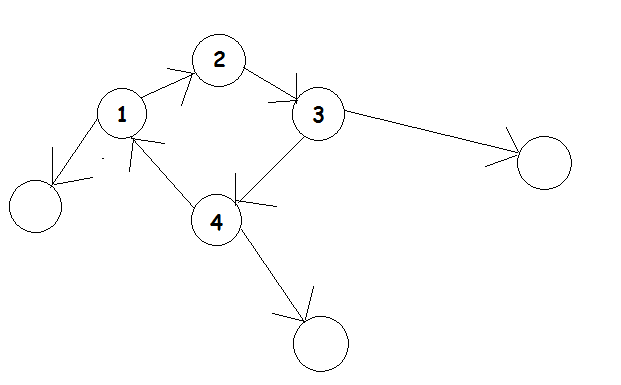
那么对于每棵树,我们求出它最小节点和最大节点,如果询问区间同时包含了最小节点和最大节点,就相当于包含了这棵树,
这个时候因为肯定有1个点取不到,所以肯定完成不了
所以对于每棵树求出它的最小节点,最大节点,这两个节点形成一段区间,包含这段区间的询问区间就无法完成
接下来就相当于要判断询问区间是否包含这些区间
如果一段区间[l,r]包含另一端区间[l1,r1],那么一定满足l<l1且r1<r。
在l1位置插入值r1,在l位置查询后缀最小值,如果该值小于r,那么一定存在左端点在l后面,右端点在r左边的区间,即被包含的区间
这个可以用数组维护,也可以O(n)扫过去预处理。
Code
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=100005;
int n,k,Q,mn[maxn],mx[maxn],bit[maxn],ori[maxn],vis[maxn],cnt[maxn][2];
int find(int x){return !ori[x]?x:ori[x]=find(ori[x]);}
void add(int x,int k){for(;x;x-=(x&-x))bit[x]=min(bit[x],k);}
int que(int x){int ret=bit[0];for(;x<=n;x+=(x&-x))ret=min(ret,bit[x]);return ret;}
int main()
{
scanf("%d%d",&n,&k);for(int i=1;i<=n;i++)cnt[i][0]=1;
for(int i=1,s1,s2;i<=k;i++)
{
scanf("%d%d",&s1,&s2);
s1=find(s1);s2=find(s2);
if(s1==s2){cnt[s1=s2][1]++;continue;}
cnt[s1][0]+=cnt[s2][0];cnt[s1][1]+=cnt[s2][1]+1;ori[s2]=s1;
}
for(int i=1,s;i<=n;i++)if(!vis[s=find(i)])vis[s]=1,mx[s]=i,mn[s]=i;else mx[s]=i;
memset(vis,0,sizeof vis);memset(bit,0x3f,sizeof bit);
for(int i=1,s;i<=n;i++)if(!vis[s=find(i)]){vis[s]=1;if(cnt[s][0]>cnt[s][1])add(mn[s],mx[s]);}
scanf("%d",&Q);
for(int i=1,l,r;i<=Q;i++)
{
scanf("%d%d",&l,&r);
if(r>=que(l))puts("No");else puts("Yes");
}
}

