【CSP模拟赛】奇怪的队列(树状数组 &二分&贪心)
题目描述
nodgd的粉丝太多了,每天都会有很多人排队要签名。
今天有n个人排队,每个人的身高都是一个整数,且互不相同。很不巧,nodgd今天去忙别的事情去了,就只好让这些粉丝们明天再来。同时nodgd提出了一个要求,每个人都要记住自己前面与多少个比自己高的人,以便于明天恢复到今天的顺序。
但是,粉丝们或多或少都是有些失望的,失望使她们晕头转向、神魂颠倒,已经分不清楚哪一边是“前面”了,于是她们可能是记住了前面比自己高的人的个数,也可能是记住了后面比自己高的人的个数,而且他们不知道自己记住的是哪一个方向。
nodgd觉得,即使这样明天也能恢复出一个排队顺序,使得任意一个人的两个方向中至少有一个方向上的比他高的人数和他记住的数字相同。可惜n比较大,显然需要写个程序来解决,nodgd很忙,写程序这种事情就交给你了。
输入格式
第一行输入一个整数n,表示指令的条数。(n<=100000,身高在整型范围)
接下来n行,每行两个整数ai,bi,表示一个人的身高和她记住的数字,保证身高互不相同。
输出格式
输出一行,这个队列里从前到后的每个人的身高。如果有多个答案满足题意,输出字典序最小。如果不存在满足题意的排列,输出“impossible”
输入样例
4
4 1
3 1
6 0
2 0
输出样例
2 4 3 6
提示
在所给出的答案队列中,第一个人身高为2,前面有0个人比他高,所以他是输入的第4个人;第二个人身高为4,右边有1个人比他高,所以他是输入的第1个人;第三个人身高为3,右边有1个人比他高,所以他是输入的第2个人;第四个人身高为6,左边有0个人比他高,所以他是输入的第3个人。
显然,如果排列为“6 3 4 2”也是满足题意的,但是字典序不是最小的
分析
这个题的思路难以表述,可我还是要来强行口胡一波
考虑从小到大进行插入,因为这样可以在插入时贪心尽量控制字典序最小,即把当前的人尽量往前放。
我们先预处理出对于每个人,有多少个人比她高,如果比她高的人的个数小于她所记住的数则无解。
然后能够算出她前面最少有多少个人比她高,假设为k个
那么她插入时,因为是从小到大插入的,所以前面就应该预留k个空位给比她高的人,她就在第k+1个空位处
这样就既可以保证有解,还可以保证字典序最小。
但如果存在相同高度的人时,可能前面应该预留不止k个空格,因为后面的插入可能会占用某个空格却不作贡献
即如果两个人高度相同,k较大的人先插入,k较小的后插入,k较小的人就会破坏k较大的人所预留出来的空位
如图,1号的高度与2号相等,1号的k=5,2号的k=2

1号插入时给比她高的人留了k个空位
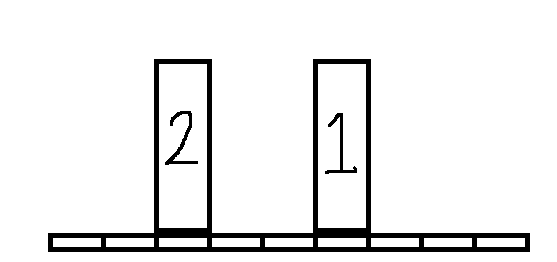
但是当2号插入时会占用一个空位却不作出贡献
而先插入2号再插入1号就不存在这样的问题
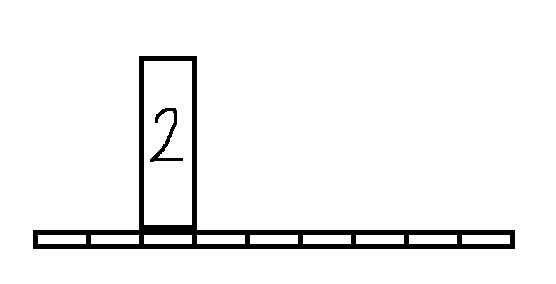

所以,遇到相同高度时就按k从小到大排序后在插入即可。
那么问题来了,我们如何来实现呢?
我们可以用树状数组来维护
每一个空格的值为1,这样某个位置的前缀和就是这个位置及之前共有多少个空位
显然越往右前缀和是单增的,所以可以二分确定第k个空位的位置
在插入一个人的时候,先二分出第k+1空位的位置,记录答案,然后在树状数组中修改这个位置的值,再去插入下一个人
复杂度为O(nlog^2n)。好像树状数组还有nlogn的做法,但我想咕了。
代码
#include<cstdio>
#include<algorithm>
using namespace std;
int n,vis[100005],bit[100005],ans[100005];
struct node{int h,id;}st[100005];
void add(int x,int k){for(;x<=n;x+=(x&-x))bit[x]+=k;}
bool cmp(node a,node b){return a.h==b.h?a.id<b.id:a.h<b.h;}
int que(int x){int s=0;for(;x;x-=(x&-x))s+=bit[x];return s;}
int main()
{
scanf("%d",&n);for(int i=1;i<=n;i++)scanf("%d%d",&st[i].h,&st[i].id);
sort(st+1,st+1+n,cmp);int flag=0;
for(int i=1,l,r;i<=n;add(i,1),i++)
{
l=r=i;while(st[i].h==st[i+1].h)i++,r++;
for(int j=l;j<=r;j++)flag|=(st[j].id=min(n-r-st[j].id,st[j].id))<0;
}
if(flag)return puts("impossible"),0;sort(st+1,st+1+n,cmp);
for(int i=1;i<=n;i++)
{
int l=1,r=n,mid,pos;
while(l<=r)
{
mid=(l+r)>>1;
if(que(mid)>=st[i].id+1)r=mid-1,pos=mid;
else l=mid+1;
}
add(pos,-1);
ans[pos]=st[i].h;
}
for(int i=1;i<=n;i++)printf("%d%c",ans[i],i==n?'\n':' ');
}

