树——倍增LCA
与正文无瓜的前言
身为一个高一才开始学的OIER,现在才开始恶补模板,感觉今年就要退役了。
不想刷题了滚过来写写博客<-------极端危险的思想。
引入
LCA(Lowest Common Ancestors),即最近公共祖先,听名字就知道这是与树上两个节点有关的东西。
它的定义就是两个点最近的公共祖先(废话),同时它也是树上一个节点到另一个节点的最短路中经过的深度最小的点。
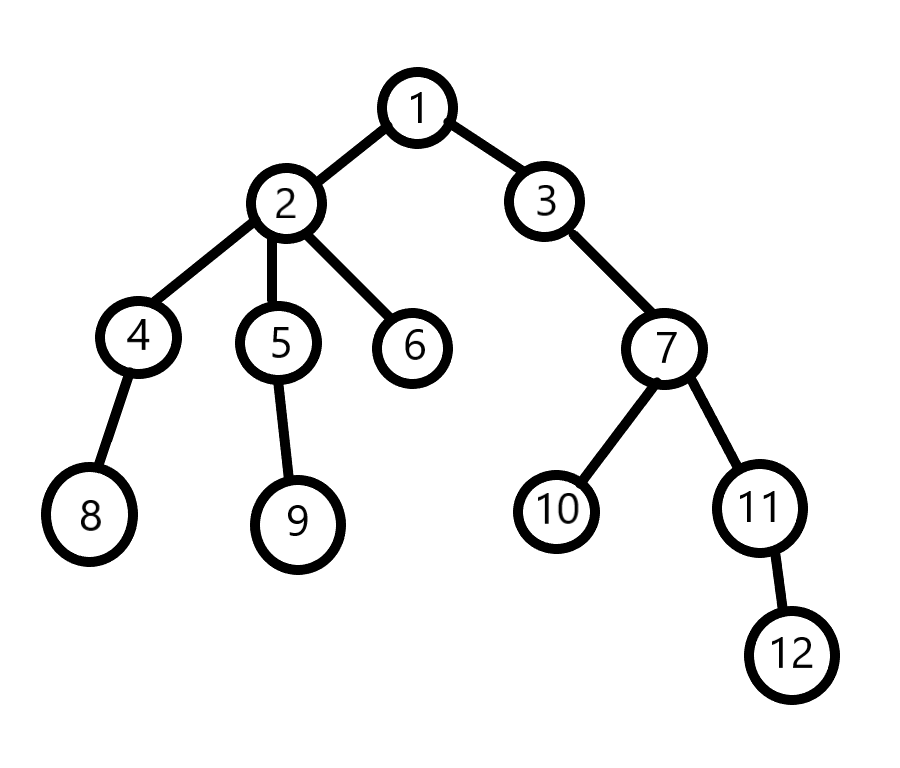
如图,2就是8与9的最近公共祖先,7就是10和12的最近公共祖先。
那么LCA有什么用呢?
举个例子,我们可以利用LCA在O(1)的时间复杂度内求出树上两点u,v的最短距离。这里用dep表示节点的深度。
dis(u,v)=dep(u)+dep(v)-2*dep(LCA(u,v));
所以能快速求出LCA就可以快速求出两点间的距离。当然LCA还有其它作用,这里就不再赘述了(其实我并不知道)。
正文
我们来想一下一般的LCA求法。
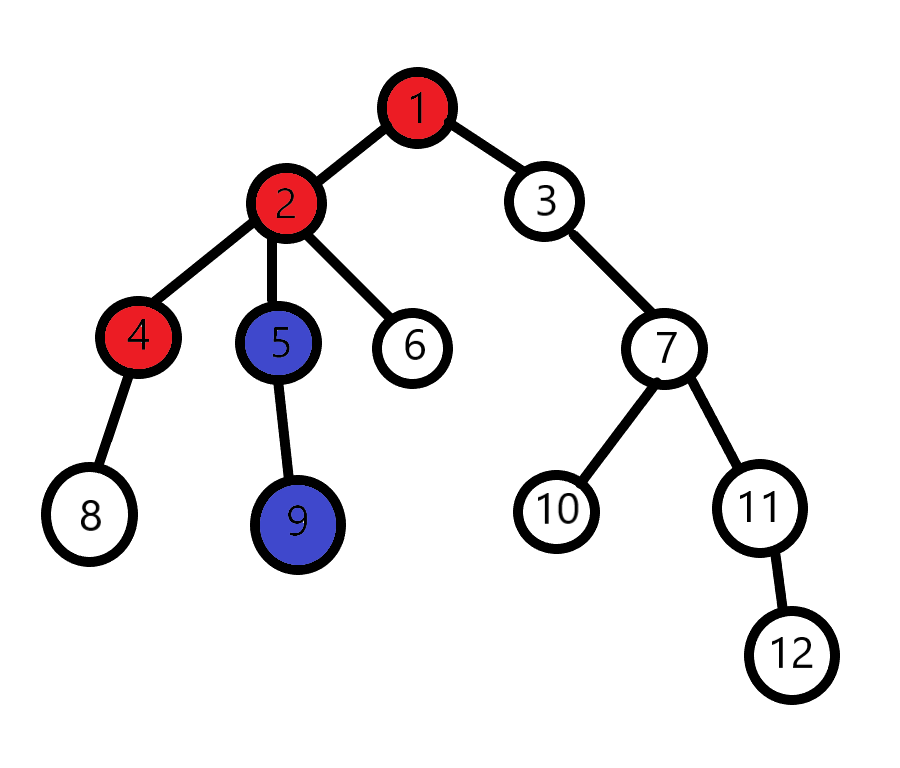
对于任意两个节点u,v,如果我们一开始让它们同时向上寻找祖先,因为它们深度可能不同,其中深度较低的点就会向上走过头。
就像这样:
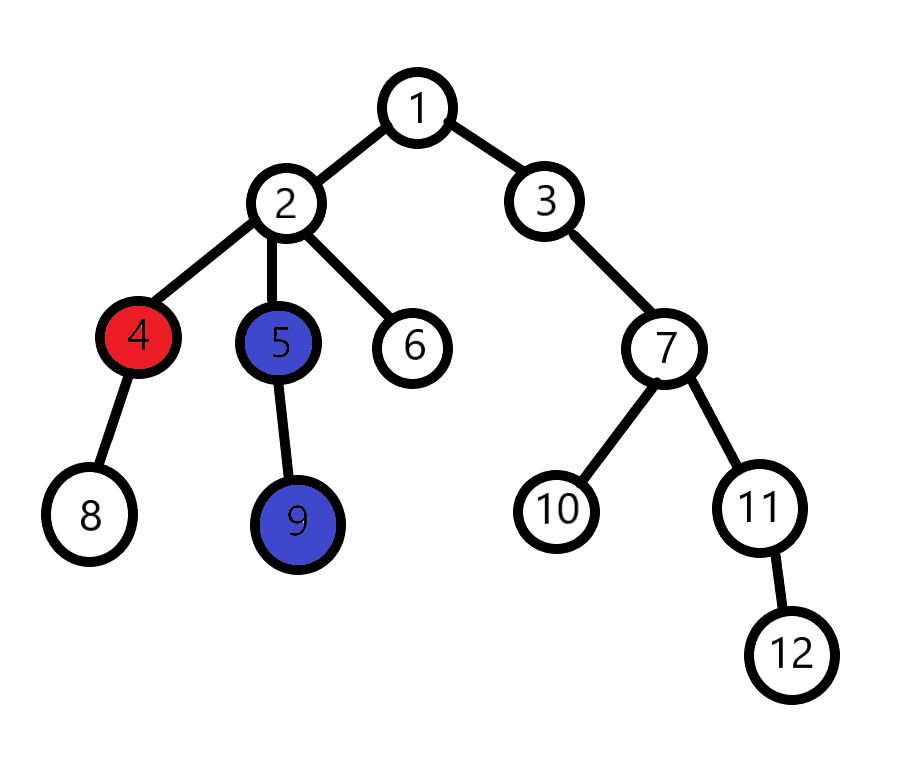
所以我们先让深度较深的点先向上走,走到与另一个点深度相同时,两个点再肩并肩向上走,找到第一个公共祖先为止。

而用倍增求LCA的方法也跟这个差不多,只不过不是一步一步向上走,而是先预处理出每个点向上走2^k步到达的节点,再向上飞。
设fa[i][j]为i节点向上走2^j步到达的节点,那么fa[i][j]可以这么转移:fa[i][j]=fa[ fa[i][j-1] ][j-1]转移过来。
这里介绍两种预处理的方式。
一种是一边遍历树一边处理,代码如下:
void dfs(int x,int f)
{
dep[x]=dep[fa[x][0]=f]+1;
for(int j=1;j<=20;j++)
fa[x][j]=fa[fa[x][j-1]][j-1];
for(int i=info[x];i;i=nex[i])if(v[i]!=f)dfs(v[i],x);
}
另一种是先遍历,然后处理,代码:
1 void dfs(int x,int f)
2 {
3 dep[x]=dep[fa[x][0]=f]+1;
4 for(int i=info[x];i;i=nex[i])if(v[i]!=f)dfs(v[i],x);
5 }
6 void pre()
7 {
8 dfs(1,0);
9 for(int j=1;j<=LOG;j++)for(int i=1;i<=n;i++)
10 fa[i][j]=fa[fa[i][j-1]][j-1];
11 }
预处理完后,我们就可以让深度较深的节点快速的与另一个节点会和,然后比翼双飞

直接给出代码和注解:
int lca(int x,int y)
{
if(dep[x]<dep[y])swap(x,y);
int delta=dep[x]-dep[y];
for(int i=LOG;i>=0;i--)
if(delta&(1<<i))x=fa[x][i];//将delta转化为二进制,再用2^i凑出来
if(x==y)return x;
for(int i=LOG;i>=0;i--)//用2^i凑距离,对于每个2^i只有可能被用一次,从大到小就是为了防止多用。
if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];//如果相等就一起向上飞,会飞到公共祖先,但不是最近的
return fa[x][0];
}

