数据结构——线段树与树状数组

 

写在前面

貌似是我这个菜文鸡第一次写总结。

一咕再咕的我总算滚回来学线段树和树状数组啦，然而此时身边大佬早已过了紫荆花之恋。

看了一堆网上的文章和高二大佬们留下来的书，写下来方便以后复习。

引入

给出n个数，再给出m次操作，操作包含

1.求出区间[l,r]的最大值（区间查询）

2.求出第k个数的值（单点查询）

3.给区间[l,r]增加一个值x（区间修改）

4.给第k个数加上一个值x（单点修改）

如果n*m«100000000，对于每次询问就可以O(n)暴力出奇迹。

但如果n*m≥100000000,想打暴力的同学恐怕就要自闭分离了。

这个时候，就需要数据结构来维护我们得到的信息。

（问：什么是数据结构？众大佬：就是在考场上没人打得出来的毒瘤。）

我们来看看两个相对简单的数据结构—线段树和树状数组

正文

线段树

    这里是度娘给出的定义“线段树是一种二叉索引树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点”。

    显然，大家看完这句话后应该都是懵逼的。线段树，顾名思义，就是线段（区间）的树。而这棵树一般是二叉树（如图）。

   

如果把字母换成一段线段（区间）[l,r]，节点左右儿子为区间的中点隔开的左右子区间[l,mid]和[mid+1,r]，这棵二叉树就是线段树。Just like this。

或者当数字不是这么好看的时候就会变成这样：

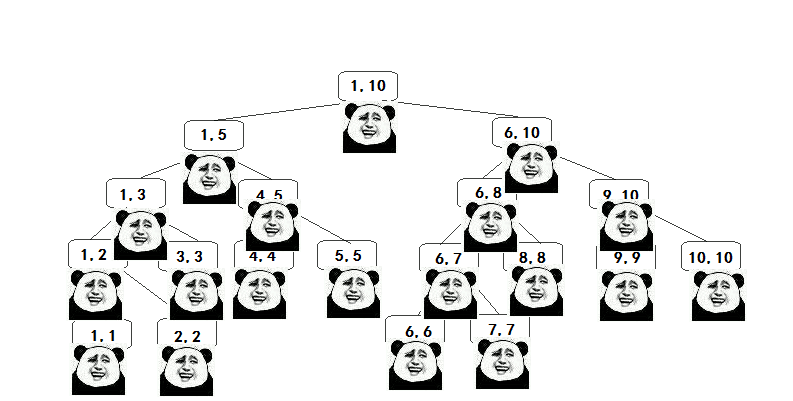
 接下来我们需要给每个区间编号，再通过编号用数组来维护相应区间的信息（如该区间的儿子的编号，区间和，区间最大值等）。

编号的方式跟二叉树的一样，根节点(即代表整段区间的节点)的编号为1，那么编号为i的节点的左儿子编号为2*i，右节点的编号为2*i+1。如何证明这些编号不会重复呢？把它们转化成二进制就很好想了。乘2代表左移（向下一层），不加1代表左儿子，加1代表右儿子，这样编号就可以反应一段区间在线段树的第几层的哪个位置，而位置是不会重复的，所以编号也不会重复。

到这里，我们就可以写出线段树建树的代码了，只需将一个节点的两个儿子找到。当然，建树过程中也可以加入初始值。

 

void build(int l,int r,int id)
{
    if(l==r)return;/到达叶子节点，也可以在这里加入初始值/
    build(l,mid,id*2);build(mid+1,r,id*2+1);
    ch[id][0]=id*2;ch[id][1]=id*2+1;/记录儿子编号/
} 

接下来，我们就来看如何维护一段区间的信息。

在给每个区间编号后就可以用编号代表区间，用数组来维护区间的信息。

线段树能维护的区间信息必须是可以通过子区间的信息求出来的，比如区间最大（最小）值，区间和，这些都可以通过子区间的信息来维护。

对于单点修改，单点查询，每次维护时都要从线段树的根节点向下访问到叶子节点，进行修改和查询，再依次向上更新区间信息，所以每次的时间复杂度为logn。

对于区间查询，每次访问的复杂度类似，也是logn，我不会证明。

我们可以直接去访问

但是，对于区间修改，如果一个个向下访问，时间复杂度貌似是nlogn，这似乎比只用数组复杂度还要高。

于是，一个强大的东西诞生了———懒标记。再次顾名思义，这种标记很懒。只要能简单办事，就真的只用最简单的方法。

 

当一个区间修改的范围大于当前区间的范围，我们可以用一个变量存下，或者说标记一下这段区间被修改的值（比如增加多少值，或者增加多少倍），这个标记就被称作懒标记。当需要访问或修改这个区间的子区间时，再将这个标记下传给左右子区间（可以先更新再标记再下传，或者先标记再下传再更新）。

所以修改和查询就该写成（以加法为例）：

 

void pushdown(int l,int r,int id)
{
    laz[ch[id][0]]+=laz[id];
    laz[ch[id][1]]+=laz[id];
    sum[id]+=(r-l+1)*laz[id];
    laz[id]=0;
}
void add(int l1,int r1,int k,int l,int r,int id)
{
    
    if(r1<l||r<l1)return;/如果修改范围不包括此区间则退出，这是一种比较偷懒的写法/
    if(l1<=l&&r<=r1){if(l==r)sum[id]+=k;else laz[id]+=k;return;}/完全覆盖则打上懒标记，如果是叶子节点就直接修改值/
    if(laz[id])pushdown(l,r,id);/懒标记下传/
    if(l!=r)add(l1,r1,k,l,mid,ch[id][0]),add(l1,r1,k,mid+1,r,ch[id][1]);
    sum[id]=sum[ch[id][0]]+sum[ch[id][1]]+(mid-l+1)*laz[ch[id][0]]+(r-mid-1+1)*laz[ch[id][1]];/更新值/
}
long long que(int l1,int r1,int l,int r,int id)
{
    if(r1<l||r<l1)return 0;
    if(l1<=l&&r<=r1)return sum[id]+(r-l+1)*laz[id];
    if(laz[id])pushdown(l,r,id);
    return que(l1,r1,l,mid,ch[id][0])+que(l1,r1,mid+1,r,ch[id][1]);
}

 树状数组 

如果只想查询区间和，但线段树写起来很困难，怎么办？

我们来观察一些线段树。

 

 

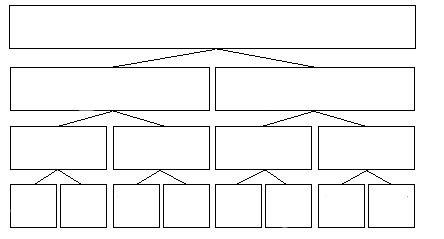
 由于我们只会查询区间和，而一个区间的和等于它左右儿子区间和，所以，一个区间的和，它左儿子区间的和，右儿子区间的和，这三个量是知二求三的。

所以我们把右儿子都标记起来，像这样

 

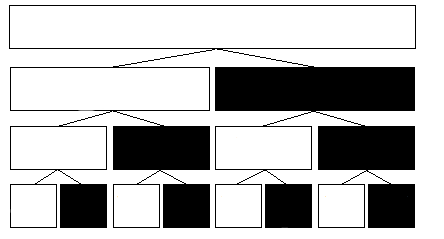
再把它们都去掉

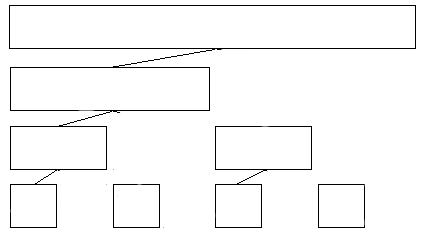
我们就可以只维护这些区间的和，当需要右儿子的和时，用父亲的和减去左儿子的和就可以了（当然，实际操作并不是这样，这样只是方便理解为什么只维护这些区间就可以求出区间和）。

 

 

这时，我们就很容易发现每个区间的右端点都不会重复，我们就可以用右端点的下标来表示这段区间，用数组维护区间和了。

这就是树状数组。

每个下标维护前缀和的长度是2^(它们转化成二进制后末位0的个数)。

比如

7在二进制下是111，那它就维护以它为右端点的长度为2^0=1的区间（即[7,7]）。

而6在二进制下是110，那它就维护以它为右端点的长度为2^1=2的区间（即[5,6]）。

而每个区间的父亲的号码为 它们自己本身 加上 2^(它们转化成二进制后末位0的个数)<---就是加上它们自己所维护区间的长度。

很容易想到单点修改，区间查询的方法

就是将所有包含那个点的区间的和加上变化的值。

即从以那个点的位置为下标代表的区间开始，依次更新，从儿子到父亲。

这是更新时需更新区间的图示

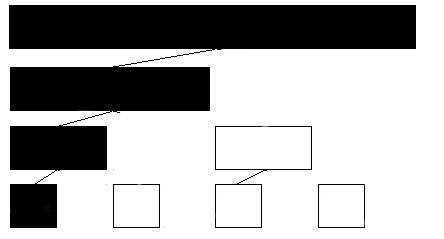
这是维护的代码

 

void add(int i,int x){for(;i<=n;i+=i&-i)bit[i]+=x;}//让第i个位置的值加上x

 查询时，我们利用前缀和思想，sum（i，j）=sum（1，j）-sum（1，i）。

查询sum（1，i）时，将以i为下标代表的区间的和，加上它父亲的左边的区间的和，再加上它父亲左边区间的父亲左边的区间的和。。。。。。

还是给图示吧

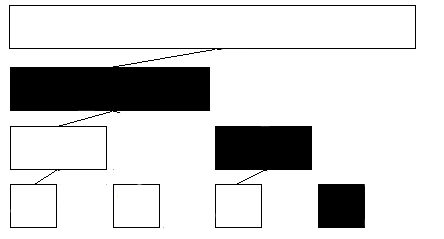
每个区间的父亲左边区间的下标为 它们自己本身的下标 减去 2^(它们转化成二进制后末位0的个数)<---就是加上它们自己所维护区间的长度

然后又是代码

 

long long sum(int i){long long s=0;for(;i;i-=i&-i)s+=bit[i];return s;}//求sum（1，i）

 

 

 

 如果我们换储存思路，用sum（1，i）来表示第i个数的值，那么就可以做到区间修改，单点查询。

修改时把区间左右端点的值减去，加上相应的值就完事了。

单点查询时直接查sum（1，i）就好了；

 

最后，给出模板题的代码。

洛谷【模板】线段树1

#include<cstdio>
#include<algorithm>
#define mid (l+r)/2
#define maxn 1000005
using namespace std;
int n,m,ch[maxn][2];
long long sum[maxn],laz[maxn];
void pushdown(int l,int r,int id)
{
    laz[ch[id][0]]+=laz[id];
    laz[ch[id][1]]+=laz[id];
    sum[id]+=(r-l+1)*laz[id];
    laz[id]=0;
}
void build(int l,int r,int id)
{
    if(l==r)return;
    build(l,mid,id*2);build(mid+1,r,id*2+1);
    ch[id][0]=id*2;ch[id][1]=id*2+1;
}
void add(int l1,int r1,int k,int l,int r,int id)
{
    
    if(r1<l||r<l1)return;
    if(l1<=l&&r<=r1){laz[id]+=k;return;}
    add(l1,r1,k,l,mid,ch[id][0]);
    add(l1,r1,k,mid+1,r,ch[id][1]);
    sum[id]=sum[ch[id][0]]+sum[ch[id][1]]+(mid-l+1)*laz[ch[id][0]]+(r-mid-1+1)*laz[ch[id][1]];
}
long long que(int l1,int r1,int l,int r,int id)
{
    if(r1<l||r<l1)return 0;
    if(l1<=l&&r<=r1)return sum[id]+(r-l+1)*laz[id];
    if(laz[id])pushdown(l,r,id);
    return que(l1,r1,l,mid,ch[id][0])+que(l1,r1,mid+1,r,ch[id][1]);
}
int main()
{
    scanf("%d%d",&n,&m);build(1,n,1);
    for(int i=1,a;i<=n;i++)scanf("%d",&a),add(i,i,a,1,n,1);
    for(int i=1,ord,l,r,k;i<=m;i++)
    {
        scanf("%d%d%d",&ord,&l,&r);
        if(ord==1){scanf("%d",&k),add(l,r,k,1,n,1);}
        if(ord==2)printf("%lld\n",que(l,r,1,n,1));
    }
}

洛谷【模板】线段树2

#include<cstdio>
#define mid (l+r)/2
#define lc ch[id][0]
#define rc ch[id][1]
#define maxn 400005
int n,m,p,ori[maxn],ch[maxn][2];
long long laz1[maxn],laz2[maxn],sum[maxn];
void pushdown(int l,int r,int id)
{
    sum[id]=(sum[id]*laz1[id]+(r-l+1)*laz2[id])%p;
    laz1[lc]=(laz1[lc]*laz1[id])%p;laz1[rc]=(laz1[rc]*laz1[id])%p;
    laz2[lc]=(laz2[lc]*laz1[id]%p+laz2[id])%p;laz2[rc]=(laz2[rc]*laz1[id]%p+laz2[id])%p;
    laz1[id]=1;laz2[id]=0;
}
void pushup(int l,int r,int id)
{sum[id]=((sum[lc]*laz1[lc])%p+(sum[rc]*laz1[rc])%p+(mid-l+1)*laz2[lc]%p+(r-mid-1+1)*laz2[rc]%p)%p;}
void build(int l,int r,int id)
{
    if(l==r){sum[id]=ori[l]%p;return;}
    build(l,mid,lc=id*2);build(mid+1,r,rc=id*2+1);pushup(l,r,id);
}
void fix(int l1,int r1,int k,int l,int r,int id,int ord)
{
    if(r1<l||r<l1)return;
    if(l1<=l&&r<=r1)
    {
        if(ord==1)laz1[id]=(laz1[id]*k)%p,laz2[id]=(laz2[id]*k)%p;
        if(ord==2)laz2[id]=(laz2[id]+k)%p;return;
    }
    if(l==r)return;pushdown(l,r,id);fix(l1,r1,k,l,mid,lc,ord);fix(l1,r1,k,mid+1,r,rc,ord);pushup(l,r,id);
}
long long que(int l1,int r1,int l,int r,int id)
{
    if(r1<l||r<l1)return 0;
    if(l1<=l&&r<=r1){return (sum[id]*laz1[id]%p+(r-l+1)*laz2[id]%p)%p;}
    pushdown(l,r,id);
    return que(l1,r1,l,mid,lc)%p+que(l1,r1,mid+1,r,rc)%p;
}
int main()
{
    for(int i=0;i<maxn;i++)laz1[i]=1;
    scanf("%d%d%d",&n,&m,&p);
    for(int i=1;i<=n;i++)scanf("%d",&ori[i]);
    build(1,n,1);
    for(int i=1,ord,l,r,k;i<=m;i++)
    {
        scanf("%d%d%d",&ord,&l,&r);
        if(ord==1){scanf("%d",&k);fix(l,r,k%p,1,n,1,ord);}
        if(ord==2){scanf("%d",&k);fix(l,r,k%p,1,n,1,ord);}
        if(ord==3)printf("%lld\n",que(l,r,1,n,1)%p);
    }
    return 0;
}

洛谷【模板】树状数组1

#include<cstdio>
int n,m,ord,x,y;
long long bit[500005];
void add(int i,int x){for(;i<=n;i+=i&-i)bit[i]+=x;}
long long sum(int i){long long s=0;for(;i;i-=i&-i)s+=bit[i];return s;}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1,a;i<=n;i++)
        scanf("%d",&a),add(i,a);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&ord,&x,&y);
        if(ord==1)add(x,y);
        if(ord==2)printf("%lld\n",sum(y)-sum(x-1));    
    }
}

洛谷【模板】树状数组2

#include<cstdio>
int n,m,ord,x,y,k;
long long bit[500005];
void add(int i,int x){for(;i<=n;i+=i&-i)bit[i]+=x;}
long long sum(int i){long long s=0;for(;i;i-=i&-i)s+=bit[i];return s;}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1,a;i<=n;i++)
        scanf("%d",&a),add(i,a),add(i+1,-a);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&ord,&x);
        if(ord==1)scanf("%d%d",&y,&k),add(x,k),add(y+1,-k);
        if(ord==2)printf("%lld\n",sum(x));    
    }
}