浅谈带权二分或者斜率凸优化
APOI讲了这个东西,还有THU命题的《九省·林克卡特树》,感觉好像很热点的样子。
带权二分是一类对DP的优化,对于某些最优化问题的(2d/yd)DP,通过这种优化,其效率可以达到简化后的(1d/yd)DP的效率乘一个log
((xd/yd)DP是指状态数为n^x级且每种状态的转移数为$n^y$级的DP,这个形式下的DP的最好效率是$n^{x+y}$的)
有这么一个(2d/yd)DP:
——对于某状态二元组(i,j),有最优值f[i][j];
——每个f[i][j]的得出,都需要比较$n^y$个其他的状态二元组,从中挑出一个可以使f[i][j]更优的状态作为前驱来进行转移;
——需要某一个f[n][m]的结果(因为n和m同级,所以可以认为状态数为$n^2$级)。
考虑优化这个(2d/yd)DP,也就是把它降为一个其他的(x'd/y'd)DP使得x'+y'<2+y
考虑使y减小——
由于在此类DP中,每一个状态的得出,最终只需要从所有备选的前驱中挑一个来进行转移,
于是在最理想的情况(也就是经过各种神奇优化之后),我们可以不经过比较一步找到每个状态的前驱
这样就是一个(2d/0d)的DP了,效率$O(n^2)$,
对于决策过程的优化就到此为止了,这一部分并不是本文的重点,所以可以看出,他被一笔带过了。
现在我们考虑优化状态数,也就是把2d变成1d——
考虑有一个(2d/yd)DP,我们要得到的是状态(n,m)的最值f[n][m]
如果这个DP没有第二位限制的话是一个非常好搞的1dDP(状态为x时,其答案f'[x]为原来f[x][i]中i枚举所有值时的最优值,由于DP状态的精确性有所下降,所以一般情况下f'的DP的确可以是一个(1d/y'd)DP,而且y'<=y,也就是一个比之前更好搞的DP)
那我们尽量希望把第二位消掉,以优化状态数
设有函数F满足F(i)=f[n][i];
F在整点处的最值,也是对于所有i而言f[n][i]的最值;
那么设这个值为f'[n],可以发现f'[n]就是我们上文中所说的消去第二位限制后出现的那个很好搞的DP
然而,这样得到的f'[n]=f[n][x],却并不能保证x=m。
考虑给F搭配另一个函数G以得到函数H,使得H(x)=F(x)+G(x)
且H(x)在x=m时取得整点处的最值;
这样的话,设这个最值为h'[n],如果h'[n]也恰好是个很好搞的(1d/y''d)DP(这需要G十分恰当),那么h'[n]就可以是我们优化状态数的产物。而最终的答案就是h'[n]-G(m)了
带权二分(斜率凸优化)就是上述讨论的一个简单易行而应用广泛的特例。
比如有f[a][b]=max(枚举c<b){f[a-1][c]+val[c+1,b]},
我们试图消去状态表示中的第一位a,他代表转移次数,
由之前的定义有$F_{max}$=f'[b]=max(枚举i){f[i][b]}
可以发现f'[x]是一个很好搞的DP——
f'[b]=max(枚举c<b){f'[c]+val[c+1,b]}
如果F的曲线满足如下图的凸性:

比如F(x)是下图这样的曲线

那么只要H(x)是F(x)搭配不同斜率的正比例函数G(x)(即H(x)=F(x)+K*x,其中G(x)=K*x),随着K的调动,就可以使不同的x变成H(x)取到最值的地方
而且h'[x]也是一个很好搞的DP——
当G的斜率为K时,h'[b]=max(枚举c){h'[c]+val[c+1,b]+K}
(每转移一次就相当于原来的f中被隐去的维度其数值+1,这意味着G的自变量+1,此时G对h'多贡献了K)
于是剩下的问题就是如何找到一个合适的K,使得H的最优值h'[n]在m处取得了
因为只要K合适,那么答案就是f[n][m]=h'[n]-m*K,而h'是一个很好搞的DP,于是此类题目就结了。
我们发现由于F函数曲线的凸性,当K逐渐减小时,H的最值取得的位置逐渐右移,
这意味着K可以二分取得:
每次二分一个K’,DP计算当前的h'[n],并计算当前h'[n]=H(x)的这个x是那一个x
如果这个x>m就blabla
如果这个x<m就blabla
这样最后会得到了一个合适的K,并同时也就得到问题的答案了。
而对于F的曲线满足如下图凸性的情况:
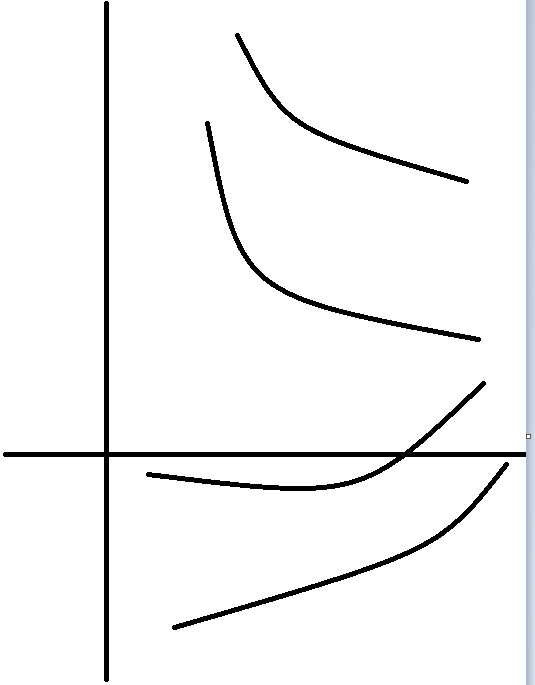
我们可以用同样的方法,搭配不同斜率的正比例函数G(x)使得H(x)的min值在不同的x处取得。
方法之前的类似。
总结:
对于f[n][m]
如果f[n][m]求解max值
且设F(x)=f[n][x],有F(x)是随x增加,斜率递减的函数
那么我们可以通过斜率凸优化解决这个问题
如果f[n][m]求解min值
且设F(x)=f[n][x],有F(x)是随x增加,斜率增的函数
那么我们可以通过斜率凸优化解决这个问题
例子:
有如下DP方程——
$$f_{[i][j]}=MIN_{k∈[0,j-1]}f_{[i-1][k]}+(sum_{l=k+1}^{j}a[l])^2$$
$$且对于所有i>j,有f_{[i][j]}=INF$$
其中a[x]为输入数据
求解$f_{[m][n]}$
可以看出$f_{[m][n]}$为把n个数分成m段,求每段和的平方的和。
设$F(x)=f{[x][n]}$可以证明F(x)是一个随x增加,斜率增的函数。
如果没有m段的限制的话
有$f'_{[j]}=MIN_{k∈[0,j-1]}f_{[k]}+(sum_{l=k+1}^{j}a[l])^2$
通过预处理前缀和以及一些斜率优化技巧,这个方程可以做到O(n)
如果我们给每次划分搭配一个费用K的话
就有$h'_{[j]}=MIN_{k∈[0,j-1]}h_{[k]}+(sum_{l=k+1}^{j}a[l])^2+K$
同样可以斜率优化做到O(n),
这样,我们二分K,判定此时$h'_{[n]}$对应的划分次数与m的关系,从而找的一个合适的K,进而找的问题的答案。
最终效率为O(nlogV)




