从零开始认识堆排序
一、什么是堆?
维基百科的解释是:堆是一种特别的树状数据结构,它需要满足任意的子节点必须都大于等于(最大堆)或者小于等于(最小堆)其父节点。
二、堆排序
堆排序是通过二叉堆数据结构实现,二叉堆满足以下两个特性:
1、满足堆的基本特性
2、完全二叉树,除了最底层外,其它层都已填充满,且是从左到右填充。
二叉堆的高度即为根节点到叶子节点的最长简单路径长度,即为θ(lgn)。
二叉堆上的操作时间复杂度为O(lgn)。
1、二叉堆中的元素个数
根据二叉堆的特性2,我们知道高度为h的二叉堆重元素个数如下:
根节点为1
第一层为2=21
第二层为4=22
...
第h-1层为2h-1
第h层元素个数范围为[1,2h]
最底层之外的元素个数和为1+2+22+...+2h-1=(1-2h-1)/(1-2)=2h-1
高度为h的二叉堆元素个数范围:[2h-1 + 1,2h-1+2h]=[2h,2h+1-1]
以高度为3的最大堆为例:
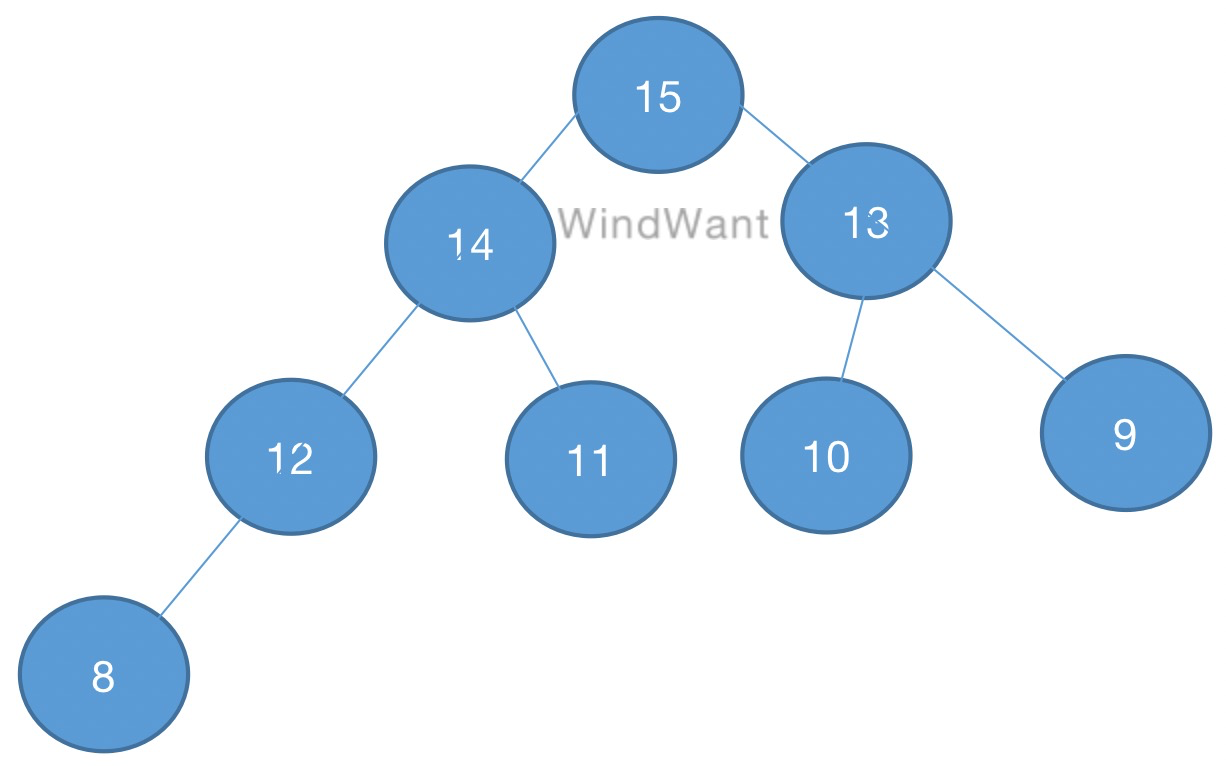
图1

图2
2、二叉堆的高度
由二.1推导,我们知道高度为h的二叉堆的元素个数n满足:
2h ≦ n ≦ 2h+1-1
=>
2h ≦ 2lgn ≦ 2h+1-1
=>
h ≦ lgn < h+1
由此可得,含有n个元素的二叉堆的高度为θ(lgn)
3、使用数组表示堆存储
节点下标 i,则父节点下标为 i/2,左子节点下标为 2i,右子节点下标 2i + 1。
以图1最大堆为例:
从根节点开始,根节点下标 1。
第一层节点下标:2、3
第二层节点下标:4、5、6、7
第三层节点下标:8

图3
数组形式:
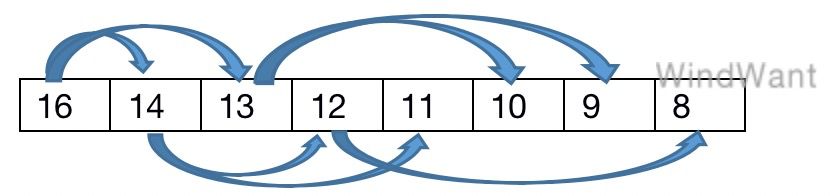
图4
具体到特定的编程语言,数组以0开始下标的,推导:
对于节点 i,则其父节点为 (i - 1)/2,左子节点下标为 2i + 1,右子节点下标 2i + 2。
4、堆的叶子节点
对于有n个元素的二叉堆,最后一个元素的下标为为n,根据二叉堆的性质,其父节点下标为n/2,因为每一层是由左向右进行构建,所以其父节点也是倒数第二层的最后一个节点,所以,其后的节点都为最底层节点,为叶子节点,下标为n/2 + 1、n/2 + 2... n。
具体到特定的编程语言,数组以0开始下标的,推到:
叶子节点下标为(n-1)/2 + 1、(n-1)/2 + 2... n。
5、堆维护
所谓堆维护,即保持堆的基本特性,以最大堆为例:给定某个节点,维护使得以其为根节点的子堆为满足子节点都小于等于父节点。
如下,给定堆构建数组,及特定元素下标i:
public static void maxHeapify(int[] arr, int i) { int size = arr.length; //堆大小 int maxIndex = i; //记录当前节点及其子节点的最大值节点索引 int left = 2 * i + 1; //左子节点索引 int right = 2 * i + 2; //右子节点索引 //对比节点及其左子节点 if (left < size && arr[left] > arr[maxIndex]) { maxIndex = left; } //对比节点及其右子节点 if (right < size && arr[right] > arr[maxIndex]) { maxIndex = right; } //不满足最大堆性质,则进行下沉节点i,递归处理 if (maxIndex != i) { int tmp = arr[i]; arr[i] = arr[maxIndex]; arr[maxIndex] = tmp; maxHeapify(arr, maxIndex); } }
如下图,堆中元素9的维护过程:
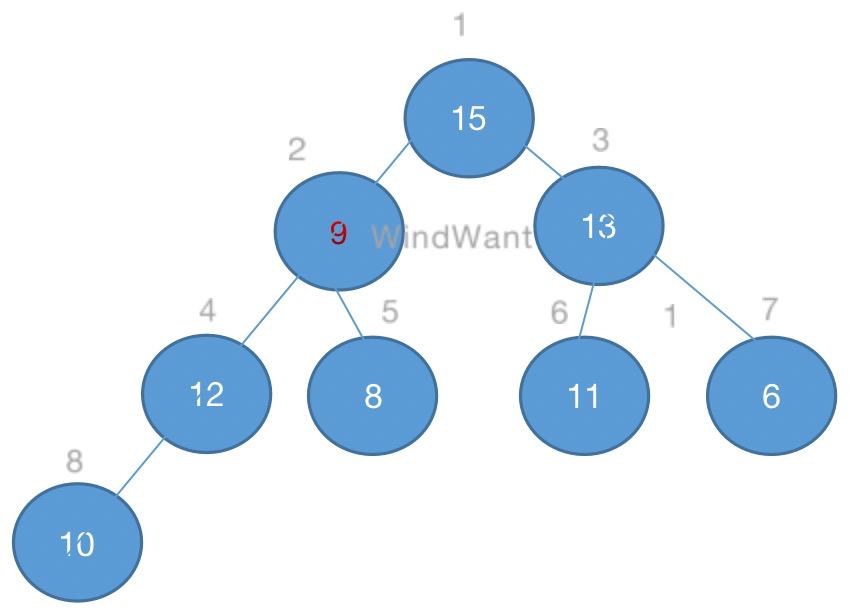
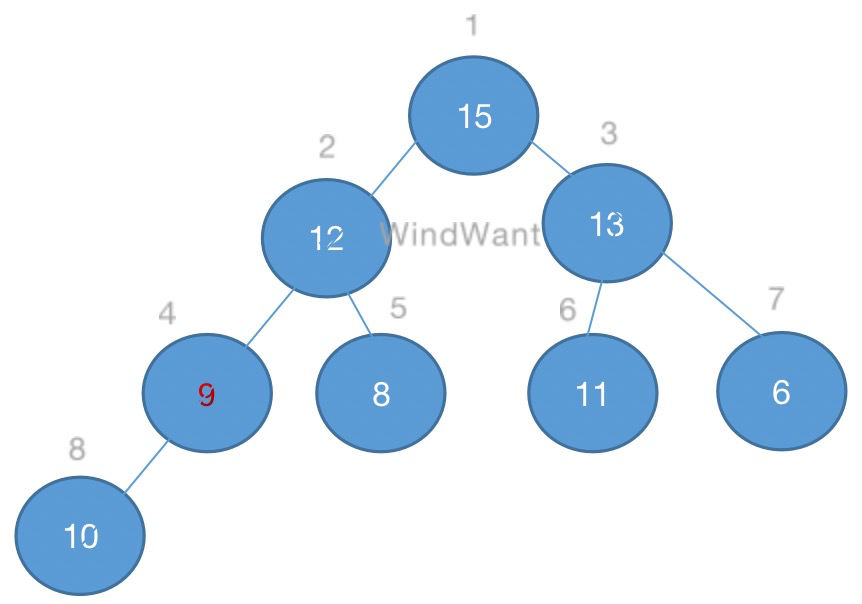
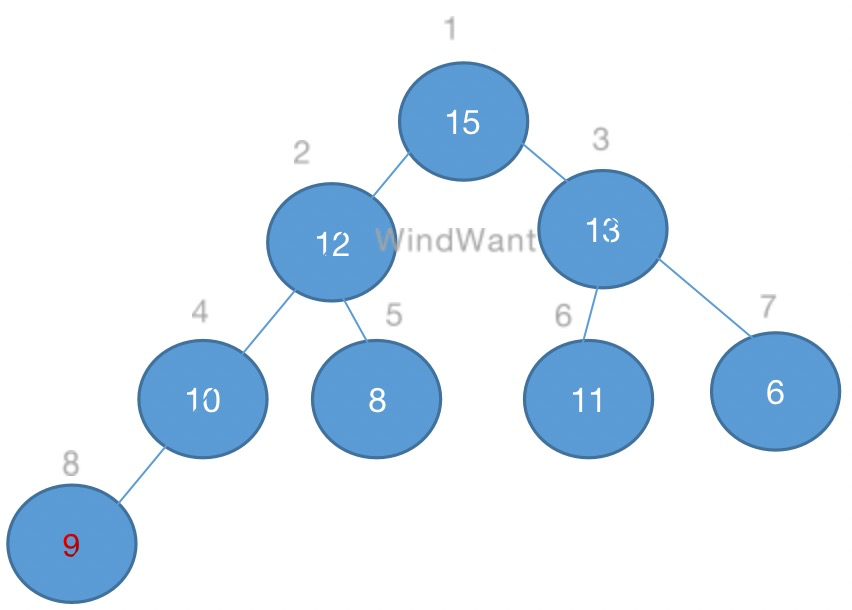
图5
堆维护过程的时间复杂度:O(lgn)。
6、构建堆
根据二.4我们可以得到所有叶子节点的下标。我们可以使用二.5中的堆维护过程,对所堆中所有的非叶子节点执行堆维护操作进行堆的构建。
public static void buildHeap(int[] arr) { for (int i = (arr.length - 1) / 2; i >= 0; i--) { maxHeapify(arr, i); } }
以数组 {27,17,3,16,13,10,1,5,7,12,4,8,9,0} 为例进行堆构建,结果为:{27,17,10,16,13,9,1,5,7,12,4,8,3,0}

图6
构建最大堆的时间复杂度为O(n)。
7、堆排序
首先执行最大堆构建,当前堆中最大值会上升到根节点,也就是堆数组的首节点。
我们可以通过交换首尾节点,使得最大值转移至尾部,然后对除尾部元素外的堆数组执行根元素堆维护,上浮堆最大值。
然后,将最大值交换至数组尾部倒数第二个元素位置,重新执行剩余堆数组的根元素堆维护,依次类推,直至剩余堆数组大小变为2为止。
以二.6中数组为例:{27,17,3,16,13,10,1,5,7,12,4,8,9,0}
第一次执行:
{27,17,10,16,13,9,1,5,7,12,4,8,3,0},max:27
第二次执行:
{17,16,10,7,13,9,1,5,0,12,4,8,3},max:17
第三词执行:
{16,13,10,7,12,9,1,5,0,3,4,8},max:16
第四次执行:
{13,12,10,7,8,9,1,5,0,3,4},max:13
第五次执行:
{12,8,10,7,4,9,1,5,0,3},max:12
第六次执行:
{10,8,9,7,4,3,1,5,0},max:10
第七次执行:
{9,8,3,7,4,0,1,5},max:9
第八次执行:
{8,7,3,5,4,0,1},max:8
第九次执行:
{7,5,3,1,4,0},max:7
第十次执行:
{5,4,3,1,0},max:5
第十一次执行:
{4,1,3,0},max:4
第十二次执行:
{3,1,0},max:3
第十三次执行:
{1,0},max:1
改造代码实现:
/** * 最大堆维护 * * @param arr 堆数组 * @param i 维护元素下标 * @param offSet 原址偏移量 */ public static void maxHeapify(int[] arr, int i, int offSet) { int size = arr.length - offSet; //堆大小 int maxIndex = i; //记录当前节点及其子节点的最大值节点索引 int left = 2 * i + 1; //左子节点索引 int right = 2 * i + 2; //右子节点索引 //对比节点及其左子节点 if (left < size && arr[left] > arr[maxIndex]) { maxIndex = left; } //对比节点及其右子节点 if (right < size && arr[right] > arr[maxIndex]) { maxIndex = right; } //不满足最大堆性质,则进行下沉节点i,递归处理 if (maxIndex != i) { int tmp = arr[i]; arr[i] = arr[maxIndex]; arr[maxIndex] = tmp; //因为交换了子节点的值,则以子节点为根节点的子堆特性可能发生变化,需要维护 maxHeapify(arr, maxIndex, offSet); } } /** * 构建最大堆 * * @param arr */ public static void buildHeap(int[] arr) { for (int i = (arr.length - 1) / 2; i >= 0; i--) { maxHeapify(arr, i, 0); } } /** * 交换最大值 * * @param arr 堆数组 * @param maxIndex 最大值元素待交换位置 */ public static void swapMax(int[] arr, int maxIndex) { int tmp = arr[maxIndex]; arr[maxIndex] = arr[0]; arr[0] = tmp; } /** * 堆排序 * * @param arr */ public static void heapSort(int[] arr) { buildHeap(arr); //构建堆 swapMax(arr, arr.length - 1); //交换最大值 for (int i = 0; i < arr.length - 2 ; i++) { maxHeapify(arr, 0, i + 1); //根节点堆维护 offset 偏移元素个数 swapMax(arr, arr.length - 1 - (i + 1)); //交换最大值 } }
堆排序时间复杂度:O(nlgn)
三、附加订阅




