WebGL编程读书笔记

WebGL概述
- WebGL起源
- WebGL程序的结构
WebGL入门
绘制和变换三角形
高级变换与动画基础
- 平移，然后旋转
  - 矩阵变换库：cuon-matrix.js
  - 复合变换
- 动画
  - 请求再次被调用（requestAnimationFrame()）
颜色与纹理
OpenGL ES 着色器语言（GLSL ES）
进入三维世界
光照
层次模型

WebGL概述

WebGL起源

在个人计算机上使用最广泛的两种三维图形渲染技术是 Direct3D 和 OpenGL。Direct3D 是微软 DirectX 技术的一部分，是一套由微软控制的编程接口(API)，主要用在 Windows 平台;而 OpenGL 由于其开放和免费的特性，在多种平台上都有广泛地使用:它可以在 Macintosh 或 Linux 系统的计算机、智能手机、平板电脑、家用游戏机(如PlayStation和 Nintendo)等各种电子设备上使用。Windows对 OpenGL 也提供了良好的支持，开发者也可以用它来代替Direct3D。

OpenGL 最初由 SGI (Silicon Graphics Inc)开发，并在1992 年发布为开源标准。多年以来，OpenGL 发展了数个版本，并对三维图形开发、软件产品开发，甚至电影制作产生了深远的影响。写这本书时，OpenGL 桌面版的最新版本为 4.3。虽然 WebGL 根植于 OpenGL，但它实际上是从 OpenGL 的一个特殊版本 OpenGL ES 中派生出来的，后者专用于嵌入式计算机、智能手机、家用游戏机等设备。OpenGL ES 于 2003 ~ 2004 年被首次提出，并在 2007 年 (ES 2.0) 和 2012年 (ES 3.0) 进行了两次升级，WebGL 是基于 OpenGL ES 2.0 的。这几年，采用 OpenGL ES 技术的电子设备的数量大幅增长，如智能手机 (iPhone 和安卓)、平板电脑、游戏机等。OpenGL ES 成功被这些设备采用的部分原因是，它在添加新特性的同时从 OpenGL 中移除了许多陈旧无用的旧特性，这使它在保持轻量级的同时，仍具有足够的能力来渲染出精美的三维图形。

下图显示了 OpenGL、OpenGL ES 1.1/2.0/3.0和 WebGL 的关系。由于 OpenGL 本身已经从 1.5 发展到了2.0，再到 4.3，所以 OpenGL ES 被标准化为特定版本 OpenGI(OpenGL 1.5 和 OpenGL 2.0) 的子集。

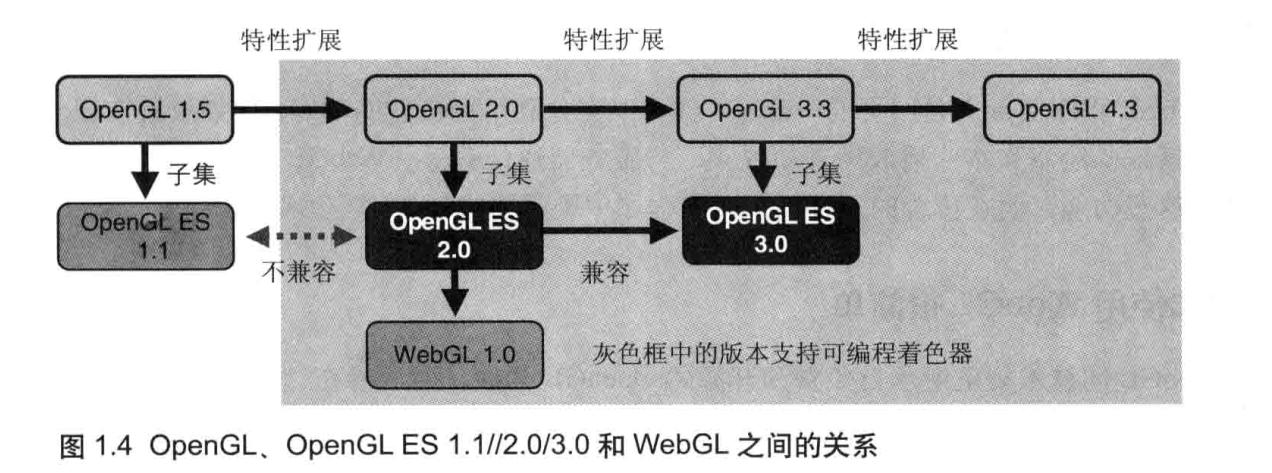
如图所示，从 2.0 版本开始OpenGL 支持了一项非常重要的特性，即可编程着色器方法(programmable shader functions)。该特性被 OpenGL ES 2.0 继承，并成为了WebGL 1.0 标准的核心部分。

着色器方法，或称着色器，使用一种类似于 C 的编程语言实现了精美的视觉效果本书将一步步阐述着色器，帮助你快速掌握 WebGL。编写着色器的语言又称为着色器语言(shading language)，OpenGL ES 2.0 基于 OpenGL 着色器语言(GLSL)，因此后者又被称为 OpenGL ES 着色器语言(GLSL ES)WebGL 基于 OpenGL ES 2.0，也使用 GLSLES 编写着色器。

OpenGL 规范的更新和标准化由 Khronos 组织 (一个非盈利的行业协会,专注于制定发布、推广多种开放标准)负责。2009 年，Khronos 建立了 WebGL 工作小组，开始基于OpenGL ES 着手建立 WebGL 规范，并于 2011 年发布了 WebGL 规范的第1个版本。本书主要基于第1版的 WebGL 规范编写，后续更新目前都是以草案的形式发布，如有需要也可参考。

WebGL程序的结构

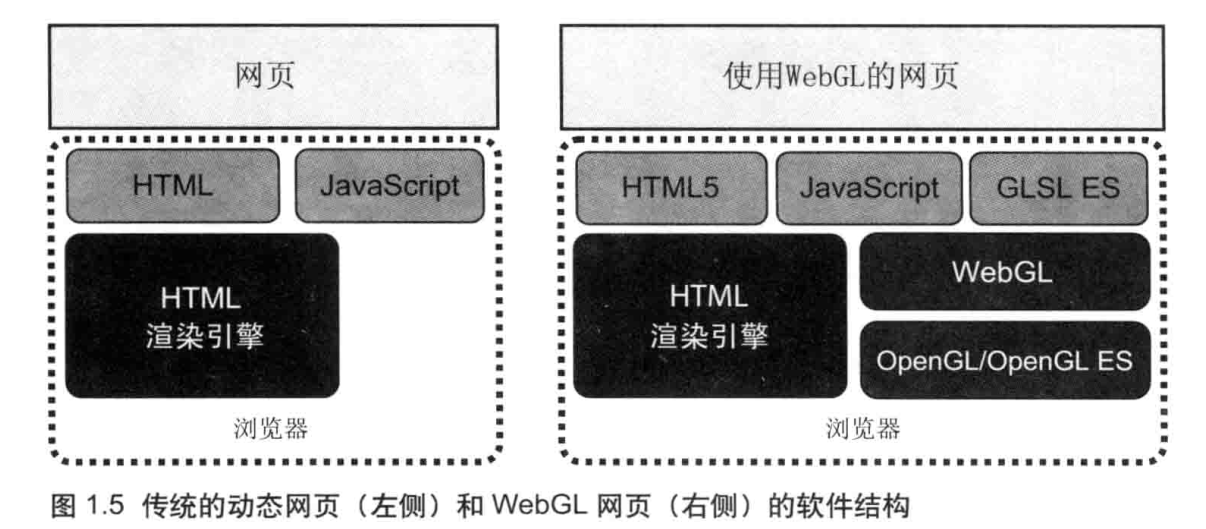
在 HTML 中，动态网页包括 HTML 和 JavaScript 两种语言引人 WebGL 后，还需也就是说，WebGL 页面包含了三种语言:HTML5 (超文要加入着色器语言 GLSL ES(左侧)和使用传统的动态网页本标记语言)、JavaScript，和 GLSL ES.WebGL 的网页 (右侧) 的软件结构。

然而，因为通常 GLSL ES 是 (以字符串的形式)在 JavaScript 中编写的，实际上WebGL 程序也只需用到 HTML 文件和 JavaScript 文件。所以，虽然 WebGL 网页更加复杂了，但它仍然保持着与传统的动态网页相同的结构:只用到 HTML 文件和 JavaScript文件。

WebGL入门

WebGL采用HTML5 中新引人的<canvas>元素(标签)定义了网页上的绘图区域。如果没有 WebGL，JavaScript 只能在<canvas>上绘制二维图形，有了 WebGL，就可以在上面绘制三维图形了。

最短的WebGL程序：清空绘图区

<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <title>使用指定颜色清空画布</title>
</head>
<body onload="main()">
<canvas id="example" width="400" height="400">
    请使用支持canvas的浏览器
</canvas>
</body>
<script src="../lib/webgl-utils.js"></script>
<script src="../lib/webgl-debug.js"></script>
<script src="../lib/cuon-utils.js"></script>
<script src="clearCanvas.js"></script>
</html>

function main(){
    const canvas = document.getElementById("example");
    // 获取二维图形的绘图上下文
    const gl = getWebGLContext(canvas);
    if(!gl){
        console.error("webgl渲染失败");
        return;
    }

    // 指定清空画布所用的颜色
    gl.clearColor(0, 0, 1, 1);
    // 使用上面指定的颜色清空画布
    gl.clear(gl.COLOR_BUFFER_BIT);
}

绘制图形(2d和3d)三步骤:

获取 canvas 元素

获取绘图上下文

开始绘图

关于绘图上下文

在获取 WebGL 绘图上下文时，canvas.getContex() 函数接收的参数，在不同浏览器中会不同，所以书中写了一个函数 getwebGLContext 来隐藏不同浏览器之间的差异。

// 核心代码
var create3DContext = function(canvas, opt_attribs) {
  var names = ["webgl", "experimental-webgl", "webkit-3d", "moz-webgl"];
  var context = null;
  for (var ii = 0; ii < names.length; ++ii) {
    try {
      context = canvas.getContext(names[ii], opt_attribs);
    } catch(e) {}
    if (context) {
      break;
    }
  }
  return context;
}

设置<canvas>的背景色

在清空绘图区之前，你可以指定背景色

一旦指定了背景色之后，背景色就会驻存在 WebGL 系统(WebGL System)中，在下次调用 gl.clearcolor() 方法前不会改变。换句话说，如果将来什么时候你还想用同一个颜色再清空一次绘图区，没必要再指定一次背景色。

清空<canvas>

调用 gl.clear() 函数，用之前指定的背景色清空 (即用背景色填充,擦除已经绘制的内容)绘图区域。

函数的参数是 gl.COLOR_BUEEER_BIT，而不是 (你可能认为会是)表示绘图区域的canvas，这是因为 WebGL 中的 gl.clear() 方法实际上继承自 OpenGL，它基于多基本缓冲区模型，这可比二维绘图上下文复杂得多。清空绘图区域，实际上是在清空须色缓冲区(color buffer)，传递参数 gl.COLOR_BUEEER_BIT 就是在告诉 WebGL 清空颜色缓冲区。除了颜色缓冲区，WebGL 还会使用其他种类的缓冲区，比如深度缓冲区和模板缓冲区。深度缓冲区将在“进入三维世界”中解释。由于模板缓冲区很少被使用，因为它本书将不会涉及。

清空颜色缓冲区将导致 WebGL 清空页面上的canvas区城。

如果没有指定背景色 (也就是说，你没有调用 gl.clearcolor())，那么使用的默认值如下所示。

绘制一个点（版本1）

<!DOCTYPE html>
<html lang="en">
  <head>
    <meta charset="utf-8" />
    <title>Draw a point (1)</title>
  </head>

  <body onload="main()">
    <canvas id="webgl" width="400" height="400">
    Please use a browser that supports "canvas"
    </canvas>

    <script src="../lib/webgl-utils.js"></script>
    <script src="../lib/webgl-debug.js"></script>
    <script src="../lib/cuon-utils.js"></script>
    <script src="HelloPoint1.js"></script>
  </body>
</html>

// HelloPoint1.js (c) 2012 matsuda
// 顶点着色程序
var VSHADER_SOURCE = 
  'void main() {\n' +
  '  gl_Position = vec4(0.0, 0.0, 0.0, 1.0);\n' + // 设置坐标，必须有值
  '  gl_PointSize = 10.0;\n' +                    // 设置尺寸，默认为1.0
  '}\n';

// 片源着色器程序
var FSHADER_SOURCE =
  'void main() {\n' +
  '  gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' + // 设置颜色
  '}\n';

function main() {
  // 获取 canvas 元素
  var canvas = document.getElementById('webgl');

  // 获取WebGL绘图上下文
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // 初始化着色器
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // 设置 canvas的背景色
  gl.clearColor(0.0, 0.0, 0.0, 1.0);

  // 清空 canvas
  gl.clear(gl.COLOR_BUFFER_BIT);

  // 绘制一个点
  gl.drawArrays(gl.POINTS, 0, 1);
}

// cuon-utils.js (c) 2012 kanda and matsuda
/**
 * Create a program object and make current
 * @param gl GL context
 * @param vshader a vertex shader program (string)
 * @param fshader a fragment shader program (string)
 * @return true, if the program object was created and successfully made current 
 */
function initShaders(gl, vshader, fshader) {
  var program = createProgram(gl, vshader, fshader);
  if (!program) {
    console.log('Failed to create program');
    return false;
  }

  gl.useProgram(program);
  gl.program = program;

  return true;
}

/**
 * Create the linked program object
 * @param gl GL context
 * @param vshader a vertex shader program (string)
 * @param fshader a fragment shader program (string)
 * @return created program object, or null if the creation has failed
 */
function createProgram(gl, vshader, fshader) {
  // Create shader object
  var vertexShader = loadShader(gl, gl.VERTEX_SHADER, vshader);
  var fragmentShader = loadShader(gl, gl.FRAGMENT_SHADER, fshader);
  if (!vertexShader || !fragmentShader) {
    return null;
  }

  // Create a program object
  var program = gl.createProgram();
  if (!program) {
    return null;
  }

  // Attach the shader objects
  gl.attachShader(program, vertexShader);
  gl.attachShader(program, fragmentShader);

  // Link the program object
  gl.linkProgram(program);

  // Check the result of linking
  var linked = gl.getProgramParameter(program, gl.LINK_STATUS);
  if (!linked) {
    var error = gl.getProgramInfoLog(program);
    console.log('Failed to link program: ' + error);
    gl.deleteProgram(program);
    gl.deleteShader(fragmentShader);
    gl.deleteShader(vertexShader);
    return null;
  }
  return program;
}


/**
 * Create a shader object
 * @param gl GL context
 * @param type the type of the shader object to be created
 * @param source shader program (string)
 * @return created shader object, or null if the creation has failed.
 */
function loadShader(gl, type, source) {
  // Create shader object
  var shader = gl.createShader(type);
  if (shader == null) {
    console.log('unable to create shader');
    return null;
  }

  // Set the shader program
  gl.shaderSource(shader, source);

  // Compile the shader
  gl.compileShader(shader);

  // Check the result of compilation
  var compiled = gl.getShaderParameter(shader, gl.COMPILE_STATUS);
  if (!compiled) {
    var error = gl.getShaderInfoLog(shader);
    console.log('Failed to compile shader: ' + error);
    gl.deleteShader(shader);
    return null;
  }

  return shader;
}

着色器

要使用WebGL进行绘图就必须使用着色器。在代码中,着色器程序是以字符串的形式“嵌人”在 JavaScript 文件中的，在程序真正开始运行前它就已经设置好了。

WebGL需要两种着色器

顶点着色器(Vertexshader)：顶点着色器是用来描述顶点特性（如位置、颜色等）的程序。顶点(vertex)是指二维或三维空间中的一个点，比如二维或三维图形的端点或交点。

片元着色器(Fragment shader)：进行逐片元处理过程如光照（见“光照”）的程序。片元(fragment)是一个WebGL术语,你可以将其理解为像素(图像的单元)。

简单地说，在三维场景中，仅仅用线条和颜色把图形画出来是远远不够的。你必须考虑，比如，光线照上去之后，或者观察
者的视角发生变化，对场景会有些什么影响。着色器可以高度灵活地完成这些工作，提供各种渲染效果。这也就是当今计算机制作出的三维场景如此逼真和令人震撼的原因。

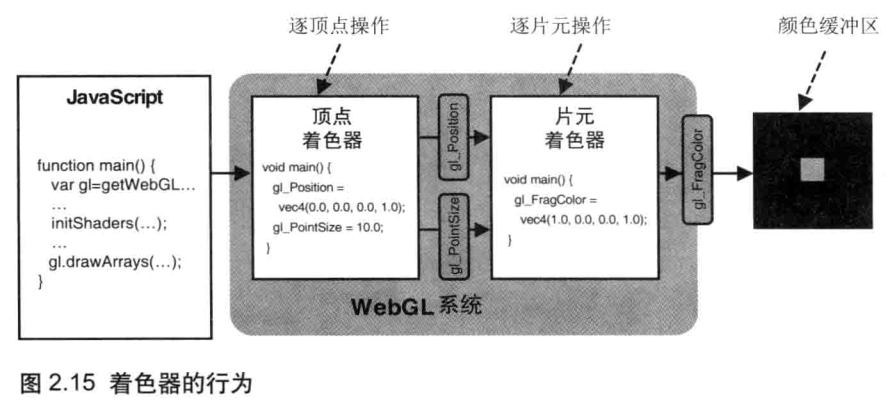
下图显示了程序的执行流程：从执行JavaScript，到在WebGL系统中使用着色器在浏览器上绘制图形。

程序执行的流程大概是：首先运行 JavaScript 程序，调用WebGL的相关方法，然后顶点着色器和片元着色器就会执行，在颜色缓冲区内进行绘制，这时就清空了绘图区；最后，颜色缓冲区中的内容会自动在浏览器的 canvas 上显示出来。

示例程序的任务是，在屏幕上绘制一个10像素大小的点，它用到两个着色器:

顶点着色器指定了点的位置和尺寸。本例中，点的位置是(0.0，0.0，0.0)，尺寸是10.0像素。

片元着色器指定了点的颜色。本例中，点的颜色是红色(1.0，0.0，0.0，1.0)。

使用着色器的WebGL 程序的结构

着色器是以 JavaScript 字符串形式编写的着色器语言程序，这样主程序就可以将他们传给WebGL 系统。

因为着色器程序代码必须预先处理成单个字符串的形式，所以我们用+号将多行字符串连成一个长字符串。每一行以\n 结束，这是由于当着色器内部出错时，就能获取出错的行号，这对于检查源代码中的错误很有帮助。但是，\n 并不是必须的，你自己编写
着色器时，也可以不用它。

初始化着色器

书中初始化着色器辅助函数 initShaders 说明如下：

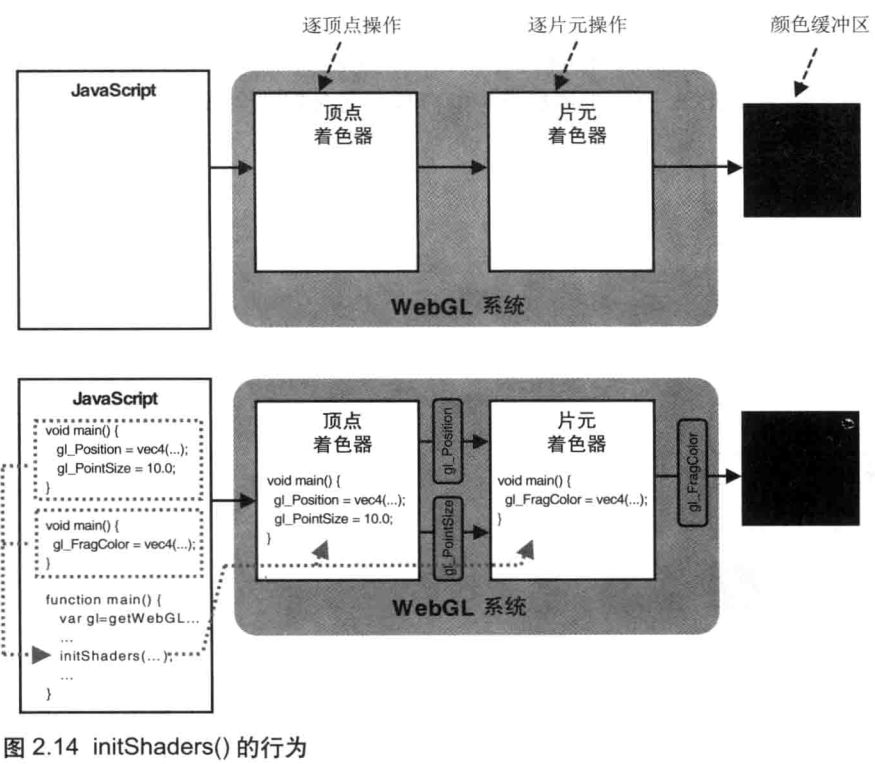
如图2.14中的上方图所示，WebGL系统由两部分组成，即顶点着色器和片元着色器。在初始化着色器之前，顶点着色器和片元着色器都是空白的，我们需要将字符串形式的着色器代码从JavaScript传给WebGL系统，并建立着色器，这就是initShaders()所做的事情。注意,着色器运行在 WebGL 系统中，而不是JavaScript程序中。

图2.14下方图显示了initShaders()执行后的情形，着色器程序以字符串的形式传给initShaders(),然后在WebGL系统中，着色器就建立好了并随时可以使用。如图所示，顶点着色器先执行，它对glPosition变量和glPointSize变量进行赋值，并将它们传入片元着色器，然后片元着色器再执行。

WebGL程序包括运行在浏览器中的JavaScript和运行在WebGL系统的着色器程序这两个部分。

绘制一个点，在初始化中需要设置三项信息：位置，尺寸和颜色，指定三项信息的方式如下：

顶点着色器将指定点的位置和尺寸，在这个示例程序中，点的位置是(000.00.0)
而点的尺寸是10.0。

片元着色器将指定点的颜色。在示例程序中，点的颜色是红色(10,00,001.0)。

顶点着色器

顶点着色器设置了点的位置和颜色

顶点着色器程序，和C语言程序一样，必须包含一个main()函数。main()前面的关键字void表示这个函数不会有返回值。还有，你不能为main()指定参数。

就像JavaScript一样，着色器程序使用=操作符为变量赋值。首先将点的位置赋值给gl_Position变量，然后将点的尺寸赋值给gl_PointSize，这两个变量是内置在顶点着色器中的，而且有着特殊的含义：gl_Position表示顶点的位置(这里，就是要绘制的点的位置)，gl_Pointsize表示点的尺寸，如下图所示。

注意，gl_Position变量必须被赋值，否则着色器就无法正常工作。相反，gl_Pointsize并不是必须的，如果你不赋值，着色器就会为其取默认值1.0。

和JavaScript不同，GLSLES是一种强类型的编程语言，也就是说，开发者需要明确指出某个变量是某种“类型”的，C和Java就是这样的语言。通过为变量指定类型，系统就能够轻易理解变量中存储的是何种数据，进而优化处理这些数据。表2.3总结了这一节出现在GLSLES代码中的几种类型。

注意，如果向某类型的变量赋一个不同类型的值，就会出错。例如，glPointSize是浮点型的变量，你就必须向其赋浮点型的值。

另一个内置变量gl_Position表示点的位置，其类型为vec4；vec4是由4个浮点数组成的矢量。但是，我们这里只有三个浮点数(0.0,0.0,0.0)，即X，Y和Z坐标值，需要用某种方法将其转化为vec4类型的变量。好在着色器提供了内置函数vec4()帮助你创建vec4类型的变量

注意，赋给gl_Position的矢量中，我们添加了1.0作为第4个分量。由4个分量组成的矢量被称为齐次坐标(参阅下方表格中的文字)，因为它能够提高处理三维数据的效率，所以在三维图形系统中被大量使用。虽然齐次坐标是四维的，但是如果真最后一个分量是 1.0，那么这个齐次坐标就可以表示“前三个分量为坐标值”的那个点。所以，当你需要用齐次坐标表示顶点坐标的时候，只要将最后一个分量赋为 1.0 就可以了。

片元着色器

顶点着色器控制点的位置和大小，片元着色器控制点的颜色。如前所述，片元就是显示在屏幕上的一个像素(严格意义上来说，片元包括这个像素的位置、颜色和其他信息)。

片元着色器将点的颜色赋值给 gl_FragColor 变量，该变量是片元着色器唯一的内置变量，它控制着像素在屏幕上的最终颜色，如表2.4所示。

对这个内置变量赋值后，相应的像素就会以这个颜色值显示。和顶点着色器中的顶点位置一样，颜色值也是vec4类型的，包括四个浮点型分量，分别代表RGBA值。本例我们赋的颜色值为(1.0,0.0,0.0,1.0)，所以点是红色的。

绘制操作

建立了着色器之后，我们就需要进行绘制操作，在这个例子中，就是画一个点。首先需要清空绘制区域。然后，我们使用gl.drawArrays()来进行绘制；

gl.drawArrays()是一个强大的函数，它可以用来绘制各种图形，该函数的规范如下表所示。

当程序调用gl.drawArrays()时，顶点着色器将被执行 count 次，每次处理一个顶点。在这个示例程序中，着色器只执行一次(count被设置为1)，我们只绘制一个点。在着色器执行的时候，将调用并逐行执行内部的 main () 函数，将值 (0.0, 0.0, 0.0, 1.0) 赋给gl_Position ，将值 10.0 赋给 gl_Pointsize 。

一旦顶点着色器执行完后，片元着色器就会开始执行，调用main()函数,将颜色值(红色)赋给gl_FragColor。最后，一个红色的10个像素大的点就被绘制在了(0.00.0001.0)处，也就是绘制区域的中心位置。

WebGL坐标系统

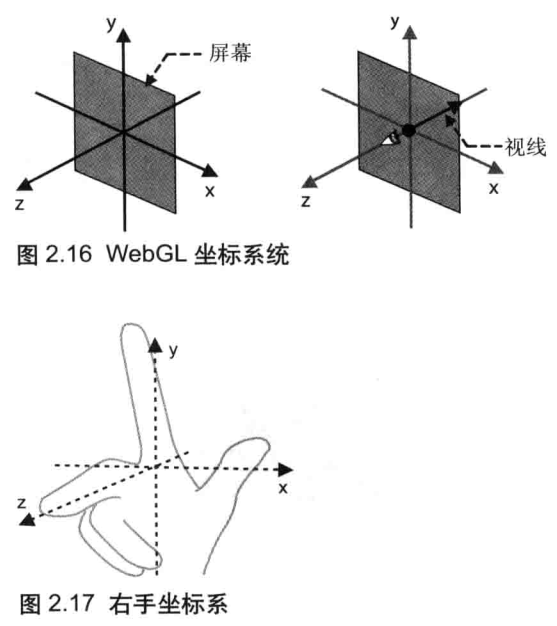
由于WebGL处理的是三维图形，所以它使用三维坐标系统(笛卡尔坐标系)，具有X轴、Y轴和Z轴。一维坐标系统很容易理解，因为我们的世界也是三维的:具有宽度高度和长度。在任何坐标系统中，轴的方向都非常重要。通常，在 WebGL 中，当你面向计算机屏幕时，X轴是水平的(正方向为右)，Y轴是垂直的(正方向为下)，而Z轴垂直于屏幕(正方向为外)，如图2.16左所示。观察者的眼睛位于原点(0.0.0.0.0.0)处，视线则是沿着Z轴的负方向，从你指向屏幕(图2.16右)。这套坐标系又被称为右手坐标系(right-handed coordinate system)，因为可以用右手来表示，如图2.17所示。默认情况下WebGL 使用右手坐标系，右手坐标系也会贯穿本书始终。然而，事实远远比这复杂。实际上，WebGL 本身既不是右手坐标系，又不是左手坐标系的。附录D“WebGL/OpenGL:左手坐标系还是右手坐标系?”详细地阐述了这一点。现在，你认为WebGL是右手坐标系的也完全没有关系。

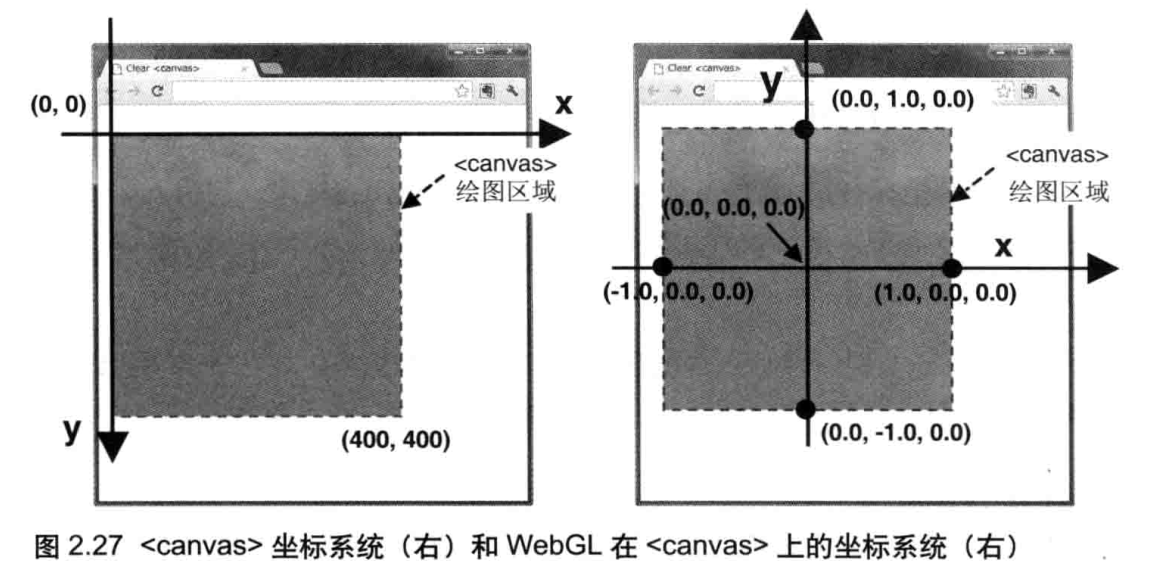
cavas坐标系：横轴为x轴 (正方向朝右)，纵轴为y轴 (正方向朝下)。原点落在左上方。
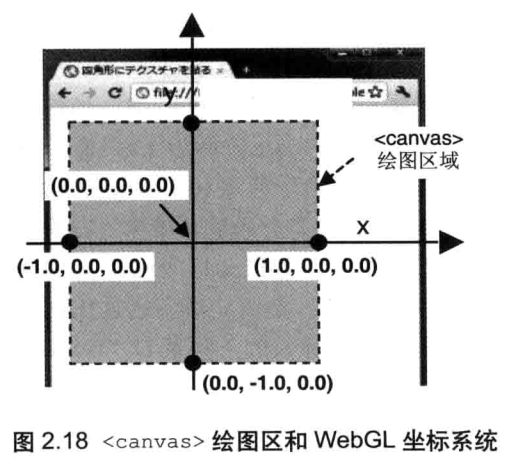
如图所示，WebGL 的坐标系和 canvas 绘图区的坐标系不同，需要将前者映射到后者。默认情况下，如图2.18所示，WebGL坐标与 canvas坐标的对应关系如下。

canvas 的中心点:对应WebGL坐标(0.0,0.0,0.0)

canvas 的上边缘和下边缘:对应WebGL坐标(-1.0，0.0，0.0)和(1.0，0.0，0.0)

canvas 的左边缘和右边缘:对应WebGL坐标(0.0，-1.0，0.0)和(0.0，1.0，0.0)

绘制一个点（版本2）

这一节将讨论如何在 JavaScript 和着色器之间传输数据，因为点的位置是直接编写 (“硬编码”)在顶点着色器中的;

在这一节中你将看到，WebGL程序可以将顶点的位置坐标从 JavaScript 传到着色器程序中，然后在对应位置上将点绘制出来。

// HelloPint2.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE = 
  'attribute vec4 a_Position;\n' + // attribute variable
  'void main() {\n' +
  '  gl_Position = a_Position;\n' +
  '  gl_PointSize = 10.0;\n' +
  '}\n'; 

// Fragment shader program
var FSHADER_SOURCE = 
  'void main() {\n' +
  '  gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // 在着色器程序（program）中获取指定名称的顶点着色器变量地址，估计是数组地址
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if (a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return;
  }

  // 把顶点位置传给attribute变量。1f表示1个浮点数，如此类推
  gl.vertexAttrib3f(a_Position, 0.0, 0.0, 0.0);

  // Specify the color for clearing <canvas>
  gl.clearColor(0.0, 0.0, 0.0, 1.0);

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);
    
  // Draw
  gl.drawArrays(gl.POINTS, 0, 1);
}

使用attribute 变量

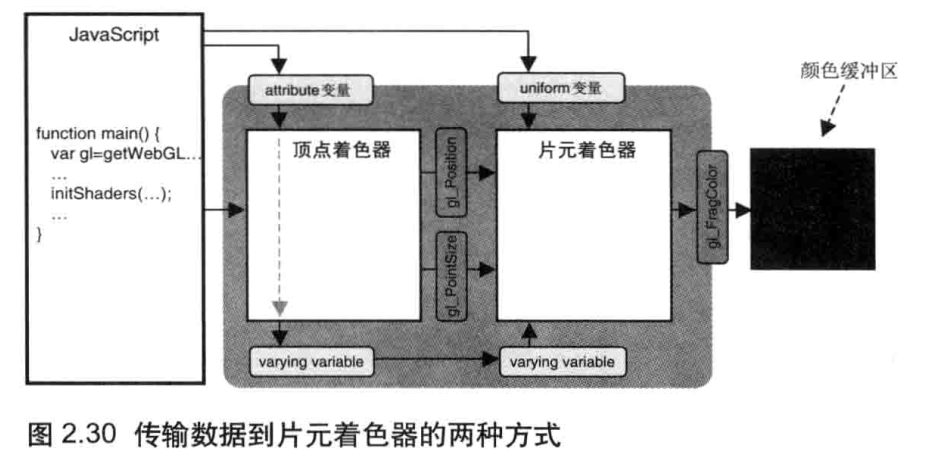
我们的目标是，将位置信息从 JavaScript 程序中传给顶点着色器。有两种方式可以做到这点：attribute 变量和 uniform 变量，如图 2.20 所示。使用哪一个变量取决于需传输的数据本身，attribute 变量传输的是那些与顶点相关的数据，而 uniform 变量传输的是那些对于所有顶点都相同 (或与顶点无关)的数据。本例将使用 attribute 变量来传输顶点坐标，显然不同的顶点通常具有不同的坐标.

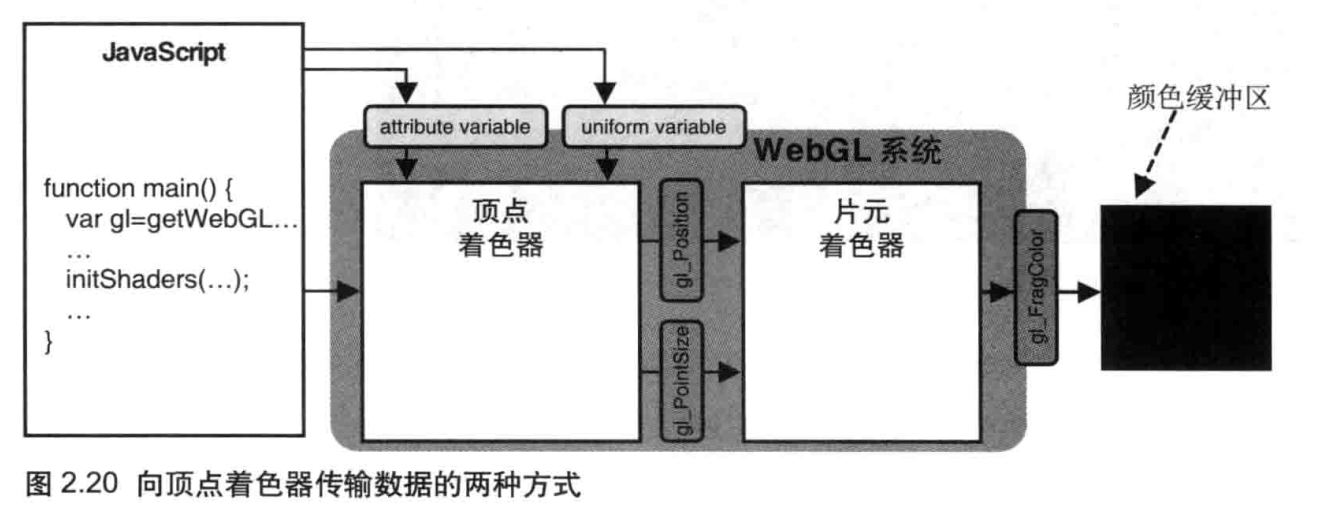
attribute 变量是一种 GLSL ES 变量，顶点着色器能使用它被用来从外部向顶点着色器内传输数据，只有顶点着色器能使用它。

为了使用 attribute 变量，示例程序需要包含以下步骤

在顶点着色器中，声明 attribute 变量;

将 attribute 变量赋值给 gl_Position 变量;

向 attribute 变量传输数据

'attribute vec4 a_Position;\n'

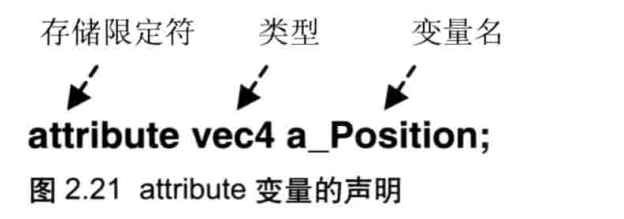
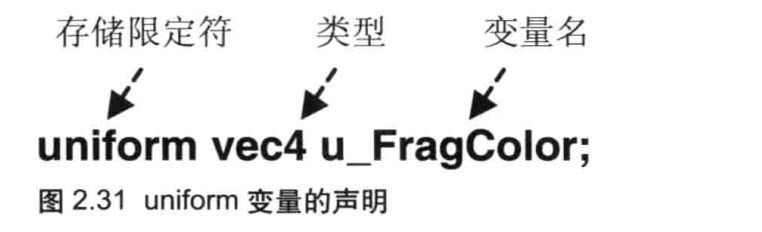
在这一行中，关键词 attribute 被称为存储限定符(storage qualifer)，它表示接下来的变量(在这个例子中是 a Position)个 attribute 变量。attribute 变量必须声明成全局变量，数据将从着色器外部传给该变量。变量的声明必须按照以下的格式:

< 存储限定符><类型><变量名 >，如图 2.21 所示

attribue 变量a_position (第4行)的类型是 vec4，如表 2.2 所示。它将被赋值给gl Position，后者的类型也是 vec4。

一旦声明 a_Position 之后，我们将其赋值给 gl_Position :

'  gl_Position = a_Position;\n'

这样就完成了着色器部分，它已经准备好从外部接收顶点坐标了。接下来，我们需要将数据从 JavaScript 中传给着色器的 attribute 变量。

获取attribute 变量的存储位置

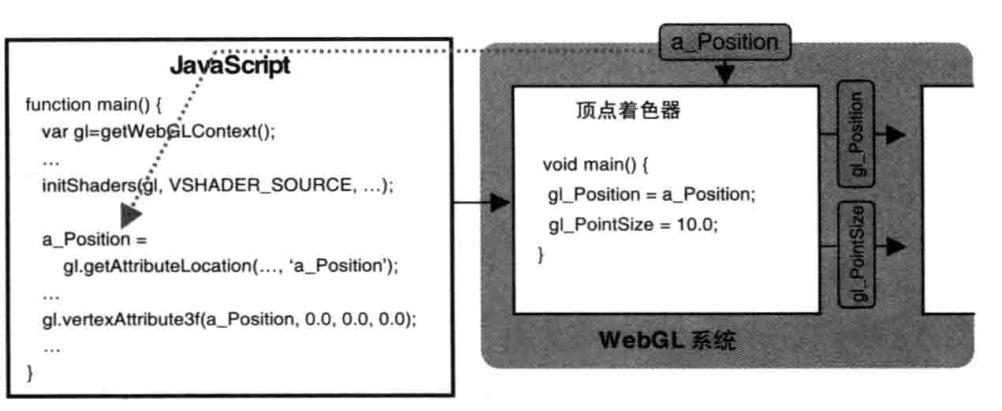
如前所述，我们使用辅助函数 initShaders() 在 WebGL 系统中建立了顶点着色器然后，WebGL 就会对着色器进行解析，辨识出着色器具有的 attribute 变量，每个变量都具有一个存储地址，以便通过存储地址向变量传输数据。比如，当你想要向顶点着色器的 a_Position 变量传输数据时，首先需要向 WebGL 系统请求该变量的存储地址。我们使用 gl.getAttribLocation() 来获取 attribute 变量的地址。

 var a_Position = gl.getAttribLocation(gl.program, 'a_Position');

方法的第一个参数是一个程序对象(program object)，它包括了顶点着色器和片元着色器，注意你必须在调用 initShader() 之后再访问 gl.program，因为是 initShader()函数创建了这个程序对象。第二个参数是想要获取存储地址的 attribute 变量的名称。

方法的返回值是 attribute 变量的存储地址。

向attribute 变量赋值

一旦将 attribute 变量的存储地址保存在JavaScript 变量a_Position 中，下面就需要使用该变量来向着色器传人值。我们使用 gl.vertexAttrib3f() 函数来完成这一步。

gl.vertexAttrib3f(a_Position, 0.0, 0.0, 0.0);

该函数的第1个参数是 attribute 变量的存储地址，即 gl.getAttribLocation() 的返回值 ;第2、3、4个参数是三个浮点型数值，即点的x、y和z坐标值。函数被调用后，这三个值被一起传给顶点着色器中的 a_Position 变量。图2.22 显示了获取 attribute 变量的存储地址并向其传值的过程.

你可能已经注意到， a_Position 变量是 vec4 类型的，但是 gl.vertexAttrib3f() 仅传了三个分量值(x、y和z)而不是4个；实际上，如果你省略了第 4 个参数，这个方法就会默认地将第 4个分量设置为了 1.0，如图 2.23 所示。颜色值的第 4 个分量为 1.0 表示该颜色完全不透明，而齐次坐标的第 4个分量为 1.0 使齐次坐标与三维坐标对应起来，所以 1.0 是一个“安全”的第 4分量。

gl.vertexAttrib3f() 的同族函数

gl.vertexAttrib3f() 是一系列同族函数中的一个， 该系列函数的任务就是从 javascript 向顶点着色器中的 attribute 变量传值。 gl.vertexAttriblf() 传输 1个单精度值 (v0)，gl.vertexAttrib2f() 传输2 个值 (v0和vl)，而gl.vertexAttrib4f() 传输 4个值 (v0、v1、v2和v3)。

你也可以使用这些方法的矢量版本，它们的名字以“v”(vector) 结尾，并接受类型化数组 (见第 4 章)作为参数，函数名中的数字表示数组中的元素个数（实际上这里数字 4 的真正含义是 attribute 矢量中的元素个数（即多少个元素表示为一个矢量），并不是数组的元素个数，但这里我们只绘制一个顶点，所以二者相等。）。比如：

var position = new Float32Array([1.0,2.0,3.0,1.0]);
gl.vertexAttrib4fv(a_Position,position)

通过鼠标点击绘点

这一节，拓展 JavaScript 传输数据到顶点着色器的能力:在鼠标点击的位置上绘制出点来。

// ClickedPints.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'void main() {\n' +
  '  gl_Position = a_Position;\n' +
  '  gl_PointSize = 10.0;\n' +
  '}\n'

// Fragment shader program
var FSHADER_SOURCE =
  'void main() {\n' + '  gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' + '}\n'

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl')

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas)
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL')
    return
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.')
    return
  }

  // // Get the storage location of a_Position
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position')
  if (a_Position < 0) {
    console.log('Failed to get the storage location of a_Position')
    return
  }

  // Register function (event handler) to be called on a mouse press
  canvas.onmousedown = function (ev) {
    click(ev, gl, canvas, a_Position)
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0.0, 0.0, 0.0, 1.0)

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT)
}

var g_points = [] // The array for the position of a mouse press
function click(ev, gl, canvas, a_Position) {
  var x = ev.clientX // 鼠标相对于屏幕的水平坐标
  var y = ev.clientY // 鼠标相对于屏幕的垂直坐标
  var rect = ev.target.getBoundingClientRect() // canvas对象的位置信息

   // (x - rect.left)：鼠标在x轴方向上的偏移，相当于canvas的x轴坐标
  x = (x - rect.left - canvas.width / 2) / (canvas.width / 2)
  // (y - rect.top)：鼠标在y轴方向上的偏移，相当于canvas的y轴坐标
  y = (canvas.height / 2 - (y - rect.top)) / (canvas.height / 2)
  // 将坐标存储在 g_points 数组中
  g_points.push(x)
  g_points.push(y)

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);

  var len = g_points.length
  for (var i = 0; i < len; i += 2) {
    // Pass the position of a point to a_Position variable
    gl.vertexAttrib3f(a_Position, g_points[i], g_points[i + 1], 0.0)

    // Draw
    gl.drawArrays(gl.POINTS, 0, 1)
  }
}

响应鼠标点击事件

关于点击坐标

鼠标点击位置的信息存储在事件对象 ev 中，该对象传给了 click()函数，可以通过访问 ev.clientx和 ev.clientY 来获取位置坐标。但是，由于以下两点原因，我们不能直接使用这两个坐标值 :

鼠标点击位置坐标是在“浏览器客户区”(client area) 中的坐标，而不是在<canvas>中的(如图 2.26 所示)

<canvas> 的坐标系统与 WebGL 的坐标系统 (如图 2.27 所示)，其原点位置和 Y轴的正方向都不一样。

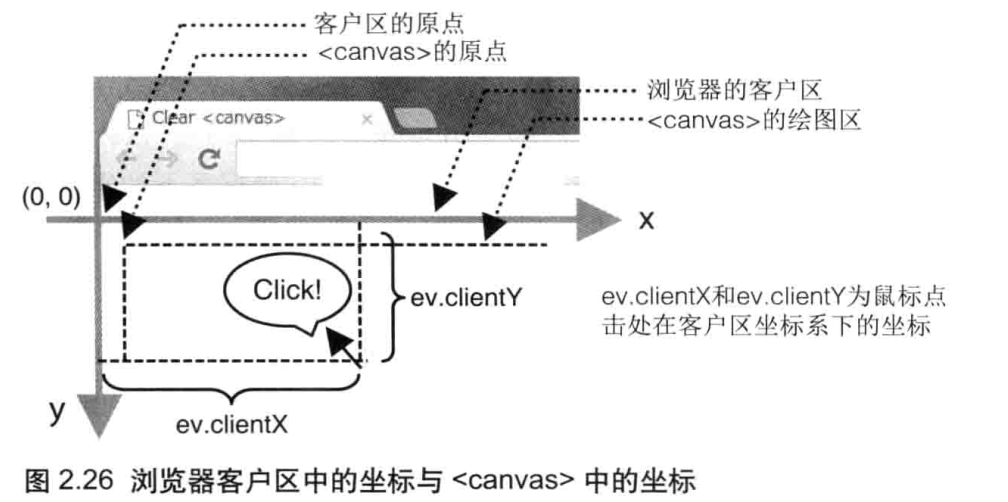
你需要将坐标从浏览器客户区坐标系下转换到<canvas>坐标系下，然后再转换到 WebGL 坐标系下。

首先，获取 <canvas>在浏览器客户区中的坐标，rect.left 和 rect.top是 <canvas>的原点在浏览器客户区中的坐标，如图2.26 所示，这样(x-rect.left)和(y-rect.top) 就可以将客户区坐标系下的坐标(xy)转换为<canvas>坐标系下的坐标了。

接下来，将<canvas>坐标系下的坐标转换到 WebGL 坐标系统中，如图 2.27 所示。为了进行这一步转换，你需要知道<canvas>的中心点。我们通过 canvas.height (这里是 400)和 canvas.width (也是 400)获取 <canvas>的宽度和高度，而中心点的坐标是(canvas .height/2， canvas .width/2)。然后，你就可以使用 ((x-rect.left)-canvas.width/2)和(canvas.height/2-(y-rect.top))将<canvas>的原点平移到中心点 (WebGL 坐标系统的原点位于此处)。

接着，如图 2.27 所示，<canvas>的x轴坐标区间为从0到 canvas.width (400)，而其y轴区间为从0到 canvas.height(400)。因为 WebGL 中轴的坐标区间为从-1.0到1.0.所以最后一步我们将x坐标除以 canvas.width/2，将y坐标除以 canvas.height/2，将<canvas>坐标映射到 WebGL 坐标。

关于存储每次点击坐标

这里会把鼠标每次点击的位置都记录下来，而不是仅仅记录最近次鼠标点击的位置。

这是因为 WebGL 使用的是颜色缓冲区。系统中的绘制操作实际上是在颜色缓冲区中进行绘制的，绘制结束后系统将缓冲区中的内容显示在屏幕上，然后颜色缓冲区就会被重置，其中的内容会丢失 (这是默认操作下.一章将详细讨论)。因此，我们有必要将每次鼠标点击的位置都记录下来，鼠标每次点击之后，程序都重新绘制了(从第 1次点击到最近一次的)所有的点。比如，第1次点击鼠标，绘制第1个点;第2 次点击鼠标，绘制第1个和第 2个点;第3次点击鼠标绘制第 1、2 个和第 3 个点，以此类推。

改变点的颜色

构建一个更复杂的程序一一改变绘制点的颜色，而且点的颜色依赖于它在 <canvas>中的位置

// ColoredPoint.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'void main() {\n' +
  '  gl_Position = a_Position;\n' +
  '  gl_PointSize = 10.0;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  'precision mediump float;\n' +
  'uniform vec4 u_FragColor;\n' +  // uniform変数
  'void main() {\n' +
  '  gl_FragColor = u_FragColor;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // // Get the storage location of a_Position
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if (a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return;
  }

  // Get the storage location of u_FragColor
  var u_FragColor = gl.getUniformLocation(gl.program, 'u_FragColor');
  if (!u_FragColor) {
    console.log('Failed to get the storage location of u_FragColor');
    return;
  }

  // Register function (event handler) to be called on a mouse press
  canvas.onmousedown = function(ev){ click(ev, gl, canvas, a_Position, u_FragColor) };

  // Specify the color for clearing <canvas>
  gl.clearColor(0.0, 0.0, 0.0, 1.0);

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);
}

var g_points = [];  // The array for the position of a mouse press
var g_colors = [];  // The array to store the color of a point
function click(ev, gl, canvas, a_Position, u_FragColor) {
  var x = ev.clientX; // x coordinate of a mouse pointer
  var y = ev.clientY; // y coordinate of a mouse pointer
  var rect = ev.target.getBoundingClientRect();

  x = ((x - rect.left) - canvas.width/2)/(canvas.width/2);
  y = (canvas.height/2 - (y - rect.top))/(canvas.height/2);

  // Store the coordinates to g_points array
  g_points.push([x, y]);
  // Store the coordinates to g_points array
  if (x >= 0.0 && y >= 0.0) {      // First quadrant
    g_colors.push([1.0, 0.0, 0.0, 1.0]);  // Red
  } else if (x < 0.0 && y < 0.0) { // Third quadrant
    g_colors.push([0.0, 1.0, 0.0, 1.0]);  // Green
  } else {                         // Others
    g_colors.push([1.0, 1.0, 1.0, 1.0]);  // White
  }

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);

  var len = g_points.length;
  for(var i = 0; i < len; i++) {
    var xy = g_points[i];
    var rgba = g_colors[i];

    // Pass the position of a point to a_Position variable
    gl.vertexAttrib3f(a_Position, xy[0], xy[1], 0.0);
    // Pass the color of a point to u_FragColor variable
    gl.uniform4f(u_FragColor, rgba[0], rgba[1], rgba[2], rgba[3]);
    // Draw
    gl.drawArrays(gl.POINTS, 0, 1);
  }
}

可以用 uniform 变量将颜色值传给着色器，其步骤与用 atrribute 变量传递的类似。不同的仅仅是，这次数据传输的目标是片元着色器，而非顶点着色器

在片元着色器中准备 uniform 变量。

用这个 uniform 变量向 gl FragColor 赋值。

将颜色数据从 JavaScript 传给该 uniform 变量。

uniform 变量

我们已经知道了如何从 JavaScript中向顶点着色器的 attribute变量传数据。不幸的是只有顶点着色器才能使用 attribute 变量，使用片元着色器时，你就需要使用 uniform 变量。或者，你可以使用 varying 变量，如图 2.30 底部所示。但是这比较复杂，我们在第 5章之前不会使用它。

之前介绍 attribute 变量的概念时曾经提到过，uniform变量用来从 JavaScript程序向顶点着色器和片元着色器传输“一致的”(不变的)数据。

在使用 uniform 变量之前，首先需要按照与声明 attribute 变量相同的格式<存储限定符 >< 类型 >< 变量名 >(如图 2.3所示) 来声明 uniform 变量。

 'precision mediump float;\n' +
 'uniform vec4 u_FragColor;\n' +  // uniform変数

注意：使用精度限定词(precision qualifier) 来指定变量的范围 (最大值与最小值)和精度，本例中为中等精度。第 5 章将会详细讨论精度的问题。

获取uniform 变量的存储地址

可以使用以下方法来获取uniform变量的存储地址

这个函数的功能和参数与 gl.getAttribLocation() 一样，但是如果 uniform变量不存在或者其命名使用了保留字前缀，那么函数的返回值将是 null 而不是 -1(gl.getAttribLocation() 在此情况下返回 -1)。因此，在获取 umiform 变量的存储地址后，你需要检查其是否为 null。

向uniform 变量赋值

有了 uniform变量的存储地址，就可以使用 WebGL 函数 gl.uniform4f()向变量中写入数据。该函数的功能和参数与 gl.vertexAttrib[1234]f() 很相似。

gl.uniform4f() 的同族函数

gl.uniform4f() 也有一系列同族函数。gl.uniform1f() 函数用来传输1个值(v0),gl.uniform2f() 传输2个值(v0和vl)，gl.uniform3f()传输3个值 (v，vl和v2)。

绘制和变换三角形

绘制多个点

构成三维模型的基本单位是三角形，不管三维模型的形状多么复杂，其基本组成部分都是三角形，只不过复杂的模型由更多的三角形构成而已。通过创建更细小和更大量的三角形，就可以创建更复杂利口更逼真的三维模型。

前一章有一个示例程序ClickedPoints，它在鼠标点击的位置绘制点。Clicked-Points将所有点的坐标数据存储在一个JavaScript数组g_points[]中，然后使用了一个循环遍历该数组，每次遍历就向着色器传入一个点，并调用gldrawArrays()将这个点绘制出来。

显然，这种方法只能绘制一个点。对那些由多个顶点组成的图形，比如三角形、矩形和立方体来说，你需要一次性地将图形的顶点全音部传入顶点着色器，然后才能把图形画出来。

WebGL提供了一种很方便的机制，即缓冲区对象(buffer object)，它可以一次性地向着色器传入多个顶点的数据。缓冲区对象是WebGL 系统中的一块内存区域，我们可以一次性地向缓冲区对象中填充大量的顶点数据，然后将这些数据保存在其中，供顶点着色器使用。

// MultiPoint.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'void main() {\n' +
  '  gl_Position = a_Position;\n' +
  '  gl_PointSize = 10.0;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  'void main() {\n' +
  '  gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // 设置顶点位置
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the positions of the vertices');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0, 0, 0, 1);

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);

  // 绘制3个点
  gl.drawArrays(gl.POINTS, 0, n);
}

function initVertexBuffers(gl) {
  var vertices = new Float32Array([
    0.0, 0.5,   -0.5, -0.5,   0.5, -0.5
  ]);
  var n = 3; // 点个数

  // 创建缓冲区对象
  var vertexBuffer = gl.createBuffer();
  if (!vertexBuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // 将缓冲区对象绑定到目标
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
  // 向缓冲区对象写入数据
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);

  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if (a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  // 将缓冲区对象分配给a_Position变量
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);

  // 连接a_Position变量与分配给它的缓冲区对象
  gl.enableVertexAttribArray(a_Position);

  return n;
}

使用缓冲区对象

使用缓冲区对象向顶点着色器传入多个顶点的数据，需要遵循以下五个步骤。处理其他对象,如纹理对象(第4章)，帧缓冲区对象(第8章“光照”)时的步骤也比较类似：

创建缓冲区对象(g1.createBuffer())。

绑定缓冲区对象(g1.bindBuffer())。

将数据写人缓冲区对象(g1.bufferData())。

将缓冲区对象分配给一个 attribute 变量( gl.vertexAttribPointer() )。

开启 attribute 变量( gl.enableVertexAttribArray() )。

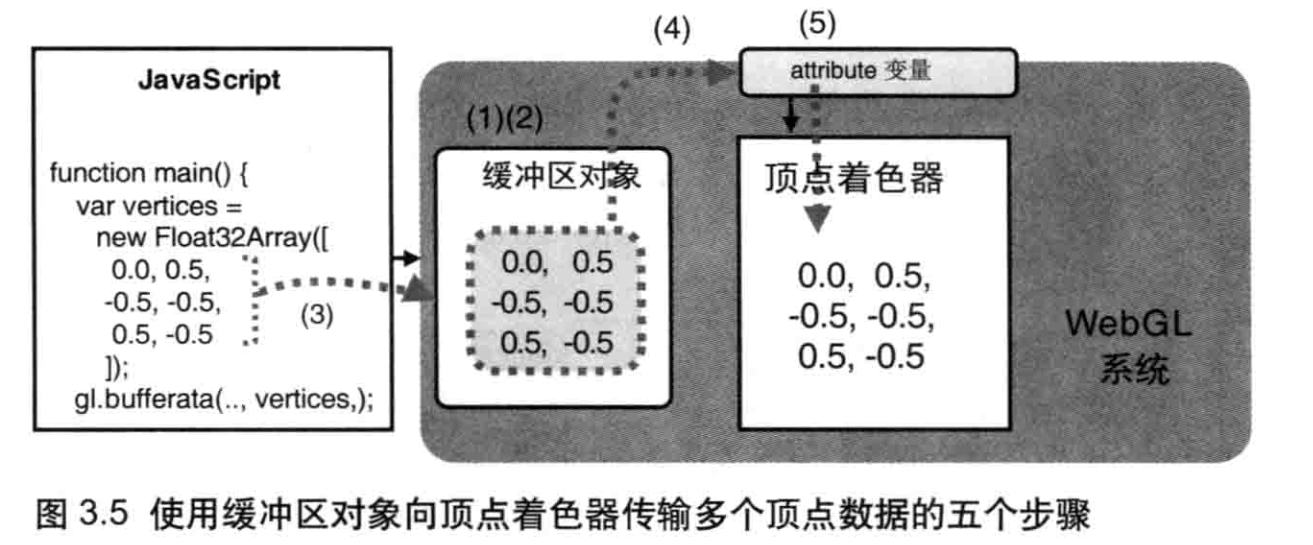
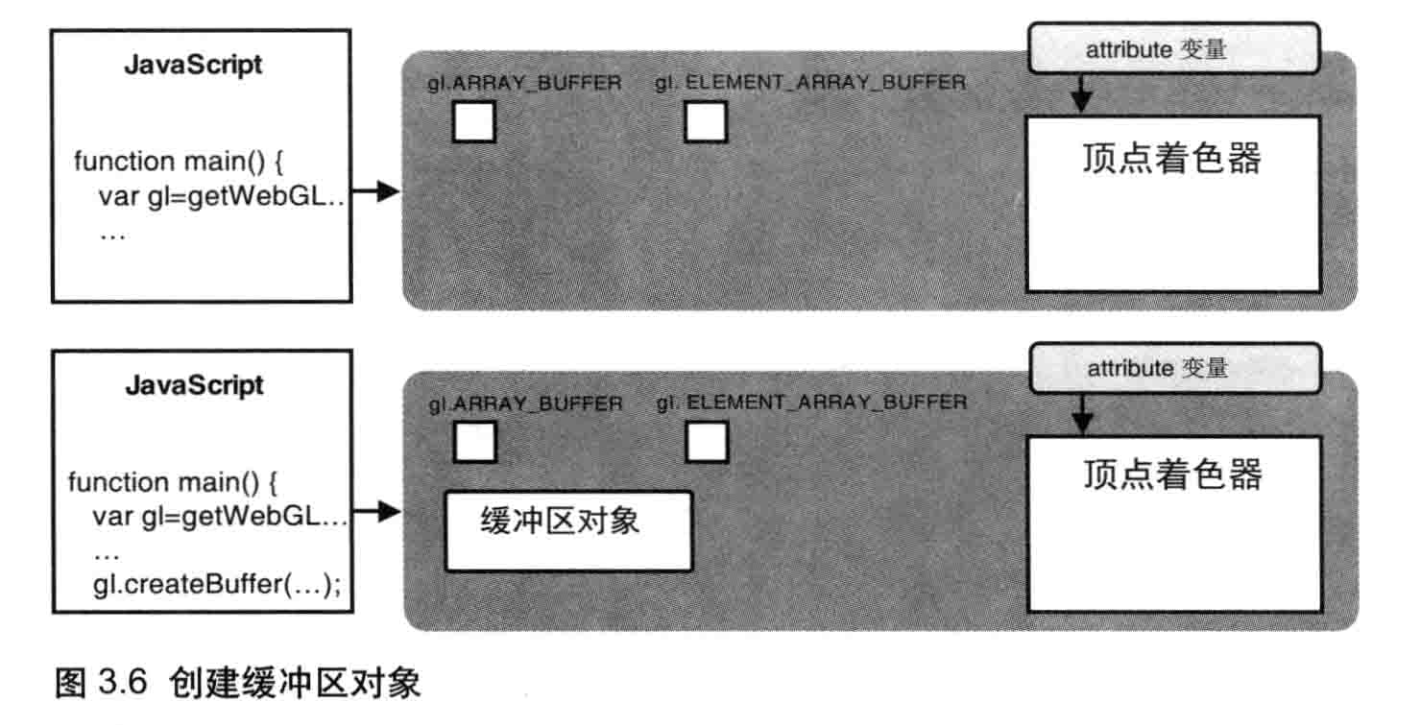
创建缓冲区对象（gl.createBuffer()）

使用WebGL时，你需要调用glcreateBuffer()方法来创建缓冲区对象。图3.6示意了该方法执行前后WebGL系统的中间状态，上面一张图是执行前的状态，下面一张图是执行后的状态。执行该方法的结果就是，WebGL系统中多了一个新创建出来的缓冲区对象。

下面是glcreateBuffer()的函数规范。

相应地，gl.deleteBuffer( buffer )函数可月用来删除被 glcreateBuffer() 创建出来的缓冲区对象。

绑定缓冲区（gl.bindBuffer()）

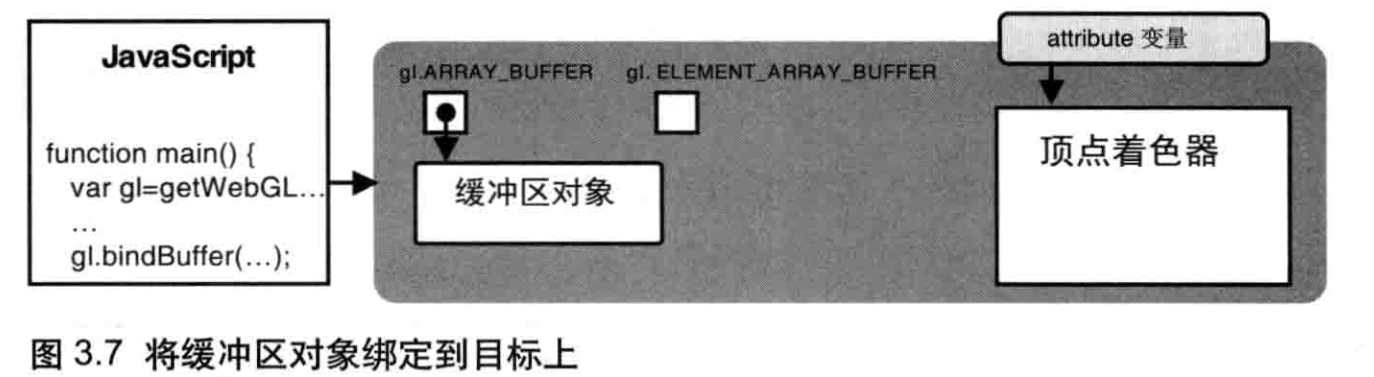
创建缓冲区之后的第2个步骤就是将缓冲区对象绑定到 WebGL 系统中已经存在的“目标”(target) 上。这这个“目标”表示缓冲区对象白的用途(在这里，就是向顶点着色器提供传给 attribute 变量的数据)，这样 WebGL 才能够够正确处理其中的内容。

我们将缓冲区对象绑定到了gl.ARRAY_BUFFER目标上，缓冲区对象中存储着的关于顶点的数据(顶点的位置坐标)。绑定后，WebGL系统内部状态发生了改变，如图3.7所示。

向缓冲区对象中写入数据（ gl.bufferData() ）

开辟空间并向缓冲区中写人数据。我们使用gl.bufferData()方法来完成这一步

该方法的效果是，将第2个参数vertices中的数据写入了绑定到第1个参数g1.ARRAY_BUFFER上的缓冲区对象。我们不能直接回缓冲区写人数据，而只能向“目标写入数据，所以要向缓冲区写数据，必须先绑定。该方法执行之后，WebGL系统的内部状态如图3.8所示。

现在我们来看看 gl.bufferData() 方法向缓冲中区中传入了什么数据。该方法使用了一个特殊的数组vertices将数据信专给顶点着色器。我们使用new运算符，并以<第一个顶点的x坐标和y坐标><第二个顶点的x坐标和y坐标>,等等的形式创建这个数组。

如你所见，我们使用了Float32Array对象，而不是JavaScript中更常见的Array对象。这是因为，JavaScript 中通用的数组 Array是一种通用的类型，既可以在里面存储数字也可以存储字符串，而并没有对“大量元素都是同一种类型”这种情况兄(比如vertices)进行优化。为了解决这个问题，WebGL引入了类型化数组，Float32Array就是其中之一。

类型化数组

为了绘制三维图形，WebGL通常需要同时处理大量相同类型的数据，例如顶点的坐标和颜色数据。为了优化性能，WebGL为每种基本数据类型引入了一种特殊的数组(类型化数组)。浏览器事先知道数组中的数据类型，所以处理起来也更加有效率。

例子中的Float32Array就是一种类型化数组组，通常用来存储顶点的坐标或颜色数据。应当牢记，WebGL中的很多操作都要用到类型化数组，比如gl.bufferData()中的第2个参数data。

与JavaScript中的Array数组相似，类型化数组也有一系列方法和属性(包括一个常量属性)，如表 3.2 所示。注意，与普通的 Array 数组不同，类型化数组不支持 push()和pop () 方法。

和普通的数组一样，类型化数组可以通过new运算符调用构造函数并传入数据而被创造出来。比如，为了创建Float32Array类型的顶点数据，你可以向构造函数中传入普通数组[0.0，0.5，-05，-0.5，0.5，-0.5]，这个数组表示一些顶点的数据。注意，创建类型化数组的唯一方法就是使用 new 运算符，不能使用 [] 运算符(那样创建的就是普通数组)。

此外，你也可以通过指定数组元素的个数来创建一个空的类型化数组

 var vertices = new Float32Array(4);

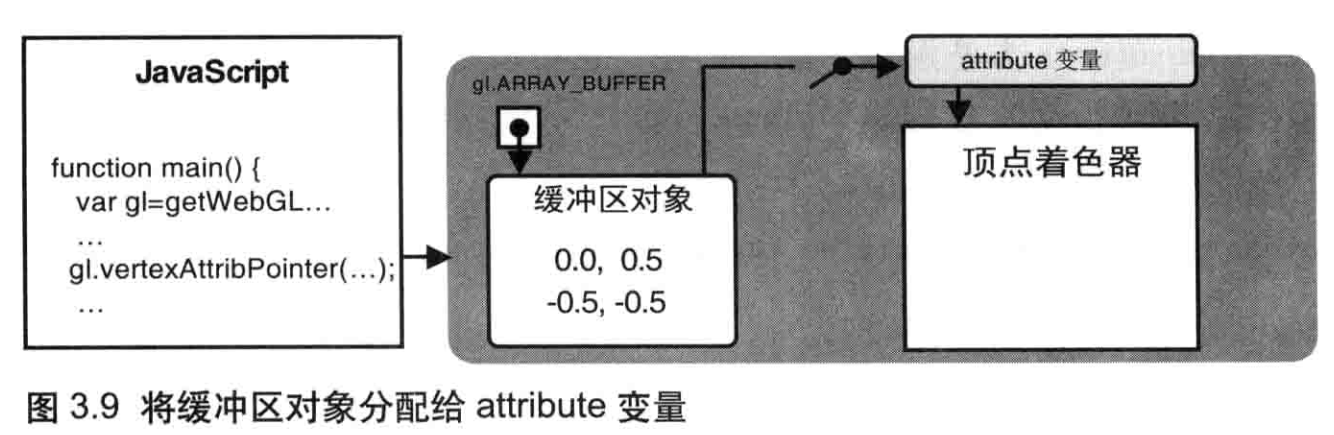
将缓冲区对象分配给attribute 变量（gl.vertexAttribPointer()）

如第2章所述你可以使用 gl.vertexAttrib[1234]f系列函数为 attribute 变量分配值。但是，这些方法一次只能向 attribute 变量分配(传输)一个值。而现在，你需要将整个数组中的所有值-- 这里是顶点数据- - 一次性地分配给一个 attribute 变量。

gl.vertexAttribPointer()方法解决了这个问是题它可以将整个缓冲区对象(实际上是缓冲区对象的引用或指针)分配给 attribute 变量。示例程序将缓冲区对象分配给attribute 变量a_Position。

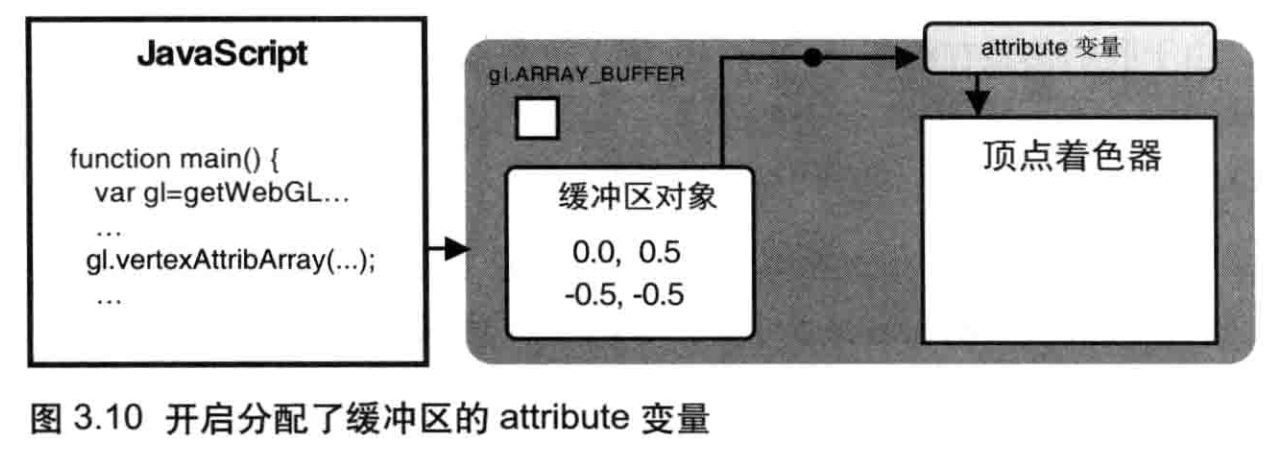
将整个缓冲区对象分配给了attribute变量，为WebGL绘图进行的准备工作就差最后一步了：进行最后的“开启”，使这次分配真正生效，如图 3.9 所示。

开启attribute 变量（ gl.enableVertexAttribArray() ）

为了使顶点着色器能够访问缓冲区内的数据，我们需要使用gl.enableVertexAttribArray()方法来开启attribute变量。

注意，虽然函数的名称似乎表示该函数是用来处理“顶点数组”的，但实际上它处理的对象是缓冲区。这是由于历史原因(从OpenGL中继承)造成的。

当你执行gl.enableVertexAttribArray() 并传人一个已经分配好缓冲区的 attribue 变量后，我们就开启了该变量，也就是说，缓冲区对象和 attribute 变量之间的连接就真正建立起来了，如图3.10所示。

同样，你可以使用gl.disableVertexAttribArray()来关闭分配。

现在，你只需要让顶点着色器运行起来，它会自动将缓冲区中的顶点画出来。如第2章，你使用gl.drawArrays()方法去绘制了一个点，现在你要画多个点，所用的仍然是gldrawArrays()方法，但是用的是方法法中的第2个和第3个参数。

注意，开启 attribute 变量后，你就不能再用 g1.vertexAttrib[1234]f()向它传数据了，除非你显式地关闭该 attribute 变量。实际上，你无法(也不应该)同时使用这两个函数。

gl.drawArrays() 的第2 个和第3 个参数

47 gl.drawArrays(gl.POINTS, 0, n);   // n 为3

由于我们仍然在绘制单个的点，第1个参数mode仍然是g1.POINTS；设置第2个参数first为0，表示从缓冲区中的第1个坐标开始画起；设置第3个参数count为3，表示我们准备绘制3个点(，n为为3)。

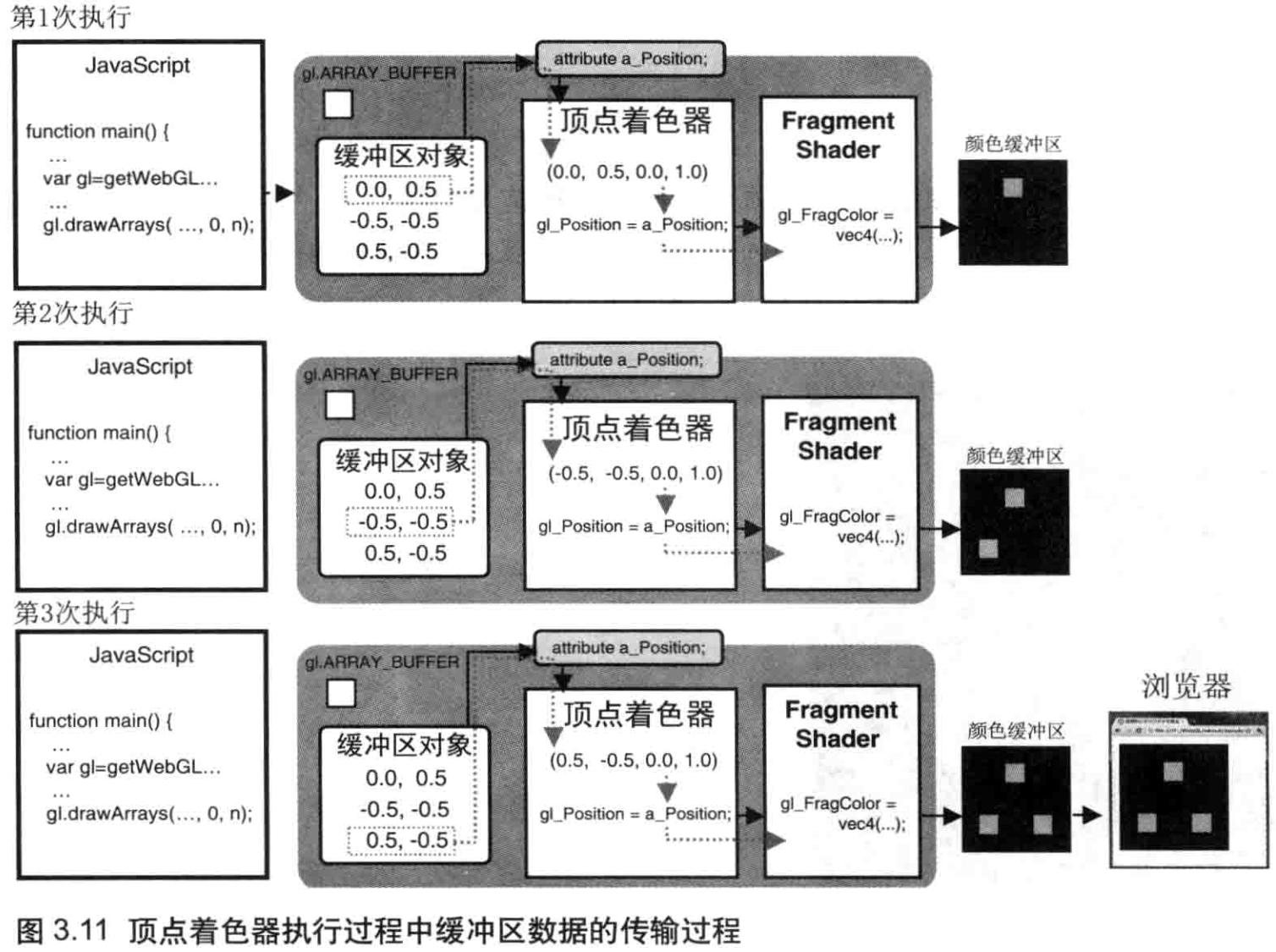
当程序运行到第47行时，实际上顶点着色器执行了count(3)次，我们通过存储在缓冲区中的顶点坐标数据被依次传给attribute变量，如图3.11所示。

注意，每次执行顶点着色器，a_Position的z和w分量值都会自动被设为0.0或1.0，因为a_Position需要4个分量(vec4)，而你只提供了两个。

记住,g1.vertexAttribPointer()的第2个参数size被设为2。之前说过，这个参数表示缓冲区中每个顶点有几个分量值，在缓冲区中你只提供x坐标和y坐标，所以你将它设为2。

gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);

在绘出所有点后，颜色缓冲区中的内容(3 个红点如图 3.2 所示)就会自动显示在浏览器上，其过程如图 3.11 底部所示

Hello Triangle

尝试使用上面的顶点绘制一个真正的图形(而不是单个的点)。

// HelloTriangle.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'void main() {\n' +
  '  gl_Position = a_Position;\n' +
  '}\n'

// Fragment shader program
var FSHADER_SOURCE =
  'void main() {\n' + '  gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' + '}\n'

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl')

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas)
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL')
    return
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.')
    return
  }

  // Write the positions of vertices to a vertex shader
  var n = initVertexBuffers(gl)
  if (n < 0) {
    console.log('Failed to set the positions of the vertices')
    return
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0, 0, 0, 1)

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT)

  // Draw the rectangle
  gl.drawArrays(gl.LINE_LOOP, 0, n)
}

function initVertexBuffers(gl) {
  var vertices = new Float32Array([0, 0.5, -0.5, -0.5, 0.5, -0.5])
  var n = 3 // The number of vertices

  // Create a buffer object
  var vertexBuffer = gl.createBuffer()
  if (!vertexBuffer) {
    console.log('Failed to create the buffer object')
    return -1
  }

  // Bind the buffer object to target
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer)
  // Write date into the buffer object
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW)

  var a_Position = gl.getAttribLocation(gl.program, 'a_Position')
  if (a_Position < 0) {
    console.log('Failed to get the storage location of a_Position')
    return -1
  }
  // Assign the buffer object to a_Position variable
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0)

  // Enable the assignment to a_Position variable
  gl.enableVertexAttribArray(a_Position)

  return n
}

与MultiPoint.js相比，两处关键的改动在于:

在顶点着色器中，指定点的尺寸的一行gl.Pointsize=10.0;被删去了。该语句只有在绘制单个点的时候才起作用。

gl.drawArrays()方法的第1个参数从gl.POINTS被改为了gl.TRIANGLES。

gl.drawArrays()的第1个参数mode十分强大。在这个参数上指定不同的值，我们可以按照不同的规则绘制图形。

基本图形

将gl.drawArrays()方法的第1个参数mode改为g1.TRIANGLES，就相当于告诉WebGL，“从缓冲区中的第1个顶点开始，使顶点着色器执行3次(n为3)，用这3个点绘制出一个三角形”;

这样，缓冲区的3个点就不再是相互独立的，而是同一个三角形中的3个顶点。

WebGL方法gl.drawArrays()既强大又灵活，这通过给第1个参数指定不同的值，我们就能以7种不同的方式来绘制图形。表3.3对此进行了详细介绍，其中v0、v1、v2等等表示缓冲区中的顶点，顶点的顺序将影响绘制的结果。

表3.3中的7种基本图形是WebGL可以直接绘制的图形，但是它们是WebGL绘制其他更加复杂的图形的基础。

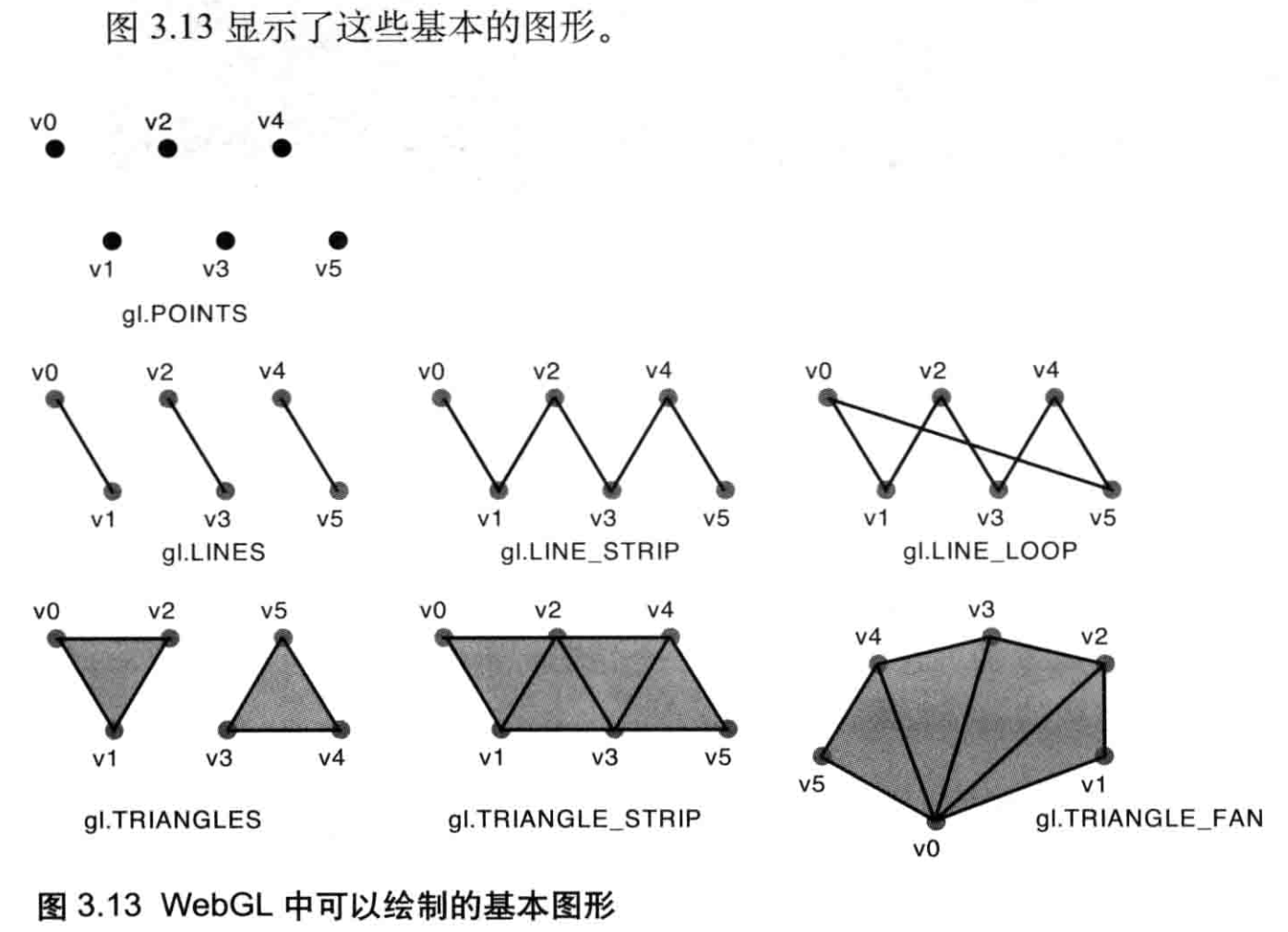
如图所示，WebGL只能绘制三种图形:点、线段和三角形。但是，正如本章开头所说到的，从球体到立方体，再到游戏中的三维角色，都可以由小的三角形组成。实际上，你可以使用以上这些最基本的图形来绘制出任何东西。

Hello Rectangle（HelloQuad）

// HelloQuad.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'void main() {\n' +
  '  gl_Position = a_Position;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  'void main() {\n' +
  '  gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Write the positions of vertices to a vertex shader
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the positions of the vertices');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0, 0, 0, 1);

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);

  // Draw the rectangle
  gl.drawArrays(gl.TRIANGLE_STRIP, 0, n);
}

function initVertexBuffers(gl) {
  var vertices = new Float32Array([
    -0.5, 0.5,   -0.5, -0.5,   0.5, 0.5,　0.5, -0.5
  ]);
  var n = 4; // The number of vertices

  // Create a buffer object
  var vertexBuffer = gl.createBuffer();
  if (!vertexBuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // Bind the buffer object to target
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
  // Write date into the buffer object
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);

  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if (a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  // Assign the buffer object to a_Position variable
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);

  // Enable the assignment to a_Position variable
  gl.enableVertexAttribArray(a_Position);

  return n;
}

我们使用这个最基本的方法来试着绘制一个矩形。示例程序名为HelloQuad，图3.16 显示了矩形的顶点。当然，顶点的个数为4，因为这是一个矩形。

如上一节所述，WebGL不能直接绘制矩形，你需要将其划分为两个三角形(v0，v1，v2)和(v2,v1,v3)，然后通过gl.TRIANGLES，gl.TRIANGLES_STRIP，或者gl.TRIANGLES_FAN 将其绘制出来。本例使用gl.TRIANGLES_STRIP进行绘制，只需要用到4个顶点。如果用g1.TRIANGLES，就需要用到6个。

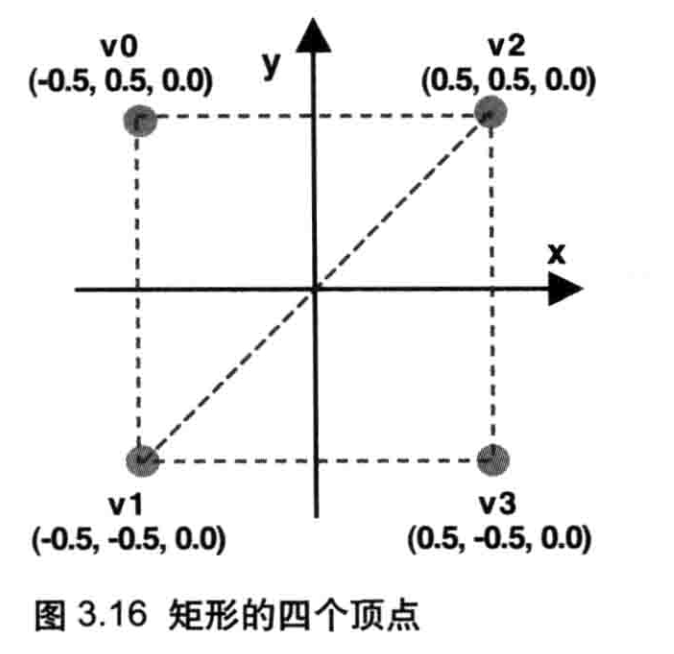
注意顶点的顺序，否则不能正确绘图。

因为新添了一个顶点，所以还需要将顶点的个数n从3改成4。

移动、旋转和缩放

现在，你已经掌握了绘制图形(如三角形和矩开彭)的方法。让我们更进一步，尝试移动(平移)、旋转和缩放三角形，然后在屏幕上
绘制出来。这样的操作称为变换(transformations)或仿射变换(affinetransformations)。

平移

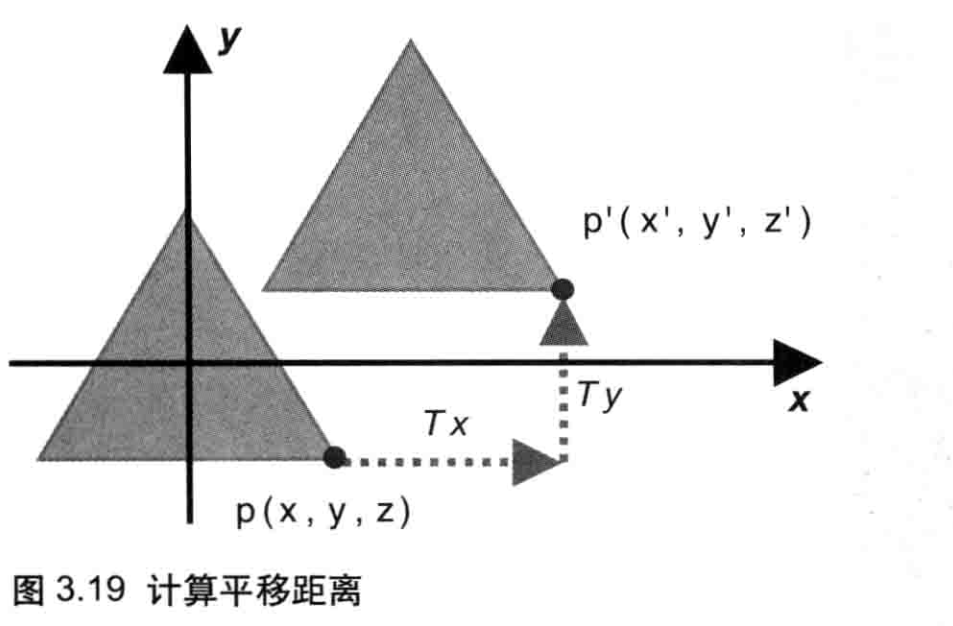
考虑一下，为了平移一个三角形，你需要对它的每一个顶点做怎样的操作?答案是，你需要对顶点坐标的每个分量(x和y)，加上三角形在对应轴(如X轴或Y轴)上平移的距离。比如，将点p(x，y,z)平移到 p'(x',y',z')，在X轴、Y轴、z轴三个方向上平移的距离分别为Tx，Ty，Tz，其中Tz为0，如图3.19所示。

那么在坐标的对应分量上，直接加上这些T值，就可以确定p的坐标了，如等式3.1所示。

我们只需要着色器中为顶点坐标的每个分量加上一个常量就可以实现上面的等式。显然，这是一个逐顶点操作(per-vertexoperation)而非逐片元操作，上述修改应当发生在顶点着色器，而不是片元着色器中。

一旦你理解了这一点，修改代码就很简单了:"将平移距离Tx、Ty、Tz的值传入顶点着色器，然后分别加在顶点坐标的对应分量上，再贴武值给gl_Position。下面看看修改后的示例程序。

// TranslatedTriangle.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'uniform vec4 u_Translation;\n' +
  'void main() {\n' +
  '  gl_Position = a_Position + u_Translation;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  'void main() {\n' +
  '  gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' +
  '}\n';

// x y z三个方向的平移距离
var Tx = 0.5, Ty = 0.5, Tz = 0.0;

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Write the positions of vertices to a vertex shader
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the positions of the vertices');
    return;
  }

  // 传递平移距离给顶点着色器
  var u_Translation = gl.getUniformLocation(gl.program, 'u_Translation');
  if (!u_Translation) {
    console.log('Failed to get the storage location of u_Translation');
    return;
  }
  gl.uniform4f(u_Translation, Tx, Ty, Tz, 0.0);

  // Specify the color for clearing <canvas>
  gl.clearColor(0, 0, 0, 1);

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);

  // Draw the rectangle
  gl.drawArrays(gl.TRIANGLES, 0, n);
}

function initVertexBuffers(gl) {
  var vertices = new Float32Array([
    0, 0.5,   -0.5, -0.5,   0.5, -0.5
  ]);
  var n = 3; // The number of vertices

  // Create a buffer object
  var vertexBuffer = gl.createBuffer();
  if (!vertexBuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // Bind the buffer object to target
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
  // Write date into the buffer object
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);

  // Assign the buffer object to the attribute variable
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if (a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);

  // Enable the assignment to a_Position variable
  gl.enableVertexAttribArray(a_Position);

  return n;
}

因为Tx、Ty、Tz对于所有顶点来说是固定(一致)的，所以我们使用uniform变量u_Translation来表示三角形的平移距离。首先，获取uniform变量的存储位置，然后将数据传给着色器

注意，gl.uniform4f()函数需接收齐次坐标，所以我们把最后一个参数被设为0.0。

如你所见，我们新定义了uniform变量u_Translation，用来接收了三角形在各轴方向上的平移距离。该变量的类型是vec4，这样它就可以与vec4类型的顶点坐标aPosition直接相加，然后赋值给同样是vec4类型的gl_Position。记住，第2章中讲过，GLSL ES 中的赋值操作只能发生在相同类型的变量之间。

在顶点着色器中，按照等式3.1，为a_Position变量的每个分量(xy,z)加上u_Translaation变量中对应方向的平移距离(Tx，Ty，Tz)，并赋值给gl_Position。

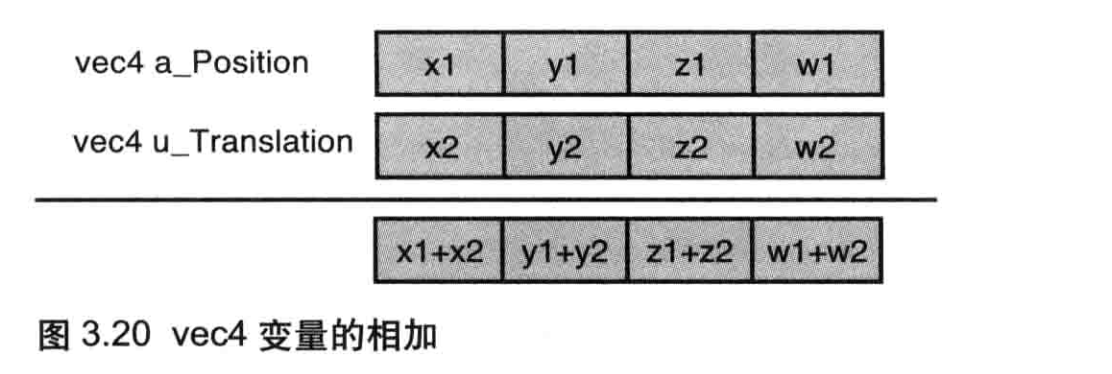
因为a_Position和u_Translation变量都是vec4类型的，所以你可以直接使用+号，两个的矢量的对应分量会被同时相加，如图3.20所示方便的矢量相加运算是GLSLES提供的特性之一，我们将在第6章更详细地讨论GLSL ES.

最后，我来解释一下齐次坐标矢量的最后一个分量w。如第2章所述，gl_Position是齐次坐标，具有4个分量。如果齐次坐标的最后一个分量是1.0，那么它的前三个分量就可以表示一个点的三维坐标。在本例中，如图3.20所示，平移后点坐标第4分量w1+w2必须是1.0(因为点的位置坐标平移之后还是一个点位置坐标)，而w1是1.0(它是平移前点坐标第4分量)，所以平移矢量本身的第4分量w2只能是0.0，这就是为什么gl.uniform4f()的最后一个参数为0.0**。

最后，调用gl.drawArrays(g1TRIANGLES，0，n)执行顶点着色器(第58行)，每次执行都会进行以下3步：

将顶点坐标传给a_Position;

向a_Position加上u_Translation;

结果赋值给gl_Position。

旋转

旋转比平移稍微复杂一些，因为描述一个旋转本身就比描述一个平移复杂。为了描述一个旋转，你必须指明:

旋转轴(图形将围绕旋转轴旋转)。

旋转方向(方向:顺时针或逆时针)。

旋转角度(图形旋转经过的角度)。

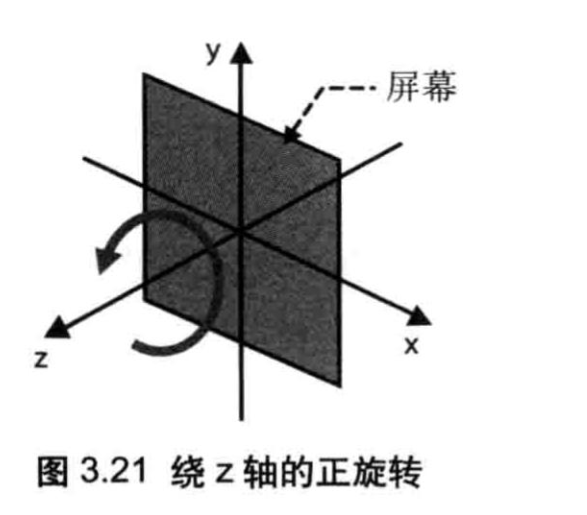
在本节中我们这样来表述旋转操作:绕Z轴，逆时针旋转了β角度。这种表述方式同样适用于绕X轴和Y轴的情况。

在旋转中，关于“逆时针”的约定是:如果 β是正值，观察者在Z轴正半轴某处，视线沿着Z轴负方向进行观察，那么看到的物体就是逆时针旋转的，如图 3.21 所示。这种情况又可称作正旋转(positiverotation)**。我们也也可以使用右手来确认旋转方向(正如右手坐标系一样):右手握拳，大拇指伸直并使其指向旋转轴的正方向，那么右手其余几个手指就指明了旋转的方向，因此正旋转又口可以称为右手法则旋转(right-hand-rulerotation)。在第2章中说过，右手法则旋转是本书中WebGL程序的默认设定。

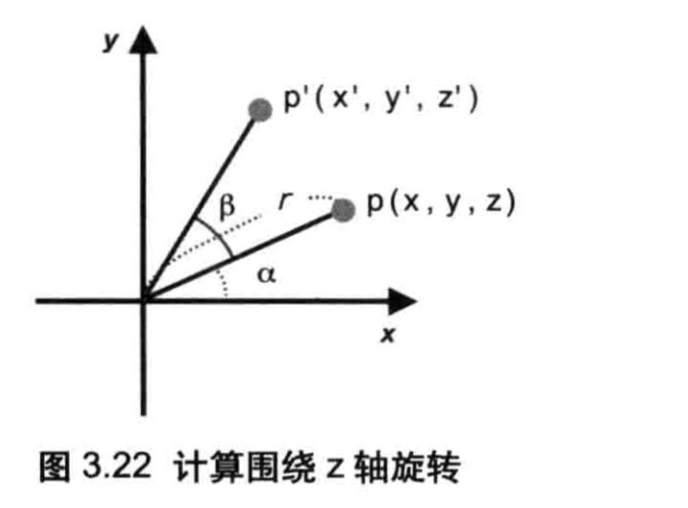
根据图3.22，假设点p(xyz)旋转β角度之后变为了点p'(x'，y'，z'):首先旋转是绕Z轴进行的，所以z坐标不会变，可以直接忽略;然后，x坐标和y生坐标的情况有一些复杂。

在图3.22中，r是从原点到点p的距离，而a是X轴旋转到点p的角度。用这两个变量计算出点p的坐标，如等式3.2所示。

我们可以把sinβ和cosβ的值传给顶点着色器，然后在着色器中根据等式3.3计算旋转后的点坐标，就可以实现旋转这个点的效果了。使用JavaScript内置的Math对象的sin()和cos()方法来进行三角函数运算

// RotatedTriangle.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  // x' = x cosβ - y sinβ
  // y' = x sinβ + y cosβ　Equation 3.3
  // z' = z
  'attribute vec4 a_Position;\n' +
  'uniform float u_CosB, u_SinB;\n' +
  'void main() {\n' +
  '  gl_Position.x = a_Position.x * u_CosB - a_Position.y * u_SinB;\n' +
  '  gl_Position.y = a_Position.x * u_SinB + a_Position.y * u_CosB;\n' +
  '  gl_Position.z = a_Position.z;\n' +
  '  gl_Position.w = 1.0;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  'void main() {\n' +
  '  gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' +
  '}\n';

// 旋转角度
var ANGLE = 90.0; 

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Write the positions of vertices to a vertex shader
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the positions of the vertices');
    return;
  }

  // 将旋转图形所需的数据传输给顶点着色器
  var radian = Math.PI * ANGLE / 180.0; // 转为弧度制
  var cosB = Math.cos(radian);
  var sinB = Math.sin(radian);

  var u_CosB = gl.getUniformLocation(gl.program, 'u_CosB');
  var u_SinB = gl.getUniformLocation(gl.program, 'u_SinB');
  if (!u_CosB || !u_SinB) {
    console.log('Failed to get the storage location of u_CosB or u_SinB');
    return;
  }
  gl.uniform1f(u_CosB, cosB);
  gl.uniform1f(u_SinB, sinB);

  // Specify the color for clearing <canvas>
  gl.clearColor(0, 0, 0, 1);

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);

  // Draw the rectangle
  gl.drawArrays(gl.TRIANGLES, 0, n);
}

function initVertexBuffers(gl) {
  var vertices = new Float32Array([
    0, 0.5,   -0.5, -0.5,   0.5, -0.5
  ]);
  var n = 3; // The number of vertices

  // Create a buffer object
  var vertexBuffer = gl.createBuffer();
  if (!vertexBuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // Bind the buffer object to target
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
  // Write date into the buffer object
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);

  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if (a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  // Assign the buffer object to a_Position variable
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);

  // Enable the assignment to a_Position variable
  gl.enableVertexAttribArray(a_Position);

  return n;
}

由于目的是为了将三角形旋转90度，我们得事先计算90度的正弦值和余弦值。在JavaScript中算出这两个值，再传给顶点着色器的两个uniform变量。

你也可以将旋转的角度传人顶点着色器，并在着色器中计算正弦值和余弦值。但是，实际上所有顶点旋转的角度都是一样的，在JavaScript中算好正弦值和余弦值，然后再传递进去，只需要计算一次，效率更高。

按照本书的命名约定，两个uniform变量分别为uCosB和usinB。再次提醒，之所以使用uniform变量，是因为这两个变量的值与顶点无关。

之前进行平移变换时，齐次坐标的x、y、z、w分量是作为整体进行加法运算的;而进行旋转变换时，为了计算等式33，需要单独访问a_Position的每个分量。我们使用点操作符“.”来访问分量，如a_Position.x，a_Position.y或a_Position.z(如图324所示，参见第6章)。

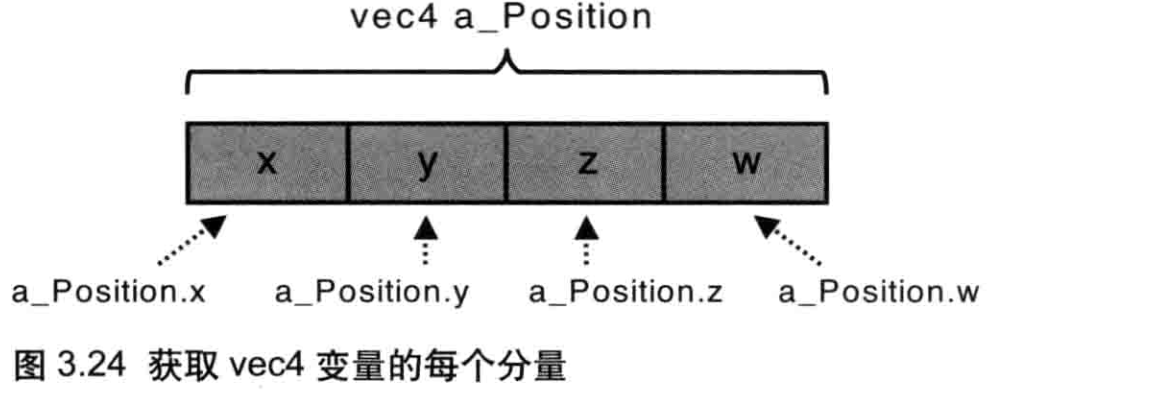
根据等式3.3，还需要将z原封不动地赋给z'，以及将最后一个w分量设为1.0。

本例向顶点着色器传入了cosβ和sinβ值(而非平移距离Tx等)。我们使用JavaScript内置的Mathsin()和Math.cos()函数来计算ß的正弦和余弦值。但是，这两个方法必须接受弧度制(而不是角度制)的参数，所以我们还得先把β值从角度制转为弧度制:将角度值90乘以π然后除以180，访问Math.PI可以获得π的值。

在浏览器中运行程序，可见屏幕上的三角形逆时针旋转了90度;如果指定了一个负的角度值，三角形就会顺时针旋转。不论旋转方向如何，等式3.3都是通用的，如果要顺时针旋转90度的话，直接将角度赋值为-90即可，数学sin()和数学cos()将自动为你处理剩下的事情。

变换矩阵：旋转

对于简单的变换，你可以使用数学表达式来实现。但是当情形逐渐变得复杂时，你很快就会发现利用表达式运算实际上相当繁琐。比如，图3.25显示了一个“旋转后平移”的过程，如果使用数学表达式，我们就需要等式3.1和等式3.3叠加，获得一个新的等式，然后在顶点着色器中实现。

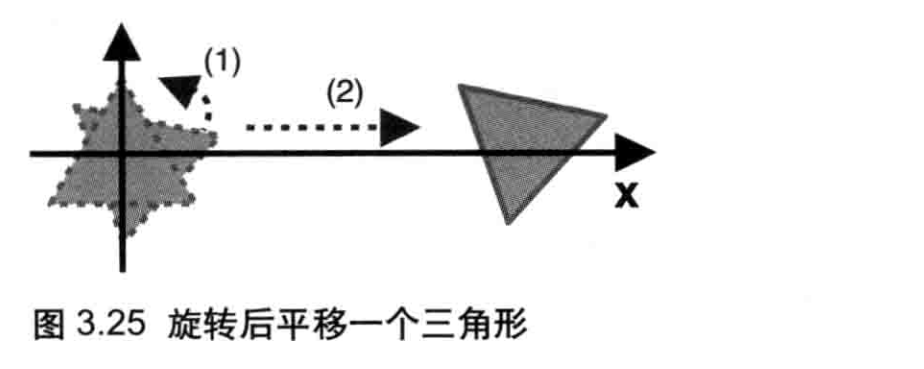
但是如果这样做，每次都需要进行一次新的变换，我们就需要重新求取一个新的等式，然后实现一个新的着色器，这当然很不科学。好子在我们可以使用另一个数学工具-变换矩阵(Transformationmatrix)来完成这项工作。变换矩阵非常适合操作计算机图形。

如图3.26所示，矩阵是一个矩形的二维数组，数字按照行(水平方向)和列(垂直方向)排列，数字两侧的方括号表示这些数字是一个整体一个矩阵)。我们将使用矩阵来表示前面的计算过程。

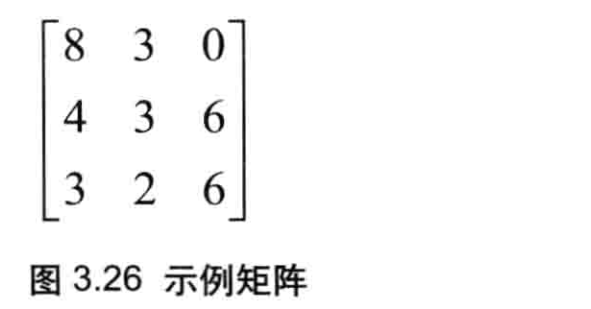
在解释如何使用变换矩阵来替代数学表达式之前，你需要理解矩阵和矢量的乘法。矢量就是由多个分量组成的对象，比如顶点的坐标(0.0,0.5,1.0)。

矩阵和矢量的乘法可以写成等式34的形式(虽然乘号“x”通常被忽略不写，但是为了强调，本书中我们总是明确地将这个符号写号出来)。可见，将矩阵(中间)和矢量(右边)相乘,就获得了一个新的矢量(左边)。注意矩阵的乘法不符合交换律也就是说AxB和BxA并不相等。第6章将更深入地讨论这些问题。

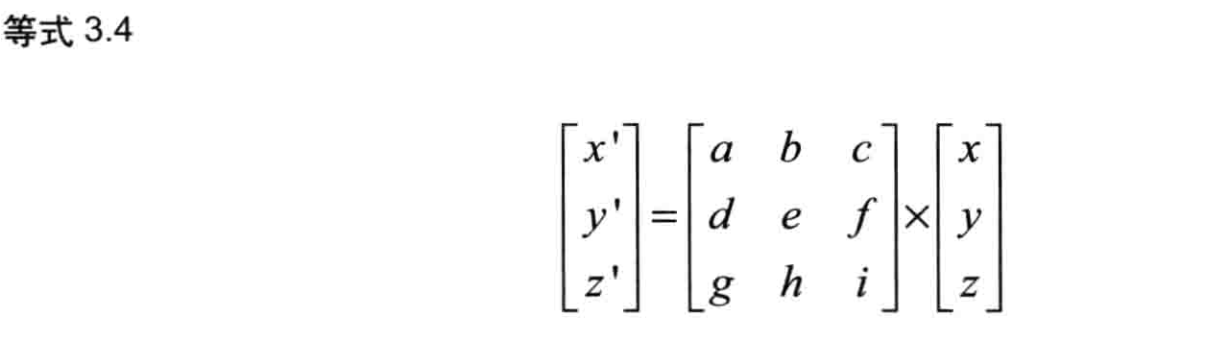
上式中的这个矩阵具有3行3列，因此又被称为3x3矩阵。矩阵右侧是一个由x、y、z组成的矢量(为了与矢量相乘，矢量被写成列的的形式，其仍然表示点的坐标)。矢量具有3个分量，因此被称为三维矢量。再次说明，数字两侧的方括号表示这些数字是一个整体(一个矢量)。**

在本例中，矩阵与矢量相乘得到的新矢量，其三个分量为x、y、z，其值如等式3.5所示。注意，只有在矩阵的列数与矢量的行数相等时才可以将两者相乘。

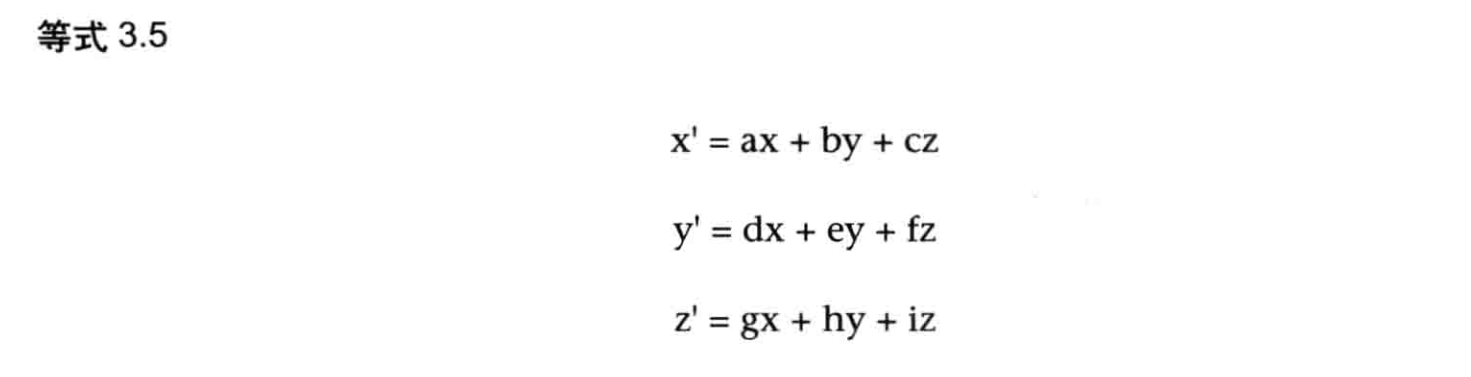
这个矩阵就被称为变换矩阵(transformationmatrix),因为它将右侧的矢量(x,y,z)“变换”为了左侧的矢量(x',y',z')。上面这个变换矩阵进行的变换是一次旋转，所以这个矩阵又可以被称为旋转矩阵(rotationmatrix)。

可以看到，等式3.7中矩阵的元素都是等式3.6中的系数。一旦你熟悉这种矩阵表示法，进行变换就变得非常简单了。如果你不熟悉，你应当花点时间好好地理解它，变换矩阵的概念在三维图形学中非常重要。

变换矩阵在三维计算机图形学中应用得如此广法，以致于着色器本身就实现了矩阵和矢量相乘的功能。

变换矩阵：平移

比较一下等式3.5和等式3.1(平移的数学表达式)，如下所示:

这里第二个等式的右侧有常量项Tx，第一个等式中没有，这意味着我们无法通过使用一个3x3的矩阵来表示平移。为了解决这个问是题，我们可以使用一个4x4的矩阵，以及具有第4个分量(通常被设为1.0)的矢量。也就是说，我们假设点p的坐标为(x，y，z，1)，平移之后的点p'的坐标为(x'，y，z，1)，如等式3.8所示:

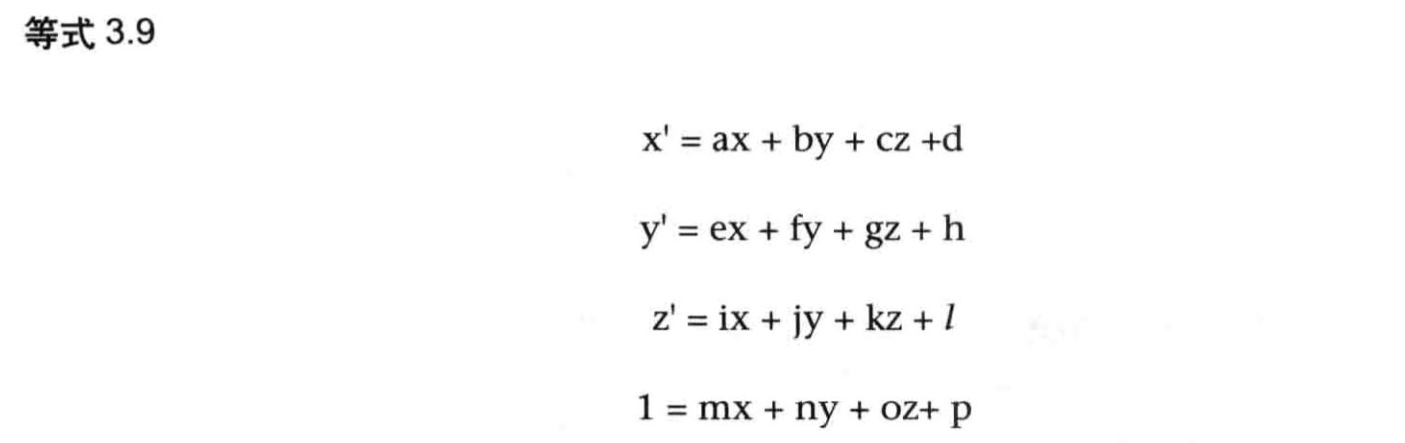
根据最后一个式子1=mx+ny+oz+p，很容易求算出系数m=0，n=0，o=0，p=1。这些方程都有常数项d、h、l和p，看上去比较适合等式3.1(因为等式3.1中也有常数项)。等式3.1(平移)如下所示，我们将它与等式3.9进行比较:

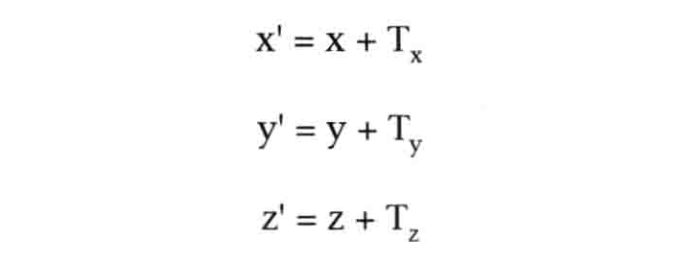
比较x'，可知a=1，b=0，c=0，d=Tx;类似地，比较y'，可知e=0，f=1，g=0，h=Ty;比较z'，可知i=0，j=0，k=1，1=Tz。这样，你就可以写出表示平移的矩阵，又称为平移矩阵(translationmatrix)，如等式3.10所示

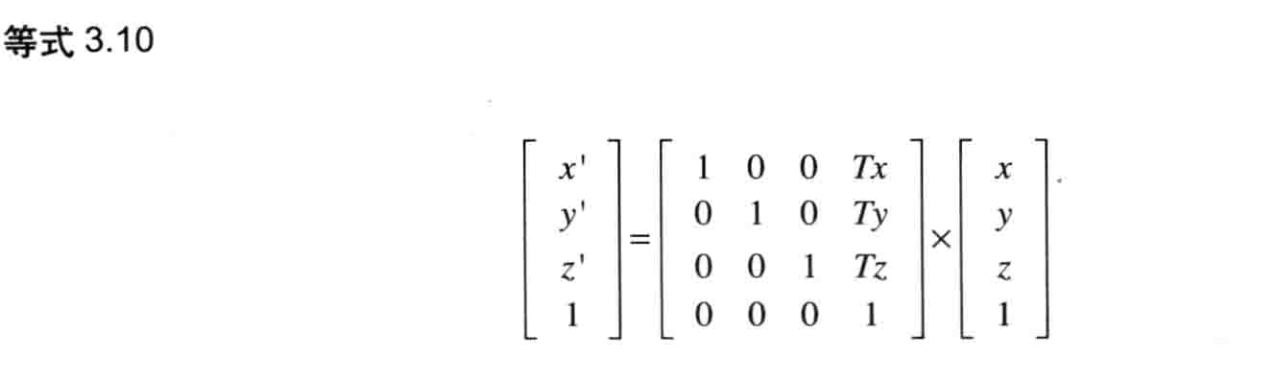
4x4的旋转矩阵

至此，我们已经成功地创建了一个旋转矩阵和一个平移矩阵，这两个矩阵的作用与此前示例程序中的数学表达式的作用是一样的，那就是计算变换后的顶点坐标。在“先旋转再平移”的情形下，我们需要将两个矩阵组合起来(你应该记得，这也是我们使用矩阵的初衷)，然而旋转矩阵(3x3矩阵)与平移知矩阵(4x4矩阵)的阶数不同。我们不能把两个阶数不一样的矩阵组合起来，所以得使用某种手段，使这两个矩阵的阶数一致。

将旋转矩阵从一个3x3矩阵转变为一个4x4知矩阵，只需要将方程3.3和方程3.9比较一下即可。

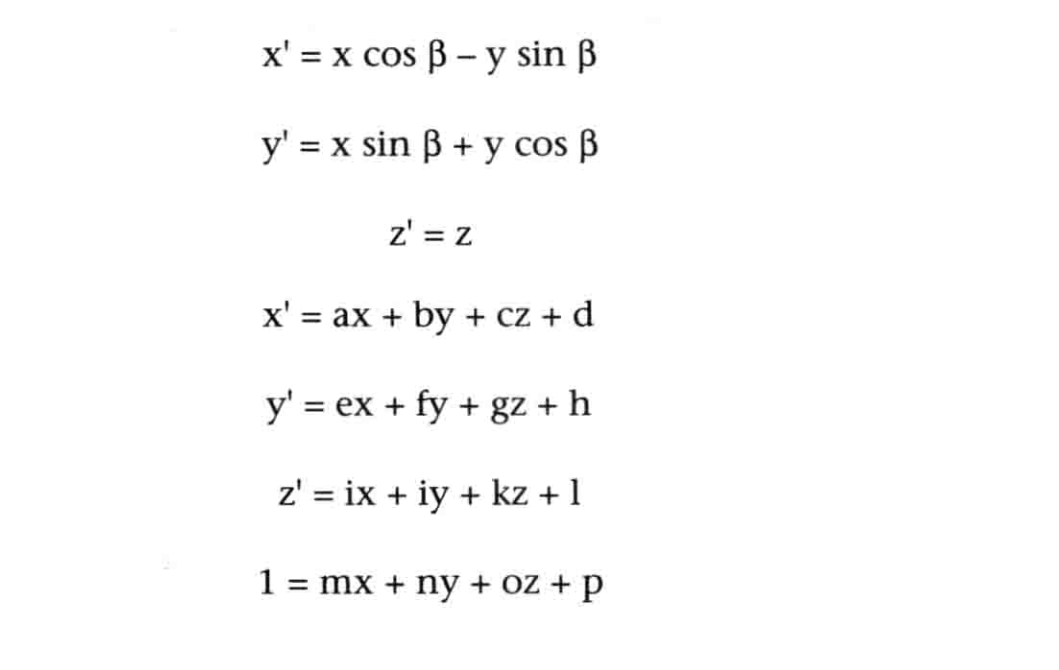
例如，当你通过比较x'=xcosβ-ysinβ与x'=ax+by+cz+d时，可知a=cosβ，b=-sinβ，c=0，d=0。以此类推，求得y'和z'等式中的系数，最终得到4x4的旋转矩阵，如等式3.11所示:

这样，我们就可以使用相同阶数(4x4)的矩阵来表示平移和旋转，实现了最初的目标!

示例程序（RotatedTriangle_Matrix.js 旋转矩阵）

// RotatedTriangle_Matrix.js (c) matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'uniform mat4 u_xformMatrix;\n' +
  'void main() {\n' +
  '  gl_Position = u_xformMatrix * a_Position;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  'void main() {\n' +
  '  gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' +
  '}\n';

// The rotation angle
var ANGLE = 90.0;

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }
 
  // Write the positions of vertices to a vertex shader
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the positions of the vertices');
    return;
  }

  //  创建旋转矩阵
  var radian = Math.PI * ANGLE / 180.0; // 角度值转弧度制
  var cosB = Math.cos(radian), sinB = Math.sin(radian);

  // 注意webgl中矩阵是列主序的
  var xformMatrix = new Float32Array([
     cosB, sinB, 0.0, 0.0,
    -sinB, cosB, 0.0, 0.0,
      0.0,  0.0, 1.0, 0.0,
      0.0,  0.0, 0.0, 1.0
  ]);

  // 将旋转矩阵传输给顶点着色器
  var u_xformMatrix = gl.getUniformLocation(gl.program, 'u_xformMatrix');
  if (!u_xformMatrix) {
    console.log('Failed to get the storage location of u_xformMatrix');
    return;
  }
  gl.uniformMatrix4fv(u_xformMatrix, false, xformMatrix);

  // Specify the color for clearing <canvas>
  gl.clearColor(0, 0, 0, 1);

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);

  // Draw the rectangle
  gl.drawArrays(gl.TRIANGLES, 0, n);
}

function initVertexBuffers(gl) {
  var vertices = new Float32Array([
    0, 0.5,   -0.5, -0.5,   0.5, -0.5
  ]);
  var n = 3; // The number of vertices

  // Create a buffer object
  var vertexBuffer = gl.createBuffer();
  if (!vertexBuffer) {
    console.log('Failed to create the buffer object');
    return false;
  }

  // Bind the buffer object to target
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
  // Write date into the buffer object
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);

  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if (a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  // Assign the buffer object to a_Position variable
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);

  // Enable the assignment to a_Position variable
  gl.enableVertexAttribArray(a_Position);

  return n;
}

u_xformMatrix变量表示等式3.11中的旋转矩阵，a_Position变量表示顶点的坐标(即等式 3.11中右侧的矢量)，二者相乘得到变换后的顶点坐标，与等式3.11中相同。

代码中完成矩阵与矢量相乘的运算(gl_Position=u_xformMatrix * a_Possition)。这时因为着色器内置了常用的矢量和矩阵运算功能，这种强大特性正是专为三维计算机图形学而设计的。

由于变换矩阵是4x4的，GLSLES需要知道每个变量的类型，所以我们将u_xformMatrix定义为mat4类型。如你所料，mat4类型的变量就是4x4的矩阵。

JavaScript按照等式3.11计算旋转矩阵，然后将其传给u_xformMatrix。

  //  创建旋转矩阵
  var radian = Math.PI * ANGLE / 180.0; // 角度值转弧度制
  var cosB = Math.cos(radian), sinB = Math.sin(radian);

  // 注意webgl中矩阵是列主序的
  var xformMatrix = new Float32Array([
     cosB, sinB, 0.0, 0.0,
    -sinB, cosB, 0.0, 0.0,
      0.0,  0.0, 1.0, 0.0,
      0.0,  0.0, 0.0, 1.0
  ]);

 //...
 gl.uniformMatrix4fv(u_xformMatrix, false, xformMatrix);

这段代码首先计算了90度的正弦值和余弦值，这两个值需要被用来构建旋转矩阵;之后创建了Float32Array类型的xformMatrix变量表示旋转矩阵(第48行)。与GLSLES不同，JavaScript并没有专门表示矩阵的类型，所以你需要使用类型化数组Float32Array。我们在数组中存储矩阵的每个元素，但问题是:矩阵是二维的，其元素按照行和列进行排列，而数组是一维的，其元素只是排成一行。这里，我们可以按照两种方式在数组中存储矩阵元素:按行主序(row major oder) 和按列主序 (columnmajor order)，如图3.27所示。

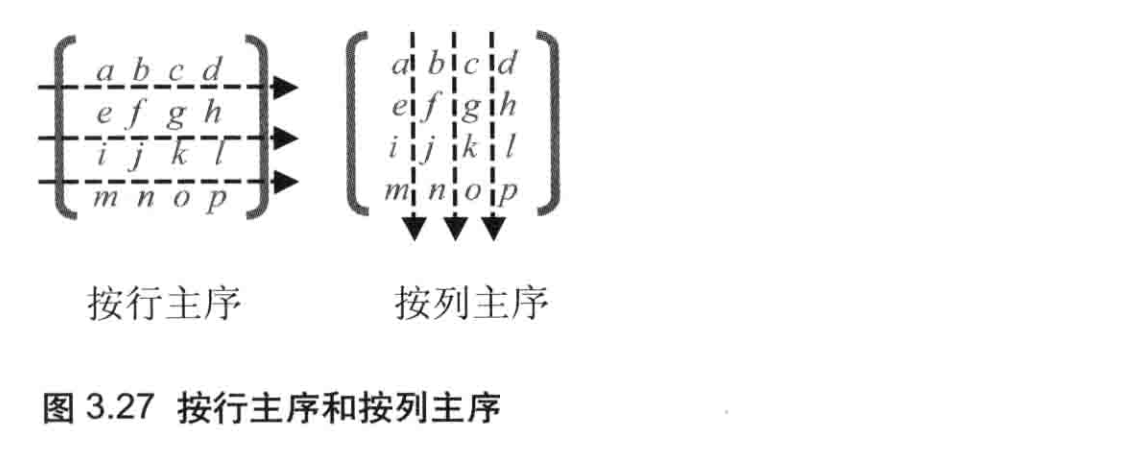
WebGL 和 OpenGL 一样，矩阵元素是按列主序存储在数组中的。比如，图3.27所示的矩阵存储在数组中就是这样的:[a,e,i,m,b,f,j,n,c,g,k,o,d,n,l,p]。本例中，旋转矩阵也是按照这样的顺序存储在Float32Array类型的的数组中的(第49~52行)。

最后，我们使用gl.uniformMatrix4fv()函数，将刚刚生成的数组传给uxformMatrix变量。注意,函数名的最后一个字母是v，表示它可以向着色器传输多个数据值。

平移：相同的策略

如你所见，4x4的矩阵不仅可以用来表示平移，也可以用来表示旋转。不管是平移还是旋转，你都使用如下形式来进行矩阵和矢量的运运算以完成变换：<新坐标>=<变换矩阵>*<旧坐标>，比如在着色器中:

  '  gl_Position = u_xformMatrix * a_Position;\n' +

这意味着，如果我们改变数组xformMatrix中的元素，使之成为一个平移矩阵，那么就可以实现平移操作，其效果就和之前使用数学表达式进行的平移操作一样(图3.18)。

因此，修改RotatedTriangle_Matrix.js，将放旋转角度修改为与平移相关的变量:

var Tx = 0.5, Ty = 0.5, Tz = 0.0

我们还需重写创建矩阵的代码，记住，矩阵是按列主序存储的。虽然xformMatrix现在是一个平移矩阵了，但我们仍使用这个变量名。因为对于着色器而言，旋转矩阵和平移矩阵其实是一回事。最后，你不会用到ANGLEA变量，把与旋转相关的代码注释掉

//创建旋转矩阵
//varradian=MathPI*ANGLE/1800;//角度值转弧度制
//var cosB=Mathcos(radian)，sinB=Mathsin(radian);

//注意:WebGL中矩阵是列主序的
var xformMatrix=newFloat32Array([
1.0，0.0，0.0，0.0,
0.0，1.0，0.0，0.0，
0.0,0.0，1.0，0.0,
Tx，Ty，Tz，1.0
]);

变化矩阵：缩放

仍然假设最初的点p，经过缩放操作之后变成了p'。

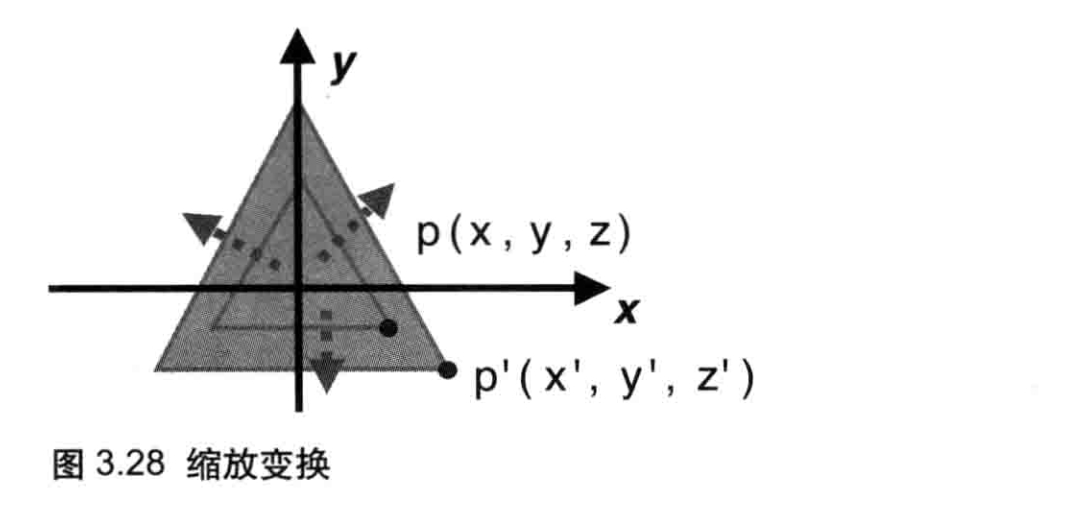
假设在三个方向X轴，Y轴，Z轴的缩放因子Sx，Sy，Sz，不相关，那么有:

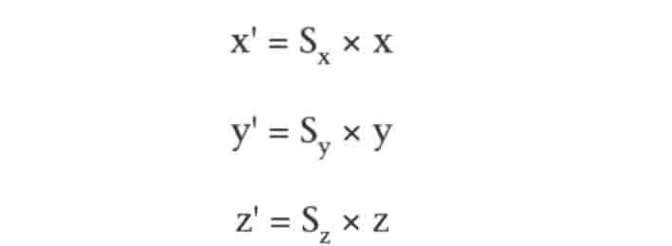
将上式与等式3.9作比较，可知缩放操作的变换矩阵:

和之前的例子一样，我们只要将缩放矩阵传给xformMatrix变量。下面这个示例程序会将三角形在垂直方向上拉伸到1.5倍。

varSx=10，Sy=15，Sz=10;
...
//注意:WebGL中矩阵是列主序的
var xformMatrix=newFloat32Array([
Sx，0.0，0.0，0.0,
0.0，Sy，0.0，0.0，
0.0，0.0，Sz，0.0，
0.0，0.0，0.0，1.0
]

注意，如果将Sx、Sy或Sz指定为0，缩放因子就就是0.0，图形就会缩小到不可见。如果希望保持图形的尺寸不变，应该将缩放因子全部设没为1.0。

高级变换与动画基础

平移，然后旋转

矩阵变换库：cuon-matrix.js

在OpenGL中，我们无须手动指定变换矩阵的每个元素，因为OpenGL提供了一系列有用的函数来帮助我们创建变换矩阵。比如通过调用glTranslate()函数并传入在XY、Z轴上的平移的距离，就可以创建一个平移矩阵(如图4.1所示)。

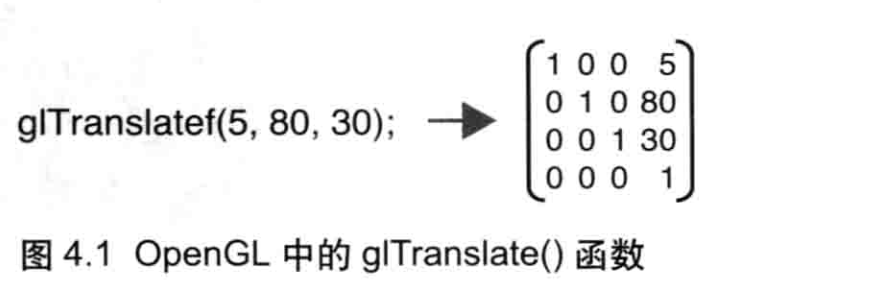
遗憾的是，WebGL 没有提供类似的矩阵函数，如果想要使用它们，你就得自己编写，或者使用其他人已经编写好的。因为矩阵函数非常有用，所以我为本书专门编写了一个JavaScript函数库cuon-matrixjs。该函数库允许你通过与OpenGL中类似的方式创建变换矩阵。虽然这个库是专为本书编写的，你也可以在自己的程序中使用它。

复合变换

下面就来看看如何将两次变换组合起来，即先进行一次平移，再进行一次旋转。

显然，示例中包含了以下两种变换，如图4.3所示:

将三角形沿着X轴平移一段距离。

在此基础上，旋转三角形。

讲解了这么多，我们可以先写下第1条(平移操作)中的坐标方程式。

然后对<平移后的坐标>进行旋转。

当然你也可以分步计算这两个等式，但更好的方法是，将等式41代入到等式42中，把两个等式组合起来:

最后，我们可以在JavaScript中计算<旋转矩阵>x<平移矩阵>，然后将得到的矩阵传人顶点着色器。像这样，我们就可以把多个变换复合起来了。一个模型可能经过了多次变换，将这些变换全部复合成一个等效的变换，就得到了模型变换(modeltransformation)，或称建模变换(modeling transformation)，相应地，模型变换的矩阵称为模型矩阵 (model matrix)。

动画

请求再次被调用（requestAnimationFrame()）

传统习惯上来说，如果你想要JavaScript重复执行某个特定的任务(函数)，你可以使用setInterval()函数。

现代的浏览器都支持多个标签页，每个标签页具有单独的 JavaScript 运行环境，但是自 setInterval() 函数诞生之初,浏览器还没有开始支持多标签页。所以在现代浏览器中，不管标签页是否被激活，其中的 setInterval()函数函数都会反复调用 func，如果标签页比较多，就会增加浏览器的负荷。所以后来,浏览器又引入了requestAnimation()方法,该方法只有当标签页处于激活状态时才会生效。requestAnimationFrame()是新引入的方法，还没有实现标准化。好在Google提供的webgl-utilsjs库提供了该函数的定义并隐藏了浏览器间的差异。

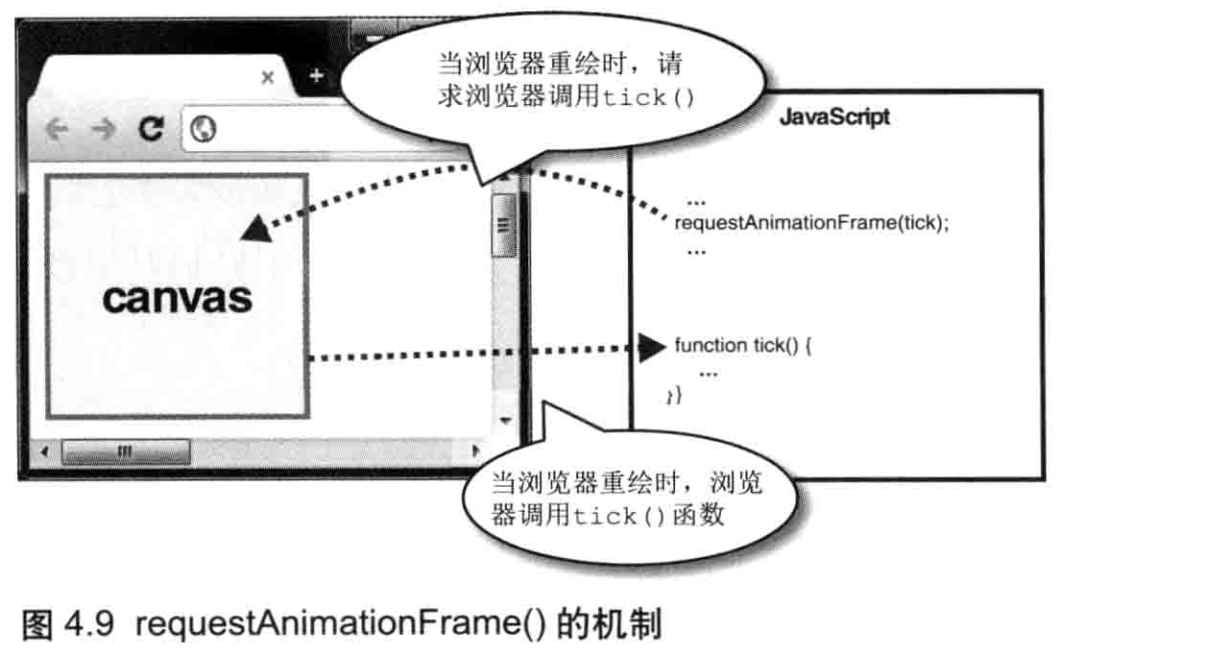
使用这个函数的好处是可以避免在未激活的标签页上运行动画。注意，你无法指定重复调用的间隔;函数 func(第1个参数)会在浏览器需要网页的某个元素(第2个参数)重绘时被调用。此外还需要注意，在浏览器成功(找到了适当的时机)地调用了一次 func 后，想要再次调用它，就必须再次发起请求,因为前一次请求已经结束(也就是说，requestAnimationFrame 更像 setTimeOut 不是 setTimeInterval，不会因为你发起一次请求，就会不停地循环调用 func)。此外，在调用函数后，你需要发出下次调用的请求，因为上一次关于调用的请求在调用完成之后就结束了使命。

如果你想取消请求，需要使用 cancelAnimationFrame()

颜色与纹理

本节将介绍一下内容：

顶点的其他 (非坐标)数据一如颜色等一传人顶点着色器;

发生在顶点着色器和片元着色器之间的从图形到片元的转化，又称为图元光栅化(rasterzation process).

将图像 (或称纹理)映射到图形或三维对象的表面上

将非坐标数据传入顶点着色器

通过创建多个缓冲区对象将多个不同顶点数据传入顶点着色器
示例为传入顶点数据

// MultiAttributeSize.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute float a_PointSize;\n' +
  'void main() {\n' +
  '  gl_Position = a_Position;\n' +
  '  gl_PointSize = a_PointSize;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  'void main() {\n' +
  '  gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex information
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the positions of the vertices');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0.0, 0.0, 0.0, 1.0);

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);

  // Draw three points
  gl.drawArrays(gl.POINTS, 0, n);
}

function initVertexBuffers(gl) {
  var vertices = new Float32Array([
    0.0, 0.5,   -0.5, -0.5,   0.5, -0.5
  ]);
  var n = 3;

  var sizes = new Float32Array([
    10.0, 20.0, 30.0  // Point sizes
  ]);

  // Create a buffer object
  var vertexBuffer = gl.createBuffer();  
  var sizeBuffer = gl.createBuffer();
  if (!vertexBuffer || !sizeBuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // Write vertex coordinates to the buffer object and enable it
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
    if(a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);
  gl.enableVertexAttribArray(a_Position);

  // Bind the point size buffer object to target
  gl.bindBuffer(gl.ARRAY_BUFFER, sizeBuffer);
  gl.bufferData(gl.ARRAY_BUFFER, sizes, gl.STATIC_DRAW);
  var a_PointSize = gl.getAttribLocation(gl.program, 'a_PointSize');
  if(a_PointSize < 0) {
    console.log('Failed to get the storage location of a_PointSize');
    return -1;
  }
  gl.vertexAttribPointer(a_PointSize, 1, gl.FLOAT, false, 0, 0);
  gl.enableVertexAttribArray(a_PointSize);

  // Unbind the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, null);

  return n;
}

gl.vertexAttribPointer() 的步进和偏移参数

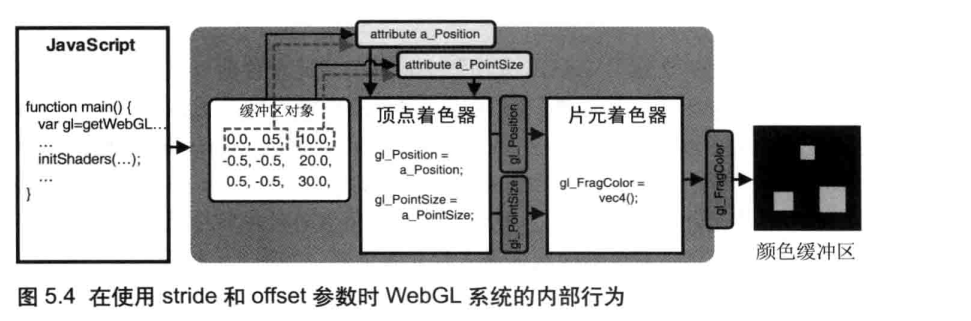
使用多个缓冲区对象向着色器传递多种数据，比较适合数据量不大的情况。当程序中的复杂三维图形具有成千上万个顶点时，维护所有的顶点数据是很困难的。然而，WebGL 允许我们把顶点的坐标和尺寸数据打包到同一个缓冲区对象中，并通过某种机制分别访问缓冲区对象中不同种类的数据。比如，可以将顶点的坐标和尺寸数据按照如下方式交错组织(interleaving)，如例 5.2 所示 :

可见，一旦我们将几种“逐顶点”的数据 (坐标和尺寸)交叉存储在一个数组中,并将数组写人一个缓冲区对象。WebGL就需要有差别地从缓冲区中获取某种特定数据(坐标或尺寸)，即使用gl.vertexAttribPointer()函数的第5个参数stride和第6个参数offset。下面让我们来看看示例程序。

// MultiAttributeSize_Interleaved.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute float a_PointSize;\n' +
  'void main() {\n' +
  '  gl_Position = a_Position;\n' +
  '  gl_PointSize = a_PointSize;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  'void main() {\n' +
  '  gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set vertex coordinates and point sizes
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0.0, 0.0, 0.0, 1.0);

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);

  // Draw three points
  gl.drawArrays(gl.POINTS, 0, n);
}

function initVertexBuffers(gl) {
  var verticesSizes = new Float32Array([
    // 顶点坐标和点的尺寸
     0.0,  0.5,  10.0,  // 第一个点
    -0.5, -0.5,  20.0,  // 第二个点
     0.5, -0.5,  30.0   // 第三个点
  ]);
  var n = 3; // The number of vertices

  // Create a buffer object
  var vertexSizeBuffer = gl.createBuffer();  
  if (!vertexSizeBuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // 绑定缓冲区对象到目标，并写入数据
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexSizeBuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesSizes, gl.STATIC_DRAW);

  // 获取类型化数组中每个元素所占的字节数
  var FSIZE = verticesSizes.BYTES_PER_ELEMENT;
  //Get the storage location of a_Position, assign and enable buffer
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if (a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, FSIZE * 3, 0);
  gl.enableVertexAttribArray(a_Position);  // Enable the assignment of the buffer object

  // Get the storage location of a_PointSize
  var a_PointSize = gl.getAttribLocation(gl.program, 'a_PointSize');
  if(a_PointSize < 0) {
    console.log('Failed to get the storage location of a_PointSize');
    return -1;
  }
  gl.vertexAttribPointer(a_PointSize, 1, gl.FLOAT, false, FSIZE * 3, FSIZE * 2);
  gl.enableVertexAttribArray(a_PointSize);  // Enable buffer allocation

  // Unbind the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, null);

  return n;
}

首先，我们定义了一个类型化数组 verticesSizes 接下来创建缓冲区对象。然后，我们将 verticeSize 数组中每个元素的大小 (字节数)存储到 FSIZE 中，稍后将会用到它。类型化数组具有BYTES_PER_ELEMENT属性，可以从中获知数组中每个元素所占的字节数。

现在，我们就需要着手把缓冲区对象分配给 attribute 变量了。首先获取 attribute变量a_Position 的存储地址，方法和之前完全相同，然后调gl.vertexAttribPointer() 函数。注意,这里的参数设置就与前例有所不同了因为在缓冲区对象中存储了两种类型的数据:顶点坐标和顶点尺寸。

在第3章中曾提到过 gl.vertexAttribpointer() 的函数规范，但是让我们再来看一下其参数sride 和 offset。

参数 stride 表示，在缓冲区对象中，单个顶点的所有数据 (这里，就是顶点的坐标和大小)的字数，也就是相邻两个顶点间的距离，即步进参数。

在前面的示例程序中，缓冲区只含有一种数据，即顶点的坐标，所以将其设置为 0即可。然而，在本例中，当缓冲区中有了多种数据(比如此例中的顶点坐标和顶点尺寸时，我们就需要考虑 stride 的值，如下图所示。

如图 5.3 所示，每一个顶点有3 个数据值 (两个坐标数据和一个尺寸数据)，因此stride 应该设置为每项数据大小的三倍，即 3xESIZE(Eloat32Array 中每个元素所占的字节数)。

参数 ofser 表示当前考虑的数据项距离首个元素的距离，即偏移参数。在verticesSizes 数组中，顶点的坐标数据是放在最前面的，所以 ofser 应当为 0。因此我们调用 gl.vertexAttribArray() 函数时，如下所示传人stride 参数和offset参数。

    gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, FSIZE * 3, 0);
    gl.enableVertexAttribArray(a_Position);

这样一来，我们就把缓冲区中的那部分顶点坐标数据分配给了着色器中的 attribute变量a_Position。

接下来对顶点尺寸数据采取相同的操作:将缓冲区对象中的顶点尺寸数据分配给 apointsize。然而在这个例子中，缓冲区对象还是原来那个，只不过这次关注的数据不同,我们需要将 offset 参数设置为顶点尺寸数据在缓冲区对象中的初始位置。在关于某个顶点的三个值中,前两个是顶点坐标,后一个是顶点尺寸,因此 offset应当设置为 ESIZE*2(参见图 5.3)。我们如下调用 gl.vertexAttribArray() 函数，并正确设置stride 参数和 offset参数。

    gl.vertexAttribPointer(a_PointSize, 1, gl.FLOAT, false, FSIZE * 3, FSIZE * 2);
    gl.enableVertexAttribArray(a_PointSize)

再次执行顶点着色器时，WebGL 系统会根据stride和 ofset 参数，从缓冲区中正确地抽取出数据，依次赋值给着色器中的各个 attribute 变量，并进行绘制 (如图 5.4 所示)。

修改颜色（varying 变量）

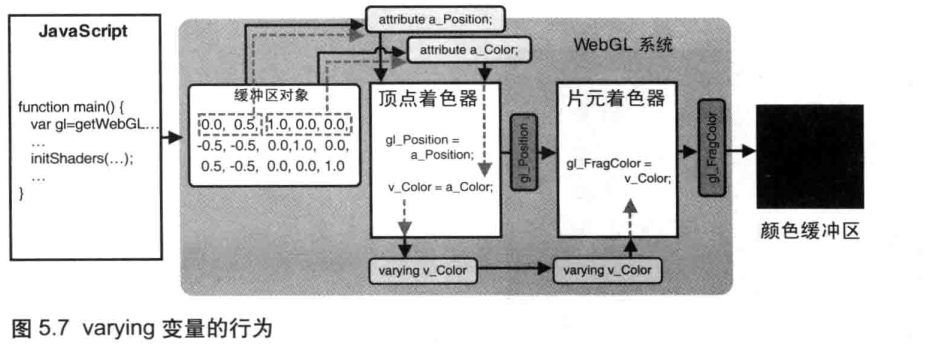
片元着色器可以用来处理颜色之类的属性。但是到目前为止，我们都只是在片元着色器中静态地设置颜色，还没有真正地研究过片元着色器。虽然现在已经能够将顶点的颜色数据从 JavaScript 中传给顶点着色器中的 attribute 变量，但是真正能够影响绘制颜色的 gl_FragColor 却在片元着色器中。我们需要知道顶点着色器和片元着色器是如何交流的，这样才能使传人顶点着色器的数据进入片元着色器，如图 5.6 所示。

我们之前使用了一个uniform变量来将颜色信息传人片元着色器然而，因为这是个“一致的”(uniform)变量，而不是“可变的”(varying)，我们没法为每个顶点都准备一个值，所以那个程序中的所有顶点都只能是同一个颜色。我们使用种新的 varying 变量(varying variable)向片元着色器中传入数据，实际上.varying 变量的作用是从顶点着色器向片元着色器传输数据。

// MultiAttributeColor.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'varying vec4 v_Color;\n' + // varying变量
  'void main() {\n' +
  '  gl_Position = a_Position;\n' +
  '  gl_PointSize = 10.0;\n' +
  '  v_Color = a_Color;\n' +  // 将数据传给片元着色器
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  'precision mediump float;\n' + // Precision qualifier (See Chapter 6)
  'varying vec4 v_Color;\n' +    // 从顶点着色器接收数据
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // 
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0.0, 0.0, 0.0, 1.0);

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);

  // Draw three points
  gl.drawArrays(gl.POINTS, 0, n);
}

function initVertexBuffers(gl) {
  var verticesColors = new Float32Array([
    // Vertex coordinates and color
     0.0,  0.5,  1.0,  0.0,  0.0, 
    -0.5, -0.5,  0.0,  1.0,  0.0, 
     0.5, -0.5,  0.0,  0.0,  1.0, 
  ]);
  var n = 3; // The number of vertices

  // Create a buffer object
  var vertexColorBuffer = gl.createBuffer();  
  if (!vertexColorBuffer) {
    console.log('Failed to create the buffer object');
    return false;
  }

  // Write the vertex coordinates and colors to the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorBuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);

  var FSIZE = verticesColors.BYTES_PER_ELEMENT;
  //Get the storage location of a_Position, assign and enable buffer
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if (a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, FSIZE * 5, 0);
  gl.enableVertexAttribArray(a_Position);  // Enable the assignment of the buffer object

  // Get the storage location of a_Position, assign buffer and enable
  var a_Color = gl.getAttribLocation(gl.program, 'a_Color');
  if(a_Color < 0) {
    console.log('Failed to get the storage location of a_Color');
    return -1;
  }
  gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 5, FSIZE * 2);
  gl.enableVertexAttribArray(a_Color);  // Enable the assignment of the buffer object

  return n;
}

在顶点着色器中，我们声明了 attribute 变量a_color 用以接收颜色数据.然后声明了新的varying变量v_color,该变量负责将颜色值将被传给片元着色器。注意，varying 变量只能是 float (以及相关的vec2，vec3，vec4，mat2，mat3和 mat4)类型的。

我们将 a_color 变量的值直接赋给之前声明的 v_color 变量。

那么，片元着色器该如何接收这个变量呢?答案很简单，只需要在片元着色器中也声明一个 (与顶点着色器中的那个 varying 变量同名) varying 变量就可以了

在 WebGL 中，如果顶点着色器与片元着色器中有类型和命名都相同的 varying 变量,那么顶点着色器赋给该变量的值就会被自动地传入片元着色器.如图 5.7 所示。

彩色三角形（ColoredTriangle.js）

这一节，我们将为三角形的每个顶点指定一个颜色，然后 WebGL 会自动在三角形表面产生颜色平滑过渡的效果。

几何形状的装配和光栅化

以第三章的HelloTriangle的示例（绘制一个红色三角形）为例；

// HelloTriangle.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'void main() {\n' +
  '  gl_Position = a_Position;\n' +
  '}\n'

// Fragment shader program
var FSHADER_SOURCE =
  'void main() {\n' + '  gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' + '}\n'

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl')

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas)
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL')
    return
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.')
    return
  }

  // Write the positions of vertices to a vertex shader
  var n = initVertexBuffers(gl)
  if (n < 0) {
    console.log('Failed to set the positions of the vertices')
    return
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0, 0, 0, 1)

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT)

  // Draw the rectangle
  gl.drawArrays(gl.LINE_LOOP, 0, n)
}

function initVertexBuffers(gl) {
  var vertices = new Float32Array([0, 0.5, -0.5, -0.5, 0.5, -0.5])
  var n = 3 // The number of vertices

  // Create a buffer object
  var vertexBuffer = gl.createBuffer()
  if (!vertexBuffer) {
    console.log('Failed to create the buffer object')
    return -1
  }

  // Bind the buffer object to target
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer)
  // Write date into the buffer object
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW)

  var a_Position = gl.getAttribLocation(gl.program, 'a_Position')
  if (a_Position < 0) {
    console.log('Failed to get the storage location of a_Position')
    return -1
  }
  // Assign the buffer object to a_Position variable
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0)

  // Enable the assignment to a_Position variable
  gl.enableVertexAttribArray(a_Position)

  return n
}

我们在 initvertexBuffers()函数中将顶点坐标写人了缓冲区对象，然后将缓冲区对象分配给a_Position 变量。最后调用 gl.drawArrays()执行顶点着色器。当顶点着色器执行时，缓冲区中的三个顶点坐标依次传给了a_Position 变量，再赋值给 gl_Position，这样 WebGL 系统就可以根据顶点坐标进行绘制。在片元着色器中，我们将红色的 RGBA 值(1.0,0.0,0.0,1.0)赋给gl_EragColor，这样就画出了一个红色的三角形。

可是直到现在，你还是不明白这究竟是如何做到的?在你向 gl_Position 给出了三角形的三个顶点的坐标时，片元着色器又怎样才能进行所谓的逐片元操作呢?

如图 5.9 显示了问题所在，程序向 gl_Position 给出了三个顶点的坐标，谁来确定这三个点就是三角形的三个顶点?最终，为了填充三角形内部，谁来确定哪些像素需要被着色?谁来负责调用片元着色器，片元着色器又是怎样处理每个片元的?

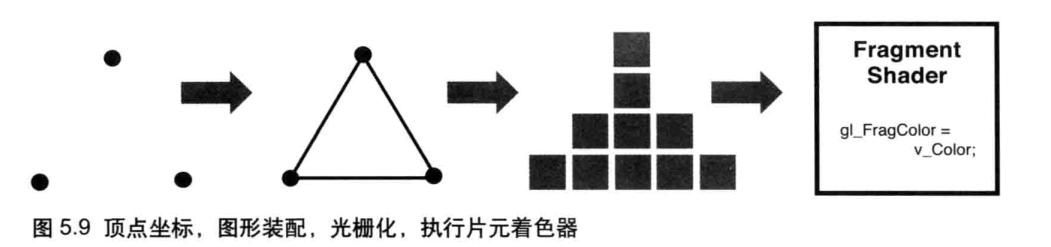
实际上，在顶点着色器和片元着色器之间，有这样两个步骤，如图 5.10 所示。
图形装配过程:这一步的任务是，将孤立的顶点坐标装配成几何图形。几何图形的类别由gl.drawArrays()函数的第一个参数决定。
光栅化过程:这一步的任务是，将装配好的几何图形转化为片元。

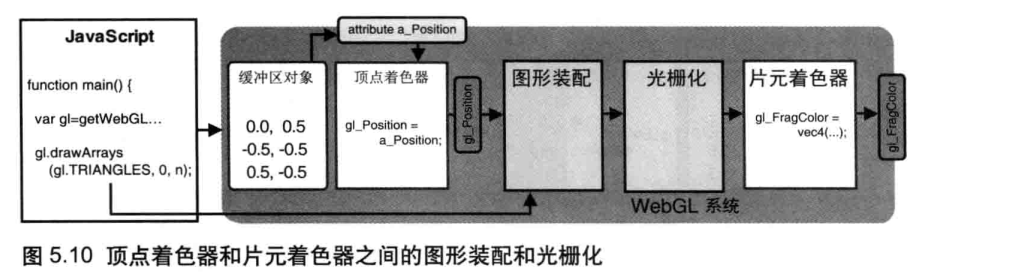
通过图5.10 你就会理解，gl_Position 实际上是几何图形装配(geometric shapeassembly)段的输人数据。注意，几何图形装配过程又被称为图元装配过程(primitiveassembly process)，因为被装配出的基本图形 (点、线、面)又被称为图元(primitives)。

图5.11 显示了在 HelloTriangle.js 中，顶点着色器和片元着色器之间图形装配与光栅化的过程。

在例 5.5 中，gl.drawArrays() 的参数n为3，顶点着色器将被执行 3 次。

第 1步：执行顶点着色器，缓冲区对象中的第 1个坐标(0.0,0.5) 被传递给 attribute变量a_Position。 一旦一个顶点的坐标被赋值给了gl_Position，它就进入了图形装配区域，并暂时储存在那里。你应该还记得，我们仅仅显式地向 a_Position 赋了x分量和y分量,所以向z分量和 w 分量赋的是默认值进入图形装配区域的坐标其实是(0.0,0.5,0.0,1.0)。

第2步：再次执行顶点着色器，类似地，将第 2 个坐标(-0.5,-0.5,0.0,1.0) 传入并储存在装配区。

第3步：第3 次执行顶点着色器，将第3 个坐标(0.5,-0.5,0.0,1.0) 传入并储存在装配区。现在，顶点着色器执行完毕,三个顶点坐标都已经处在装配区了。

第 4步：开始装配图形。使用传人的点坐标,根据 gl.drawArrays() 的第一个参数信息 (gl.TRIANGLES)来决定如何装配。本例使用三个顶点来装配出一个三角形。

第 5步：显示在屏幕上的三角形是由片元 (像素) 组成的，所以还需要将图形转化为片元，这个过程被称为光栅化 (rasterization)。光栅化之后，我们就得到了组成这个三角形的所有片元。在图 5.11 中的最后一步，你可以看到光栅化后得到的组成三角形的片元。

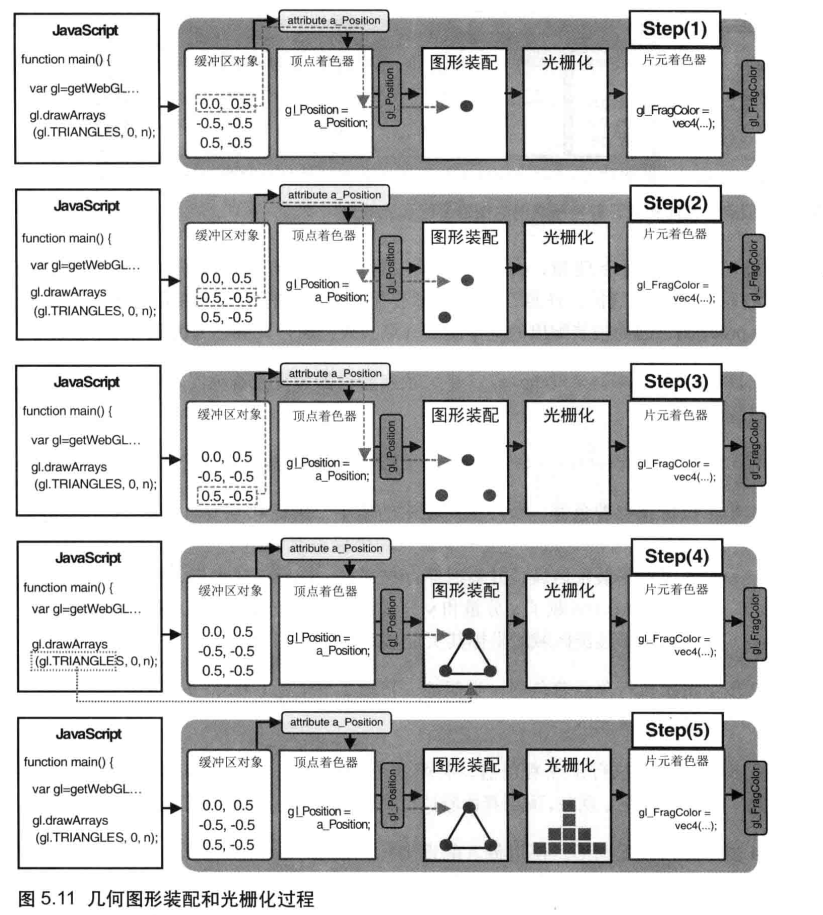
上图为了示意，只显示了10个片元，片元数目就是这个三角形最终在屏幕。实际上上所覆盖的像素数。如果修改了gl.drawArrays()的第 1 个参数，那么第 4 步的图形装配、第 5 步的片元数目和位置就会相应地变化。比如说，如果这个参数是 gI.LINE，程序就会使用前两个点装配出一条线段，舍弃第 3 个点;如果是 gl.LINE LOOP，程序就会将三个点装配成为首尾相接的折线段,并光栅化出一个空心的的三角形(不产生中间的像素)。

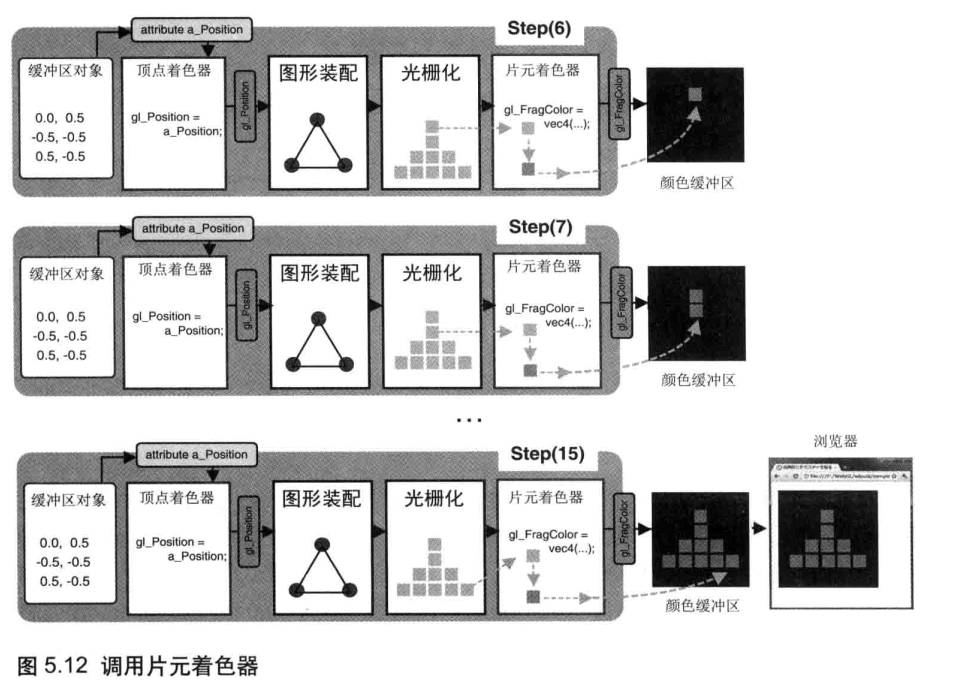
调用片元着色器

一旦光栅化过程结束后，程序就开始逐片元调用片元着色器。在图 5.12 中，片元着色器被调用了 10 次,每调用一次,就处理一个片元 (为了整洁,图5.12 省略了中间步骤)。对于每个片元，片元着色器计算出该片元的颜色，并写入颜色缓冲区。直到第 15 步最后一个片元被处理完成，浏览器就会显示出最终的结果

varying 变量的作用和内插过程

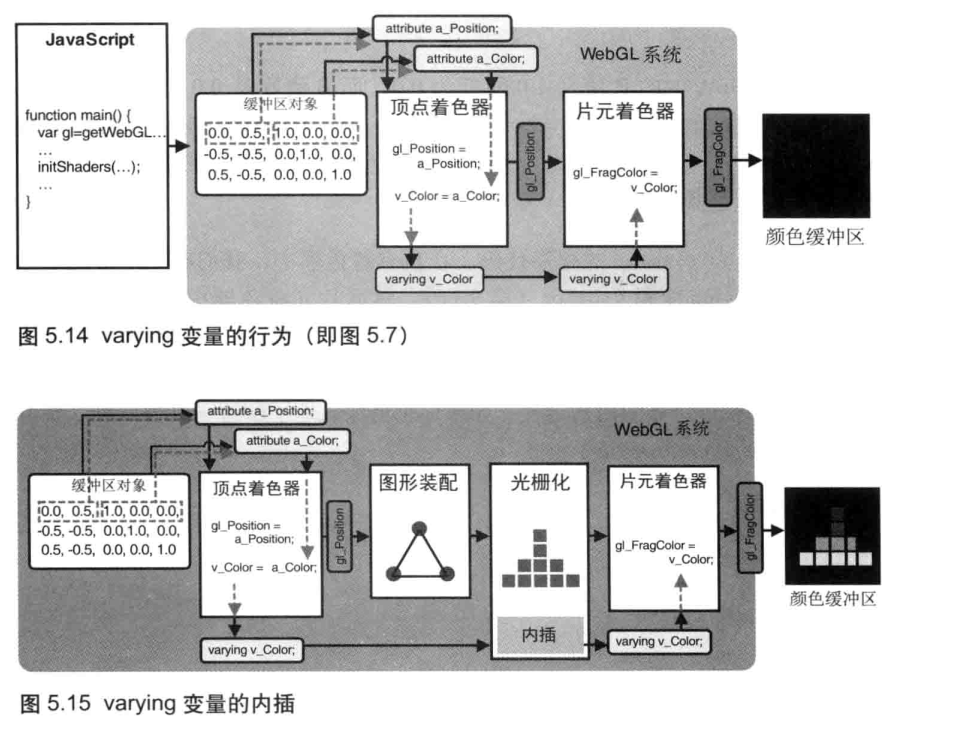
回到图 5.8的 coloredTriangle 程序，这个程序也可以用刚学到的知识来解释为什么在顶点着色器中只是指定了每个顶点的颜色，最后得到了一个具有渐变色彩效果的三角形呢?事实上，我们把顶点的颜色赋值给了顶点着色器中的 varying 变量v_color，它的值被传给片元着色器中的同名、同类型变量 (即片元着色器中的 varying变量v_color),如图 5.14 所示。但是，更准确地说，顶点着色器中的 v_color 变量在传入片元着色器之前经过了内插过程。所以，片元着色器中的v_color 变量和顶点着色器中的v_color 变量实际上并不是一回事,这也正是我们将这种变量称为“varying”(变化的)变量的原因.

更准确地说，在 ColoredTriangle 中，我们在 varying变量中为三角形的3个不同顶点指定了 3 种不同颜色，而三角形表面上这些片元的颜色值都是 WebGL 系统用这3 个顶点的颜色内插出来的。

例如，考虑一条两个端点的颜色不同的线段。一个端点的颜色为红色 (1.0,0.0,0.0),而另一个端点的颜色为蓝色(0.0,0.0,1.0)。我们在顶点着色器中向 varying变量v_color赋上这两个颜色 (红色和蓝色)，那么 WebGL 就会自动地计算出线段上的所有点 (片元)的颜色，并赋值给片元着色器中的 varying 变量v_color (如图 5.16 所示)。

在这个例子中 RGBA 中的R值从 1.0 降低为 0.0，而B值则从 0.0上升至 1.0，线段上的所有片元的颜色值都会被恰当地计算出来一这个过程就被称为内插过程(interpolation process)。一旦两点之间每个片元的新颜色都通过这种方式被计算出来后它们就会被传给片元着色器中的 v_color 变量。

再来看例 5.6 coloredTriangle 的程序代码。在顶点着色器中，我们将三角形的3个顶点的颜色赋给了 varying变量v_color ，然后片元着色器中的 varying变量v_color 就接收到了内插之后的片元颜色。在片元着色器中，我们把片元的颜色赋值给gl_Eragcolor 变量，这样就绘制出了一个彩色的三角形，如图5.8 所示。每个 varying 变量都会经过这样的内插过程。如果你想更深入地了解这一过程，可以参考《计算机图形学》(Computer Graphics)一书。

总之，这一节着重讲述了顶点着色器和片元着色器之间的过程。光栅化是三维图形学的关键技术之一，它负责将矢量的几何图形转变为栅格化的片元 (像素)。图形被转化为片元之后，我们就可以在片元着色器内做更多的事情，如为每个片元指定不同的颜色。颜色可以内插出来，也可以直接编程指定。

在矩形表面贴上图像

在前一节中，我们了解了如何绘制彩色的图形，如何内插出平滑的颜色渐变效果。虽然这种方法很强大，但在更复杂的情况下仍然不够用。比如说，如果你想创建一张逼真的砖墙，问题就来了。你可能会试图创建很多个三角形，指定它们的颜色和位置来模拟墙面上的坑坑洼洼。如果你真这么做了，那就陷人了繁琐和无意义的苦海中。

你可能已经知道，在三维图形学中，有一项很重要的技术可以解决这个问题，那就是纹理映射(texture mapping)。纹理映射其实非常简单，就是将一张图像 (就像一张贴纸)映射 (贴) 到一个几何图形的表面上去。将一张真实世界的图片贴到一个由两个三角形组成的矩形上，这样矩形表面看上去就是这张图片。此时，这张图片又可以称为纹理图像(texture image)或纹理(texture)。

纹理映射的作用，就是根据纹理图像，为之前光栅化后的每个片元涂上合适的颜色。组成纹理图像的像素又被称为纹素(texels，texture elements)，每一个纹素的颜色都使用RGB 或 RGBA 格式编码，如图 5.18 所示。

在 WebGL 中，要进行纹理映射，需遵循以下四步:

准备好映射到几何图形上的纹理图像。

为几何图形配置纹理映射方式。

加载纹理图像，对其进行一些配置，以在WebGL中使用它。

在片元着色器中将相应的纹素从纹理中抽取出来，并将纹素的颜色赋给片元。

纹理坐标

第 2 步指定映射方式，就是确定“几何图形的某个片元”的颜色如何取决于“纹理图像中哪个 (或哪几个)像素”的问题(即前者到后者的映射)。我们利用图形的顶点坐标来确定屏幕上哪部分被纹理图像覆盖，使用纹理坐标(texture coordinates)来确定纹理图像的哪部分将覆盖到几何图形上。纹理坐标是一套新的坐标系统。

纹理坐标是纹理图像上的坐标，通过纹理坐标可以在纹理图像上获取纹素颜色。WebGL 系统中的纹理坐标系统是二维的，如图 5.20 所示。为了将纹理坐标和广泛使用的x坐标和y坐标区分开来，WebGL 使用 s 和t命名纹理坐标 (st 坐标系统)

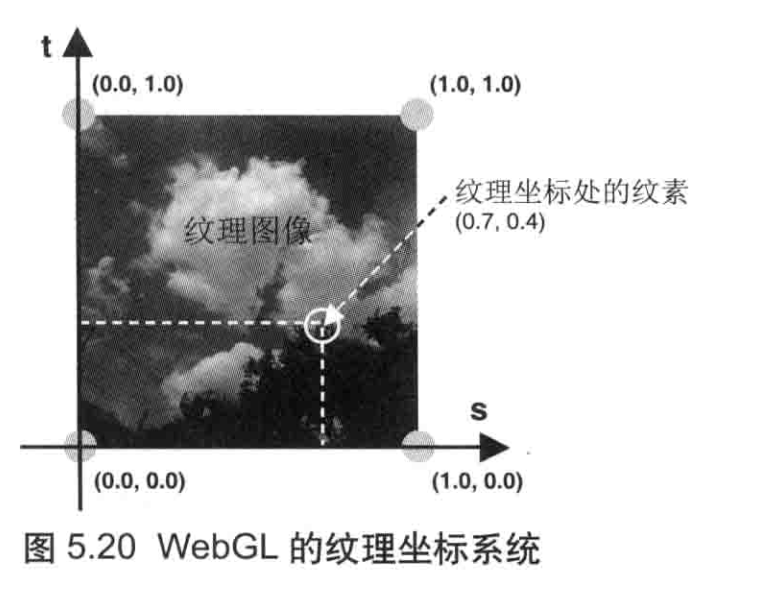
如图 5.20 所示，纹理图像四个角的坐标为左下角 (0.0,0.0)，右下角(1.0,0.0)，右上角(1.0,1.0) 和左上角(0.0,1.0)。纹理坐标很通用，因为坐标值与图像自身的尺寸无关不管是 128x 128 还是 128x256 的图像，其右上角的纹理坐标始终是(1.0,1.0)。

将纹理图像粘贴到几何图形上

如前所述，在 WebGL 中，我们通过纹理图像的纹理坐标与几何形体顶点坐标间的映射关系，来确定怎样将纹理图像贴上去，如图 5.21 所示。

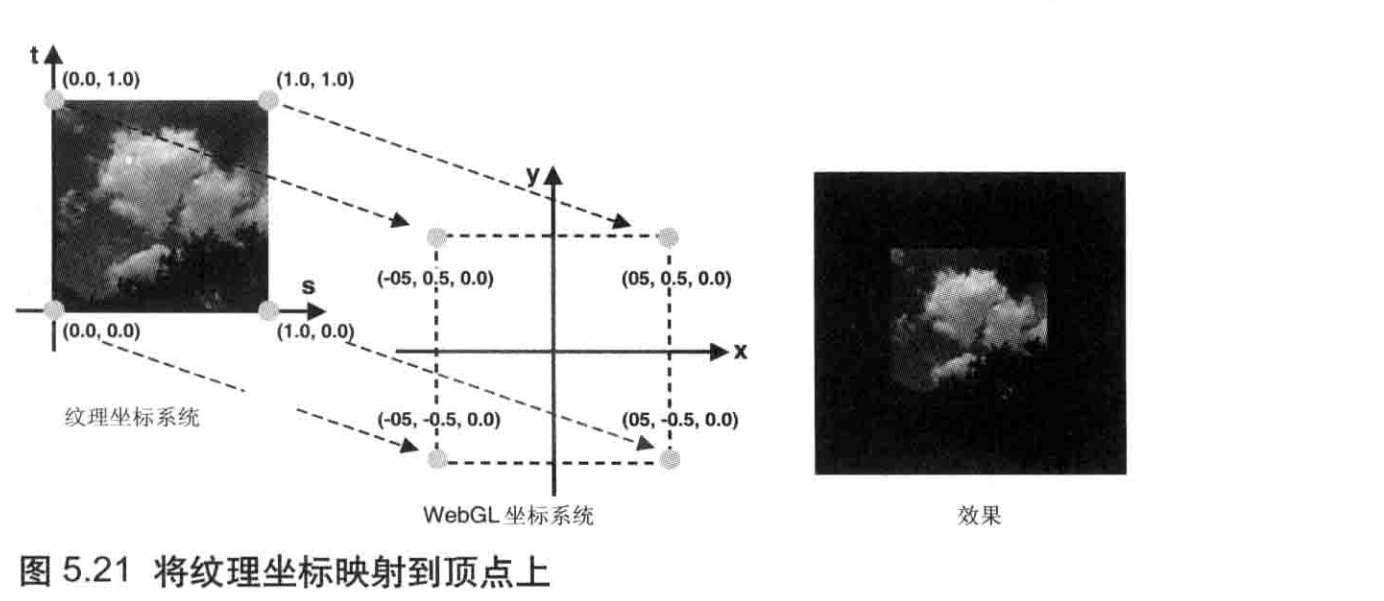
在这里，我们将纹理坐标(0.0,1.0) 映射到顶点坐标(-0.5,-0.5,0.0) 上，将纹理坐标(1.0,1.0) 映射到顶点坐标 (0.5,0.5,0.0) 上，等等。通过建立矩形四个顶点与纹理坐标的对应关系，就获得了如图 5.21 (右)所示的结果

// TexturedQuad.js (c) 2012 matsuda and kanda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec2 a_TexCoord;\n' +
  'varying vec2 v_TexCoord;\n' +
  'void main() {\n' +
  '  gl_Position = a_Position;\n' +
  '  v_TexCoord = a_TexCoord;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'uniform sampler2D u_Sampler;\n' +
  'varying vec2 v_TexCoord;\n' +
  'void main() {\n' +
  '  gl_FragColor = texture2D(u_Sampler, v_TexCoord);\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // 设置顶点信息
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0.0, 0.0, 0.0, 1.0);

  // 配置纹理
  if (!initTextures(gl, n)) {
    console.log('Failed to intialize the texture.');
    return;
  }
}

function initVertexBuffers(gl) {
  var verticesTexCoords = new Float32Array([
    // 顶点坐标， 纹理坐标
    -0.5,  0.5,   0.0, 1.0,
    -0.5, -0.5,   0.0, 0.0,
     0.5,  0.5,   1.0, 1.0,
     0.5, -0.5,   1.0, 0.0,
  ]);
  var n = 4; // The number of vertices

  // Create the buffer object
  var vertexTexCoordBuffer = gl.createBuffer();
  if (!vertexTexCoordBuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // 将顶点坐标和纹理坐标写入缓冲区对象
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexTexCoordBuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesTexCoords, gl.STATIC_DRAW);

  var FSIZE = verticesTexCoords.BYTES_PER_ELEMENT;
  //Get the storage location of a_Position, assign and enable buffer
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if (a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, FSIZE * 4, 0);
  gl.enableVertexAttribArray(a_Position);  // Enable the assignment of the buffer object

  // Get the storage location of a_TexCoord
  var a_TexCoord = gl.getAttribLocation(gl.program, 'a_TexCoord');
  if (a_TexCoord < 0) {
    console.log('Failed to get the storage location of a_TexCoord');
    return -1;
  }
  // Assign the buffer object to a_TexCoord variable
  gl.vertexAttribPointer(a_TexCoord, 2, gl.FLOAT, false, FSIZE * 4, FSIZE * 2);
  gl.enableVertexAttribArray(a_TexCoord);  // Enable the assignment of the buffer object

  return n;
}

function initTextures(gl, n) {
  var texture = gl.createTexture();   // 创建纹理对象
  if (!texture) {
    console.log('Failed to create the texture object');
    return false;
  }

  // 获取 u_Sampler的存储位置
  var u_Sampler = gl.getUniformLocation(gl.program, 'u_Sampler');
  if (!u_Sampler) {
    console.log('Failed to get the storage location of u_Sampler');
    return false;
  }
  var image = new Image();  // 创建一个image对象
  if (!image) {
    console.log('Failed to create the image object');
    return false;
  }
  // 注册图像加载事件的响应函数
  image.onload = function(){ loadTexture(gl, n, texture, u_Sampler, image); };
  // 浏览器开始加载图像
  image.src = '../resources/sky.jpg';

  return true;
}

function loadTexture(gl, n, texture, u_Sampler, image) {
  gl.pixelStorei(gl.UNPACK_FLIP_Y_WEBGL, 1); // 对纹理图像进行y轴反转
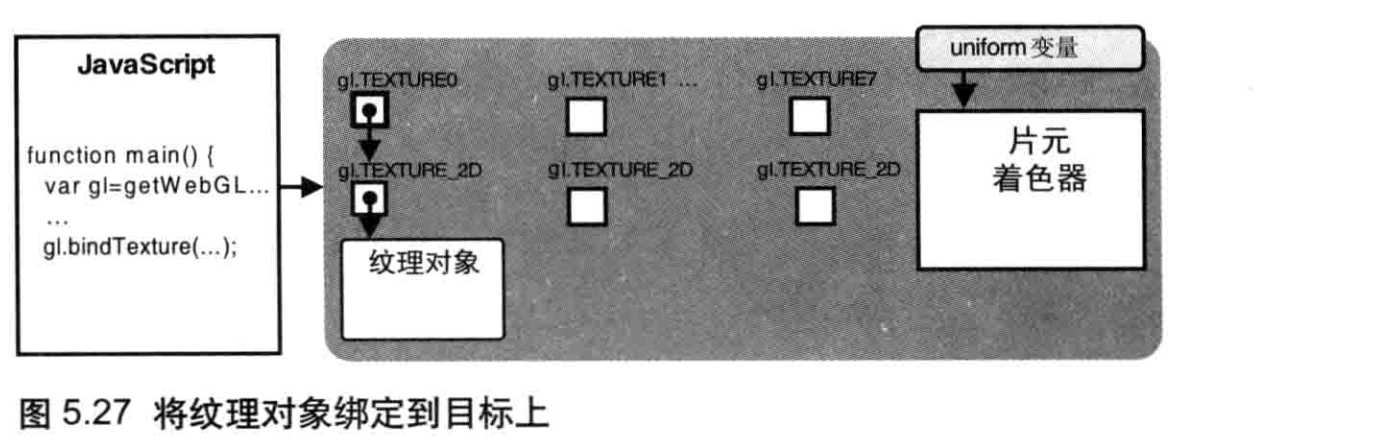
  // 开启0号纹理单元
  gl.activeTexture(gl.TEXTURE0);
  // 向target绑定纹理对象
  gl.bindTexture(gl.TEXTURE_2D, texture);

  // 配置纹理参数
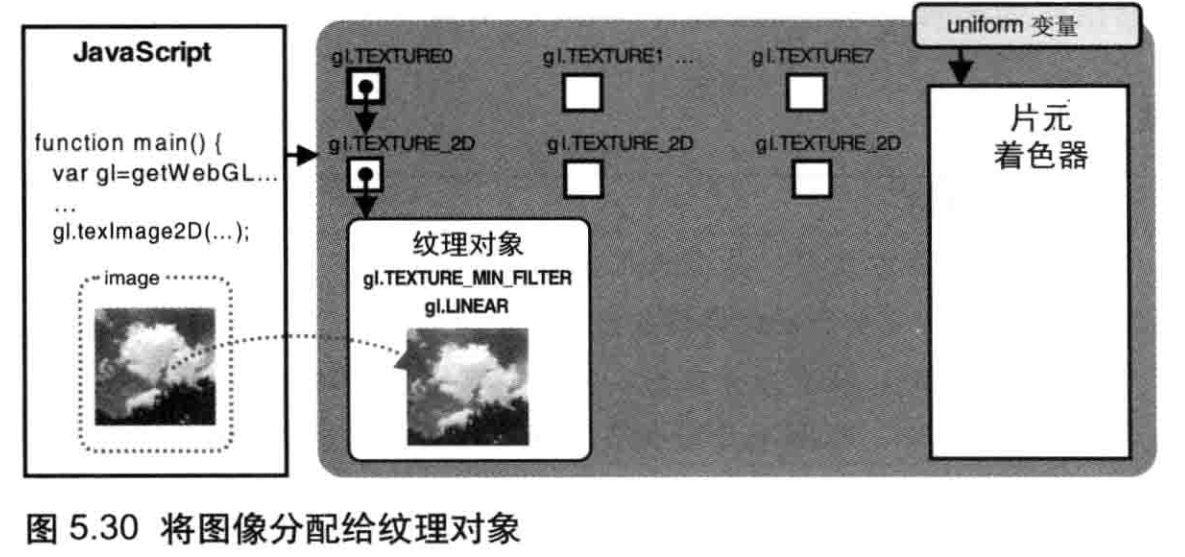
  gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_MIN_FILTER, gl.LINEAR);
  // 配置纹理图像
  gl.texImage2D(gl.TEXTURE_2D, 0, gl.RGB, gl.RGB, gl.UNSIGNED_BYTE, image);
  
  // 将0号纹理传递给着色器
  gl.uniform1i(u_Sampler, 0);
  
  gl.clear(gl.COLOR_BUFFER_BIT);   // Clear <canvas>

  gl.drawArrays(gl.TRIANGLE_STRIP, 0, n); // 绘制矩形
}

纹理映射的过程需要顶点着色器和片元着色器二者的配合:首先在顶点着色器中为每个顶点指定纹理坐标，然后在片元着色器中根据每个片元的纹理坐标从纹理图像中抽取纹素颜色。程序主要包括五个部分，已经在代码中用数字标记了出来。

这段程序主要分五个部分。

顶点着色器中接收顶点的纹理坐标，光栅化后传递给片元着色器。

片元着色器根据片元的纹理坐标，从纹理图像中抽取出纹素颜色，赋给当前片元。

设置顶点的纹理坐标( initVertexBuffers() )。

准备待加载的纹理图像，令浏览器读取它( initTextures() )。

监听纹理图像的加载事件，某天加载完成，就在WebGL系统中使用纹理( loadtexture() )。

设置纹理坐标（initVertexBuffers()）

将纹理坐标和顶点坐标写在同一个缓冲区中;定义数组verticesTexCoords，成对记录每个顶点的顶点坐标和纹理坐标。

  var verticesTexCoords = new Float32Array([
    // 顶点坐标和纹理坐标
    -0.5,  0.5,   0.0, 1.0,
    -0.5, -0.5,   0.0, 0.0,
     0.5,  0.5,   1.0, 1.0,
     0.5, -0.5,   1.0, 0.0,
  ]);

可见，第1个顶点(-050.5)对应的纹理坐标是(001.0)，第2个顶点(-0.5,-0.5)对应的纹理坐标是(000.0)，第3个顶点(0.50.5)对应的纹理坐标是(1.01.0)，第4个顶点(0.5-0.5)对应的纹理坐标是(1000)。图5.21显示了这种对应关系。

然后我们将顶点坐标和纹理坐标写入缓冲区对象，将其中的顶点坐标分配给a_Position变量并开启。接着，获取a_TexCoord变量的存储位置。将缓冲区中的纹理坐标分配给该变量，并开启。

配置和加载纹理（ initTextures() ）

initTextures() 函数负责配置和加载纹理：首先调用gl.createTexture()创建纹理对象，纹理对象用来管理 WebGL 系统中的纹理。然后调用gl.getUniformLocation()从片元着色器中获取uniform变量u_Sampler(取样器)存储位置，该变量用来接收纹理图像。

gl.createTexture()方法可以创建纹理对象。

调用该函数将在WebGL系统中创建一个纹理对象，如图5.22所示。gl.TEXTURE0 到gl.TEXTURE7是管理纹理图像的8个纹理单元(稍后将详细解释)，每一个都与gl.TEXTURE_2D相关联，而后者就是绑定纹理时的纹理目标。稍后将会详细解释这些内容。

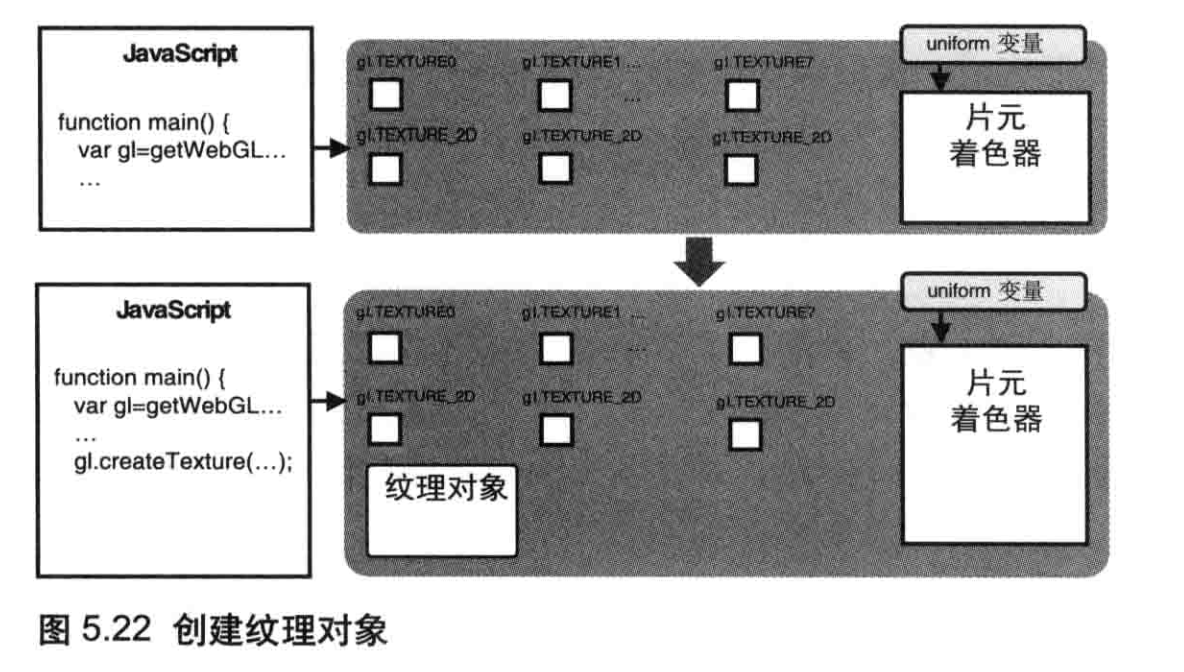
同样，也可以使用gl.deleteTexture()来删除一个纹理对象。注意，如果试图删除一个已经被删除的纹理对象，不会报错也不会产生任何影响。

接下来，请求浏览器加载纹理图像供WebGL使用，该纹理图像将会映射到矩形上。

为WebGL 配置纹理（ loadTexture() ）

该函数的主要任务是配置纹理供WebGL使用。使用纹理对象的方式与使用缓冲区很类似，下面就让我们研究一下。

图像Y 轴反转

在使用图像之前，你必须对它进行Y轴反转。

gl.pixelStorei(gl.UNPACK_FLIP_Y_WEBGL, 1); 	// 对纹理图像进行Y轴反转

该方法对图像进行了Y轴反转。如图 5.24 所示，WebGL 纹理坐标系统中的t轴的方向和 PNG、BMP、JPG 等格式图片的坐标系统的Y轴方向是相反的。因此，只有先将图像Y轴进行反转，才能够正确地将图像映射到图形上。(或者，你也可以在着色器中手动反转t轴坐标。)

下面是gl.pixelstorei()方法的规范:

激活纹理单元（gl.activeTexture()）

WebGL通过一种称作纹理单元(textureunit)的机制来同时使用多个纹理。每个纹理单元有一个单元编号来管理一张纹理图像。
即使你的程序只需要使用一张纹理图像，也得为其指定一个纹理单元。

系统支持的纹理单元个数取决于硬件和浏览器的 WebGL 实现，但是在默认情况下，WebGL 至少支持8个纹理单元，一些其他的系统支持的个数更多。内置的变量g1.TEXTRUE0、g1TEXTURE1……g1TEXTURE7各表示一个纹理单元。

在使用纹理单元之前，还需要调用gl.activeTexture()来激活它，如图5.26所示。

gl.activeTexture(gl.TEXTURE0); // 开启0号纹理单元

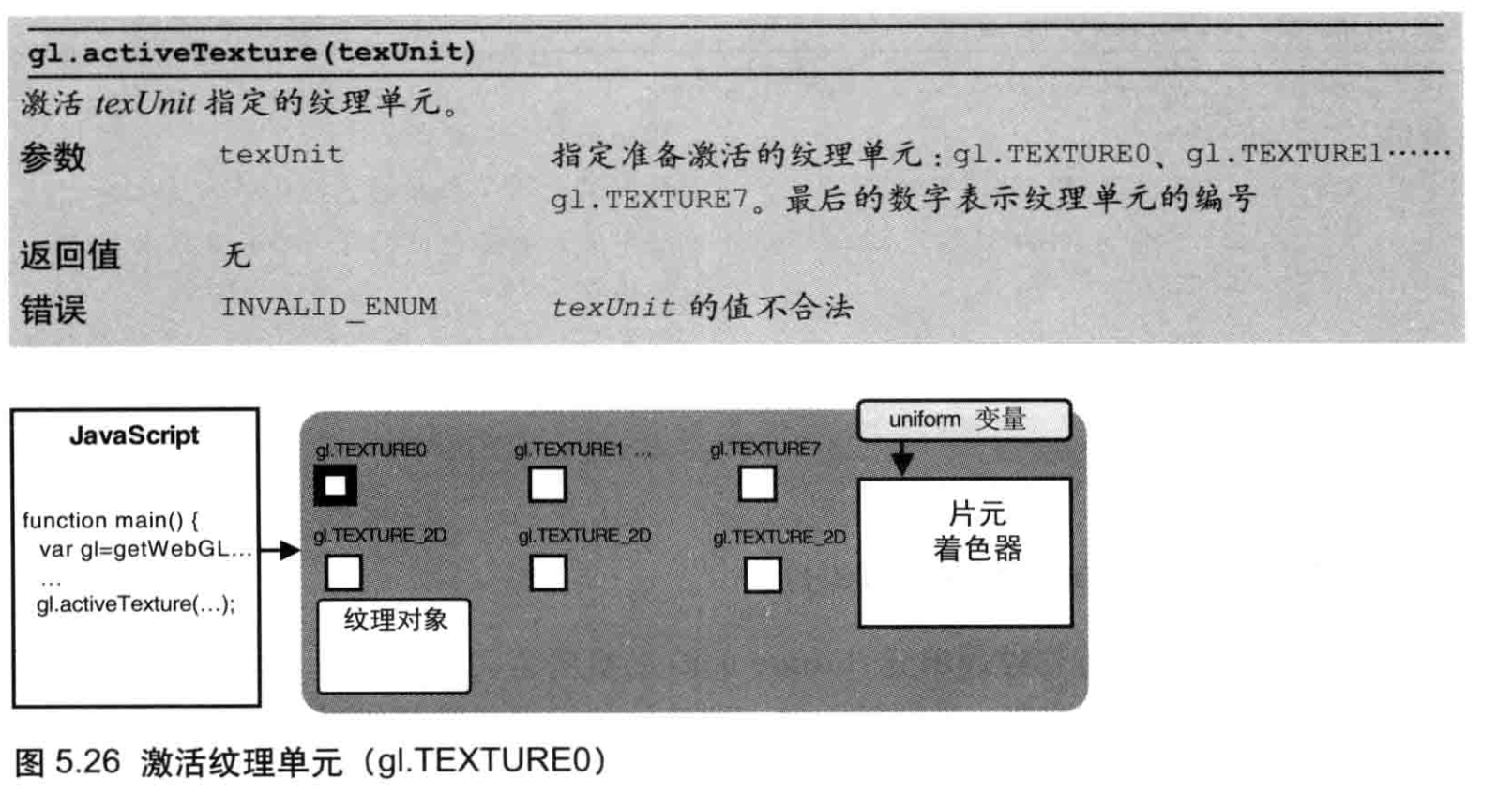
绑定纹理对象（gl.bindTexture()）

接下来，你还需要告诉 WebGL 系统纹理对象使用的是哪种类型的纹理。在对纹理对象进行操作之前，我们需要绑定纹理对象，这一点与缓冲区很像：在对缓冲区对象进行操作(如写入数据)之前，也需要绑定缓冲区对象。WebGL支持两种类型的纹理，如表5.2所示。

注意，该方法完成了两个任务：开启纹理对象，以及将纹理对象绑定到纹理单元上。在本例中，因为0号纹理单元(g1.TEXTURE0)已经被激活了，所以在执行完gl.texImage2D方法后，WebGL系统的内部状态就如图5.27所示。

这样，我们就指定了纹理对象的类型(gl.TEXTURE_2D)。本书将始终使用该类型的纹理。实际上，在 WebGL 中，你没法直接操作纹理对象，必须通过将纹理对象绑定到纹理单元上，然后通过操作纹理单元来操作纹理对象。

配置纹理对象的参数（gl.texParameteri()）

接下来，还需要配置纹理对象的参数，以此来设置纹理图像映射到图形上的具体方式：如何根据纹理坐标获取纹素颜色、按哪种方式重复填充纹理。我们使用通用函数gl.texParameteri来设置这些参数。

如图5.28所示，通过pname可以指定4个纹理参数。

放大方法(gl.TEXTURE_MAG_FILTER)：这个参数表示，当纹理的绘制范围比纹理本身更大时，如何获取纹素颜色。比如说，你将16x16的纹理图像映射到32x32像素的空间里时，纹理的尺寸就变成了原始的两倍。WebGL 需要填充由于放大而造成的像素间的空隙，该参数就表示填充这些空隙的具体方法。

缩小方法(gl.TEXTURE_MIN_FILTER)：这个参数表示，当纹理的绘制范围比纹理本身更小时，如何获取纹素颜色。比如说，你将32x32的纹理图像映射到16x16像素的空间里，纹理的尺寸就只有原始的一半。为了将纹理缩小，WebGL 需要剔除纹理图像中的部分像素，该参数就表示具体的剔除像素的方法。

水平填充方法(g1.TEXTURE_WRAP_S):这个参数表示，如何对纹理图像左侧或右侧的区域进行填充。

垂直填充方法(gl.TEXTURE_WRAP_T):这个参数表示，如何对纹理图像上方和下方的区域进行填充。

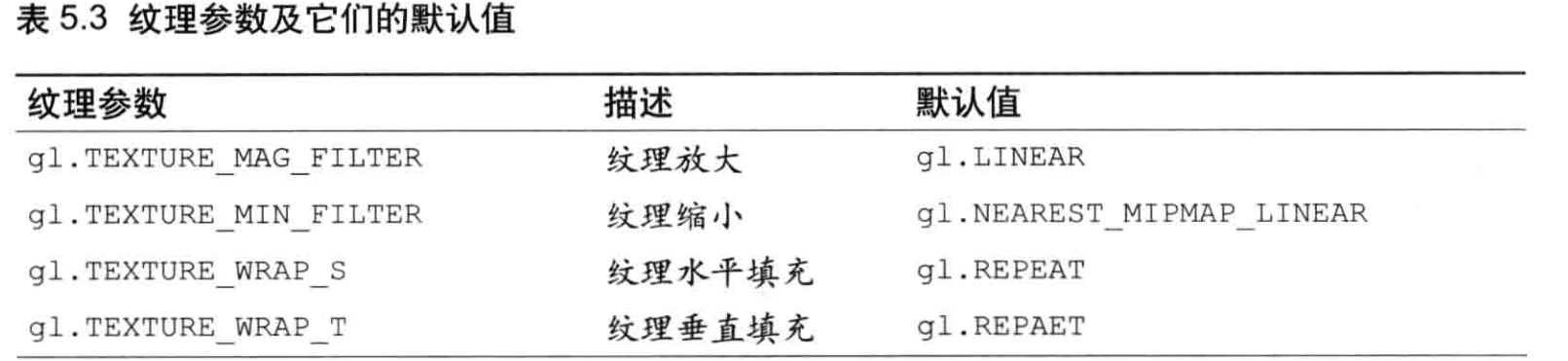
表5.4显示了可以赋给g1TEXTURE MAG FILTER和g1TEXTURE MIN FILTER的常量;
表5.5显示了可以赋给g1TEXTURE WRAP S和g1TEXTURE WRAP T的常量。

如表5.3所示，每个纹理参数都有一个默认值，通常你可以不调用gl.texParameteri()就使用默认值。然而，本例修改了gl.TEXTURE_MIN_FILTER参数，它的默认值是一种特殊的、被称为MIPMAP(也称金字塔)的纹理类型。MIPMAP纹理实际上是一系列纹理，或者说是原始纹理图像的一系列不同分辨率的版本。本书中不大会用到这种类型，也不作详细介绍了。总之，我们把参数gl.TEXTURE_MIN_FILTER设置为gl.LINEAR。

  gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_MIN_FILTER, gl.LINEAR);

纹理对象的参数都被设置好后，WebGL系统的内部状态如图5.29所示。

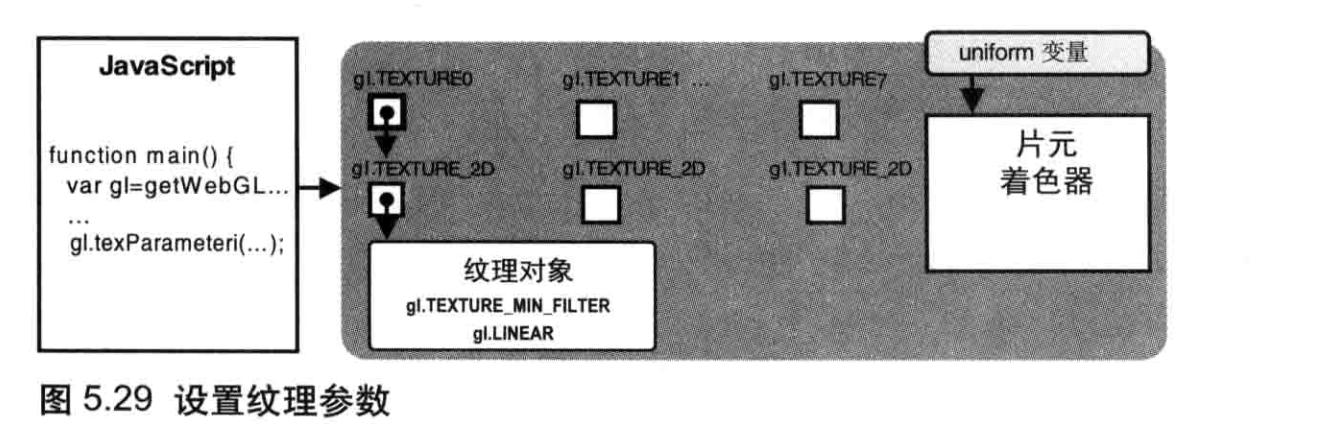
接下来，我们将纹理图像分配给纹理对象。

将纹理图像分配给纹理对象（ gl.texImage2D() ）

我们使用gl.texImage2D()方法将纹理图像分配给纹理对象，同时该函数还允许你告诉WebGL系统关于该图像的一些特性。

 gl.texImage2D(gl.TEXTURE_2D, 0, gl.RGB, gl.RGB, gl.UNSIGNED_BYTE, image);

这时，Image对象中的图像就从JavaScript传入WebGL系统中，并存储在纹理对象中，如图5.30所示。

快速看一下调用该方法时每个参数的取值。level参数直接用0就好了，因为我们没用到金字塔纹理。format参数表示纹理数据的格式，具体取值如表5.6所示，你必须根据纹理图像的格式来选择这个参数。示例程序中使用的纹理图片是 JPG格式的，该格
式将每个像素用 RGB三个分量来表示，所以我们将参数指定为g1.RGB。对其他格式的图像，如 PNG 格式的图像，通常使用 g1.RGBA，BMP 格式的图像通常使用 g1.RGB而g1.LUMINANCE 和 g1.LUMINANCE_ALPHA 通常用在灰度图像上等等,

这里的流明 (luminance)表示我们感知到的物体表面的亮度。通常使用物体表面红、绿、蓝颜色分量值的加权平均来计算流明。

如图5.30所示，g1.texImage2D()方法将纹理图像存储在了WebGL系统中的纹理对象中。一日存储，你必须通过internalformat参数告诉系统纹理图像的格式类型。在WebGL中，internalformat必须和format一样。

type参数指定了纹理数据类型，见表5.7。通常我们使用gl.UNSIGNED_BYTE数据类型当然也可以使用其他数据类型，如gl.UNSIGNED_SHORT_5_6_5(将RGB三分量压缩人16比特中)。后面的几种数据格式通常被用来压缩数据，以减少浏览器加载图像的时间。

将纹理单元传递给片元着色器（ gl.uniform1i() ）

一旦将纹理图象传入了WebGL系统，就必须将其传人片元着色器并映射到图形的表面上去。如前所述，我们使用uniform变量来表示纹理，因为纹理图像不会随着片元变化。

  'uniform sampler2D u_Sampler;\n' +
  'varying vec2 v_TexCoord;\n' +
  'void main() {\n' +
  '  gl_FragColor = texture2D(u_Sampler, v_TexCoord);\n' +
  '}\n';

必须将着色器中表示纹理对象的 uniform 变量声明为一种特殊的、专用于纹理对象的数据类型，如表5.8所示。示例程序使用二维纹理gl.TEXTURE_2D，所以该uniform变量的数据类型设为sampler2D。

在initTextures()函数中，我们获取了uniform变量u_Sampler的存储地址，并将其作为参数传给loadTexture()函数。我们必须通过指定纹理单元编号(texture unitnumber)(即gl,TEXTUREn中的n)将纹理对象传给u_Sampler。本例唯一的纹理对象被绑定在了g1.TEXTUREO上，所以调用gluniformi()时，第2个参数为0。

  // 将0号纹理传递给着色器中的取样器变量
  gl.uniform1i(u_Sampler, 0);

在执行完该代码后，WebGL系统的内部状态如图5.31所示，这样片元着色器就终于能够访问纹理图像了。

从顶点着色器向片元着色器传输纹理坐标

由于我们是通过attribute变量a_TexCoord接收顶点的纹理坐标，所以将数据赋值给varying变量v_TexCoord并将纹理坐标传入片元着色器是可行的。你应该还记得，片元着色器和顶点着色器内的同名、同类型的varying变量可用来在两者之间传输数据。顶点之间片元的纹理坐标会在光栅化的过程中内插出来，所以在片元着色器中，我们使用的是内插后的纹理坐标。

// 顶点着色器
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec2 a_TexCoord;\n' +
  'varying vec2 v_TexCoord;\n' +
  'void main() {\n' +
  '  gl_Position = a_Position;\n' +
  '  v_TexCoord = a_TexCoord;\n' +
  '}\n';

这样就完成了在WebGL系统中使用纹理的所有准备工作。

剩下的工作就是，根据片元的纹理坐标，从纹理图像上抽取出纹素的颜色，然后涂到当前的片元上。

在片元着色器中获取纹理像素颜色（ texture2D() ）

片元着色器从纹理图像上获取纹素的颜色。

gl_FragColor = texture2D(u_Sampler, v_TexCoord)

使用 GLSL ES 内置函数 texture2D() 来抽取纹素颜色。该函数很容易使用，只需要传人两个参数--纹理单元编号和纹理坐标，就可以取得纹理上的像素颜色。这个函数是内置的，留意一下其参数类型和返回值。

纹理放大和缩小方法的参数将决定 WebGL 系统将以何种方式内插出片元。我们将texture2D()函数的返回值赋给了glFragColor变量，然后片元着色器就将当前片元染成这个颜色。最后，纹理图像就被映射到了图形(本例中是一个矩形)上，并最终被画了出来。

这已经是进行纹理映射的最后一步了。此时，纹理已经加载好、设置好，并映射到了图形上，就等你画出来了。

如你所见，在WebGL中进行纹理映射是一个相对复杂的过程，一方面是因为你得让浏览器去加载纹理图像;另一方面是因为，即使只有一个纹理，你也得使用纹理单元。但是，一日你掌握了这些基本的步骤，以后使用起来就会得心应手多了。

使用多幅纹理

WebGL可以同时处理多幅纹理，纹理单元就是为了这个目的而设计的。之前的示例程序都只用到了一幅纹理，也只用到了一个纹理单元。这一节的示例程序MultiTexture来在矩形上重叠粘贴两幅纹理图像。通过本例，你可以进一步了解纹理单元的机制。图5.34显示了MultiTexture的运行效果，两张纹理图像在矩形上的混合效果如下。

图5.35中的两幅图分别显示了示例程序用到的两幅纹理图像。为了说明WebGL具有处理不同纹理图像格式的能力，本例故意使用了两种不同格式的图像。

最关键的是，你需要对每一幅纹理分别进行前一节所述的将纹理图像映射到图形表面的操作，以此来将多张纹理图像同时贴到图形上去。

// MultiTexture.js (c) 2012 matsuda and kanda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec2 a_TexCoord;\n' +
  'varying vec2 v_TexCoord;\n' +
  'void main() {\n' +
  '  gl_Position = a_Position;\n' +
  '  v_TexCoord = a_TexCoord;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'uniform sampler2D u_Sampler0;\n' +
  'uniform sampler2D u_Sampler1;\n' +
  'varying vec2 v_TexCoord;\n' +
  'void main() {\n' +
  '  vec4 color0 = texture2D(u_Sampler0, v_TexCoord);\n' +
  '  vec4 color1 = texture2D(u_Sampler1, v_TexCoord);\n' +
  '  gl_FragColor = color0 * color1;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex information
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0.0, 0.0, 0.0, 1.0);

  // Set texture
  if (!initTextures(gl, n)) {
    console.log('Failed to intialize the texture.');
    return;
  }
}

function initVertexBuffers(gl) {
  var verticesTexCoords = new Float32Array([
    // Vertex coordinate, Texture coordinate
    -0.5,  0.5,   0.0, 1.0,
    -0.5, -0.5,   0.0, 0.0,
     0.5,  0.5,   1.0, 1.0,
     0.5, -0.5,   1.0, 0.0,
  ]);
  var n = 4; // The number of vertices

  // Create a buffer object
  var vertexTexCoordBuffer = gl.createBuffer();
  if (!vertexTexCoordBuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // Write the positions of vertices to a vertex shader
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexTexCoordBuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesTexCoords, gl.STATIC_DRAW);

  var FSIZE = verticesTexCoords.BYTES_PER_ELEMENT;
  //Get the storage location of a_Position, assign and enable buffer
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if (a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, FSIZE * 4, 0);
  gl.enableVertexAttribArray(a_Position);  // Enable the assignment of the buffer object

  // Get the storage location of a_TexCoord
  var a_TexCoord = gl.getAttribLocation(gl.program, 'a_TexCoord');
  if (a_TexCoord < 0) {
    console.log('Failed to get the storage location of a_TexCoord');
    return -1;
  }
  gl.vertexAttribPointer(a_TexCoord, 2, gl.FLOAT, false, FSIZE * 4, FSIZE * 2);
  gl.enableVertexAttribArray(a_TexCoord);  // Enable the buffer assignment

  return n;
}

function initTextures(gl, n) {
  // Create a texture object
  var texture0 = gl.createTexture(); 
  var texture1 = gl.createTexture();
  if (!texture0 || !texture1) {
    console.log('Failed to create the texture object');
    return false;
  }

  // Get the storage location of u_Sampler0 and u_Sampler1
  var u_Sampler0 = gl.getUniformLocation(gl.program, 'u_Sampler0');
  var u_Sampler1 = gl.getUniformLocation(gl.program, 'u_Sampler1');
  if (!u_Sampler0 || !u_Sampler1) {
    console.log('Failed to get the storage location of u_Sampler');
    return false;
  }

  // Create the image object
  var image0 = new Image();
  var image1 = new Image();
  if (!image0 || !image1) {
    console.log('Failed to create the image object');
    return false;
  }
  // Register the event handler to be called when image loading is completed
  image0.onload = function(){ loadTexture(gl, n, texture0, u_Sampler0, image0, 0); };
  image1.onload = function(){ loadTexture(gl, n, texture1, u_Sampler1, image1, 1); };
  // Tell the browser to load an Image
  image0.src = '../resources/sky.jpg';
  image1.src = '../resources/circle.gif';

  return true;
}
// Specify whether the texture unit is ready to use
var g_texUnit0 = false, g_texUnit1 = false; 
function loadTexture(gl, n, texture, u_Sampler, image, texUnit) {
  gl.pixelStorei(gl.UNPACK_FLIP_Y_WEBGL, 1);// Flip the image's y-axis
  // Make the texture unit active
  if (texUnit == 0) {
    gl.activeTexture(gl.TEXTURE0);
    g_texUnit0 = true;
  } else {
    gl.activeTexture(gl.TEXTURE1);
    g_texUnit1 = true;
  }
  // Bind the texture object to the target
  gl.bindTexture(gl.TEXTURE_2D, texture);   

  // Set texture parameters
  gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_MIN_FILTER, gl.LINEAR);
  // Set the image to texture
  gl.texImage2D(gl.TEXTURE_2D, 0, gl.RGBA, gl.RGBA, gl.UNSIGNED_BYTE, image);
  
  gl.uniform1i(u_Sampler, texUnit);   // Pass the texure unit to u_Sampler
  
  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);

  if (g_texUnit0 && g_texUnit1) {
    gl.drawArrays(gl.TRIANGLE_STRIP, 0, n);   // Draw the rectangle
  }
}

首先，让我们来看一下片元着色器。在TextureQuadjs中片元着色器只用到了一个纹理，所以也就只准备了一个uniform变量u_Sampler。然而，本例中的片元着色器用到了两个纹理，那就需要定义两个uniform变量，如下所示:

然后，在片元着色器的main()函数中，我们从两个纹理中取出纹素颜色，分别存储在变量color0和color1中。

使用两个纹素来计算最终的片元颜色(gl_FragColor)有多种可能的方法。示例程序使用的是颜色矢量的分量乘法--两个矢量中对应的分量相乘作为新矢量的分量，如图5.36所示。这很好理解。在GLSLES中，只需要将两个vec4变量简单相乘一下就可以达到目的。

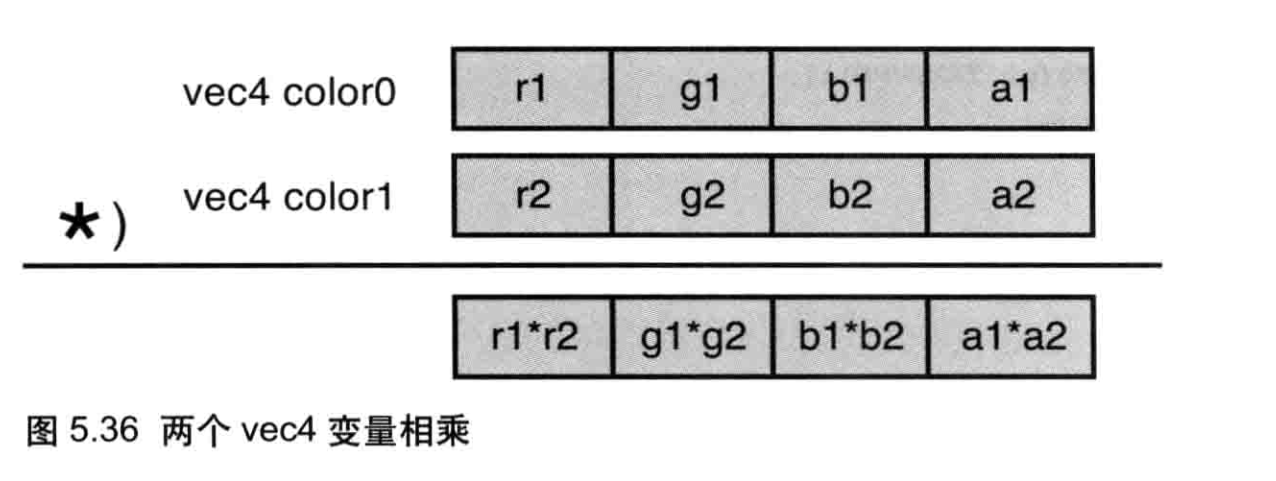
虽然示例程序用到了两个纹理图像，但是initVertexBuffers()函数却没有改变，因为矩形顶点在两幅纹理图像上的纹理坐标是完全相同的。

创建了两个纹理对象，变量名的后缀(texture0中的“0”和texturel中的“1”)对应着纹理单元的编号(纹理单元1或纹理单元0)。此外uniform变量与Image对象也采用了类似的命名方式。

注册事件响应函数loadTexture()的过程与TexturedQuadjs类似，注意最后一个参数是纹理单元编号。

需要注意的是，在本例的loadTexture()函数中，我们无法预测哪一幅纹理图像先被加载完成，因为加载的过程是异步进行的。只有当两幅纹理图像都完成加载时，程序才会开始绘图。为此，我们定义了两个全局变量g_texUnit0和g_texUnit1来指示对应的纹理是否加载完成。

这些变量都被初始化为false。当任意一幅纹理加载完成时，就触发onload事件并调用响应函数loadTexture()。该函数首先根据纹理单元编号0或1来将g_texUnit0或g_texUnit1赋值为true。换句话说，如果触发本次onload事件的纹理的编号是0，那么0号纹理单元就被激活了，并将g_texUnit0设置为true;如果是1，那么1号纹理单元被激活了，并将g_texUnit0设置为ture。

接着，纹理单元编号texUnit被赋给了uniform变量。注意texUnit是通过gluniformli()方法传入着色器的。在两幅纹理图像都完成加载后，WebGL系统内部的状态就如图5.37所示。

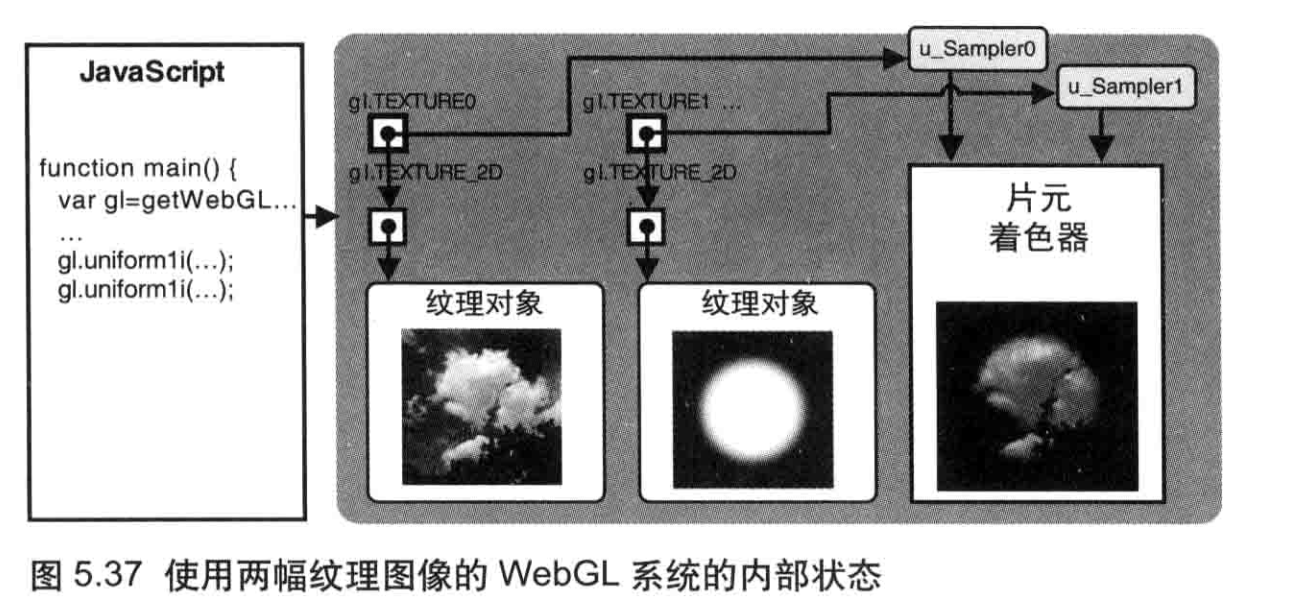
loadTexture()数的最后通过检查g_texUnit0和g_texUnit1变量来判断两幅冬像是否全部完成加载了。如果是，就开始执行顶点着色器，在图形上重叠着绘制出两层纹理，如图 5.34所示。

OpenGL ES 着色器语言（GLSL ES）

GLSL ES 概述

GLSL ES 编程语言是在 OpenGL 着色器语言(GLSL)的基础上，删除和简化一部分功能后形成的。GLSL ES 的目标平台是消费电子产品或嵌入式设备，如智能手机或游戏主机等，因此简化 GLSL ES 能够允许硬件厂商对这些设备的硬件进行简化，由此带来的好处是降低了硬件的功耗，以及更重要的，减少了性能开销。

GLSL ES 的语法与 C 语言的较为类似 (虽然也存在不小的差异)。所以，如果你熟悉 C 语言，就会发现 GLSL ES 很容易理解。此外，着色器语言也开始被用来完成一些通用的任务，如图像处理和数据运算 (即所谓的 GPGPU)，这意味着 GLSL ES 有着广泛的应用前景，花点时间来学习它是完全值得的。

基础

就像很多其他语言一样，使用 GLSL ES 编写着色器程序时，应该注意以下两点 :

程序是大小写敏感的 (marina 和 Marina 不同)。

每一个语句都应该以一个英文分号 (;)结束。

执行顺序

对 JavaScript 而言，一旦脚本加载完成，就从第1行逐行执行 (解释)了。但是着色器程序和 C语言更接近，它从 main() 函数开始执行的。着色器程序必须有且仅有个 main() 函数，而且该函数不能接收任何参数。

main 函数前的 void 关键字表示这个函数不返回任何值。在 JavaScript 中,不管一个函数会不会有返回值,你都是直接用 function 关键字来定义它。而在 GLSL ES 中，如果一个函数有返回值，就必须在定义函数时明确地指定返回值的类型，如果函数没有返回值，也需要用 void 来明确表示这个函数没有返回值。

注释

在着色器程序中，你可以添加注释，而且注释的格式和 JavaScript 中的注释格式是相同的。所以，GLSL ES 支持以下两种形式的注释。

单行注释:// 后直到换行处的所有字符为注释

多行注释:/和/之间的所有字符为注释

数据值类型（数值和布尔值）

GLSL 支持两种数据值类型：

数值类型：GLSL ES支持整型数（如1，2，3）和浮点数（如：3.14，29.98）。没有小数点（.）的值被认为是整型数，而有小数点的值则被认为是浮点数。

布尔值类型：GLSL ES支持布尔值类型，包括true和false两个布尔常量。

GLSL ES不支持字符串类型，虽然字符串对三维图形语言来说还是有一定意思。

变量

你可以使用任何变量名，只要该变量名符合 :

只包括 a-z，A-Z，0-9 和下划线 (_)

变量名的首字母不能是数字。

不能是表 6.1 中所列出的关键字，也不能是表 6.2 中所列出的保留字。但是，你的变量名的一部分可以是它们。比如,变量名 if 是不合法的,但是变量名 iffy 却可以使用

不能以 gl_、webgl_或_webgl_开头，这些前缀已经被 OpenGL ES 保留了

GLSL ES 是强类型语言

GLSL ES 不像 JavaScript，使用 var 关键字来声明所有变量。GLSL ES 要求你具体地指明变量的数据类型。我们在示例程序中用了这种方式声明变量:

<类型><变量名>

我们知道，在定义如 main() 函数这类函数的时候，必须指定函数的返回值。同样在进行赋值操作 (=) 的时候，等号左右两侧的数据类型也必须一样,否则就会出错。

因此，GLSL ES 被称为强类型语言(type sensitive language)，你必须时刻注意变量的类型。

基本类型

GLSL ES支持的基本类型如表6.3所示：

为变量指定类型有利于 WebGL 系统检查代码错误，提高程序的运行效率。下面是些声明基本类型变量的例子 :

float klimt; // 变量是一个浮点数
int utrillo; // 变量是一个整型数
bool doga; // 变量是一个布尔值

赋值和类型转换

使用等号 (=)可以将值赋给变量。我们说过，GLSL ES 是强类型语言，所以如果等号左侧变量的类型与等号右侧的值 (或变量)类型不一致，就会出错。

要将一个整型数值赋值给浮点型变量，需要将整型数转换成浮点数，这个过程称为类型转换。比如，我们可以使用内置的函数 float() 来将整型数转换为浮点数，如下所示:

int i = 8;
float f1 = float(i); // 将8转换为8.0并赋值给f1
float f2 = float(8); // 同上

GLSL ES 支持以下几种用于类型转换的内置函数，如表 6.4 所示 :

运算符

GLSL ES 支持的运算类型与 JavaScript 类似，如表 6.5 所示。

矢量和矩阵

GLSL ES 支持矢量和矩阵类型这两种数据类型很适合用来处理计算机图形。矢量和矩阵类型的变量都包含多个元素，每个元素是一个数值 (整型数、浮点数或布尔值)。矢量将这些元素排成一列，可以用来表示顶点坐标或颜色值等，而矩阵则将元素划分成行和列，可以用来表示变换矩阵。图 6.1 给出了矢量和矩阵的例子

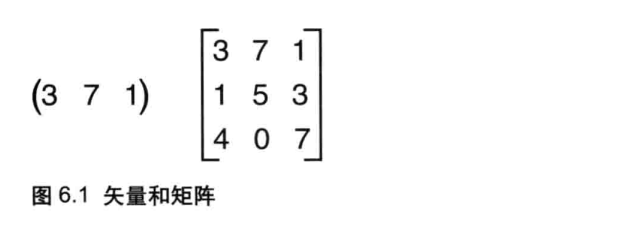
GLSL ES 支持多种不同的矢量和矩阵类型，如表 6.6 所示。

vec3 position //	由三个浮点数元素组成的矢量
							//	比如：(10.0,20.0,30.0)

ivec2 offset	//	由两个整型数元素组成的矢量
							//	比如: (10,20)
							
mat4 mvpMartrix	//	4x4矩阵，每个元素为一个浮点数

赋值和构造

我们使用等号 (=)来对矢量和矩阵进行赋值操作。记住，赋值运算符左右两边的变量/值的类型必须一致，左右两边的(矢量或矩阵的)元素个数也必须相同。比如下面的代码就会出错。

vec4 position = 1.0	//	vec4变量需要4个浮点分量

这里，vec4 类型变量有 4 个元素，你应当以某种方式传人 4 个浮点数值。通常我们使用与数据类型同名的内置构造函数来生成变量，对于 vec4 类型来说，就可以使用内置的 vec4() 函数。比如，如果要创建4个分量各是 1.0、2.0.3.0和 4.0的 vec4 类型变量，你就可以像下面这样调用 vec4() 函数。

vec4 position = vec4(1.0,2.0,3.0,4.0)

这种专门创建指定类型的变量的函数被称为构造函数(constructor functions)，构造函数的名称和其创建的变量的类型名称总是一致的。

矢量构造函数

在 GLSL ES 中，矢量非常重要，所以 GLSL ES 提供了丰富灵活的方式来创建矢量比如 :

vec3 v3 = vec3(1.0,0.0,0.5)	//	将v3设为(1.0, 0.0, 0.5)
vec2 v2 = vec2(v3)	//	使用v3的前两个元素，将v2设为(1.0, 0.0)
vec4 v4 = vec4(1.0)	//	将v4设置为(1.0, 1.0, 1.0, 1.0)

在第 2 行代码中，构造函数忽略了 v3 的第 3 个分量，只用其第 1 个和第 2 个分量创建了一个新的变量。类似地，在第3行代码中，只向构造函数中传人了一个参数 1.0，构造函数就会自动地将这个参数值赋给新建矢量的所有元素。但是，如果构造函数接收了不止 1 个参数，但是参数的个数又比矢量的元素个数少，那么就会出错。

最后，也可以将多个矢量组合成一个矢量，比如 :

vec4 v4b = vec4(v2, v4)	//	将v4b设为(1.0, 0.0, 1.0, 1.0)

这里的规则是，先把第 1个参数v2 的所有元素填充进来，如果还未填满，就继续用第 2 个参数 v4 中的元素填充

矩阵构造函数

矩阵构造函数的使用方式与矢量构造函数的使用方式很类似。但是，你要保证存储在矩阵中的元素是按照列主序排列的（细节请参见图 3.27“列主序”)。下面几个例子显示了使用矩阵构造函数的不同方式。

向矩阵构造函数中传人矩阵的每一个元素的数值来构造矩阵，注意传人值的顺序必须是列主序的。

向矩阵构造函数中传入一个或多个矢量，按照列主序使用矢量里的元素值来构造矩阵。

向矩阵构造函数中传入矢量和数值，按照列主序使用矢量里的元素值和直接传入的数值来构造矩阵。

向矩阵构造函数中传入单个数值，这样将生成一个对角线上元素都是该数值，他元素为 0.0 的矩阵。

与矢量构造函数类似，如果传入的数值的数量大于 1，又没有达到矩阵元素的数量就会出错。

mat m4 = mat4(1.0, 2.0, 3.0) // 错误: mat4对象需要16个元素

访问元素

为了访问矢量或矩阵中的元素，可以使用 · 或 [ ] 运算符。

运算符

在矢量变量名后接点运算符 (.)，然后接上分量名就可以访问矢量的元素了。矢量的分量名如表 6.7 所示。

由于矢量可以用来存储顶点的坐标，颜色和纹理坐标，所以GLSL ES 支持以上三种分量名称以增强程序的可读性。事实上任何矢量的 x、r或 s 分量都会返回第 1 个分量，y、g、t分量都返回第 2 个分量等等。如果你愿意，你可以随意地交换使用它们。比如:

vec3 v3 = vec3(1.0，2.0，3.0);	// 将v3设为(1.0，2.0，3.0)float f;
f = v3.x;	// 设f为1.0
f = v3.y;	// 设f为2.0
f = v3.z;	// 设f为3.0
f=v3.r; 	// 设f为1.0
f = v3.s;	// 设f为1.0

将 (同一个集合的)多个分量名共同置于点运算符后，就可以从矢量中同时抽取出多个分量。这个过程称作混合 (swizzling)。在下面这个例子中，我们使用了 x、y、z和 w,其他的集合也有相同的效果

vec2 v2;
v2 = v3.xy;	// 设v2为(1.0，2.0)
v2 = v3.yz;	// 设v2为(2.0，3.0) 可以省略任意分量
v2 = v3.xz; // 设v2为(1.0，3.0) 可以跳过任意分量
v2 = v3.yx;	// 设v2为(2.0，1.0) 可以逆序
v2 = v3.xx;	// 设v2为(1.0，1.0) 可以重复任意分量
vec3 v3a;
v3a = v3.zyx;	// 设v3a为(3.0，2.0，1.0)，可以使用所有分量

聚合分量名也可以用来作为赋值表达式 (=)的左值

vec4 position = vec4 (1.0，2.0，3.0，4.0);
position.xw = vec2(5.0,6.0);	// position = (5.0，2.0，3.0,6.0)

记住，此时的多个分量名必须属于同一个集合，比如说，你不能使用 v3.was。

[ ]运算符

除了 · 运算符，还可以使用 [ ] 运算符并通过数组下标来访问矢量或矩阵的元素。矩阵中的元素仍然是按照列主序读取的。与在 JavaScript 中一样，下标从0开始.意，所以通过 [0] 可以访问到矩阵中的第1列元素，[1] 可以访问到第2 列元素，[2] 可以访问到第 3 列元素，等等

此外，连续使用两个 [ ] 运算符可以访问某列的某个元素

同样，你也可以同时使用 [] 运算符和分量名来访问矩阵中的元素

运算符

表 6.8 显示了矢量和矩阵所支持的运算。矩阵和矢量的运算符与基本类型(比如整数)的运算符很类似。注意对于矢量和矩阵，只可以使用比较运算符中的 == 和!=，不可以使用 >、<、>= 和 <=。如果你想比较矢量和矩阵的大小，应该使用内置函数. lessThan。

注意，当运算赋值操作作用与矢量或矩阵时，实际上是逐分量地对矩阵或矢量的每一个元素进行独立的运算赋值。

示例

下面这些例子显示了矢量和矩阵在运算时的常见情形。我们假设，在这些例子中变量是如下定义的 :

vec3 v3a，v3b，v3c;
mat3 m3a, m3b, m3c;
float f;

矢量和浮点数的运算

矢量运算

矩阵和浮点数的运算

矩阵右乘矢量

矩阵左乘矢量

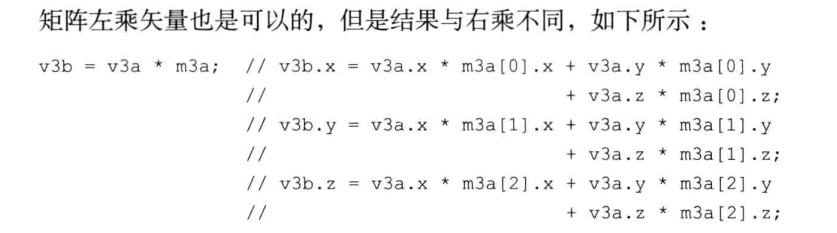
矩阵和矩阵想乘

结构体

GLSL ES 支持用户自定义的类型，即结构体(structures)。使用关键字 struct，将已存在的类型聚合到一起，就可以定义为结构体。比如 :

struct light {	// 定义了结构体类型light
vec4 color;
vec3 position;
}
light 11,12;	// 声明了light类型的变量l1和l2

上面这段代码定义了一种新的结构体类型 light，它包含两个成员:color 变量和position 变量。在定义结构体之后，我们又声明了两个 light 类型的变量 11和12。和 C语言不同的是，没有必要使用 typedef 关键字来定义结构体，因为结构体的名称会自动成为类型名。

此外，为了方便，可以在同一条语句中定义结构体并声明该结构体类型的变量，如下所示 :

struct light {	// 定义结构体和定义变量同时进行
vec4 color;	// 光的颜色
vec3 position;	// 广元位置
} l1;	//该结构体类型的变量l1

赋值和构造

结构体有标准的构造函数，其名称与结构体名一致。沟造函数的参数的顺序必须与结构体定义中的成员顺序一致。图 6.2 显示了结构体构造函数的使用方法。

访问成员

在结构体变量名后跟点运算符 (.)，然后再加上成员名，就可以访问变量的成员。比如 :

vec4 color = 11.color;
vec3 position = 11.position;

运算符

结构体的成员可以参与其自身类型支持的任何运算.但是结构体本身只支持两种运算:赋值 (=) 比较 ( == 和 != )如表 6.9 所示。

当且仅当两个结构体变量所对应的所有成员都相等时，== 运算符才会返回 true，如果任意某个成员不相等，那么!= 运算符返回 true。

数组

GLSLES 支持数组类型。与JavaScript中的数组不同的是，GLSL ES 只支持一维数组，而且数组对象不支持 pop0) 和 push() 等操作，创建数组时也不需要使用 new 运算符。声明数组很简单，只需要在变量名后加上中括号 ()和数组的长度。比如 :

float floatArray[4];	// 声明含有4个浮点数元素的数组
vec4 vec4Array[2];	// 声明含有2个vec4对象的数组

数组的长度必须是大于0的整型常量表达式 (intergral constant expression)，如下定义 :

整型字面量(如0或 1)。

用 const 限定字修饰的全局变量或局部变量(参阅“const 变量”一节)，不包括函数参数。

由前述两条中的项组成的表达式

数组元素可以通过索引值来访问，和 C 语言一样，索引值也是从 0开始的。

只有整型常量表达式和 uniform 变量(见“uniform 变量”一节)可以被用作数组的索引值。此外，与JavaScript 或 C 不同，数组不能在声明时被一次性地初始化，而必须显式地对每个元素进行初始化。如下所示 :

vec4Array[0] = vec4(4.0，3.0，6.0，1.0);
vec4Array[1] = vec4 (3.0，2.0，0.0，1.0);

数组本身只支持 [ ] 运算符，但数组的元素能够参与其自身类型支持的任意运算。比floatArray 利 vec4Array 的元素可以参与下面这此运算如，

// 将floatArray的第2个元素乘以3.14
float f = floatArray[1] *3.14;
// 将vec4Array的第1个元素乘以vec4(1.0，2.0，3.0，4.0);
vec4 v4 = vec4Array[0] * vec4(1.0，2.0，3.0，4.0);

取样器（纹理）

将 GLSL ES 支持的一种内置类型称为取样器(sampler)，我们必须通过该类型变量访问纹理(参见第 5 章“使用颜色和纹理”)。有两种基本的取样器类型 :sampler2D 和samplerCube。取样器变量只能是 uniform 变量(参见“uniform 变量”一节)，或者需要访问纹理的函数，如 texture2D() 函数的参数 (参见附录 B)。比如 :

uniform sampler2D u_Sampler;

此外，唯一能赋值给取样器变量的就是纹理单元编号，而且你必须使用 WebGL 方法 gl.uniformli() 来进行赋值。比如在第 5 章的 TexturedQuad.js 中，我们就使用了gl.uniformli(u Sampler，0) 将纹理单元编号0传给着色器。

除了 =、== 和!=，取样器变量不可以作为操作数参与运算。

和前几节中介绍的其他类型不同，取样器类型变量受到着色器支持的纹理单元的最大数量限制，见表 6.10。该表格中，mediump 是一个精度限定字。(将在本章最后的“精度限定字”一节详细讨论。)

运算符优先级

运算符优先级顺序如表 6.11 所示，注意表中有几个运算符本书将不会解释，这里将其列出来仅供参考。

程序流程控制：分支和循环

着色器中的分支与循环与 JavaScript 或 C 中的几乎无异。

if 语句和if-else 语句

可以使用 if 语句或 if-else 语句进行分支判断，以控制程序流程。

if 语句或 if-else 语句中都必须包含一个布尔值，或者是产生布尔值的表达式。此处不可以使用布尔值类型矢量，比如 bvec2。

GLSL ES 中没有 switch 语句，你也应该注意，过多的 if 或 if-else 语句会降低着色器的执行速度。

for 语句

for 语句的格式如下所示 :
for (初始化表达式  ; 条件表达式  ;循环步进表达式  ) {
	反复执行这里。
}

for(ini i = 0; i < 3 ; i++){
  sum += 1;
}

注意，循环变量 (即例中的 i)只能在初始化表达式中定义，条件表达式可以为空,如果这样做，空的条件表达式返回 true。此外，for 语句还有这样一些限制。

只允许有一个循环变量，循环变量只能是 int 或 float 类型。

循环表达式必须是以下的形式 (假设 i 是循环变量)
i+=,i++,i-- 常量表达式或 i-= 常量表达式 ;

条件表达式必须是循环变量与整型常量的比较 (参见“数组”一节)。

在循环体内，循环变量不可被赋值

这些限制的存在是为了使编译器就能够对 for 循环进行内联展开。

continue、break 和discard 语句

就像在 JavaScript 和 C 语言中一样.通常，我们只能在 for 语句中使用 continue 和 break。通常我们将它们与 if 语句搭配使用。

continue 中止包含该语句的最内层循环和执行循环表达式(递增/递减循环变量)，然后执行下一次循环。

break 中止包含该语句的最内层循环，并不再继续执行循环。

关于 discard,它只能在片元着色器中使用，表示放弃当前片元直接处理下一个片元。具体使用 discard 的方法将在第 10章“高级技术”中的“绘制圆形点”一节详述

函数

与JavaScript 中函数定义的方式不同，GLSL ES 定义函数的方式更接近于 C 语言其格式如下:

返回类型函数名(typeO arg0， typel argl，...， typen argn) {
    函数计算
    return 返回值;
}

参数的 type 必须为本章所述的类型之一，或者像 main() 函数这样没有参数也是允许的。如果函数不返回值，那么函数中就不需要有 return 语句。但这种情况下，返回类型必须是void。你也可以将自己定义的结构体类型指定为返回类型，但是结构体的成员中不能有数组。

注意，如果调用函数时传人的参数类型与声明函数时指定的参数类型不一致，就会出错。

和 C 和 javascript 不同的是，你不能在一个函数内部调用它本身 (也就是说，递归调用是不允许的)。这项限制的目的也是为了便于编译器对函数进行内联展开。

规范声明

如果函数定义在其调用之后，那么我们必须在进行调用之前先声明该函数的规范。规范声明会预先告诉 WebGL 系统函数的参数、参数类型、返回值等等。这一点与JavaScript 截然不同，后者不需要提前声明函数。

参数限定词

在 GLSL ES 中，可以为函数参数指定限定字，以控制参数的行为。我们可以将函数参数定义成 :(1) 传递给函数的，(2) 将要在函数中被赋值的，(3) 既是传递给函数的，也是将要在函数中被赋值的。其中(2)和(3)都有点类似于 C 语言中的指针。表 6.2 显示了这些参数的限定字。

内置函数

除了允许用户自定义函数，GLSL ES 还提供了很多常用的内置函数。表 6.13 概括了GLSL ES 的内置函数。

全局变量和局部变量

就像 JavaScript和 C 语言，GLSL ES 中也有全局变量和局部变量的概念。全局变量可以在程序中的任意位置使用，而局部变量只能在有限的某一部分代码中使用,

在 GLSL ES 中如果变量声明在函数的外面，那么它就是全局变量，如果声明在函数内部，那就是局部变量。这和 JavaScript 与 C 语言也是一样的。局部变量只能在函数内部使用。

存储限定字

在 GLSL ES 中，我们经常使用 attribute、varying 和 uniform 限定字来修饰变量，如图 6.3所示。此外，我们有时也会使用 const 限定字，它表示着色器中的某个变量是恒定的常量。

const变量

GLSL ES 使用 const 限定字表示该变量的值不能被改变。

在声明 const 变量时，需要将 const 写在类型之前，就像声明 attribute 变量时将attribute 写在前面一样。声明同时必须对它进行初始化，声明之后就不能再去改变它们的值了。

const int lightspeed = 299792458;	// 光速(m/s)
const vec4 red = vec4(1.0，0.0，0.0，1.0);	// 红色
const mat4 identity = mat4(1.0);	// 单位矩阵

试图向 const 变量赋值会导致编译报错

const int lightspeed;
lightspeed = 299792458;

// 错误
failed to compile shader: ERROR: 0:11: "lightspeed' : variables with qualifier 'const' must be initialized
ERROR: 0:12: 'assign': -value required (can't modify a const variable)

Attribute 变量

attribute 变量只能出现在顶点着色器中，只能被声明为全局变量，被用来表示逐顶点的信息。你应该重点理解“逐顶点”的含义。比如，如果线段有两个顶点 (4.0,3.0,6.0)和(8.0,3.0,0.0)，这两个坐标就会传递给 attribute变量。而线段上的其他点，比如中点 (6.0,3.0,3.0)，虽然也被画了出来，但它不是顶点坐标未曾传递给 attribute 变量，也未曾被顶点着色器处理过。如果你想要让顶点着色器处理它，你就需要将它作为一个顶点添加到图形中来。attribute 变量的类型只能是 float、vec2、vec3、vec4、mat2、mat3 和 mat4。

顶点着色器中能够容纳的 attribute 变量的最大数目与设备有关，你可以通过访问内置的全局常量来获取该值 (最大数目)。但是，不管设备配置如何，支持 WebGL 的环境都支持至少 8个 attribute 变量如表 6.14 所示。

uniform 变量

uniform 变量可以用在顶点着色器和片元着色器中，且必须是全局变量。uniform 变量是只读的，它可以是除了数组或结构体之外的任意类型。如果顶点着色器和片元着色器中声明了同名的 uniform 变量,那么它就会被两种着色器共享。uniform 变量包含了致”(非逐顶点/逐片元的，各顶点或各片元共用)的数据，JavaScript应该向其传递此类数据。比如，变换矩阵就不是逐顶点的，而是所有顶点共用的，所以它在着色器中是uniform 变量。

顶点着色器和片元着色器对其中 uniform 变量的数量限制与设备有关，且各不相同如表 6.14 所示。

varying 变量

最后一个限定字是 varying。varying 变量必须是全局变量，它的任务是从顶点着色器向片元着色器传输数据。我们必须在两种着色器中声明同名、同类型的 varying 变量。

和 attribue 变量一样，varying 变量只能是以下类型 : float、vec2vec3vec4mat3 和 mat4。如第 5章所述，顶点着色器中赋给 varying 变量的值并不是直接传给了片元着色器的 varying 变量，这其中发生了光栅化的过程 :根据绘制的图形，对前者(顶点着色器 varying变量)进行内插，然后再传递给后者 (片元着色器 varying 变量)。正是因为 varying 变量需要被内插，所以我们需要限制它的数据类型。

varying 变量的数量限制也与设备有关，至少支持 8 个，如表 6.14 所示

精度限定字

GLSL ES 新引人了精度限定字,目的是帮助着色器程序提高运行效率，削减内存开支。顾名思义，精度限定字用来表示每种数据具有的精度 (比特数)。简而言之，高精度的程序需要更大的开销(包括更大的内存和更久的计算时间)，而低精度的程序需要的开销则小得多。使用精度限定字，你就能精细地控制程序在效果和性能间的平衡。然而，精度限定字是可选的，如果你不确定，可以使用下面这个适中的默认值:

#ifdef GL_ES
	precision mediump float;
#endif

由于webgl是基于opengl es2.0的，webgl程序最后有可能运行在各种个样的硬件平台，肯定存在某些情况需要在低精度下运行程序，以提高内存使用效率，减少性能开销以及更重要的，降低能耗，延长移动设备的电池续航能力。

注意，在低精度下，WebGL 程序的运行结果会比较粗糙或不准确，你必须在程序效果和性能间进行平衡。

如表 6.15 所示，WebGL 程序支持三种精度，其限定字分别为 mediump (中精度) lowp (低精度)和 highp (高精度)。

还有两点值得注意。首先，在某些 WebGL 环境中，片元着色器可能不支持 highp 精度，检查(其是否支持)的方法稍后再讨论，其次，数值范围和精度实际上也是与系统环境相关的，你可以使用 gl.getShaderPrecisionFormat() 来检查。

// 下面是声明变量精度的几个例子 :
mediump float size;	//中精度的浮点型变量
highp vec4 position;	//具有高精度浮点型元素的vec4对象
lowp vec4 color;	// 具有低精度浮点型元素的vec4对象

为每个变量都声明精度很繁琐，我们也可以使用关键字默认精度precision 来声明着色器的默认精度，这行代码必须在顶点着色器或片元着色器的顶部，其格式如下：

precision 精度限定字 类型名称；

这句代码表示，在着色器中某种类型的变量其默认精度由精度限定字指定。也就是说，接下来所有不以精度限定字修饰的该类型变量，其精度就是默认精度。

你也许已经注意到，在前几章我们并没有限定类型的精度 (除了在片元着色器中对float 类型做出限定)。这是因为，对于这些类型，着色器已经实现了默认的精度，只有片元着色器中的 foat 类型没有默认精度。如表 6.16 所示。

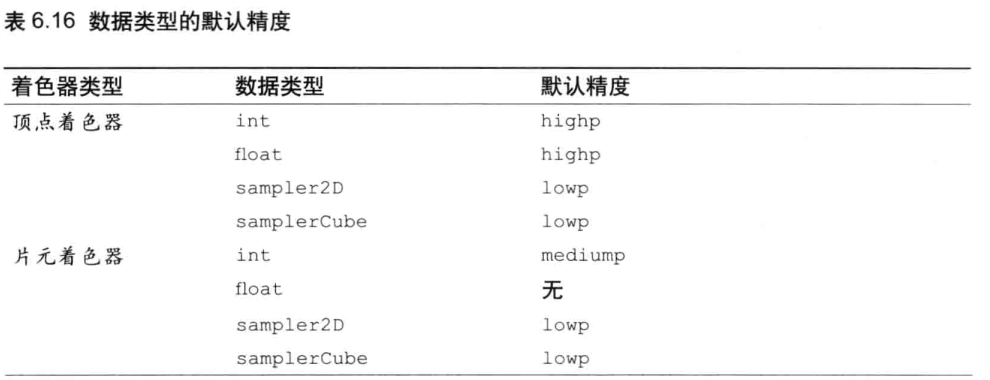
事实就是，片元着色器中的 float 类型没有默认精度，我们需要手动指定。如果我们不在片元着色器中限定 foat 类型的精度，就会导致如下的编译错误

failed to compile shader: ERROR: 0:1 : No precision specified for (float).

我们说过，WebGL 是否在片元着色器中支持 highp 精度，取决于具体的设备。如果其支持的话，那么着色器就会定义内置宏 GL_FRAGMENT_PRECISION_HIGH(见下一节)

预处理指令

GLSL ES 支持预处理指令。预处理指令用来在真正编译之前对代码进行预处理，都以井号 (#)开始。下面就是我们在 coloredPoints.js 中使用的预处理指令

#ifdef GL_ES
	precision mediump float;
#endif

这段代码检查了是否已经定义了 GL_ES 宏，如果是，那就执行 #ifdef 和 #endif 之间的部分。这个预处理指令的格式和 C 语言或 JavaScript 中的 if 语句很类似。

下面是我们在 GLSL ES 中可能用到的三种预处理指令

#if 条件表达式
If 如果条件表达式为真，执行这里
#endif

#ifdef 某宏
如果定义了某宏，执行这里
#endif

#ifndef 某宏
如果没有定义某宏，执行这里
#endif

你可以使用 #define 指令进行宏定义。和C语言中的宏不同，GLSL ES 中的宏没有宏参数 :

#define 宏名 宏内容

你可以使用 #undef 指令解除宏定义 :

 #undef 宏名

你可以使用 #else 指令配合 #ifdef (就像C语言或 JavaScript 中if 语句中的 else),比如 :

 #define NUM 100
 #if NUM == 100
 如果宏NUM为100，执行这里
 #else
 否则，执行这里
 #endif

宏的名称可以任意起，只要不和预定义的内置宏名称 (表 6.17)相同即可。

所以，我们可以这样使用宏来进行精度限定

#ifdef GL_ES
#ifdef GL_FRAGMENT_PRECISION_HIGH
	precision highp float;	// 支持高精度，限定浮点型为高精度
#else
	precision mediump float;	// 不支持高精度，限定浮点型为中精度
#endif
#endif

可以使用 #version 来指定着色器使用的 GLSLES 版本

#version number

可以接受的版本包括 100(GLSL ES 1.00) 和 101 (GLSL ES 1.01)。如果不使用#version 指令，着色器将默认 GLSL ES 的版本是 1.00。指定 1.01 版本的代码如下 :

#version 101

#version 指令必须在着色器顶部，在它之前只能有注释和空白。

进入三维世界

立方体由三角形构成

三维物体是由三角形组成的，那我们只需像前几章那样，逐个绘制组成物体的每个三角形，最终就可以绘制出整个三维物体了。但是，三维与二维还有一个显著区别:在绘制二维图形时，只需要考虑顶点的x和y坐标，而绘制三维物体时，还得考虑它们的深度信息(depth information)。首先我们来研究一下如何定义三维世界的观察者 :在什么地方、朝哪里看、视野有多宽、能看多远。

视点和视线

因此三维物体与二维图形的最显著区别就是，三维物体具有深度，也就是 Z 轴。你会遇到一些之前不曾考虑过的问题。事实上，我们最后还是得把三维场景绘制到二维的屏幕上，即绘制观察者看到的世界，而观察者可以处在任意位置观察。为了定义一个观察者，你需要考虑以下两点 :

观察方向，即观察者自己在什么位置，在看场景的哪一部分?

可视距离，即观察者能够看多远?

我们将观察者所处的位置称为视点(eye point)，从视点出发沿着观察方向的射线称作视线(viewing direction)。

在 WebGL 系统中，默认情况下的视点处于原点(0,0,0)，视线为Z轴负半轴 (指向屏幕内部)。在这一节中，我们把视点从默认位置移动到另一个位置，以观察场景中的三角形。

我们创建来一个新的示例程序 LookAtTriangles。在程序中，视点位于(0.20,0.25.0.25)，视线向着原点(0，，0) 方向，可以看到原点附近有三个三角形。程序中的这三个三角形前后错落摆放，以帮助你理解三维场景中深度的概念。图 7.2 显示了 LookAtTri-angles 的运行结果。

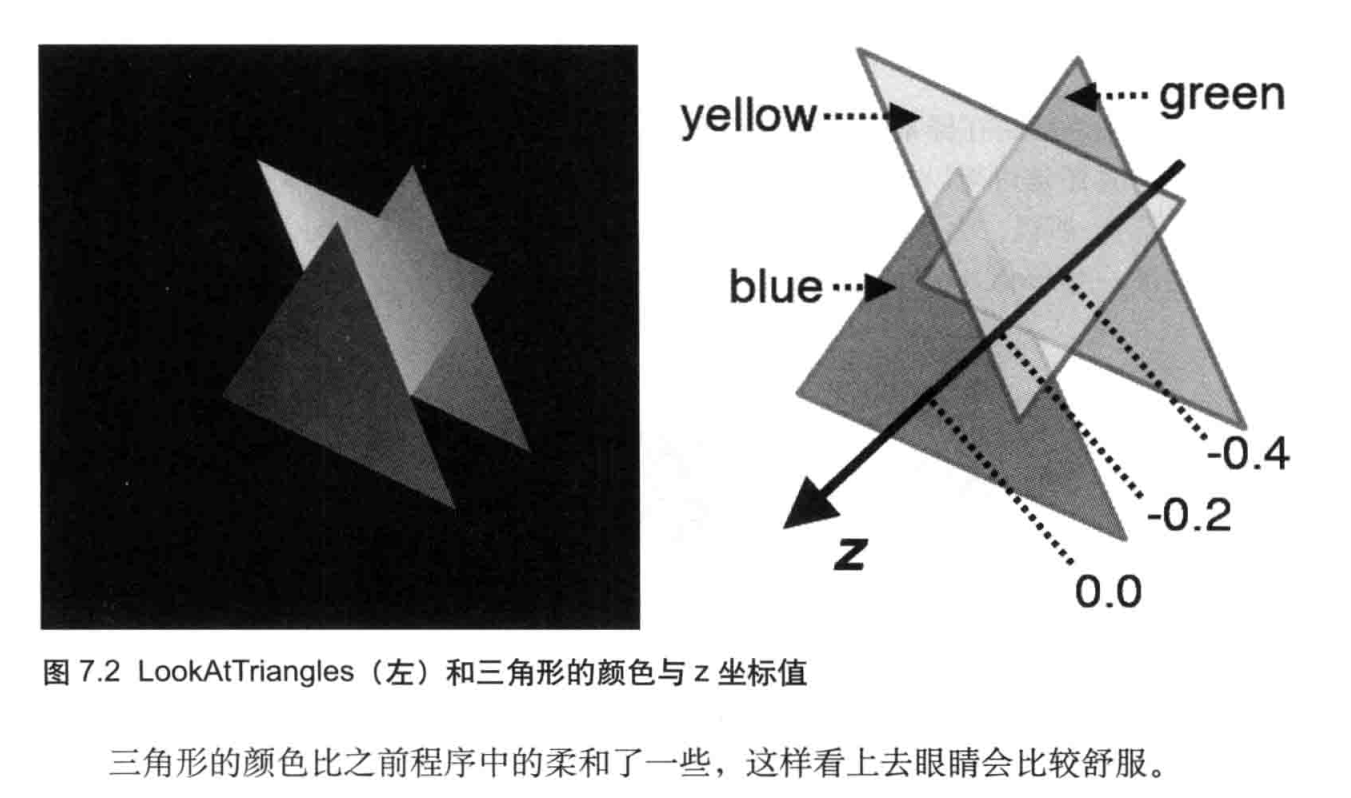
// LookAtTriangles.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'uniform mat4 u_ViewMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_ViewMatrix * a_Position;\n' +
  '  v_Color = a_Color;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // 设置顶点坐标和颜色（蓝色三角形在最前面）
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0, 0, 0, 1);

  // 获取 u_ViewMatrix 变量的存储地址
  var u_ViewMatrix = gl.getUniformLocation(gl.program, 'u_ViewMatrix');
  if (!u_ViewMatrix) { 
    console.log('Failed to get the storage locations of u_ViewMatrix');
    return;
  }

  // 设置视点，视线和上方向
  var viewMatrix = new Matrix4();
  viewMatrix.setLookAt(0.20, 0.25, 0.25, 0, 0, 0, 0, 1, 0);

  // 将视图矩阵传给u_ViewMatrix变量
  gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements);

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);

  // 绘制三角形
  gl.drawArrays(gl.TRIANGLES, 0, n);
}

function initVertexBuffers(gl) {
  var verticesColors = new Float32Array([
    // 顶点坐标和颜色
     0.0,  0.5,  -0.4,  0.4,  1.0,  0.4, // 绿色三角形在最后面
    -0.5, -0.5,  -0.4,  0.4,  1.0,  0.4,
     0.5, -0.5,  -0.4,  1.0,  0.4,  0.4, 
   
     0.5,  0.4,  -0.2,  1.0,  0.4,  0.4, // 黄色三角形在中间
    -0.5,  0.4,  -0.2,  1.0,  1.0,  0.4,
     0.0, -0.6,  -0.2,  1.0,  1.0,  0.4, 

     0.0,  0.5,   0.0,  0.4,  0.4,  1.0,  // 蓝色
    -0.5, -0.5,   0.0,  0.4,  0.4,  1.0,
     0.5, -0.5,   0.0,  1.0,  0.4,  0.4, 
  ]);
  var n = 9;

  // Create a buffer object
  var vertexColorbuffer = gl.createBuffer();  
  if (!vertexColorbuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // Write the vertex coordinates and color to the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorbuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);

  var FSIZE = verticesColors.BYTES_PER_ELEMENT;
  // Assign the buffer object to a_Position and enable the assignment
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if(a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0);
  gl.enableVertexAttribArray(a_Position);

  // Assign the buffer object to a_Color and enable the assignment
  var a_Color = gl.getAttribLocation(gl.program, 'a_Color');
  if(a_Color < 0) {
    console.log('Failed to get the storage location of a_Color');
    return -1;
  }
  gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3);
  gl.enableVertexAttribArray(a_Color);

  // Unbind the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, null);

  return n;
}

视点、观察目标点和上方向

为了确定观察者的状态，你需要获取两项信息:视点，即观察者的位置；观察目标点 (look-at point)，即被观察目标所在的点，它可以用来确定视线。此外，因为我们最后点,要把观察到的景象绘制到屏幕上，还需要知道上方向(up direction)。有了这三项信息就可以确定观察者的状态了。下面将逐一进行解释 (见图 7.3)。

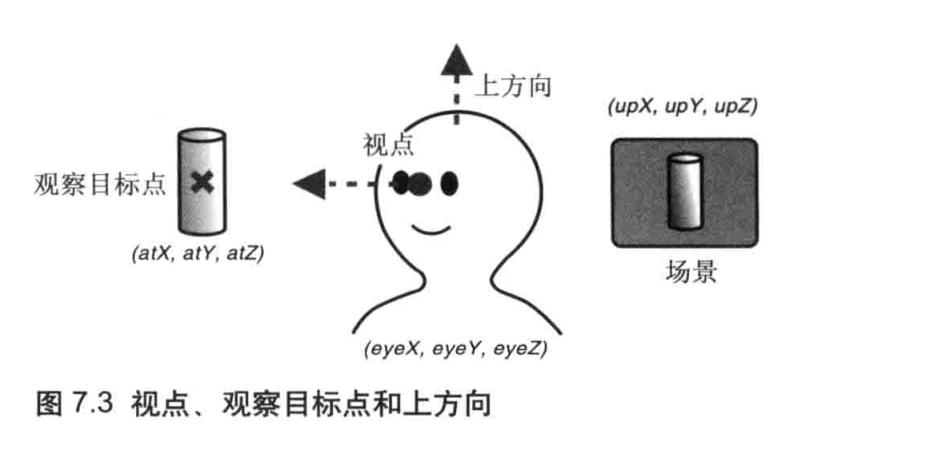
视点：观察者所在的三维空间中位置，视线的起点。在接下来的几节中，视点坐标都用(eyeX，eyeY，eyeZ)表示。

观察目标点：被观察目标所在的点。视线从视点出发，穿过观察目标点并继续延伸。注意观察目标点是一个点，而不是视线方向，只有同时知道观察目标点和视点，才能算出视线方向。观察目标点的坐标用(atX，atY，atz) 表示。

上方向：最终绘制在屏幕上的影像中的向上的方向。试想，如果仅仅确定了视点和观察点，观察者还是可能以视线为轴旋转的(如图 7.4 所示，头部偏移会导致观察到的场景也偏移了)。所以，为了将观察者固定住，我们还需要指定上方向。上方向是具有 3个分量的矢量，用 (upX, upY,upZ) 表示。

在 WebGL 中，我们可以用上述三个矢量创建一个视图矩阵(view matrix)，然后将该矩阵传给顶点着色器。视图矩阵可以表示观察者的状态，含有观察者的视点，观察目标点、上方向等信息。之所以被称为视图矩阵，是因为它最终影响了显示在屏幕上的视图，也就是观察者观察到的场景。

本书中的cuon-matrix.js 提供的 Matrix4.setLookAt() 函数可以根据上述三个矢量：视点、观察点和上方向，来创建出视图矩阵。

在 WebGL 中，观察者的默认状态应该是这样的 :

视点位于坐标系统原点(0,0,0)。

视线为Z轴负方向，观察点为(0,0,-1)，上方向为Y轴负方向，即(0,1,0)。

如果将上方向改为 X轴正半轴方向(1,0,0)，你将看到场景旋转了 90 度。

创建这样一个矩阵，你只需要简单地使用如下代码

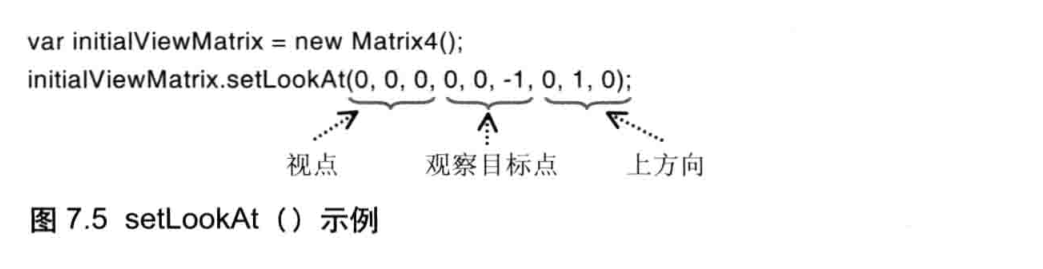
实际上，“根据自定义的观察者状态，绘制观察者看到的景象”与“使用默认的观察状态，但是对三维对象进行平移、旋转等变换，再绘制观察者看到的景象”，这两种行为是等价的。

举个例子，默认情况下视点在原点，视线沿着Z轴负方向进行观察。假如我们将视点移动到(0,0,1)，如图7.6(左)所示。这时，视点与被观察的三角形在Z轴上的距离增加了10个单位。实际上，如果我们使三角形沿Z轴负方向移动10个单位，也可以达到同样的效果，因为观察者看上去是一样的，如图 7.6(右)所示。

事实上，上述过程就发生在示例程序LookAtTrianglesjs中。根据视点、观察点和上方向参数，setLookAt()方法计算出的视图矩阵恰恰就是“沿着Z轴负方向移动1.0个单位”的变换矩阵。所以，把这个矩阵与顶点坐标相乘，就相当于获得了“将视点设置在(0.0，0.0，1.0)”的效果。视点移动的方向与被观察对象(也就是整个世界)移动的方向正好相反。对于视点的旋转，也可以采用类似的方式。

“改变观察者的状态”与“对整个世界进行平移和旋转变换”，本质上是一样的，它们都可以用矩阵来描述。接下来，我们将从一个指定的视点来观察旋转后的三角形。

从指定视点观察旋转后的三角形

第4章RotatedTriangleMatrix程序绘制了一个绕Z轴旋转一定角度后的三角形。本节将修改LookAtTriangles程序来绘制一个从指定位置看过去的旋转后的三角形。这时，我们需要两个矩阵:旋转矩阵(表示三角形的旋转)和视图矩阵(表示观察世界的方式)。首先有一个问题是，以怎样的顺序相乘这两个矩阵。

我们知道，矩阵乘以顶点坐标，得到的结果是顶点经过矩阵变换之后的新坐标。也就是说，用旋转矩阵乘以顶点坐标，就可以得到旋转后的顶点坐标。

用视图矩阵乘以顶点坐标会把顶点变换到合适的位置，使得观察者(以默认状态观察新位置的顶点，就好像在观察者处在(视图矩阵描述的)视点上观察原始顶点一样。现在要在某个视点处观察旋转后的三角形，我们需要先旋转三角形，然后从这个视点来观察它。换句话说，我们需要先对三角形进行旋转变换，再对旋转后的三角形进行与“移动视点”等效的变换。我们按照上述顺序相乘两个矩阵。具体看一下等式。

我们知道，如果想旋转图形，就需要用旋转矩阵乘以旋转前的顶点坐标:
<旋转后顶点坐标>=<旋转矩阵>x<原始顶点坐标>

用视图矩阵乘以旋转后的顶点坐标，就可以获得“从视点看上去”的旋转后的顶点坐标:
<“从视点看上去”的旋转后顶点坐标>=<视图矩阵>x<旋转后顶点坐标>

将第1个式子代入第2个，可得:
<“从视点看上去”的旋转后顶点坐标>=<视图矩阵>x<旋转矩阵>x<原始顶点坐标>

除了旋转矩阵，你还可以使用平移、缩放等基本变换矩阵或它们的组合，这时矩阵被称为模型矩阵(modelmatrix)。这样，上式就可以写成:

// LookAtRotatedTriangles.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'uniform mat4 u_ViewMatrix;\n' +
  'uniform mat4 u_ModelMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_ViewMatrix * u_ModelMatrix * a_Position;\n' +
  '  v_Color = a_Color;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex coordinates and color (the blue triangle is in the front)
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0.0, 0.0, 0.0, 1.0);

  // Get the storage location of u_ViewMatrix and u_ModelMatrix
  var u_ViewMatrix = gl.getUniformLocation(gl.program, 'u_ViewMatrix');
  var u_ModelMatrix = gl.getUniformLocation(gl.program, 'u_ModelMatrix');
  if(!u_ViewMatrix || !u_ModelMatrix) { 
    console.log('Failed to get the storage location of u_viewMatrix or u_ModelMatrix');
    return;
  }

  // Set the matrix to be used for to set the camera view
  var viewMatrix = new Matrix4();
  viewMatrix.setLookAt(0.20, 0.25, 0.25, 0, 0, 0, 0, 1, 0);

  // Calculate matrix for rotate
  var modelMatrix = new Matrix4();
  modelMatrix.setRotate(-10, 0, 0, 1); // Rotate around z-axis

  // Pass the view projection matrix and model matrix
  gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements);
  gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements);

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);

  // Draw the rectangle
  gl.drawArrays(gl.TRIANGLES, 0, n);
}

function initVertexBuffers(gl) {
  var verticesColors = new Float32Array([
    // Vertex coordinates and color
     0.0,  0.5,  -0.4,  0.4,  1.0,  0.4, // The back green one
    -0.5, -0.5,  -0.4,  0.4,  1.0,  0.4,
     0.5, -0.5,  -0.4,  1.0,  0.4,  0.4, 
   
     0.5,  0.4,  -0.2,  1.0,  0.4,  0.4, // The middle yellow one
    -0.5,  0.4,  -0.2,  1.0,  1.0,  0.4,
     0.0, -0.6,  -0.2,  1.0,  1.0,  0.4, 

     0.0,  0.5,   0.0,  0.4,  0.4,  1.0,  // The front blue one 
    -0.5, -0.5,   0.0,  0.4,  0.4,  1.0,
     0.5, -0.5,   0.0,  1.0,  0.4,  0.4, 
  ]);
  var n = 9;

  // Create a buffer object
  var vertexColorBuffer = gl.createBuffer();  
  if (!vertexColorBuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // Write vertex information to buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorBuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);

  var FSIZE = verticesColors.BYTES_PER_ELEMENT;
  // Assign the buffer object to a_Color and enable the assignment
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if(a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0);
  gl.enableVertexAttribArray(a_Position);
  // Assign the buffer object to a_Color and enable the assignment
  var a_Color = gl.getAttribLocation(gl.program, 'a_Color');
  if(a_Color < 0) {
    console.log('Failed to get the storage location of a_Color');
    return -1;
  }
  gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3);
  gl.enableVertexAttribArray(a_Color);

  // Unbind the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, null);

  return n;
}

运行示例程序，顶点坐标依次与旋转矩阵和视图矩阵相乘，最终获得了预期的效果。如图7.6所示，即先用u_ModelMatrix旋转三角形，再将旋转后的坐标用u_ViewMatrix变换到正确的位置，使其看上去就像是从指定视点处观察一样。

在LookAtRotatedTrianglejs中，着色器实现了式7.1（视图矩阵x模型矩阵x原始坐标)。这样，程序对每个顶点都要计算视图矩阵x模型矩阵。如果顶点数量很多，这一步操作就会造成不必要的开销。这是因为，无论对哪个顶点而言，式7.1中的两个矩阵相乘的结果都是一样的。所以我们可以在JavaScript中事先把这两个矩阵相乘的结果计算出来,再传给顶点着色器。这两个矩阵相乘得到的结果被称为模型视图矩阵(modelview matrix)，如下所示:

<模型视图矩阵>=<视图矩阵>x<模型矩阵>

这样，式7.1可以重写为式7.2:

利用键盘改变视点

// LookAtTrianglesWithKeys.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'uniform mat4 u_ViewMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_ViewMatrix * a_Position;\n' +
  '  v_Color = a_Color;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex coordinates and color (the blue triangle is in the front)
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0, 0, 0, 1);

  // Get the storage location of u_ViewMatrix
  var u_ViewMatrix = gl.getUniformLocation(gl.program, 'u_ViewMatrix');
  if(!u_ViewMatrix) { 
    console.log('Failed to get the storage locations of u_ViewMatrix');
    return;
  }

  // Create the view matrix
  var viewMatrix = new Matrix4();
  // 注册键盘事件响应函数
  document.onkeydown = function(ev){ keydown(ev, gl, n, u_ViewMatrix, viewMatrix); };

  draw(gl, n, u_ViewMatrix, viewMatrix);   // Draw
}

function initVertexBuffers(gl) {
  var verticesColors = new Float32Array([
    // Vertex coordinates and color
     0.0,  0.5,  -0.4,  0.4,  1.0,  0.4, // The back green one
    -0.5, -0.5,  -0.4,  0.4,  1.0,  0.4,
     0.5, -0.5,  -0.4,  1.0,  0.4,  0.4, 
   
     0.5,  0.4,  -0.2,  1.0,  0.4,  0.4, // The middle yellow one
    -0.5,  0.4,  -0.2,  1.0,  1.0,  0.4,
     0.0, -0.6,  -0.2,  1.0,  1.0,  0.4, 

     0.0,  0.5,   0.0,  0.4,  0.4,  1.0,  // The front blue one 
    -0.5, -0.5,   0.0,  0.4,  0.4,  1.0,
     0.5, -0.5,   0.0,  1.0,  0.4,  0.4, 
  ]);
  var n = 9;

  // Create a buffer object
  var vertexColorbuffer = gl.createBuffer();  
  if (!vertexColorbuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // Write the vertex information and enable it
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorbuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);

  var FSIZE = verticesColors.BYTES_PER_ELEMENT;
  //Get the storage location of a_Position, assign and enable buffer
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if(a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }

  gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0);
  gl.enableVertexAttribArray(a_Position);  // Enable the assignment of the buffer object

  // Get the storage location of a_Position, assign buffer and enable
  var a_Color = gl.getAttribLocation(gl.program, 'a_Color');
  if(a_Color < 0) {
    console.log('Failed to get the storage location of a_Color');
    return -1;
  }
  // Assign the buffer object to a_Color variable
  gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3);
  gl.enableVertexAttribArray(a_Color);  // Enable the assignment of the buffer object

  return n;
}

var g_eyeX = 0.20, g_eyeY = 0.25, g_eyeZ = 0.25; // 视点
function keydown(ev, gl, n, u_ViewMatrix, viewMatrix) {
    if(ev.keyCode == 39) { // 按下右键
      g_eyeX += 0.01;
    } else 
    if (ev.keyCode == 37) { // 按下左键
      g_eyeX -= 0.01;
    } else { return; }
    draw(gl, n, u_ViewMatrix, viewMatrix);    
}

function draw(gl, n, u_ViewMatrix, viewMatrix) {
  // 设置视点和视线
  viewMatrix.setLookAt(g_eyeX, g_eyeY, g_eyeZ, 0, 0, 0, 0, 1, 0);

  // Pass the view projection matrix
  gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements);

  gl.clear(gl.COLOR_BUFFER_BIT);     // Clear <canvas>

  gl.drawArrays(gl.TRIANGLES, 0, n); // Draw the rectangle
}

在本例中，我们注册了键盘事件响应函数。每当左方向键或右方向键被按下时，就改变视点的位置，然后调用 draw()函数重绘场景。

独缺一角

如果你仔细观察示例程序的运行效果，就会注意到当视点在极右或极左的位置时三角形会缺少一部分，如图 7.9 所示。

三角形缺了一角的原因是，我们没有指定可视范围 (visible range)即实际观察得到的区域边界。如前一章所述,WebGL 只显示可视范围内的区域。例中当我们改变视点位置时，三角形的一部分到了可视范围外，所以图 7.9 中的三角形就缺了一个角。

可视范围（正射类型）

虽然你可以将三维物体放在三维空间中的任何地方，但是只有当它在可视范围内时，WebGL 才会绘制它。事实上，不绘制可视范围外的对象，是基本的降低程序开销的手段。绘制可视范围外的对象没有意义，即使把它们绘制出来也不会在屏幕上显示。从某种程序上来说，这样做也模拟了人类观察物体的方式，如图 7.10 所示。我们人类也只能看到眼前的东西，水平视角大约 200 度左右。总之，WebGL 就是以类似的方式，只绘制可视范围内的三维对象。

除了水平和垂直范围内的限制，WebGL 还限制观察者的可视深度,即“能够看多远”。所有这些限制，包括水平视角、垂直视角和可视深度，定义了可视空间(view volume)。由于我们没有显式地指定可视空间，默认的可视深度又不够远，所以三角形的一个角看上去就消失了，如图 7.9 所示

可视空间

有两类常用的可视空间 :

长方体可视空间，也称盒状空间，由正射投影(orthographic projection)产生。

四棱锥 /金字塔可视空间，由透视投影(perspective projection)产生。

在透视投影下，产生的三维场景看上去更是有深度感，更加自然，因为我们平时观察真实世界用的也是透视投影。在大多数情况下，比如三维射击类游戏中，我们都应当采用透视投影。相比之下，正射投影的好处是用户可以方便地比较场景中物体 (比如两个原子的模型)的大小，这是因为物体看上去的大小与其所在的位置没有关系。在建筑平面图等技术绘图的相关场合，应当使用这种投影。

首先介绍基于正射投影的盒状可视空间的工作原理

盒状可视空间的形状如图 7.11 所示。可视空间由前后两个矩形表面确定，分别称近裁剪面(near clipping plane)和远裁剪面(far clipping plane)，前者的四个顶点为(right,top-near),(-left, top, -near)，(-left, --bottom, -near),(right, -bottom, -near)，而后者的四个顶点为 (right, top, far),(-left, top, far),(-left, --bottom, far) ,(right, --bottom, far).

canvas上显示的就是可视空间中物体在近裁剪面上的投影。如果裁剪面的宽高比和canvas不一样,那么画面就会被按照canvas 的宽高比进行压缩,物体会被扭曲，近裁剪面与远裁剪面之间的盒形空间就是可视空间，只有在此空间内的物体会被显示出来。如果某个物体一部分在可视空间内，部分在其外，那就只显示空间内的部分。

定义盒状可视空间

本书中的 cuon-matrix.js 提供的Matrix4setOrtho()方法可用来设置投影矩阵，定义盒装可视空间。

这里得到一个矩阵。这个矩阵被称为正射投影矩阵(orthographicprojectionmatrix)。示例程序OrthoView将使用这种矩阵定义盒状可视空间，并绘制3个与LookA-tRotatedTriangles中一样的三角形，由此测试盒状可视空间的效果。LookAtRotatedTri-angles程序将视点放在一个指定的非原点位置上，但本例为方便，直接把视点置于原点处，视线为Z轴负方向。可视空间定义如图7.12所示，near=0.0，far=0.5，left=-1.0.right=1.0，bottom=-10，top=10，三角形处于Z轴00到-0.4区间上。

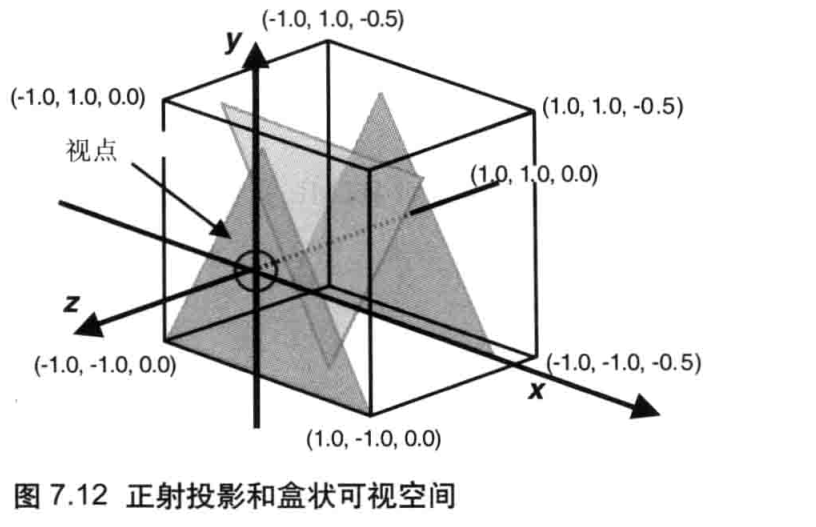
此外，示例程序还允许通过键盘按键修改可视空间的near和far值。这样我们就能直观地看到这两个值具体对可视空间有什么影响。

// OrthoView.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'uniform mat4 u_ProjMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_ProjMatrix * a_Position;\n' +
  '  v_Color = a_Color;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');
  // Retrieve the nearFar element
  var nf = document.getElementById('nearFar');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex coordinates and color (the blue triangle is in the front)
  var n =  initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0, 0, 0, 1);

  // get the storage location of u_ProjMatrix
  var u_ProjMatrix = gl.getUniformLocation(gl.program, 'u_ProjMatrix');
  if (!u_ProjMatrix) { 
    console.log('Failed to get the storage location of u_ProjMatrix');
    return;
  }

  // Create the matrix to set the eye point, and the line of sight
  var projMatrix = new Matrix4();
  // Register the event handler to be called on key press
  document.onkeydown = function(ev){ keydown(ev, gl, n, u_ProjMatrix, projMatrix, nf); };

  draw(gl, n, u_ProjMatrix, projMatrix, nf);   // Draw the triangles
}

function initVertexBuffers(gl) {
  var verticesColors = new Float32Array([
    // Vertex coordinates and color
     0.0,  0.6,  -0.4,  0.4,  1.0,  0.4, // The back green one
    -0.5, -0.4,  -0.4,  0.4,  1.0,  0.4,
     0.5, -0.4,  -0.4,  1.0,  0.4,  0.4, 
   
     0.5,  0.4,  -0.2,  1.0,  0.4,  0.4, // The middle yellow one
    -0.5,  0.4,  -0.2,  1.0,  1.0,  0.4,
     0.0, -0.6,  -0.2,  1.0,  1.0,  0.4, 

     0.0,  0.5,   0.0,  0.4,  0.4,  1.0, // The front blue one 
    -0.5, -0.5,   0.0,  0.4,  0.4,  1.0,
     0.5, -0.5,   0.0,  1.0,  0.4,  0.4, 
  ]);
  var n = 9;

  // Create a buffer object
  var vertexColorbuffer = gl.createBuffer();  
  if (!vertexColorbuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // Write the vertex coordinates and color to the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorbuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);

  var FSIZE = verticesColors.BYTES_PER_ELEMENT;
  // Assign the buffer object to a_Position and enable the assignment
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if(a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0);
  gl.enableVertexAttribArray(a_Position);
  // Assign the buffer object to a_Color and enable the assignment
  var a_Color = gl.getAttribLocation(gl.program, 'a_Color');
  if(a_Color < 0) {
    console.log('Failed to get the storage location of a_Color');
    return -1;
  }
  gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3);
  gl.enableVertexAttribArray(a_Color);

  return n;
}

// The distances to the near and far clipping plane
var g_near = 0.0, g_far = 0.5;
function keydown(ev, gl, n, u_ProjMatrix, projMatrix, nf) {
  switch(ev.keyCode){
    case 39: g_near += 0.01; break;  // The right arrow key was pressed
    case 37: g_near -= 0.01; break;  // The left arrow key was pressed
    case 38: g_far += 0.01;  break;  // The up arrow key was pressed
    case 40: g_far -= 0.01;  break;  // The down arrow key was pressed
    default: return; // Prevent the unnecessary drawing
  }
 
  draw(gl, n, u_ProjMatrix, projMatrix, nf);    
}

function draw(gl, n, u_ProjMatrix, projMatrix, nf) {
  // Specify the viewing volume
  projMatrix.setOrtho(-1.0, 1.0, -1.0, 1.0, g_near, g_far);

  // Pass the projection matrix to u_ProjMatrix
  gl.uniformMatrix4fv(u_ProjMatrix, false, projMatrix.elements);

  gl.clear(gl.COLOR_BUFFER_BIT);       // Clear <canvas>

  // Display the current near and far values
  nf.innerHTML = 'near: ' + Math.round(g_near * 100)/100 + ', far: ' + Math.round(g_far*100)/100;

  gl.drawArrays(gl.TRIANGLES, 0, n);   // Draw the triangles
}

运行程序，按下右方向键逐渐增加near值，你会看到三角形逐个消失了。

默认情况下，near值为0.0，此时3个三角形都出现了。当我们首次按下右方向键，将near值增加至0.01时，处在最前面的蓝色的三角形消失了。这是因为，蓝色三角形就在XY平面上，近裁剪面越过了蓝色三角形，使其处在了可视空间外。

我们接着继续增大near值，当near值大于0.2时，近裁剪面越过了黄色三角形，使其处在可视空间外。黄色三角形也消失了，视野中只剩下绿色三角形。此时，如果你逐渐减小near值使其小于0.2，黄色的三角形就会重新出现，而如果继续增大near值使其大于0.4，绿色的三角形就会消失，视野中将空无一物，只剩下黑色的背景。

同样，如果你改变far的值，也会产生类似的效果。随着far值的逐渐减小，当值小于0.4时，绿色三角形首先消失，小于0.2时，黄色三角形消失，最终只剩下蓝色三角形。

这个示例程序清晰地展示了可视空间的作用。如果你想绘制任何东西，就必须把它置于可视空间中。

补上缺掉的角（LookAtTrianglesWithKeys_ViewVolume.js）

在LookAtTrianglesWithKeys中，当你多次按下左或右方向键，处于极左处或极右处观察三角形时，会发现三角形看上去缺了一个角，如图7.17所示。通过前一节的讨论，我们已经很明确地知道这是因为三角形的一部分位于可视区域之外，被裁剪掉了。这一节，我们就来修改程序，适当地设置可视空间，确保三角形不被裁剪。

从上图中可以看出，三角形中距离视点最远的角被裁剪了。显然，这是由远裁剪面过于接近视点导致，我们只需要将远裁剪面移到距离视点更远的地方。为此，我们可以按照以下的配置来修改可视空间:left=-10，right=10，bottom=-1.0，top=1.0，near-0.0，far=2.0。

程序涉及两个矩阵:关于可视空间的正射投影矩阵，以及关于视点与视线的视图矩阵。在顶点着色器中，我们需要用视图矩阵乘以顶点坐标，得到顶点在视图坐标系下的坐标，再左乘正射投影矩阵并赋值给gl_Position。计算过程如式7.3所示。

// LookAtTrianglesWithKey_ViewVolume.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'uniform mat4 u_ViewMatrix;\n' +
  'uniform mat4 u_ProjMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_ProjMatrix * u_ViewMatrix * a_Position;\n' +
  '  v_Color = a_Color;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex coordinates and color (the blue triangle is in the front)
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to specify the vertex infromation');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0.0, 0.0, 0.0, 1.0);

  // Get the storage locations of u_ViewMatrix and u_ProjMatrix variables
  var u_ViewMatrix = gl.getUniformLocation(gl.program, 'u_ViewMatrix');
  var u_ProjMatrix = gl.getUniformLocation(gl.program, 'u_ProjMatrix');
  if (!u_ViewMatrix || !u_ProjMatrix) { 
    console.log('Failed to get u_ViewMatrix or u_ProjMatrix');
    return;
  }

  // Create the matrix to specify the view matrix
  var viewMatrix = new Matrix4();
  // Register the event handler to be called on key press
 document.onkeydown = function(ev){ keydown(ev, gl, n, u_ViewMatrix, viewMatrix); };

  // Create the matrix to specify the viewing volume and pass it to u_ProjMatrix
  var projMatrix = new Matrix4();
  projMatrix.setOrtho(-1.0, 1.0, -1.0, 1.0, 0.0, 2.0);
  gl.uniformMatrix4fv(u_ProjMatrix, false, projMatrix.elements);

  draw(gl, n, u_ViewMatrix, viewMatrix);   // Draw the triangles
}

function initVertexBuffers(gl) {
  var verticesColors = new Float32Array([
    // Vertex coordinates and color
     0.0,  0.5,  -0.4,  0.4,  1.0,  0.4, // The back green one
    -0.5, -0.5,  -0.4,  0.4,  1.0,  0.4,
     0.5, -0.5,  -0.4,  1.0,  0.4,  0.4, 
   
     0.5,  0.4,  -0.2,  1.0,  0.4,  0.4, // The middle yellow one
    -0.5,  0.4,  -0.2,  1.0,  1.0,  0.4,
     0.0, -0.6,  -0.2,  1.0,  1.0,  0.4, 

     0.0,  0.5,   0.0,  0.4,  0.4,  1.0,  // The front blue one 
    -0.5, -0.5,   0.0,  0.4,  0.4,  1.0,
     0.5, -0.5,   0.0,  1.0,  0.4,  0.4, 
  ]);
  var n = 9;

  // Create a buffer object
  var vertexColorbuffer = gl.createBuffer();  
  if (!vertexColorbuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // Write vertex information to buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorbuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);

  var FSIZE = verticesColors.BYTES_PER_ELEMENT;
  // Assign the buffer object to a_Position and enable the assignment
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if(a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0);
  gl.enableVertexAttribArray(a_Position);
  // Assign the buffer object to a_Color and enable the assignment
  var a_Color = gl.getAttribLocation(gl.program, 'a_Color');
  if(a_Color < 0) {
    console.log('Failed to get the storage location of a_Color');
    return -1;
  }
  gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3);
  gl.enableVertexAttribArray(a_Color);

  return n;
}

var g_EyeX = 0.20, g_EyeY = 0.25, g_EyeZ = 0.25; // Eye position
function keydown(ev, gl, n, u_ViewMatrix, viewMatrix) {
    if(ev.keyCode == 39) { // The right arrow key was pressed
      g_EyeX += 0.01;
    } else 
    if (ev.keyCode == 37) { // The left arrow key was pressed
      g_EyeX -= 0.01;
    } else { return; } // Prevent the unnecessary drawing
    draw(gl, n, u_ViewMatrix, viewMatrix);    
}

function draw(gl, n, u_ViewMatrix, viewMatrix) {
  // Set the matrix to be used for to set the camera view
  viewMatrix.setLookAt(g_EyeX, g_EyeY, g_EyeZ, 0, 0, 0, 0, 1, 0);

  // Pass the view projection matrix
  gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements);

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);

  // Draw the rectangle
  gl.drawArrays(gl.TRIANGLES, 0, n);
}

在计算正射投影矩阵projMatrix时，我们将far的值从1.0改成2.0，将结果传给了顶点着色器中的u_ProjMatrix(第67行)。投影矩阵与顶点无关，所以它是uniform变量。运行示例程序，然后像之前那样移动视点，你会发现三角形再也不会被裁剪了。

可视空间（透视投影）

在图7.20的场景中，道路两边都有成排的树木。树应该都是差不多高的，但是在照片上，越远的树看上去越矮。同样，道路尽头的建筑看上去比近处的树矮，但实际上那座建筑比树高很多。这种“远处的东西看上去小”的效果赋予了照片深度感，或称透视感。我们的眼睛就是这样观察世界的。有趣的是，孩童的绘画往往会忽视这一点。

在正射投影的可视空间中，不管三角形与视点的距离是远是近，它有多大，那么画出来就有多大。为了打破这条限制，我们可以使用透视投影可视空间，它将使场景具有图7.20那样的深度感。

示例程序PerspectiveView就使用了一个透视投影可视空间，视点在(0,0,5)，视线沿着Z轴负方向。图7.21显示了程序的运行效果，以及程序的场景中各三角形的位置。

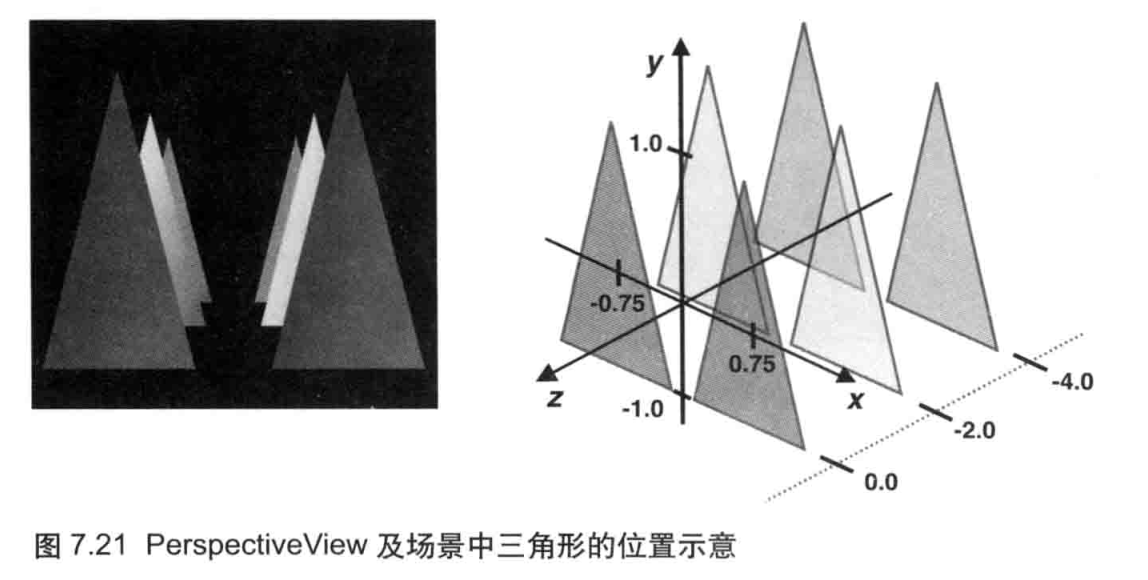
如上图(右)所示，沿着Z轴负半轴(也就是视线方向)，在轴的左右侧各依次排列着3个相同大小的三角形，场景与图7.20中的道路和树木有一点相似。在使用透视投影矩阵后，WebGL 就能够自动将距离远的物体缩小显示，从而产生上图(左)中的深度感。

定义透视投影可视空间

透视投影可视空间如图7.22所示。就像盒状可视空间那样，透视投影可视空间也有视点、视线、近裁剪面和远裁剪面，这样可视空间内的物体才会被显示，可视空间外的物体则不会显示。那些跨越可视空间边界的物体则只会显示其在可视空间内的部分。

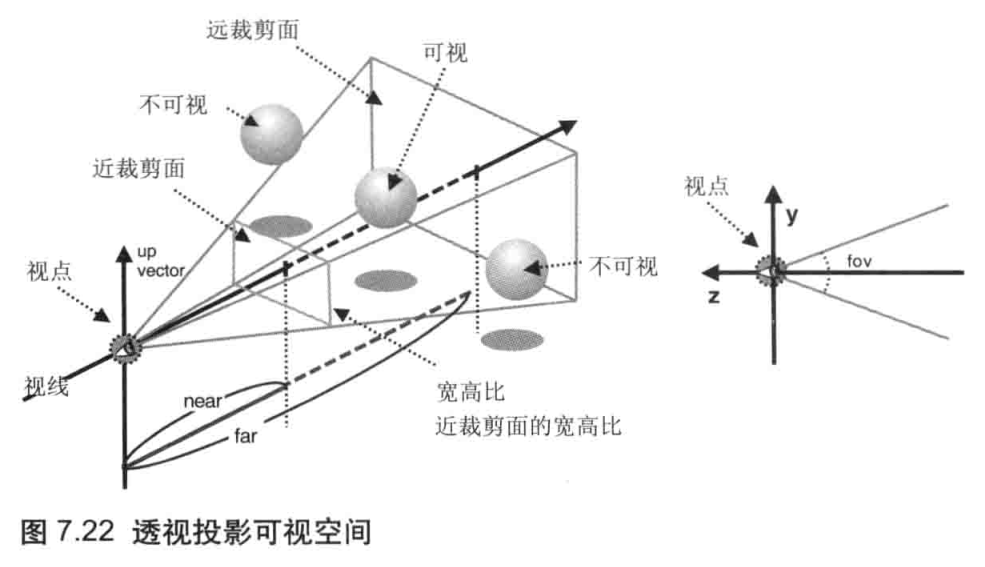
不论是透视投影可视空间还是盒状可视空间，我们都用投影矩阵来表示它，但是定义矩阵的参数不同Matrix4对象(本书中的 cuon-matrix.js 库)的setPerspective()方法可用来定义透视投影可视空间。

定义了透视投影可视空间的矩阵被称为透视投影矩阵(perspective projection matrix)。

注意，第2个参数aspect是近裁剪面的宽高比，而不是水平视角(第1个参数是垂直视角)。比如说，如果近裁剪面的高度是100而宽度是200，那么宽高比就是2。

在本例中,各个三角形与可视空间的相对位置如图7.23所示。我们指定了near=1.0，far=100，aspect=1.0(宽度等于高度，与画面相同)，以及fov=30.0。

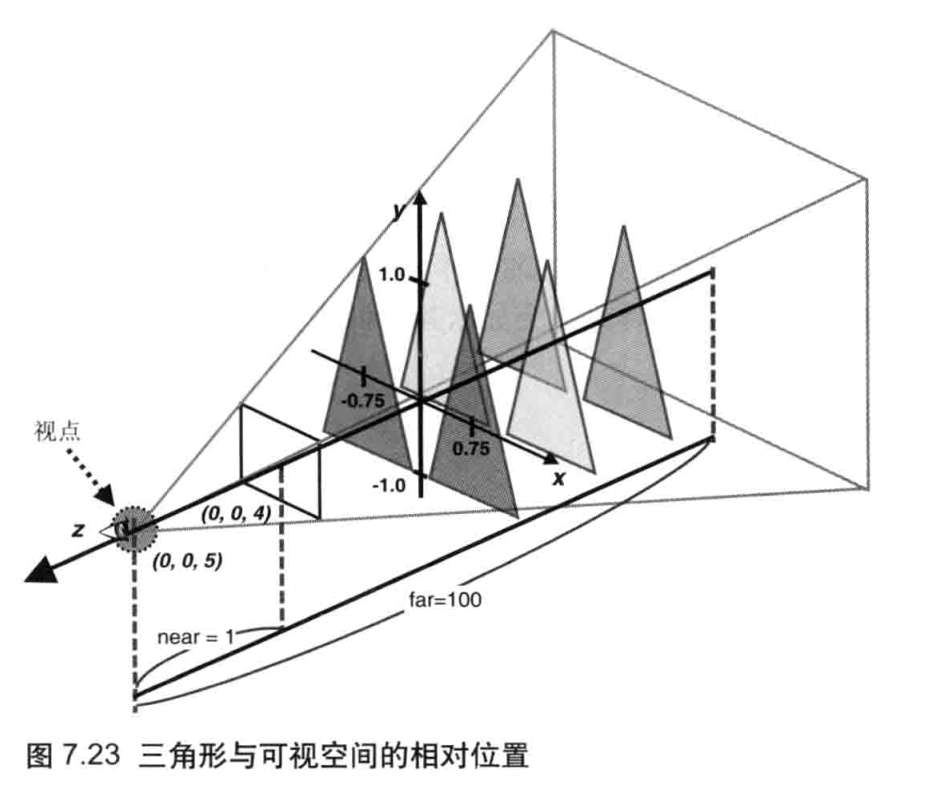
// PerspectiveView.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'uniform mat4 u_ViewMatrix;\n' +
  'uniform mat4 u_ProjMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_ProjMatrix * u_ViewMatrix * a_Position;\n' +
  '  v_Color = a_Color;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex coordinates and color (the blue triangle is in the front)
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0, 0, 0, 1);

  // get the storage locations of u_ViewMatrix and u_ProjMatrix
  var u_ViewMatrix = gl.getUniformLocation(gl.program, 'u_ViewMatrix');
  var u_ProjMatrix = gl.getUniformLocation(gl.program, 'u_ProjMatrix');
  if (!u_ViewMatrix || !u_ProjMatrix) { 
    console.log('Failed to get the storage location of u_ViewMatrix and/or u_ProjMatrix');
    return;
  }

  var viewMatrix = new Matrix4();　// 视图矩阵
  var projMatrix = new Matrix4();  // 投影矩阵

  // 计算视图矩阵和投影矩阵
  viewMatrix.setLookAt(0, 0, 5, 0, 0, -100, 0, 1, 0);
  projMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);
  // Pass the view and projection matrix to u_ViewMatrix, u_ProjMatrix
  gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements);
  gl.uniformMatrix4fv(u_ProjMatrix, false, projMatrix.elements);

  // Clear <canvas>
  gl.clear(gl.COLOR_BUFFER_BIT);

  // Draw the triangles
  gl.drawArrays(gl.TRIANGLES, 0, n);
}

function initVertexBuffers(gl) {
  var verticesColors = new Float32Array([
    // Three triangles on the right side
    0.75,  1.0,  -4.0,  0.4,  1.0,  0.4, // The back green one
    0.25, -1.0,  -4.0,  0.4,  1.0,  0.4,
    1.25, -1.0,  -4.0,  1.0,  0.4,  0.4, 

    0.75,  1.0,  -2.0,  1.0,  1.0,  0.4, // The middle yellow one
    0.25, -1.0,  -2.0,  1.0,  1.0,  0.4,
    1.25, -1.0,  -2.0,  1.0,  0.4,  0.4, 

    0.75,  1.0,   0.0,  0.4,  0.4,  1.0,  // The front blue one 
    0.25, -1.0,   0.0,  0.4,  0.4,  1.0,
    1.25, -1.0,   0.0,  1.0,  0.4,  0.4, 

    // Three triangles on the left side
   -0.75,  1.0,  -4.0,  0.4,  1.0,  0.4, // The back green one
   -1.25, -1.0,  -4.0,  0.4,  1.0,  0.4,
   -0.25, -1.0,  -4.0,  1.0,  0.4,  0.4, 

   -0.75,  1.0,  -2.0,  1.0,  1.0,  0.4, // The middle yellow one
   -1.25, -1.0,  -2.0,  1.0,  1.0,  0.4,
   -0.25, -1.0,  -2.0,  1.0,  0.4,  0.4, 

   -0.75,  1.0,   0.0,  0.4,  0.4,  1.0,  // The front blue one 
   -1.25, -1.0,   0.0,  0.4,  0.4,  1.0,
   -0.25, -1.0,   0.0,  1.0,  0.4,  0.4, 
  ]);
  var n = 18; // Three vertices per triangle * 6

  // Create a buffer object
  var vertexColorbuffer = gl.createBuffer();  
  if (!vertexColorbuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // Write the vertex coordinates and color to the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorbuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);

  var FSIZE = verticesColors.BYTES_PER_ELEMENT;

  // Assign the buffer object to a_Position and enable the assignment
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if(a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0);
  gl.enableVertexAttribArray(a_Position);

  // Assign the buffer object to a_Color and enable the assignment
  var a_Color = gl.getAttribLocation(gl.program, 'a_Color');
  if(a_Color < 0) {
    console.log('Failed to get the storage location of a_Color');
    return -1;
  }

  gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3);
  gl.enableVertexAttribArray(a_Color);

  return n;
}

到目前为止，还有一个重要的问题没有完全解释，那就是矩阵为什么可以用来定义可视空间。接下来，我们尽量避开其中复杂的数学过程，稍做一些探讨。

投影矩阵的作用

首先来看透视投影矩阵。图7.24为PerspectiveView的运行效果。可以看到，运用透视投影矩阵后，场景中的三角形有了两个变化。

首先，距离较远的三角形看上去变小了;其次，三角形被不同程度地平移以贴近中心线(即视线)，使得它们看上去在视线的左右排成了两列。实际上，如图7.25(左)所示，这些三角形的大小是完全相同的，透视投影矩阵对三角形进行了两次变换:(1)根据三角形与视点的距离，按比例对三角形进行了缩小变换 ;(2) 对三角形进行平移变换，使其贴近视线，如图7.25右所示。经过了这两次变换之后，就产生了图7.20那张照片中的深度效果。

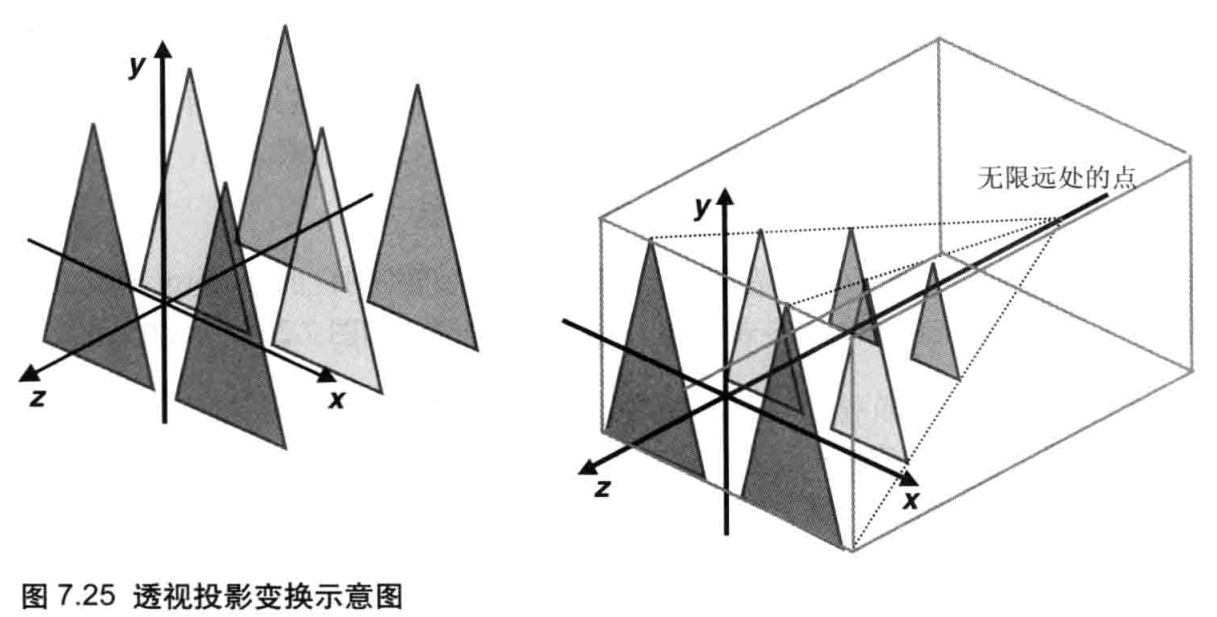
这表明，可视空间的规范(对透视投影可视空间来说，就是近、远裁剪面，垂直视角，宽高比)可以用一系列基本变换(如缩放、平移)来定义。Matrix4对象的setPerspective()方法自动地根据上述可视空间的参数计算出对应的变换矩阵。

换一个角度来看，透视投影矩阵实际上将金字塔状的可视空间变换为了盒状的可视空间,这个盒状的可视空间又称规范立方体(Canonical ViewVolume)如图7.25(右)所示。

注意，正射投影矩阵不能产生深度感。正射投影矩阵的工作仅仅是将顶点从盒状的可视空间映射到规范立方体中。顶点着色器输出的顶点都必须在规范立方体中，这样才会显示在屏幕上。

有了投影矩阵、模型矩阵和视图矩阵，我们就能够处理顶点需要经过的所有的几何变换(平移、旋转、缩放)，最终达到“具有深度感”的视觉效果。

共冶一炉（模型矩阵、视图矩阵和投影矩阵）

PerspectiveView.js的一个问题是，我们用了一天段枯燥的代码来定义所有顶点和颜色的数据。示例中只有6个三角形，我们还可以手动管理这些数据，但是如果三角形的数量进一步增加的话，那可真就是一团糟了。幸运的是，对这个问题，确实还有更高效的方法。

仔细观察图7.26，你会发现左右两组三角形的大小、位置、颜色都是对应的。如果在虚线标识处也有这样3个三角形，那么将它们向X轴正方向平移0.75单位就可以得到右侧的三角形，向X轴负方向平移0.75单位就可以得到左侧的三角形。

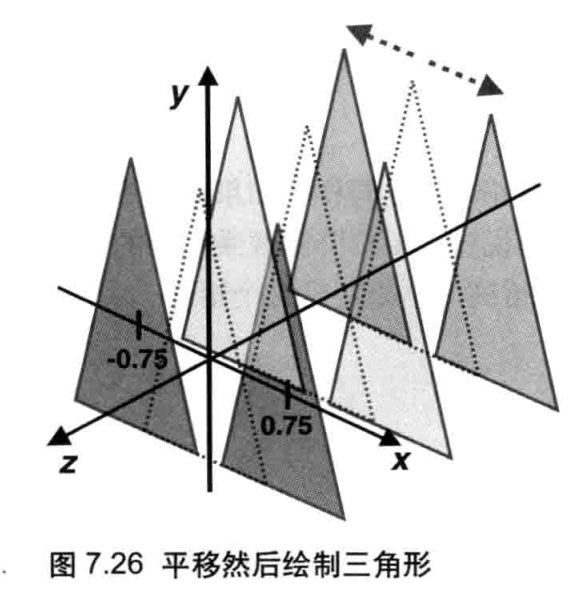
利用这一点，我们只需按照下面的步骤，就能获得PerspectiveView的效果了:

在虎线处，即沿着Z轴准备3个三角形的顶点数据。

将其沿X轴正方向(以原始位置为基准)平移0.75单位，绘制这些三角形。

将沿X轴负方向(以原始位置为基准)平移0.75单位，绘制这些三角形。

PerspectiveView程序使用投影矩阵定义可视空间，使用视图矩阵定义观察者，而PerspectiveView_mvp程序又加入了模型矩阵，用来对三角形进行变换。

之前编写的程序LookAtTriangles，该程序允许观察者从自定义的位置观察旋转后的三角形。式71描述了三角形顶点的变换过程。

<视图矩阵>x<模型矩阵>x<顶点坐标>

后来的LookAtTriangles_ViewVolume程序(该程序修复了三角形的一个角被切掉的错误)使用式73来计算最终的顶点坐标，其中投影矩阵有可能是正射投影矩阵或透视投影矩阵。

<投影矩阵>x<视图矩阵>x<顶点坐标>

可以从上述两式推断出:

上式表示，在WebGL中，你可以使用投影阵、视图矩阵、模型矩阵这3种矩阵计算出最终的顶点坐标(即顶点在规范立方体中的坐标)。

如果投影矩阵为单位阵，那么式74与式71就完全相同了;同样，如果模型矩阵为单位阵，那么式7.4与式73就完全相同了。在第4章中说过，单位阵就像乘法中的1一样，它乘以任意一个矩阵，或者任意一个矩阵乘以它，得到的结果还是这个矩阵。

// PerspectiveView_mvp.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'uniform mat4 u_ModelMatrix;\n' +
  'uniform mat4 u_ViewMatrix;\n' +
  'uniform mat4 u_ProjMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_ProjMatrix * u_ViewMatrix * u_ModelMatrix * a_Position;\n' +
  '  v_Color = a_Color;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex coordinates and color (the blue triangle is in the front)
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0, 0, 0, 1);

  // Get the storage locations of u_ModelMatrix, u_ViewMatrix, and u_ProjMatrix
  var u_ModelMatrix = gl.getUniformLocation(gl.program, 'u_ModelMatrix');
  var u_ViewMatrix = gl.getUniformLocation(gl.program, 'u_ViewMatrix');
  var u_ProjMatrix = gl.getUniformLocation(gl.program, 'u_ProjMatrix');
  if (!u_ModelMatrix || !u_ViewMatrix || !u_ProjMatrix) { 
    console.log('Failed to Get the storage locations of u_ModelMatrix, u_ViewMatrix, and/or u_ProjMatrix');
    return;
  }

  var modelMatrix = new Matrix4(); // 模型矩阵
  var viewMatrix = new Matrix4();  // 视图矩阵
  var projMatrix = new Matrix4();  // 投影矩阵

  // 计算模型矩阵，视图矩阵和投影矩阵
  modelMatrix.setTranslate(0.75, 0, 0);  // 平移0.75单位
  viewMatrix.setLookAt(0, 0, 5, 0, 0, -100, 0, 1, 0);
  projMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);
  // Pass the model, view, and projection matrix to the uniform variable respectively
  gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements);
  gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements);
  gl.uniformMatrix4fv(u_ProjMatrix, false, projMatrix.elements);

  gl.clear(gl.COLOR_BUFFER_BIT);   // Clear <canvas>

  gl.drawArrays(gl.TRIANGLES, 0, n);   // 绘制右侧的一组三角形

  // Prepare the model matrix for another pair of triangles
  modelMatrix.setTranslate(-0.75, 0, 0); // 平移-0.75单位
  // Modify only the model matrix
  gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements);

  gl.drawArrays(gl.TRIANGLES, 0, n);   // 绘制左侧的一组三角形
}

function initVertexBuffers(gl) {
  var verticesColors = new Float32Array([
    // Vertex coordinates and color
     0.0,  1.0,  -4.0,  0.4,  1.0,  0.4, // The back green one
    -0.5, -1.0,  -4.0,  0.4,  1.0,  0.4,
     0.5, -1.0,  -4.0,  1.0,  0.4,  0.4, 

     0.0,  1.0,  -2.0,  1.0,  1.0,  0.4, // The middle yellow one
    -0.5, -1.0,  -2.0,  1.0,  1.0,  0.4,
     0.5, -1.0,  -2.0,  1.0,  0.4,  0.4, 

     0.0,  1.0,   0.0,  0.4,  0.4,  1.0,  // The front blue one 
    -0.5, -1.0,   0.0,  0.4,  0.4,  1.0,
     0.5, -1.0,   0.0,  1.0,  0.4,  0.4, 
  ]);
  var n = 9;

  // Create a buffer object
  var vertexColorbuffer = gl.createBuffer();  
  if (!vertexColorbuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // Write the vertex information and enable it
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorbuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);

  var FSIZE = verticesColors.BYTES_PER_ELEMENT;

  // Assign the buffer object to a_Position and enable the assignment
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if(a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }

  gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0);
  gl.enableVertexAttribArray(a_Position);

  // Assign the buffer object to a_Color and enable the assignment
  var a_Color = gl.getAttribLocation(gl.program, 'a_Color');
  if(a_Color < 0) {
    console.log('Failed to get the storage location of a_Color');
    return -1;
  }
  gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3);
  gl.enableVertexAttribArray(a_Color);

  return n;
}

PerspectiveView_mvp直接在着色器中计算<投影矩阵>x<视图矩阵>x<模型矩阵>。这个式子其实和顶点没有关系，没必要在处理每个顶点时都算一遍。我们可以在JavaScript中将这三个矩阵相乘得到单个矩阵的结果，传给顶点着色器，就像在LookAtRotatedTriangles_mvMatrix中一样。传入的这个矩阵被称为模型视图投影矩阵(model view projection matrix)，我们将其命名为u_MvpMatrix。示例程序ProjectiveViewmvpMatrix完成了上述任务，顶点着色器变得简单了许多，如下所示:

// PerspectiveView_mvpMatrix.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'uniform mat4 u_MvpMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_MvpMatrix * a_Position;\n' +
  '  v_Color = a_Color;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex coordinates and color (the blue triangle is in the front)
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0, 0, 0, 1);

  // Get the storage location of u_MvpMatrix
  var u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
  if (!u_MvpMatrix) { 
    console.log('Failed to get the storage location of u_MvpMatrix');
    return;
  }

  var modelMatrix = new Matrix4(); // 模型矩阵
  var viewMatrix = new Matrix4();  // 视图矩阵
  var projMatrix = new Matrix4();  // 投影矩阵
  var mvpMatrix = new Matrix4();   // 模型视图投影矩阵

  // 计算模型矩阵，视图矩阵和投影矩阵
  modelMatrix.setTranslate(0.75, 0, 0);
  viewMatrix.setLookAt(0, 0, 5, 0, 0, -100, 0, 1, 0);
  projMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);
  // 计算模型视图投影矩阵
  mvpMatrix.set(projMatrix).multiply(viewMatrix).multiply(modelMatrix);
  // Pass the model view projection matrix to u_MvpMatrix
  gl.uniformMatrix4fv(u_MvpMatrix, false, mvpMatrix.elements);

  gl.clear(gl.COLOR_BUFFER_BIT);   // Clear <canvas>

  gl.drawArrays(gl.TRIANGLES, 0, n);   // Draw the triangles

　// 计算模型矩阵，视图矩阵和投影矩阵
  modelMatrix.setTranslate(-0.75, 0, 0);
  // 计算模型视图投影矩阵
  mvpMatrix.set(projMatrix).multiply(viewMatrix).multiply(modelMatrix);
  // Pass the model view projection matrix to u_MvpMatrix
  gl.uniformMatrix4fv(u_MvpMatrix, false, mvpMatrix.elements);

  gl.drawArrays(gl.TRIANGLES, 0, n);   // Draw the triangles
}

function initVertexBuffers(gl) {
  var verticesColors = new Float32Array([
    // Vertex coordinates and color
     0.0,  1.0,  -4.0,  0.4,  1.0,  0.4, // The back green one
    -0.5, -1.0,  -4.0,  0.4,  1.0,  0.4,
     0.5, -1.0,  -4.0,  1.0,  0.4,  0.4, 

     0.0,  1.0,  -2.0,  1.0,  1.0,  0.4, // The middle yellow one
    -0.5, -1.0,  -2.0,  1.0,  1.0,  0.4,
     0.5, -1.0,  -2.0,  1.0,  0.4,  0.4, 

     0.0,  1.0,   0.0,  0.4,  0.4,  1.0,  // The front blue one 
    -0.5, -1.0,   0.0,  0.4,  0.4,  1.0,
     0.5, -1.0,   0.0,  1.0,  0.4,  0.4, 
  ]);
  var n = 9;

  // Create a buffer object
  var vertexColorBuffer = gl.createBuffer();  
  if (!vertexColorBuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // Write the vertex information and enable it
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorBuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);

  var FSIZE = verticesColors.BYTES_PER_ELEMENT;

  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if(a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0);
  gl.enableVertexAttribArray(a_Position);

  var a_Color = gl.getAttribLocation(gl.program, 'a_Color');
  if(a_Color < 0) {
    console.log('Failed to get the storage location of a_Color');
    return -1;
  }
  gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3);
  gl.enableVertexAttribArray(a_Color);

  return n;
}

正确处理对象的前后关系

在真实世界中，如果你将两个盒子一前一后放在桌上，如图7.27所示，前面的盒子会挡住部分后面的盒子。

看一下示例程序PerspectiveView的效果，如图7.27所示。绿色三角形的一部分被黄色和蓝色三角形挡住了。看上去似乎是WebGL专为三维图形学设计，能够自动分析出三维对象的远近，并正确处理遮挡关系。

遗憾的是，事实没有想象得那么美好。在默认情况下，WebGL 为了加速绘图操作，是按照顶点在缓冲区中的顺序来处理它们的。前面所有的示例程序我们都是故意(不管你是否注意到)先定义远的物体，后定义近的物体，从而产生正确的效果。

比如，在PerspectiveViewmvpMatrix.js中，我们按照如下顺序定义了三角形的顶点和颜色数据，注意加粗显示的Z坐标。

WebGL按照顶点在缓冲区中的顺序(第1个是最远的绿色三角形，第2是中间的黄色三角形，第3是最近的蓝色三角形)来进行绘制。后绘制的图形将覆盖已经绘制好的图形，这样就恰好产生了近处的三角形挡住远处的三角形的效果，如图 7.13 所示。

为了验证这一点，我们将缓冲区中三角形顶点数据的顺序调整一下，把近处的蓝色三角形定义在前面，然后是中间的黄色三角形，最后是远处的绿色三角形，如下所示:

运行程序，你就会发现本该出现在最远处的绿色三角形，不自然地挡住了近处的黄色和蓝色三角形，如图7.28所示。

WebGL 在默认情况下会按照缓冲区中的顺序绘制图形，而且后绘制的图形覆盖先绘制的图形，因为这样做很高效。"如果场景中的对象不发生运动，观察者的状态也是唯一的，那么这种做法没有问题。但是如果，比如说你希望不断移动视点，从不同的角度看物体，那么你不可能事先决定对象出现的顺序。

隐藏面消除

为了解决这个问题，WebGL提供了隐藏面消除(hidden surface removal)功能。这个功能会帮助我们消除那些被遮挡的表面(隐藏面)，你可以放心地绘制场景而不必顾及各物体在缓冲区中的顺序,因为那些远处的物体会自动被近处的物体挡住,不会被绘制出来。这个功能已经内嵌在 WebGL 中了，你只需要简单地开启这个功能就可以了。

开启隐藏面消除功能，需要遵循以下两步:

开启隐藏面消除功能。
gl.enable(gl.DEPTH_TEST);

在绘制之前，清除深度缓冲区。
gl.clear(gl.DEPTH_BUFFER_BIT);

第1步所用的gl.enable()函数实际上可以开启WebGL中的多种功能，其规范如下:

第2步，使用gl.clear()方法清除深度缓冲区(depth buffer)。深度缓冲区是一个中间对象,其作用就是帮助 WebGL 进行隐藏面消除。WebGL在颜色缓冲区中绘制几何图形，绘制完成后将颜色缓冲区显示到canvas上。如果要将隐藏面消除，那就必须知道每个几何图形的深度信息，而深度缓冲区就是用来存储深度信息的。由于深度方向通常是Z轴方向，所以有时候我们也称它为Z缓冲区。

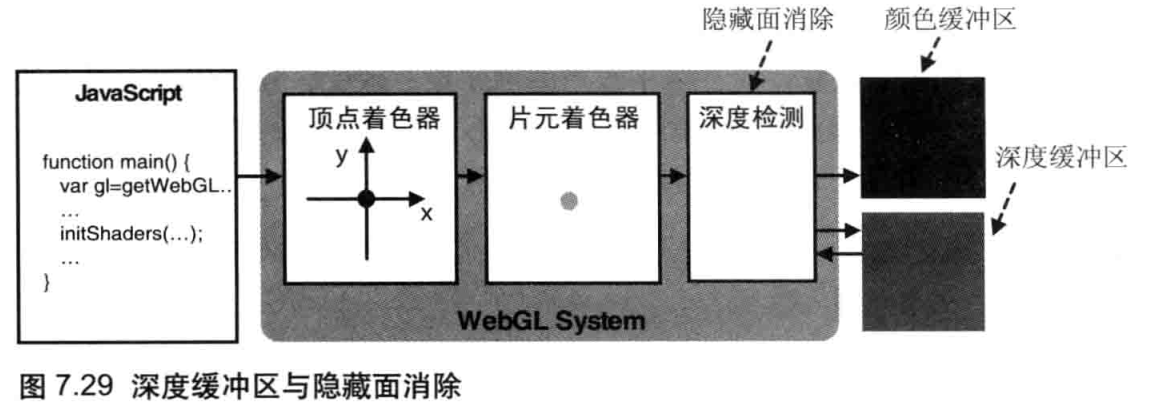
在绘制任意一帧之前，都必须清除深度缓冲区，以消除绘制上一帧时在其中留下的痕迹。如果不这样做，就会出现错误的结果。我们调用gl.clear()函数，并传入参数gl.DEPTH BUFFER BIT清除深度缓冲区:

gl.clear(gl.DEPTH_BUFFER_BIT);

当然，还需要清除颜色缓冲区。用按位或符号(I)连接 gl.DEPTH_BUFFER_BIT 和 gl.COLOR_BUFFER_BIT，并作为参数传人glclear()中:

gl.clear(gl.COLOR_BUFFER_BIT| gl.DEPTH_BUFFER_BIT);

类似地，同时清除任意两个缓冲区时，都可以使用按位或符号。

与gl.enable()函数对应的还有gl.disable()函数，其规范如下所示，前者启用某个功能，后者则禁用之。

示例程序名为DepthBuffer.js，它在PerspectiveView_mvpMatrixjs的基础上，加入了隐藏面消除的相关代码。注意，缓冲区中顶点的顺序没有改变，程序依然按照近处(蓝色)，中间(黄色)，远处(绿色)的顺序绘制三角形。程序运行的效果和Perspec-tiveView_mvpMatrix完全一样，程序的代码如例7.10所示。

// DepthBuffer.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'uniform mat4 u_mvpMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_mvpMatrix * a_Position;\n' +
  '  v_Color = a_Color;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex coordinates and color (the blue triangle is in the front)
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Specify the color for clearing <canvas>
  gl.clearColor(0.0, 0.0, 0.0, 1.0);
  // 开启隐藏面消除
  gl.enable(gl.DEPTH_TEST);

  // Get the storage location of u_mvpMatrix
  var u_mvpMatrix = gl.getUniformLocation(gl.program, 'u_mvpMatrix');
  if (!u_mvpMatrix) { 
    console.log('Failed to get the storage location of u_mvpMatrix');
    return;
  }

  var modelMatrix = new Matrix4(); // Model matrix
  var viewMatrix = new Matrix4();  // View matrix
  var projMatrix = new Matrix4();  // Projection matrix
  var mvpMatrix = new Matrix4();   // Model view projection matrix

  // Calculate the view matrix and the projection matrix
  modelMatrix.setTranslate(0.75, 0, 0);
  viewMatrix.setLookAt(0, 0, 5, 0, 0, -100, 0, 1, 0);
  projMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);
  // Calculate the model view projection matrix
  mvpMatrix.set(projMatrix).multiply(viewMatrix).multiply(modelMatrix);
  // Pass the model view projection matrix
  gl.uniformMatrix4fv(u_mvpMatrix, false, mvpMatrix.elements);

  // 清空颜色和深度缓冲区
  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

  gl.drawArrays(gl.TRIANGLES, 0, n);   // Draw the triangles

  // Prepare the model matrix for another pair of triangles
  modelMatrix.setTranslate(-0.75, 0, 0);
  // Calculate the model view projection matrix
  mvpMatrix.set(projMatrix).multiply(viewMatrix).multiply(modelMatrix);
  // Pass the model view projection matrix to u_MvpMatrix
  gl.uniformMatrix4fv(u_mvpMatrix, false, mvpMatrix.elements);

  gl.drawArrays(gl.TRIANGLES, 0, n);   // Draw the triangles
}

function initVertexBuffers(gl) {
  var verticesColors = new Float32Array([
    // Vertex coordinates and color
     0.0,  1.0,   0.0,  0.4,  0.4,  1.0,  // 前面的蓝色三角形 
    -0.5, -1.0,   0.0,  0.4,  0.4,  1.0,
     0.5, -1.0,   0.0,  1.0,  0.4,  0.4, 

     0.0,  1.0,  -2.0,  1.0,  1.0,  0.4, // 中间的黄色三角形
    -0.5, -1.0,  -2.0,  1.0,  1.0,  0.4,
     0.5, -1.0,  -2.0,  1.0,  0.4,  0.4,

     0.0,  1.0,  -4.0,  0.4,  1.0,  0.4, // 后面的绿色三角形
    -0.5, -1.0,  -4.0,  0.4,  1.0,  0.4,
     0.5, -1.0,  -4.0,  1.0,  0.4,  0.4, 
  ]);
  var n = 9;

  // Create a buffer object
  var vertexColorbuffer = gl.createBuffer();  
  if (!vertexColorbuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // Write vertex information to buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorbuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);

  var FSIZE = verticesColors.BYTES_PER_ELEMENT;
  // Assign the buffer object to a_Position and enable the assignment
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if(a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0);
  gl.enableVertexAttribArray(a_Position);
  // Assign the buffer object to a_Color and enable the assignment
  var a_Color = gl.getAttribLocation(gl.program, 'a_Color');
  if(a_Color < 0) {
    console.log('Failed to get the storage location of a_Color');
    return -1;
  }
  gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3);
  gl.enableVertexAttribArray(a_Color);

  // Unbind the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, null);

  return n;
}

运行程序，可见程序成功地消除了隐藏面，位于近处的三角形挡住了远处的三角形。该程序证明了不管视点位于何处，隐藏面都能够被消除。在任何三维场景中，你都应该开启隐藏面消除，并在适当的时刻清空深度缓冲区(通常是在绘制每一帧前)。

应当注意的是,隐藏面消除的前提是正确设置可视空间,否则就可能产生错误的结果。不管是盒状的正射投影空间，还是金字塔状的透视投影空间，你必须使用一个。

深度冲突

隐藏面消除是WebGL的一项复杂而又强大的特性，在绝大多数情况下，它都能很好地完成任务。然而，当几何图形或物体的两个表面极为接近时，就会出现新的问题，使得表面看上去斑斑驳驳的，如图7.30所示。这种现象被称为深度冲突(Zfighting)。现在，我们来画两个Z值完全一样的三角形。

之所以会产生深度冲突，是因为两个表面过于接近，深度缓冲区有限的精度已经不能区分哪个在前，哪个在后了。严格地说，如果创建三维模型阶段就对顶点的深度值加以注意，是能够避免深度冲突的。但是，当场景中有多个运动着的物体时，实现这一点
几乎是不可能的。

WebGL提供一种被称为多边形偏移(polygon offset)的机制来解决这个问题。该机制将自动在Z值加上一个偏移量，偏移量的值由物体表面相对于观察者视线的角度来确定。启用该机制只需要两行代码:

启用多边形偏移。
gl.enable(g1.POLYGON OFFSET FILL);

在绘制之前指定用来计算偏移量的参数。
g1.polygonOffset(10，1.0);

第1步调用了gl.enable()启用多边形偏移，注意启用隐藏面消除用到的也是该函数，只不过两者传入了不同的参数。第2步中的函数gl.polygonOffset()的规范如下。

// Zfighting.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'uniform mat4 u_ViewProjMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_ViewProjMatrix * a_Position;\n' +
  '  v_Color = a_Color;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex coordinates and color (the blue triangle is in the front)
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  //Set clear color and enable the hidden surface removal function
  gl.clearColor(0, 0, 0, 1);
  gl.enable(gl.DEPTH_TEST);

  // Get the storage locations of u_ViewProjMatrix
  var u_ViewProjMatrix = gl.getUniformLocation(gl.program, 'u_ViewProjMatrix');
  if (!u_ViewProjMatrix) { 
    console.log('Failed to get the storage locations of u_ViewProjMatrix');
    return;
  }

  var viewProjMatrix = new Matrix4();
  // Set the eye point, look-at point, and up vector.
  viewProjMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);
  viewProjMatrix.lookAt(3.06, 2.5, 10.0, 0, 0, -2, 0, 1, 0);

  // Pass the view projection matrix to u_ViewProjMatrix
  gl.uniformMatrix4fv(u_ViewProjMatrix, false, viewProjMatrix.elements);

  // Clear color and depth buffer
  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

  // 启用多边形偏移
  gl.enable(gl.POLYGON_OFFSET_FILL);
  // Draw the triangles
  gl.drawArrays(gl.TRIANGLES, 0, n/2);   // The green triangle
    gl.polygonOffset(1.0, 1.0);          // 设置多边形偏移
  gl.drawArrays(gl.TRIANGLES, n/2, n/2); // The yellow triangle
}

function initVertexBuffers(gl) {
  var verticesColors = new Float32Array([
    // Vertex coordinates and color
     0.0,  2.5,  -5.0,  0.4,  1.0,  0.4, // 绿色三角形
    -2.5, -2.5,  -5.0,  0.4,  1.0,  0.4,
     2.5, -2.5,  -5.0,  1.0,  0.4,  0.4, 

     0.0,  3.0,  -5.0,  1.0,  0.4,  0.4, // 黄色三角形
    -3.0, -3.0,  -5.0,  1.0,  1.0,  0.4,
     3.0, -3.0,  -5.0,  1.0,  1.0,  0.4, 
  ]);
  var n = 6;

  // Create a buffer object
  var vertexColorbuffer = gl.createBuffer();  
  if (!vertexColorbuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }

  // Write the vertex coordinates and color to the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorbuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);

  var FSIZE = verticesColors.BYTES_PER_ELEMENT;
  // Assign the buffer object to a_Position and enable the assignment
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if(a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0);
  gl.enableVertexAttribArray(a_Position);
  // Assign the buffer object to a_Color and enable the assignment
  var a_Color = gl.getAttribLocation(gl.program, 'a_Color');
  if(a_Color < 0) {
    console.log('Failed to get the storage location of a_Color');
    return -1;
  }
  gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3);
  gl.enableVertexAttribArray(a_Color);

  return n;
}

可见,所有顶点的Z坐标值都一样,为-0.5，但是却没有出现深度冲突现象。

在代码的其余部分，我们开启了多边形偏移机制，然后绘制了一个绿色的三角形和一个黄色的三角形。两个三角形的数据存储在同一个缓冲区中，所以需要格外注意gl.drawArrays()的第2个和第3个参数。第2个参数表示开始绘制的顶点的编号，而第3个参数表示该次操作绘制的顶点个数。所以，我们先画了一个绿色三角形，然后通过 g1.polygonOffset()设置了多边形偏移参数，使之后的绘制受到多边形偏移机制影响，再画了一个黄色三角形。运行程序，你将看到两个三角形没有发生深度冲突。

立方体

迄今为止，本书通过绘制一些简单的三角形，向你展示了 WebGL 的诸多特性。你对绘制三维对象的基础知识应该已经有了足够的了解。下面，我们就来绘制如图 7.31 所示的立方体 (图右侧显示了立方体每个顶点的坐标)，其 8 个顶点的颜色分别为白色、品红色 (亮紫色)、红色、黄色、绿色、青色 (蓝绿色)、蓝色、黑色。第5章中曾提到过,为每个顶点定义颜色后，表面上的颜色会根据顶点颜色内插出来，形成一种光滑的渐变效果 (“色体”，相当于二维的“色轮”)。新的程序名为 HelloCube。

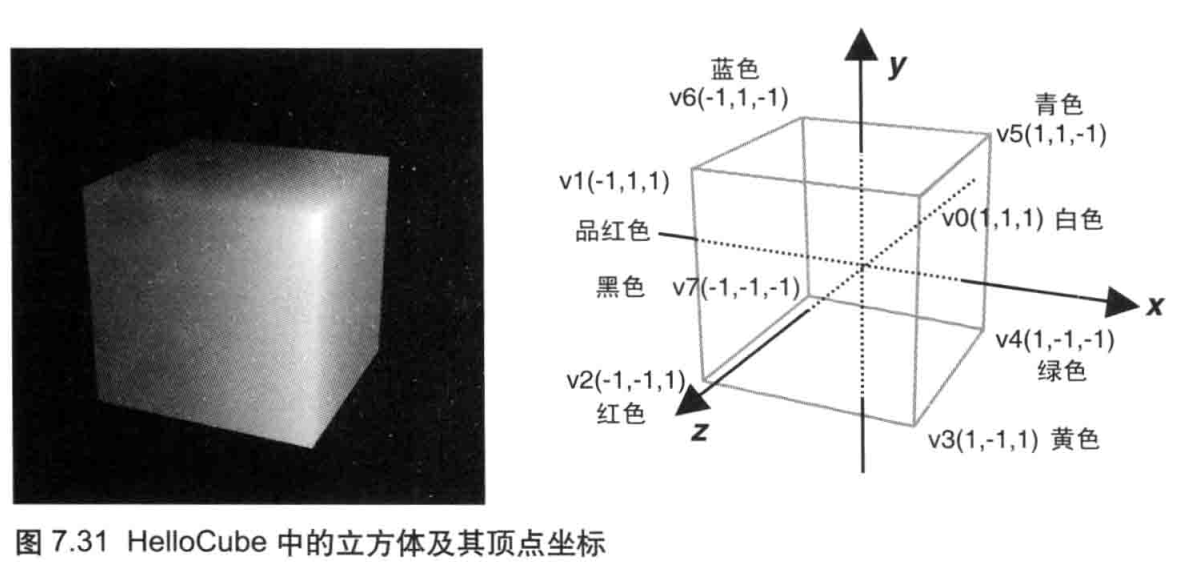
目前，我们都是调用 gl.drawArrays) 方法来进行绘制操作的。考虑一下，如何用该函数绘制出一个立方体呢。我们只能使用 gl.TRIANGLES、GL.TRIANGLE STRIP 或者gL.TRIANGLE_FAN 模式来绘制三角形，那么最简单也最直接的方法就是，通过绘制两个三角形来拼成立方体的一个矩形表面。换句话说，为了绘制四个顶点 (v0,vl,v2,v3) 组成的矩形表面，你可以分别绘制三角形(v0,vl,v2) 和三角形(v0,v2,v3)。对立方体的所有表面都这样做就绘制出了整个立方体。

立方体的每一个面由两个三角形组成，每个三角形有3 个顶点，所以每个面需要用到6个顶点。立方体共有6 个面，一共需要 6x6-36 个顶点。将 36 个顶点的数据写人缓冲区，再调用 gl.drawArrays(gl.TRIANGLES，0，36) 就可以绘制出立方体。问题是，立方体实际只有 8 个顶点，而我们却定义了36 个之多，这是因为每个顶点都会被多个三角形共用。

或者,你也可以使用 gI.TRIANGLE EAN模式来绘制立方体。在gl.TRIANGLE EAN模式下用4个顶点 (vo,vl,v2,v3)就可以绘制出一个四边形,所以你只需要 4x6-24 个顶点“。但是，如果这样做你就必须为立方体的每个面调用一次 gl.drawArrays()，一共需要6 次调用。所以，两种绘制模式各有优缺点，没有一种是完美的。

如你所愿，WebGL 确实提供了一种完美的方案:gl.drawElements0)。使用该函数替代 gl.drawArrays() 函数进行绘制，能够避免重复定义顶点，保持顶点数量最小。为此你需要知道模型的每一个顶点的坐标，这些顶点坐标描述了整个模型 (立方体)。

我们将立方体拆成顶点和三角形，如图 7.32(左)所示。立方体被拆成6 个面:前后、左、右、上、下，每个面都由两个三角形组成，与三角形列表中的两个三角形相关联。每个三角形都有3 个顶点，与顶点列表中的3 个顶点相关联，如图 7.32 (右)所示三角形列表中的数字表示该三角形的3 个顶点在顶点列表中的索引值。顶点列表中共有8 个顶点，索引值为从 0到 7。

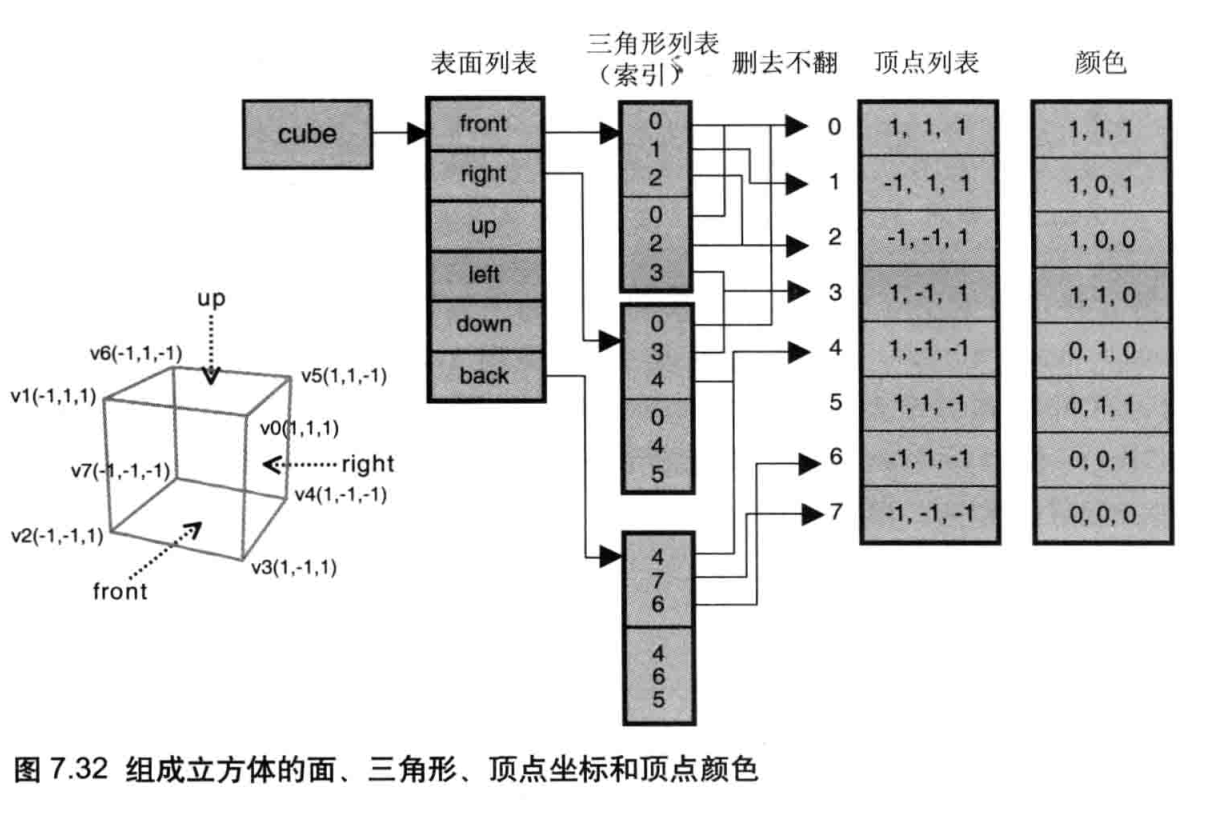
这样用一个数据结构就可以描述出立方体是怎样由顶点坐标和颜色构成的了。

通过顶点索引绘制物体

到目前为止，我们都是使用 gl.drawArrays() 进行绘制，现在我们要使用另一个方法 gl.drawElements()。首先，我们来看一下如何使用 gl.drawElements()。我们需要在 gl.ELEMENT_ARRAY_BUEEER (而不是之前一直使用的 gl.ARRAY_BUEEER，见第 4章)中指定顶点的索引值。所以两种方法最重要的区别就在于gl.ELEMENT_ARRAY_BUFFER，它管理着具有索引结构的三维模型数据。

我们需要将顶点索引 (也就是三角形列表中的内容) 写人到缓冲区中，并绑定到 gl.ELEMENT_ARRAY_BUFEER 上，其过程类似于调用 gl.drawArrays() 时将顶点坐标写人缓冲区并将其绑定到 gl.ARRAY _BUFFER 上的过程。也就是说，可以继续使用gl.bindBuffer()和 gl.bufferData() 来进行上述操作，只不过参数 target 要改为G1.ELEMENT ARRAY BUFFER。来看一下示例程序。

// HelloCube.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'uniform mat4 u_MvpMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_MvpMatrix * a_Position;\n' +
  '  v_Color = a_Color;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex coordinates and color
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // 设置背景色并开启隐藏面消除
  gl.clearColor(0.0, 0.0, 0.0, 1.0);
  gl.enable(gl.DEPTH_TEST);

  // Get the storage location of u_MvpMatrix
  var u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
  if (!u_MvpMatrix) { 
    console.log('Failed to get the storage location of u_MvpMatrix');
    return;
  }

  // Set the eye point and the viewing volume
  var mvpMatrix = new Matrix4();
  mvpMatrix.setPerspective(30, 1, 1, 100);
  mvpMatrix.lookAt(3, 3, 7, 0, 0, 0, 0, 1, 0);

  // Pass the model view projection matrix to u_MvpMatrix
  gl.uniformMatrix4fv(u_MvpMatrix, false, mvpMatrix.elements);

  // 清理颜色缓冲区和深度缓冲区
  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

  // 绘制立方体
  gl.drawElements(gl.TRIANGLES, n, gl.UNSIGNED_BYTE, 0);
}

function initVertexBuffers(gl) {
  // Create a cube
  //    v6----- v5
  //   /|      /|
  //  v1------v0|
  //  | |     | |
  //  | |v7---|-|v4
  //  |/      |/
  //  v2------v3
  var verticesColors = new Float32Array([
    // 顶点坐标和颜色
     1.0,  1.0,  1.0,     1.0,  1.0,  1.0,  // v0 White
    -1.0,  1.0,  1.0,     1.0,  0.0,  1.0,  // v1 Magenta
    -1.0, -1.0,  1.0,     1.0,  0.0,  0.0,  // v2 Red
     1.0, -1.0,  1.0,     1.0,  1.0,  0.0,  // v3 Yellow
     1.0, -1.0, -1.0,     0.0,  1.0,  0.0,  // v4 Green
     1.0,  1.0, -1.0,     0.0,  1.0,  1.0,  // v5 Cyan
    -1.0,  1.0, -1.0,     0.0,  0.0,  1.0,  // v6 Blue
    -1.0, -1.0, -1.0,     0.0,  0.0,  0.0   // v7 Black
  ]);

  // 顶点索引
  var indices = new Uint8Array([
    0, 1, 2,   0, 2, 3,    // front
    0, 3, 4,   0, 4, 5,    // right
    0, 5, 6,   0, 6, 1,    // up
    1, 6, 7,   1, 7, 2,    // left
    7, 4, 3,   7, 3, 2,    // down
    4, 7, 6,   4, 6, 5     // back
 ]);

  // 创建缓冲区对象
  var vertexColorBuffer = gl.createBuffer();
  var indexBuffer = gl.createBuffer();
  if (!vertexColorBuffer || !indexBuffer) {
    return -1;
  }

  // 将顶点坐标和颜色写入缓冲区对象
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorBuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);

  var FSIZE = verticesColors.BYTES_PER_ELEMENT;
  // 将缓冲区内顶点坐标数据分配给 a_Position并开启之
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if(a_Position < 0) {
    console.log('Failed to get the storage location of a_Position');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0);
  gl.enableVertexAttribArray(a_Position);
  // 将缓冲区内颜色数据分配给 a_Position并开启之
  var a_Color = gl.getAttribLocation(gl.program, 'a_Color');
  if(a_Color < 0) {
    console.log('Failed to get the storage location of a_Color');
    return -1;
  }
  gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3);
  gl.enableVertexAttribArray(a_Color);

  // 将顶点索引数据写入缓存区对象
  gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer);
  gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW);

  return indices.length;
}

向缓冲区中写入顶点的坐标、颜色与索引

本例的 initVertexBuffers()函数通过缓冲区对象 verticesColors 向顶点着色器中的 attribute 变量传顶点坐标和颜色信息，这一点与之前无异。但是，本例不再按照verticesColors 中的顶点顺序来进行绘制，所以必须额外注意每个顶点的索引值，我们要通过索引值来指定绘制的顺序。比如说，第1个顶点的索引为 0，第2 个顶点的索引为1，等等。下面是 initvertexBuffers() 函数的部分代码 :

 // Create a cube
  //    v6----- v5
  //   /|      /|
  //  v1------v0|
  //  | |     | |
  //  | |v7---|-|v4
  //  |/      |/
  //  v2------v3
  var verticesColors = new Float32Array([
    // 顶点坐标和颜色
     1.0,  1.0,  1.0,     1.0,  1.0,  1.0,  // v0 White
    -1.0,  1.0,  1.0,     1.0,  0.0,  1.0,  // v1 Magenta
    -1.0, -1.0,  1.0,     1.0,  0.0,  0.0,  // v2 Red
     1.0, -1.0,  1.0,     1.0,  1.0,  0.0,  // v3 Yellow
     1.0, -1.0, -1.0,     0.0,  1.0,  0.0,  // v4 Green
     1.0,  1.0, -1.0,     0.0,  1.0,  1.0,  // v5 Cyan
    -1.0,  1.0, -1.0,     0.0,  0.0,  1.0,  // v6 Blue
    -1.0, -1.0, -1.0,     0.0,  0.0,  0.0   // v7 Black
  ]);

  // 顶点索引
  var indices = new Uint8Array([
    0, 1, 2,   0, 2, 3,    // front
    0, 3, 4,   0, 4, 5,    // right
    0, 5, 6,   0, 6, 1,    // up
    1, 6, 7,   1, 7, 2,    // left
    7, 4, 3,   7, 3, 2,    // down
    4, 7, 6,   4, 6, 5     // back
 ]);

	// ...
  // 创建缓存区对象
  var vertexColorBuffer = gl.createBuffer();
  var indexBuffer = gl.createBuffer();

	// ...
  // 将顶点索引数据写入缓存区对象
  gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer);
  gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW);

  return indices.length;

也许你会注意到，缓冲区对象 indexBuffer 中的数据来自于数组indices ，该数组以索引值的形式存储了绘制顶点的顺序。索引值是整型数,所以数组的类型是 uint8array(无符号 8 位整型数)。如果有超过 256 个顶点，那么就应该使用 Uint16Array。indices 中的元素如图 7.33 中的三角形列表所示，每3 个索引值1 组，指向 3 个顶点，由这3 个顶点组成 1个三角形。通常我们不需要手动创建这些顶点和索引数据，因为三维建模工具 (将第 10 章介绍)会帮助我们创建它们。

绑定缓冲区，以及向缓冲区写人索引数据的过程与之前示例程序中的很类似，区别就是绑定的目标由 gl.ARRAY_BUFEER 变成了 gL.ELEMENT_ARRAY_BUEEER。这个参数告诉 WebGL，该缓冲区中的内容是顶点的索引值数据。

此时，WebGL 系统的内部状态如图 7.34 所示

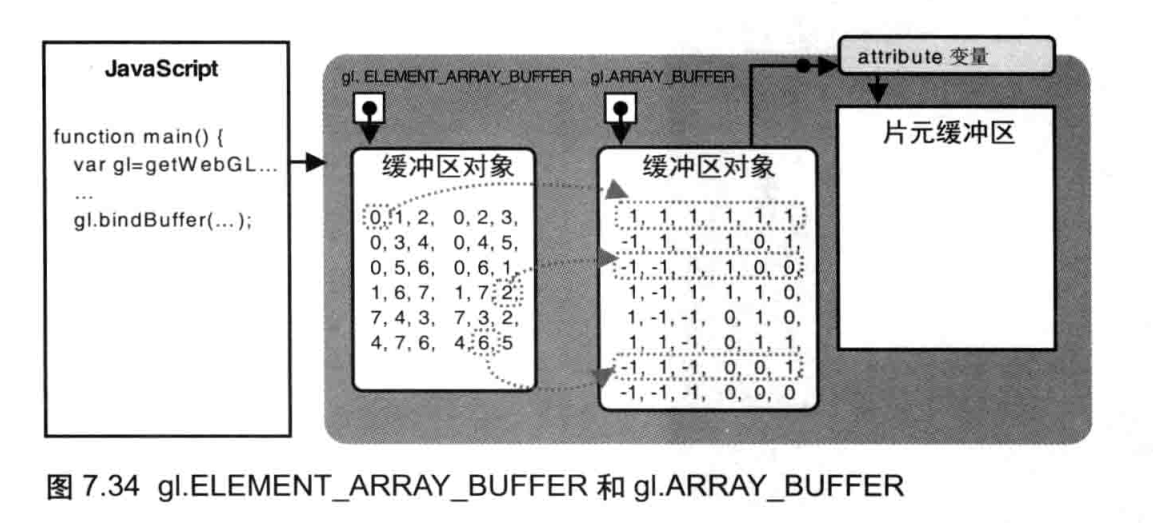
gl.drawElements()方法的第 2 个参数 n 表示顶点索引数组的长度，也就是顶点着色器的执行次数。注意，n 与 gl.ARRAY BUEEER 中的顶点个数不同。

在调用 gl.drawElements() 时，WebGL 首先从绑定到 gl.ELEMENT ARRAY_BUFFER 的缓冲区(也就是 indexBuffer)中获取顶点的索引值，然后根据该索引值，从绑定到gl.ARRAY_BUEFER 的缓冲区(即 vertexColorBuffer)中获取顶点的坐标、颜色等信息然后传递给 attribute 变量并执行顶点着色器。对每个索引值都这样做，最后就绘制出了整个立方体，而此时你只调用了一次 gl.drawElements()这种方式通过索引来访问顶点数据，从而循环利用顶点信息，控制内存的开销，但代价是你需要通过索引来间接地访问顶点，在某种程度上使程序复杂化了。所以，gl.drawElements()和 gl.drawArrays()各有优劣，具体用哪一个取决于具体的系统需求。

虽然我们已经证明了 gl.drawElements() 是高效的绘制三维图形的方式，但还是漏了关键的一点:我们无法通过将颜色定义在索引值上,颜色仍然是依赖于顶点的,如图 7.31所示。

考虑这样的情况 :我们希望立方体的每个表面都是不同的单一颜色 (而非颜色渐变效果)或者纹理图像，如图 7.35 所示。我们需要把每个面的颜色或纹理信息写入三角形列表、索引和顶点数据中，如图 7.33 所示。

我们将研究如何解决这个问题，以及如何为每个面指定颜色。

为立方体的每个表面指定颜色

顶点着色器进行的是逐顶点的计算，接收的是逐顶点的信息。这说明我们知道，如果你想指定表面的颜色，你也需要将颜色定义为逐顶点的信息，并传给顶点着色器举个例子，你想把立方体的前表面涂成蓝色，前表面由顶点v0、v1、v2、v3 组成，那么你就需要将这 4 个顶点都指定为蓝色。

但是你会发现，顶点v0 不仅在前表面上，也在右表面和上表面上，如果你将 v0 指定为蓝色，那么它在另外两个表面上也会是蓝色，这不是我们想要的结果。为了解决这个问题，我们需要创建多个具有相同顶点坐标的顶点 (虽然这样会造成一些冗余)，如图7.36 所示。如果这样做，你就必须把那些具有相同坐标的顶点分开处理。

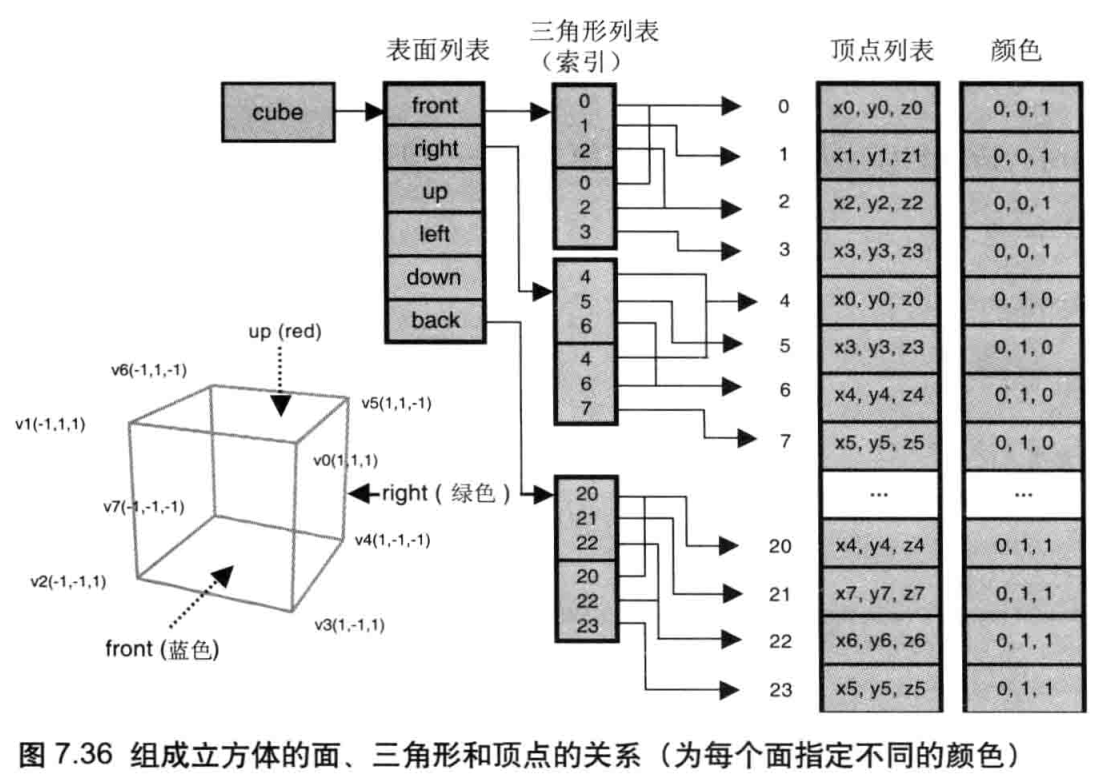
此时的三角形列表，也就是顶点索引值序列，对每个面都指向一组不同的顶点，不再有前表面和上表面共享一个顶点的情况。这样一来，就可以实现前述的效果，为每个表面涂上不同的单色了。我们也可以使用类似的方法为立方体的每个表面贴上不同的纹理，只需要将图 7.36 中的颜色值换成纹理坐标即可。

现在来看一下示例程序 ColoredCube 的代码，它绘制出了一个立方体，其每个表面涂上了不同的颜色。程序的效果如图 7.35 所示。

// ColoredCube.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'uniform mat4 u_MvpMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_MvpMatrix * a_Position;\n' +
  '  v_Color = a_Color;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex information
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Set the clear color and enable the depth test
  gl.clearColor(0.0, 0.0, 0.0, 1.0);
  gl.enable(gl.DEPTH_TEST);

  // Get the storage location of u_MvpMatrix
  var u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
  if (!u_MvpMatrix) {
    console.log('Failed to get the storage location of u_MvpMatrix');
    return;
  }

  // Set the eye point and the viewing volume
  var mvpMatrix = new Matrix4();
  mvpMatrix.setPerspective(30, 1, 1, 100);
  mvpMatrix.lookAt(3, 3, 7, 0, 0, 0, 0, 1, 0);

  // Pass the model view projection matrix to u_MvpMatrix
  gl.uniformMatrix4fv(u_MvpMatrix, false, mvpMatrix.elements);

  // Clear color and depth buffer
  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

  // Draw the cube
  gl.drawElements(gl.TRIANGLES, n, gl.UNSIGNED_BYTE, 0);
}

function initVertexBuffers(gl) {
  // Create a cube
  //    v6----- v5
  //   /|      /|
  //  v1------v0|
  //  | |     | |
  //  | |v7---|-|v4
  //  |/      |/
  //  v2------v3

  var vertices = new Float32Array([   // 顶点坐标
     1.0, 1.0, 1.0,  -1.0, 1.0, 1.0,  -1.0,-1.0, 1.0,   1.0,-1.0, 1.0,  // v0-v1-v2-v3 front
     1.0, 1.0, 1.0,   1.0,-1.0, 1.0,   1.0,-1.0,-1.0,   1.0, 1.0,-1.0,  // v0-v3-v4-v5 right
     1.0, 1.0, 1.0,   1.0, 1.0,-1.0,  -1.0, 1.0,-1.0,  -1.0, 1.0, 1.0,  // v0-v5-v6-v1 up
    -1.0, 1.0, 1.0,  -1.0, 1.0,-1.0,  -1.0,-1.0,-1.0,  -1.0,-1.0, 1.0,  // v1-v6-v7-v2 left
    -1.0,-1.0,-1.0,   1.0,-1.0,-1.0,   1.0,-1.0, 1.0,  -1.0,-1.0, 1.0,  // v7-v4-v3-v2 down
     1.0,-1.0,-1.0,  -1.0,-1.0,-1.0,  -1.0, 1.0,-1.0,   1.0, 1.0,-1.0   // v4-v7-v6-v5 back
  ]);

  var colors = new Float32Array([     // 颜色
    0.4, 0.4, 1.0,  0.4, 0.4, 1.0,  0.4, 0.4, 1.0,  0.4, 0.4, 1.0,  // v0-v1-v2-v3 front(blue)
    0.4, 1.0, 0.4,  0.4, 1.0, 0.4,  0.4, 1.0, 0.4,  0.4, 1.0, 0.4,  // v0-v3-v4-v5 right(green)
    1.0, 0.4, 0.4,  1.0, 0.4, 0.4,  1.0, 0.4, 0.4,  1.0, 0.4, 0.4,  // v0-v5-v6-v1 up(red)
    1.0, 1.0, 0.4,  1.0, 1.0, 0.4,  1.0, 1.0, 0.4,  1.0, 1.0, 0.4,  // v1-v6-v7-v2 left
    1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  // v7-v4-v3-v2 down
    0.4, 1.0, 1.0,  0.4, 1.0, 1.0,  0.4, 1.0, 1.0,  0.4, 1.0, 1.0   // v4-v7-v6-v5 back
  ]);

  var indices = new Uint8Array([       // 顶点索引
     0, 1, 2,   0, 2, 3,    // front
     4, 5, 6,   4, 6, 7,    // right
     8, 9,10,   8,10,11,    // up
    12,13,14,  12,14,15,    // left
    16,17,18,  16,18,19,    // down
    20,21,22,  20,22,23     // back
  ]);

  // 创建缓存区对象
  var indexBuffer = gl.createBuffer();
  if (!indexBuffer) 
    return -1;

  // 将顶点坐标和颜色写入缓存区对象
  if (!initArrayBuffer(gl, vertices, 3, gl.FLOAT, 'a_Position'))
    return -1;

  if (!initArrayBuffer(gl, colors, 3, gl.FLOAT, 'a_Color'))
    return -1;

  // 将顶点索引写入缓存区对象
  gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer);
  gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW);

  return indices.length;
}

function initArrayBuffer(gl, data, num, type, attribute) {
  var buffer = gl.createBuffer();   // 创建缓存区对象
  if (!buffer) {
    console.log('Failed to create the buffer object');
    return false;
  }
  // Write date into the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
  gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);
  // Assign the buffer object to the attribute variable
  var a_attribute = gl.getAttribLocation(gl.program, attribute);
  if (a_attribute < 0) {
    console.log('Failed to get the storage location of ' + attribute);
    return false;
  }
  gl.vertexAttribPointer(a_attribute, num, type, false, 0, 0);
  // Enable the assignment of the buffer object to the attribute variable
  gl.enableVertexAttribArray(a_attribute);

  return true;
}

如果将所有面颜色设置为相同颜色，比如白色（coloreCube_singleColor.js）；立方体各表面颜色相同的后果就是，我们很难辨认出这是个立方体，还是什么其他东西。我们之前能够辩认出立方体，那是因为它的每个面都是不同的颜色，而现在，我们只能看到一个白色的不规则六边形。总之，如果物体各表面颜色相同，它就会失去立体感。

相反，在现实世界中，一个纯白色的立方体被放在桌上的时候，你仍然还是能够辩认出它的。实际上，现实中的立方体各个表面虽然是同一个颜色，但是看上去却有轻微的差异，因为各个表面的角度不同，受到环境中光照的情况也不同，而这些都没有在程序中实现。下一章将研究如何实现三维场景中的光照。

// ColoredCube_singleColor.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'uniform mat4 u_MvpMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_MvpMatrix * a_Position;\n' +
  '  v_Color = a_Color;\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex information
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Set the clear color and enable the depth test
  gl.clearColor(0.0, 0.0, 0.0, 1.0);
  gl.enable(gl.DEPTH_TEST);

  // Get the storage location of u_MvpMatrix
  var u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
  if (!u_MvpMatrix) {
    console.log('Failed to get the storage location of u_MvpMatrix');
    return;
  }

  // Set the eye point and the viewing volume
  var mvpMatrix = new Matrix4();
  mvpMatrix.setPerspective(30, 1, 1, 100);
  mvpMatrix.lookAt(3, 3, 7, 0, 0, 0, 0, 1, 0);

  // Pass the model view projection matrix to u_MvpMatrix
  gl.uniformMatrix4fv(u_MvpMatrix, false, mvpMatrix.elements);

  // Clear color and depth buffer
  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

  // Draw the cube
  gl.drawElements(gl.TRIANGLES, n, gl.UNSIGNED_BYTE, 0);
}

function initVertexBuffers(gl) {
  // Create a cube
  //    v6----- v5
  //   /|      /|
  //  v1------v0|
  //  | |     | |
  //  | |v7---|-|v4
  //  |/      |/
  //  v2------v3

  var vertices = new Float32Array([   // Vertex coordinates
     1.0, 1.0, 1.0,  -1.0, 1.0, 1.0,  -1.0,-1.0, 1.0,   1.0,-1.0, 1.0,    // v0-v1-v2-v3 front
     1.0, 1.0, 1.0,   1.0,-1.0, 1.0,   1.0,-1.0,-1.0,   1.0, 1.0,-1.0,    // v0-v3-v4-v5 right
     1.0, 1.0, 1.0,   1.0, 1.0,-1.0,  -1.0, 1.0,-1.0,  -1.0, 1.0, 1.0,    // v0-v5-v6-v1 up
    -1.0, 1.0, 1.0,  -1.0, 1.0,-1.0,  -1.0,-1.0,-1.0,  -1.0,-1.0, 1.0,    // v1-v6-v7-v2 left
    -1.0,-1.0,-1.0,   1.0,-1.0,-1.0,   1.0,-1.0, 1.0,  -1.0,-1.0, 1.0,    // v7-v4-v3-v2 down
     1.0,-1.0,-1.0,  -1.0,-1.0,-1.0,  -1.0, 1.0,-1.0,   1.0, 1.0,-1.0     // v4-v7-v6-v5 back
  ]);

  var colors = new Float32Array([     // 所有矩形面颜色为白色
    1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  // v0-v1-v2-v3 front(white)
    1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  // v0-v3-v4-v5 right(white)
    1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  // v0-v5-v6-v1 up(white)
    1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  // v1-v6-v7-v2 left(white)
    1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  // v7-v4-v3-v2 down(white)
    1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  1.0, 1.0, 1.0,  1.0, 1.0, 1.0   // v4-v7-v6-v5 back(white)
  ]);

  var indices = new Uint8Array([       // Indices of the vertices
     0, 1, 2,   0, 2, 3,    // front
     4, 5, 6,   4, 6, 7,    // right
     8, 9,10,   8,10,11,    // up
    12,13,14,  12,14,15,    // left
    16,17,18,  16,18,19,    // down
    20,21,22,  20,22,23     // back
  ]);

  // Create a buffer object
  var indexBuffer = gl.createBuffer();
  if (!indexBuffer) 
    return -1;

  // Write the vertex coordinates and color to the buffer object
  if (!initArrayBuffer(gl, vertices, 3, gl.FLOAT, 'a_Position'))
    return -1;

  if (!initArrayBuffer(gl, colors, 3, gl.FLOAT, 'a_Color'))
    return -1;

  // Write the indices to the buffer object
  gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer);
  gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW);

  return indices.length;
}

function initArrayBuffer(gl, data, num, type, attribute) {
  // Create a buffer object
  var buffer = gl.createBuffer();
  if (!buffer) {
    console.log('Failed to create the buffer object');
    return false;
  }
  // Write date into the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
  gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);
　// Assign the buffer object to the attribute variable
  var a_attribute = gl.getAttribLocation(gl.program, attribute);
  if (a_attribute < 0) {
    console.log('Failed to get the storage location of ' + attribute);
    return false;
  }
  gl.vertexAttribPointer(a_attribute, num, type, false, 0, 0);
  // Enable the assignment of the buffer object to the attribute variable
  gl.enableVertexAttribArray(a_attribute);

  gl.bindBuffer(gl.ARRAY_BUFFER, null);

  return true;
}

光照

光照原理

现实世界中的物体被光线照射时,会反射一部分光。只有当反射光线进入你的眼睛时.你才能够看到物体并辩认出它的颜色比如，白色的盒子会反射白光，当白光进入你的眼睛时，你才能看到盒子是白色的。

在现实世界中，当光线照射到物体上时，发生了两个重要的现象 (见图 8.1):

根据光源和光线方向，物体不同表面的明暗程度变得不一致。

根据光源和光线方向，物体向地面投下了影子。

在生活中，你可能常常会注意到阴影，却很少注意到明暗差异。实际上正是明暗差异给了物体立体感，虽然难以察觉，但它始终存在。虽然图 8.1 所示的立方体是纯白色的,但我们还是能够辨认它的每个面，因为它的每个面受到光照的程度不同。如你所见，向着光的表面看上去明亮一些，而侧着光或背着光的表面看上去就暗一些。正是有了这些差异，立方体看上去才真正像一个立方体。

在三维图形学中术语着色'(shading)的真正含义就是，根据光照条件重建“物体各表面明暗不一的效果”的过程。物体向地面投下影子的现象又被称为阴影(shadowing)本节将讨论前者，而后者则留到第 10 章再讨论 (那一章将基于 WebGL 的基础知识讨论系列有用的高级技术)。

在讨论着色过程之前，考虑两件事：

发出光线的光源的类型。

物体表面如何反射光线。

在开始编写代码之前，我们先来理解一下上述两个问题。

光源类型

当物体被光线射击时，必然存在发出光线的光源。真实世界中的光主要有两种类型:

平行光(directional light)，类似于自然中的太阳光；

点光源光(point light)，类似于人造灯泡的光。

此外，我们还用环境光(ambient light) 来模拟真实世界中的非直射光 (也就是由光源发出后经过墙壁或其他物体反射后的光)。

三维图形学还使用一些其他类型的光，比如用聚光灯光 (spot light) 来模拟电筒、车前灯等。本书只讨论前三种基本类型的光，至于其他的更加特殊的光源类型，可以参考 OpenGL ES2.0 Programming Guide 一书。

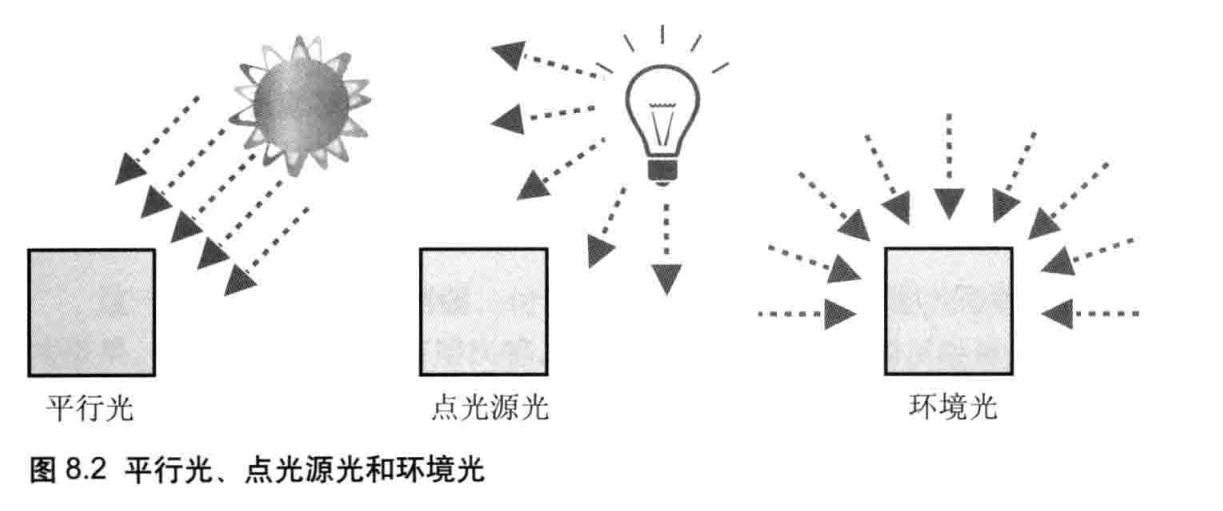
本书讨论以下三种类型的光源。

平行光：顾名思义，平行光的光线是相互平行的，平行光具有方向。平行光可以看作是无限远处的光源 (比如太阳)发出的光。因为太阳距离地球很远，所以阳光到达地球时可以认为是平行的。平行光很简单，可以用一个方向和一个颜色来定义。

点光源光 ：点光源光是从一个点向周围的所有方向发出的光。点光源光可以用来表示现实中的灯泡、火焰等。我们需要指定点光源的位置和颜色”。光线的方向将根据点光源的位置和被照射之处的位置计算出来，因为点光源的光线的方向在场景内的不同位置是不同的。

环境光：环境光 (间接光)是指那些经光源 (点光源或平行光源)发出后，被墙壁环境光等物体多次反射，然后照到物体表面上的光。环境光从各个角度照射物体，其强度都是一致的。比如说,在夜间打开冰箱的门,整个厨房都会有些微微亮,这就是环境光的作用。环境光不用指定位置和方向，只需要指定颜色即可。

反射类型

物体向哪个方向反射光，反射的光是什么颜色，决于以下两个因素 :入射光和物取体表面的类型。入射光的信息包括入射光的方向和颜色，而物体表面的信息包括表面的固有颜色 (也称基底色)和反射特性。

物体表面反射光线的方式有两种:漫反射(diffuse refiection)和环境反射(enviromentambient reflection)。本节的重点是如何根据上述两种信息 (入射光和物体表面特性)来计算出反射光的颜色。本节会涉及一些简单的数学计算。

漫反射

漫反射是针对平行光或点光源而言的。漫反射的反射光在各个方向上是均匀的，如图 8.3 所示。如果物体表面像镜子一样光滑，那么光线就会以特定的角度反射出去，但是现实中的大部分材质，比如纸张、岩石、塑料等，其表面都是粗糙的，在这种情况下反射光就会以不固定的角度反射出去。漫反射就是针对后一种情况而建立的理想反射模型。

在漫反射中，反射光的颜色取决于人射光的颜色、表面的基底色、入射光与表面形成的入射角。我们将入射角定义为入射光与表面的法线形成的夹角，并用θ表示，那么漫反射的颜色可以根据下式计算得到：

式子中，<入射光颜色>指的是点光源或平行光的颜色，乘法操作是在颜色矢量上逐分量 (R、G、B)进行的。因为漫反射光在各个方向上都是“均匀”的，所以从任何角度看上去其强度都相等，如图 8.4 所示。

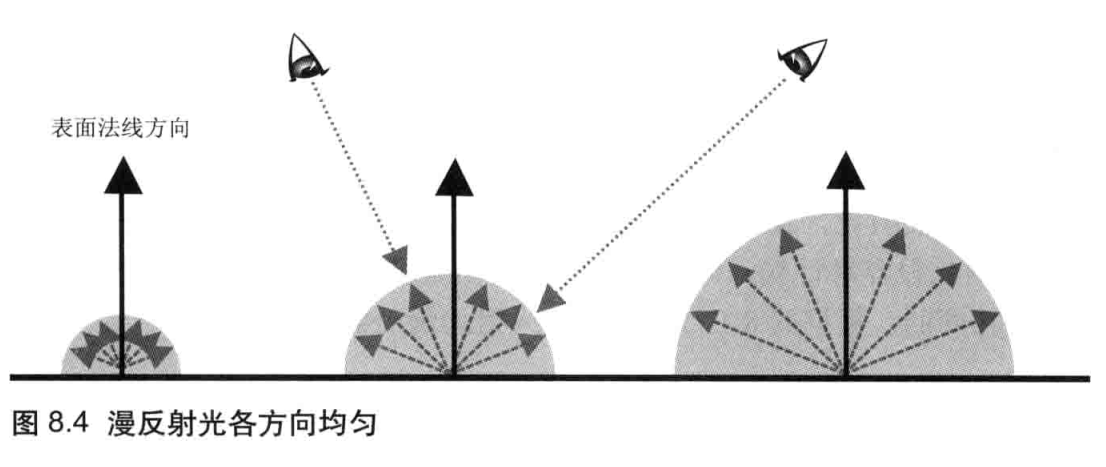
环境反射

环境反射是针对环境光而言的。在环境反射中，反射光的方向可以认为就是入射光的反方向。由于环境光照射物体的方式就是各方向均匀、强度相等的，所以反射光也是各向均匀的，如图 8.5 所示。我们可以这样来描述它 :

这里的< 入射光颜色 > 实际上也就是环境光的颜色

当漫反射和环境反射同时存在时,将两者加起来,就会得到物体最终被观察到的颜色：

注意，两种反射光并不一定总是存在，也并不一定要完全按照上述公式来计算。渲染三维模型时，你可以修改这些公式以达到想要的效果。

平行光下的漫反射

如前所述，漫反射的反射光，其颜色与人射光在人射点的人射角θ有关。平行光入射产生的漫反射光的颜色很容易计算，因为平行光的方向是唯一的，对于同一个平面上的所有点，入射角是相同的。根据式 8.1 计算平行光人射的漫反射光颜色。

<漫反射光颜色>=<入射光颜色>x<表面基底色>x cosθ

上式用到了三项数据 :

平行人射光的颜色

表面的基底色

入射光与表面形成的人射角 0

入射光的颜色可能是白色的，比如阳光，也可能是其他颜色的，比如隧道中的橘黄色灯光。我们知道颜色可以用 RGB 值来表示，比如标准强度的白光颜色值就是 (1.0,1.01.0)。物体表面的基底色其实就是“物体本来的颜色”(或者说是“物体在标准白光下的颜色”)。按照式 8.1 计算反射光颜色时，我们对 RGB 值的三个分量逐个相乘。

假设入射光是白色(1.0,1.0,1.0)，而物体表面的基底色是红色 (1.0,0.0,0.0)，而人射角 0 为0.0(即人射光垂直人射)，根据式 8.1，入射光的红色分量R为1.0，基底色的红色分量R为1.0，人射角余弦值 cos 为 1.0，那么反射光的红色分量R就可以有如下计算得到 :

R=1.0*1.0*1.0=1.0
类似地，我们可以算出绿色分量 G 和蓝色分量 B

G-1.0*0.0*1.0=0.0
B=1.0*0.0*1.0=0.0

根据上面的计算，当白光垂直人射到红色物体的表面时，漫反射光的颜色就变成了红色(1.0,0.0,0.0)。而如果是红光垂直人射到白色物体的表面时，漫反射光的颜色也会是红色。在这两种情况下，物体在观察者看来就是红色的，这很符合我们在现实世界中的经验。

那么如果人射角 0 是 90 度，也就是说人射光与表面平行，一点都没有“照射”到表面上，在这种情况下会怎样呢?根据我们在现实世界中的经验，物体表面应该完全不反光，看上去是黑的。验证一下:当 θ是 90 度的时候，cosθ 的值是 0，那么根据上面的式子，不管人射光的颜色和物体表面基底色是什么，最后得到的漫反射光颜色都为(0.00.0,0.0)，也就是黑色，正如我们预期的那样。同样，如果 θ 60 度，也就是斜射平行光斜射到物体表面上，那么该表面应该还是红色的，只不过比垂直入射时暗一些。根据上式，cosθ 0.5，漫反射光颜色为(0.5,0.0,0.0)，即暗红色。

这个简单的例子帮助你了解了如何计算漫反射光的颜色。但是我们并不知道人射角θ 是多少，只知道光线的方向。下面我们就来通过光线和物体表面的方向来计算入射角 θ，将式 8.1 中的θ换成我们更加熟悉的东西。

根据光线和表面的方向计算入射角

在程序中，我们没法像前一节最后那样，直接说“人射角是多少多少度”。我们必须根据人射光的方向和物体表面的朝向 (即法线方向)来计算出人射角。这并不简单.因为在创建三维模型的时候，我们无法预先确定光线将以怎样的角度照射到每个表面上但是，我们可以确定每个表面的朝向。在指定光源的时候，再确定光的方向，就可以用这两项信息来计算出人射角了。

幸运的是，我们可以通过计算两个矢量的点积，来计算这两个矢量的夹角余弦值cos0。点积运算的使用非常频繁,GLSLES内置了点积运算函数。在公式中,我们使用点符号·来表示点积运算。这样，cos 0 就可以通过下式计算出来:

cos0 =<光线方向>·<法线方向>

因此，式 8.1 可以改写成式 8.4，如下所示 :

这里有两点需要注意:

其一：光线方向矢量和表面法线矢量的长度必须为 1，否则反射光的颜色就会过暗或过亮。将一个矢量的长度调整为 1,同时保持方向不变的过程称之为归一化 (normalization)GLSL ES 提供了内置的归一化函数，你可以直接使用。

其二，这里 (包括后面)所谓的“光线方向”，实际上是入射方向的反方向，即从人射点指向光源方向 (因为这样，该方向与法线方向的夹角才是人射角)，如图 8.6 所示。

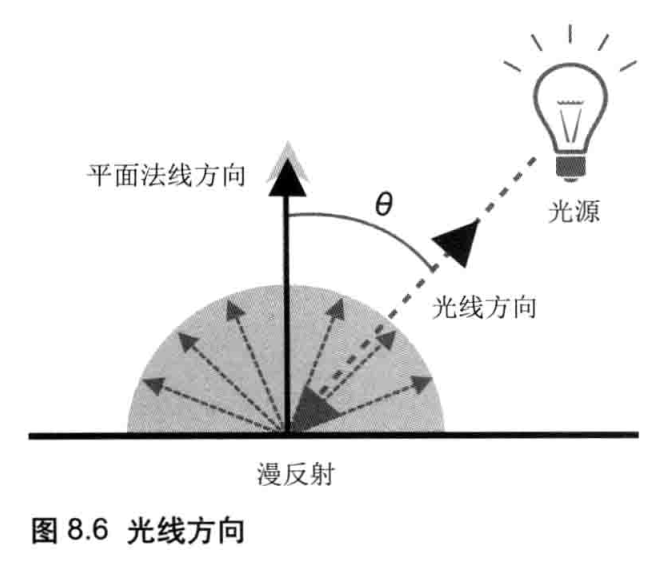
这里用到了表面的法线方向来参与对 θ 的计算，可是我们还不知道法线方向，下一节就来研究如何获取表面的法线方向。

法线：表面的朝向

物体表面的朝向，即垂直于表面的方向，又称法线或法向量。法向量有三个分量，向量 (nx,ny,nz)表示从原点 (0,0,0) 指向点 (nx,ny,nz)的方向。比如说，向量(1,0,0)表示x轴正方向，向量(0,0,1)表示z轴正方向。涉及到表面和法向量的问题时，必须考虑以下两点：

一个表面具有两个法向量

每个表面都有两个面，“正面”和“背面”。两个面各自具有一个法向量。比如，垂直于z轴的x-y 平面，其背面的法向量为z正半轴，即(0,0,1)，如图 8.7 (左)所示;而背面的法向量为z负半轴，即(0,0,-1)，如图 8.7 (右)所示。

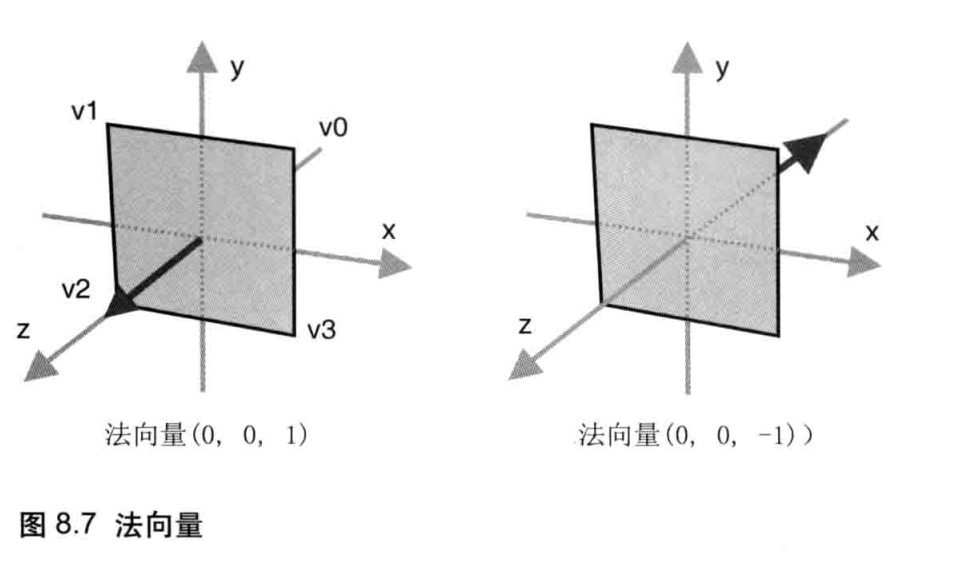
在三维图形学中，表面的正面和背面取决于绘制表面时的顶点顺序。当你按照 v0，v2，v3 的顶点顺序绘制了一个平面，那么当你从正面观察这个表面时，这 4个顶点是顺时针的，而你从背面观察该表面，这4个顶点就是逆时针的 (即第 3 章中用来确定旋转方向的“右手法则”)。如图 8.7 所示，该平面正面的法向量是(0,0,-1)。

平面的法向量唯一

由于法向量表示的是方向，与位置无关，所以一个平面只有一个法向量。换句话说平面的任意一点都具有相同的法向量。

进一步来说，即使有两个不同的平面，只要其朝向相同 (也就是两个平面平行)，法向量也相同。比方说，有一个经过点(10,98,9)的平面，只要它垂直于z轴，它的法向量仍然是(0,0,1)和(0,0,-1)，和经过原点并垂直于 z轴的平面一样，如图 8.8 所示。

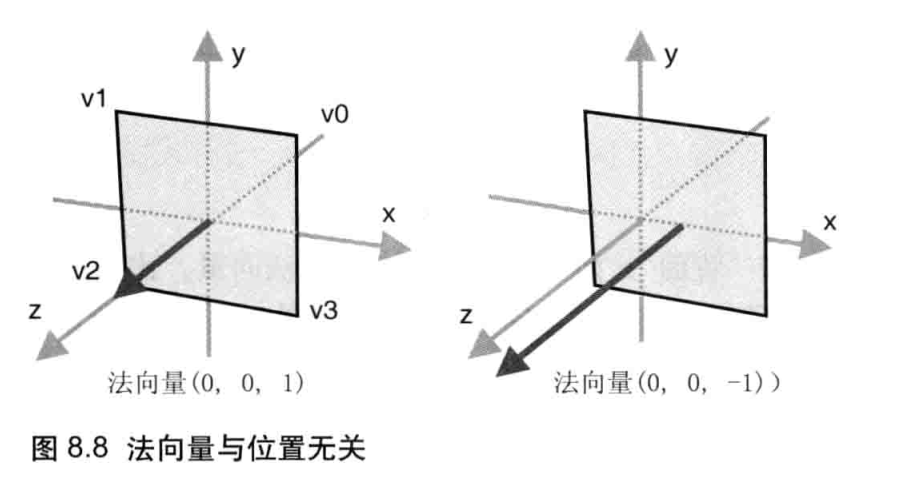
图 8.9(左)显示了示例程序中的立方体及每个表面的法向量。比如立方体表面上的法向量表示为 n(0,1,0)。

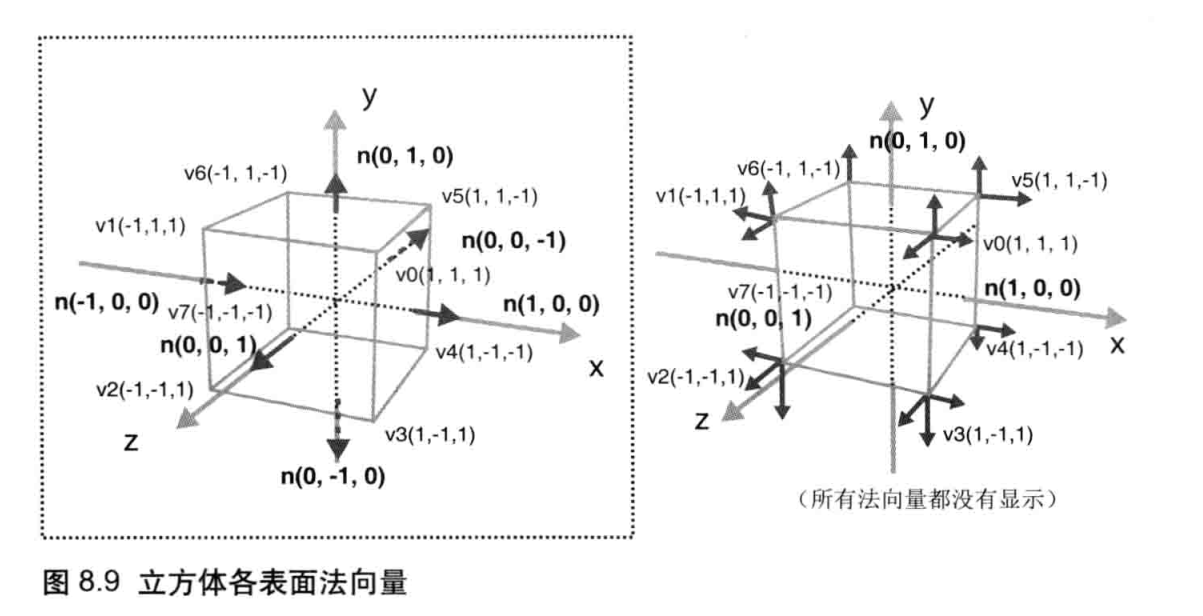
一旦计算好每个平面的法向量，接下来的任务就是将数据传给着色器程序。以前的程序把颜色作为“逐顶点数据”存储在缓冲区中，并传给着色器。对法向量数据也可以这样做。如图 8.9(右)所示，每个顶点对应 3 个法向量，就像之前每个顶点都对应3 个颜色值一样

注意

立方体比较特殊，各表面垂直相交，所以每个顶点对应了个法向量 (同时在缓冲区中被拆成 3个顶点)。但是，一些表面光滑的物体，比如游戏中的人物模型，通常其每个顶点只对应1个法向量。

示例程序 Lightedcube 显示了一个处于白色平行光照射下的红色三角形，如图 8.10所示。

// LightedCube.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE = 
  'attribute vec4 a_Position;\n' + 
  'attribute vec4 a_Color;\n' + 				// 表面基底色
  'attribute vec4 a_Normal;\n' +        // 法向量
  'uniform mat4 u_MvpMatrix;\n' +
  'uniform vec3 u_LightColor;\n' +     // 光线颜色
  'uniform vec3 u_LightDirection;\n' + //	归一化的世界坐标
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_MvpMatrix * a_Position ;\n' +
  // 对法向量进行归一化
  '  vec3 normal = normalize(a_Normal.xyz);\n' +
  // 计算光线方向和法向量的点极
  '  float nDotL = max(dot(u_LightDirection, normal), 0.0);\n' +
  // 计算漫反射光的颜色
  '  vec3 diffuse = u_LightColor * a_Color.rgb * nDotL;\n' +
  '  v_Color = vec4(diffuse, a_Color.a);\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE = 
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // 设置顶点的坐标，颜色和法向量
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Set the clear color and enable the depth test
  gl.clearColor(0, 0, 0, 1);
  gl.enable(gl.DEPTH_TEST);

  // Get the storage locations of uniform variables and so on
  var u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
  var u_LightColor = gl.getUniformLocation(gl.program, 'u_LightColor');
  var u_LightDirection = gl.getUniformLocation(gl.program, 'u_LightDirection');
  if (!u_MvpMatrix || !u_LightColor || !u_LightDirection) { 
    console.log('Failed to get the storage location');
    return;
  }

  // 设置光线颜色为白色
  gl.uniform3f(u_LightColor, 1.0, 1.0, 1.0);
  // 设置光线方向（世界坐标系下的）
  var lightDirection = new Vector3([0.5, 3.0, 4.0]);
  lightDirection.normalize();     // 归一化
  gl.uniform3fv(u_LightDirection, lightDirection.elements);

  // Calculate the view projection matrix
  var mvpMatrix = new Matrix4();    // Model view projection matrix
  mvpMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);
  mvpMatrix.lookAt(3, 3, 7, 0, 0, 0, 0, 1, 0);
  // Pass the model view projection matrix to the variable u_MvpMatrix
  gl.uniformMatrix4fv(u_MvpMatrix, false, mvpMatrix.elements);

  // Clear color and depth buffer
  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

  gl.drawElements(gl.TRIANGLES, n, gl.UNSIGNED_BYTE, 0);   // Draw the cube
}

function initVertexBuffers(gl) {
  // Create a cube
  //    v6----- v5
  //   /|      /|
  //  v1------v0|
  //  | |     | |
  //  | |v7---|-|v4
  //  |/      |/
  //  v2------v3
  var vertices = new Float32Array([   // 顶点坐标
     1.0, 1.0, 1.0,  -1.0, 1.0, 1.0,  -1.0,-1.0, 1.0,   1.0,-1.0, 1.0, // v0-v1-v2-v3 front
     1.0, 1.0, 1.0,   1.0,-1.0, 1.0,   1.0,-1.0,-1.0,   1.0, 1.0,-1.0, // v0-v3-v4-v5 right
     1.0, 1.0, 1.0,   1.0, 1.0,-1.0,  -1.0, 1.0,-1.0,  -1.0, 1.0, 1.0, // v0-v5-v6-v1 up
    -1.0, 1.0, 1.0,  -1.0, 1.0,-1.0,  -1.0,-1.0,-1.0,  -1.0,-1.0, 1.0, // v1-v6-v7-v2 left
    -1.0,-1.0,-1.0,   1.0,-1.0,-1.0,   1.0,-1.0, 1.0,  -1.0,-1.0, 1.0, // v7-v4-v3-v2 down
     1.0,-1.0,-1.0,  -1.0,-1.0,-1.0,  -1.0, 1.0,-1.0,   1.0, 1.0,-1.0  // v4-v7-v6-v5 back
  ]);


  var colors = new Float32Array([    // Colors
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v1-v2-v3 front
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v3-v4-v5 right
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v5-v6-v1 up
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v1-v6-v7-v2 left
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v7-v4-v3-v2 down
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0　    // v4-v7-v6-v5 back
 ]);


  var normals = new Float32Array([    // 法向量
    0.0, 0.0, 1.0,   0.0, 0.0, 1.0,   0.0, 0.0, 1.0,   0.0, 0.0, 1.0,  // v0-v1-v2-v3 front
    1.0, 0.0, 0.0,   1.0, 0.0, 0.0,   1.0, 0.0, 0.0,   1.0, 0.0, 0.0,  // v0-v3-v4-v5 right
    0.0, 1.0, 0.0,   0.0, 1.0, 0.0,   0.0, 1.0, 0.0,   0.0, 1.0, 0.0,  // v0-v5-v6-v1 up
   -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  // v1-v6-v7-v2 left
    0.0,-1.0, 0.0,   0.0,-1.0, 0.0,   0.0,-1.0, 0.0,   0.0,-1.0, 0.0,  // v7-v4-v3-v2 down
    0.0, 0.0,-1.0,   0.0, 0.0,-1.0,   0.0, 0.0,-1.0,   0.0, 0.0,-1.0   // v4-v7-v6-v5 back
  ]);


  // Indices of the vertices
  var indices = new Uint8Array([
     0, 1, 2,   0, 2, 3,    // front
     4, 5, 6,   4, 6, 7,    // right
     8, 9,10,   8,10,11,    // up
    12,13,14,  12,14,15,    // left
    16,17,18,  16,18,19,    // down
    20,21,22,  20,22,23     // back
 ]);


  // Write the vertex property to buffers (coordinates, colors and normals)
  if (!initArrayBuffer(gl, 'a_Position', vertices, 3, gl.FLOAT)) return -1;
  if (!initArrayBuffer(gl, 'a_Color', colors, 3, gl.FLOAT)) return -1;
  if (!initArrayBuffer(gl, 'a_Normal', normals, 3, gl.FLOAT)) return -1;

  // Write the indices to the buffer object
  var indexBuffer = gl.createBuffer();
  if (!indexBuffer) {
    console.log('Failed to create the buffer object');
    return false;
  }

  gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer);
  gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW);

  return indices.length;
}

function initArrayBuffer (gl, attribute, data, num, type) {
  // Create a buffer object
  var buffer = gl.createBuffer();
  if (!buffer) {
    console.log('Failed to create the buffer object');
    return false;
  }
  // Write date into the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
  gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);
  // Assign the buffer object to the attribute variable
  var a_attribute = gl.getAttribLocation(gl.program, attribute);
  if (a_attribute < 0) {
    console.log('Failed to get the storage location of ' + attribute);
    return false;
  }
  gl.vertexAttribPointer(a_attribute, num, type, false, 0, 0);
  // Enable the assignment of the buffer object to the attribute variable
  gl.enableVertexAttribArray(a_attribute);

  gl.bindBuffer(gl.ARRAY_BUFFER, null);

  return true;
}

注意，顶点着色器实现了式 8.4 :

<漫反射光颜色>-<入射光颜色>x<表面基底色>x(<光线方向>·<法线方向>)

计算漫反射光颜色需要 :

(1) 入射光颜色，(2) 表面基底色，(3) 入射光方向，(4) 表面法线方向。其中后两者都必须是归一化的 (即长度为 1.0)。

顶点着色器

顶点着色器中的 a_color 变量表示表面基底色，a_Normal 变量表示表面法线方向，u_Lightcolor 变量表示人射光颜色，u LightDirection 变量表示人射光方向。注意，人射光方向u LightDirection 是在世界坐标系下的"，而且在传入着色器前已经在 JavaScript 中归一化了。这样，我们就可以避免在顶点着色器每次执行时都对它进行归一化。

GLSL ES 提供的内置函数 dot())计算两个矢量的点积< 光线方向 >·< 法线方向 >，该函数接收两个矢量作为参数，返回它们的点积

如果点积大于 0，就将点积赋值给 nDotu 变量，如果其小于 0，就将 0 赋给该变量。使用内置函数 max()完成这个任务，将点积和 0两者中的较大者赋值给 nDotI。

点积值小于 0,意味着 cos 中的 0 大于 90 度。0 是人射角,也就是人射反方向 (光线方向)与表面法向量的夹角，0 大于90 度说明光线照射在表面的背面上,如图 8.11所示。此时，将 nDotL 赋为 0.0。

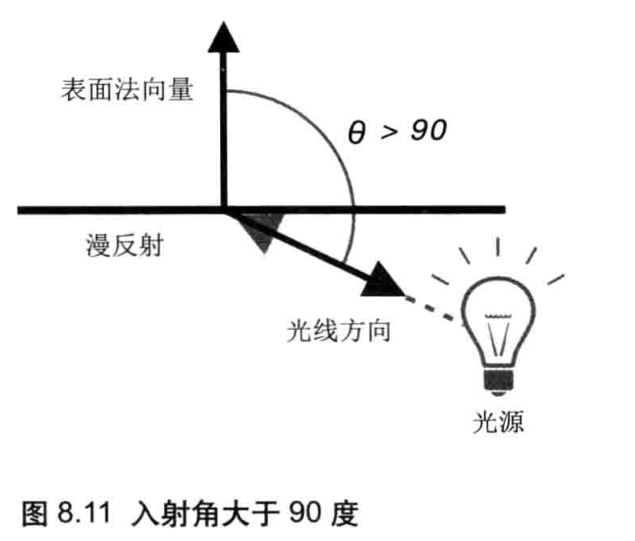
现在准备工作都已经就绪了，我们在顶点着色器中直接计算式 8.4。注意a_color 变量即顶点的颜色，被从 vec4 对象转成了 vec3 对象，因为其第 4个分量(透明度)与式 8.4 无关。
实际上，物体表面的透明度确实会影响物体的外观。但这时光照的计算较为复杂,现在暂时认为物体都是不透明的，这样就计算出了漫反射光的颜色 diffuse 。

然后，将 diffuse 的值赋给v_color 变量。v_color 是 vec4 对象，而diffuse 是 vec3 对象，需要将第 4分量补上为 1.0。

顶点着色器运行的结果就是计算出了v_color 变量，其值取决于顶点的颜色、法线方向、平行光的颜色和方向。v_color 变量将被传人片元着色器并赋值给 gl_FragColor变量。本例中的光是平行光，所以立方体上同一个面的颜色也是一致的，没有之前出现的颜色渐变效果。

JavaScript 程序流程

JavaScript将光的颜色u_LightColor 和方向u_LightDirection 传给顶点着色器。首先用 gl.uniform3f() 函数将u_Lightcolor 赋值为(1.0,1.0,1.0)，表示人射光是白光。

下一步是设置光线方向，注意光线方向必须被归一化。cuon-matrix.js 为 Vector3类型提供了 normalize() 函数，以实现归一化。该函数的用法非常简单:在你想要进行归一化的 Vector3 对象上调用 normalize() 函数即可 (第73行)。注意 JavaScript和GLSL ES 中对矢量进行归一化的不同之处。

  // 设置光线方向（世界坐标系下的）
  var lightDirection = new Vector3([0.5, 3.0, 4.0]);
  lightDirection.normalize();     // 归一化
  gl.uniform3fv(u_LightDirection, lightDirection.elements);

归一化后的光线方向以 Eloat32Array 类型的形式存储在 lightDirection 对象的elements属性中,使用gl.uniform3fv()将其分配给着色器中的u_LightDirection变量。

最后，在 initVertexBuffers() 函数中为每个顶点定义法向量(就像以前在coloredcube.js 中为每个顶点定义颜色一样)。法向量数据存储在 normals 数组中,然后被 initArrayBuffer() 函数传给了顶点着色器的a_Normal变量。

  if (!initArrayBuffer(gl, 'a_Normal', normals, 3, gl.FLOAT)) return -1;

initArrayBuffer() 函数的作用是将第3个参数指定的数组 (normals)分配给第2个参数指定的着色器中的变量。该函数在 coloredCube 中已经出现过了。

环境光下的漫反射

现在，我们已经成功实现了平行光下的漫反射光，LightedCube 的效果如图 8.11 所示但是图 8.11 和现实中的立方体还是有点不大一样，特别是右侧表面是全黑的，仿佛不存在一样。

虽然程序是严格按照式 8.4 对场景进行光照的，但经验告诉我们肯定有什么地方不对劲。在现实世界中，光照下物体的各表面的差异不会如此分明:那些背光的面虽然会暗一些，但绝不至于黑到看不见的程度。实际上，那些背光的面是被非直射光(即其他物体，如墙壁的反射光等)照亮的，前面提到的环境光就起到了这部分非直射光的作用,它使场景更加逼真。因为环境光均匀地从各个角度照在物体表面，所以由环境光反射产生的颜色只取决于光的颜色和表面基底色，使用式 8.2 计算后我们再来看一下:

<环境反射光颜色>=<入射光颜色>X<表面基底色>

接下来，向示例程序中加人上式中的环境光所产生的反射光颜色，如式 8.3 所示 :

<表面的反射光颜色>=<漫反射光颜色>+<环境反射光颜色>

环境光是由墙壁等其他物体反射产生的，所以环境光的强度通常比较弱。假设环境光是较弱的白光(0.2,0.2,0.2)，而物体表面是红色的(1.0,0.0,0.0)。根据式 8.2，由环境光产生的反射光颜色就是暗红色(0.2,0.0,0.0)。同样,在蓝色的房间中,环境光为(0.0,0.00.2)，有一个白色的物体，即表面基底色为(1.0,1.0,1.0)，那么由环境光产生的漫反射光颜色就是淡蓝色(0.0,0.0,0.2)。

示例程序 LightedCube_ambient 实现了环境光漫反射的效果，如图 8.13 所示。可见完全没有被平行光照到的表面也不是全黑，而是呈现较暗的颜色，与真实世界更加相符。

// LightedCube_ambient.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'attribute vec4 a_Normal;\n' +       // Normal
  'uniform mat4 u_MvpMatrix;\n' +
  'uniform vec3 u_DiffuseLight;\n' +   // Diffuse light color
  'uniform vec3 u_LightDirection;\n' + // Diffuse light direction (in the world coordinate, normalized)
  'uniform vec3 u_AmbientLight;\n' +   // 环境光颜色
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_MvpMatrix * a_Position;\n' +
     // Make the length of the normal 1.0
  '  vec3 normal = normalize(a_Normal.xyz);\n' +
     // The dot product of the light direction and the normal (the orientation of a surface)
  '  float nDotL = max(dot(u_LightDirection, normal), 0.0);\n' +
     // Calculate the color due to diffuse reflection
  '  vec3 diffuse = u_DiffuseLight * a_Color.rgb * nDotL;\n' +
     // 计算环境光产生的反射光颜色
  '  vec3 ambient = u_AmbientLight * a_Color.rgb;\n' +
     // 将以上两者相加得到物体最终的颜色
  '  v_Color = vec4(diffuse + ambient, a_Color.a);\n' + 
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // 
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Set the clear color and enable the depth test
  gl.clearColor(0, 0, 0, 1);
  gl.enable(gl.DEPTH_TEST);

  // Get the storage locations of uniform variables and so on
  var u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
  var u_DiffuseLight = gl.getUniformLocation(gl.program, 'u_DiffuseLight');
  var u_LightDirection = gl.getUniformLocation(gl.program, 'u_LightDirection');
  var u_AmbientLight = gl.getUniformLocation(gl.program, 'u_AmbientLight');
  if (!u_MvpMatrix || !u_DiffuseLight || !u_LightDirection || !u_AmbientLight) { 
    console.log('Failed to get the storage location');
    return;
  }

  // Set the light color (white)
  gl.uniform3f(u_DiffuseLight, 1.0, 1.0, 1.0);
  // Set the light direction (in the world coordinate)
  var lightDirection = new Vector3([0.5, 3.0, 4.0]);
  lightDirection.normalize();     // Normalize
  gl.uniform3fv(u_LightDirection, lightDirection.elements);
  // 传入环境光颜色
  gl.uniform3f(u_AmbientLight, 0.2, 0.2, 0.2);

  // Calculate the view projection matrix
  var mvpMatrix = new Matrix4();  // Model view projection matrix
  mvpMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);
  mvpMatrix.lookAt(3, 3, 7, 0, 0, 0, 0, 1, 0);
  // Pass the model view projection matrix to the variable u_MvpMatrix
  gl.uniformMatrix4fv(u_MvpMatrix, false, mvpMatrix.elements);

  // Clear color and depth buffer
  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

  // Draw the cube
  gl.drawElements(gl.TRIANGLES, n, gl.UNSIGNED_BYTE, 0);
}

function initVertexBuffers(gl) {
  // Create a cube
  //    v6----- v5
  //   /|      /|
  //  v1------v0|
  //  | |     | |
  //  | |v7---|-|v4
  //  |/      |/
  //  v2------v3
  // Coordinates
  var vertices = new Float32Array([
     1.0, 1.0, 1.0,  -1.0, 1.0, 1.0,  -1.0,-1.0, 1.0,   1.0,-1.0, 1.0, // v0-v1-v2-v3 front
     1.0, 1.0, 1.0,   1.0,-1.0, 1.0,   1.0,-1.0,-1.0,   1.0, 1.0,-1.0, // v0-v3-v4-v5 right
     1.0, 1.0, 1.0,   1.0, 1.0,-1.0,  -1.0, 1.0,-1.0,  -1.0, 1.0, 1.0, // v0-v5-v6-v1 up
    -1.0, 1.0, 1.0,  -1.0, 1.0,-1.0,  -1.0,-1.0,-1.0,  -1.0,-1.0, 1.0, // v1-v6-v7-v2 left
    -1.0,-1.0,-1.0,   1.0,-1.0,-1.0,   1.0,-1.0, 1.0,  -1.0,-1.0, 1.0, // v7-v4-v3-v2 down
     1.0,-1.0,-1.0,  -1.0,-1.0,-1.0,  -1.0, 1.0,-1.0,   1.0, 1.0,-1.0  // v4-v7-v6-v5 back
  ]);

  // Colors
  var colors = new Float32Array([
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v1-v2-v3 front
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v3-v4-v5 right
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v5-v6-v1 up
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v1-v6-v7-v2 left
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v7-v4-v3-v2 down
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0　    // v4-v7-v6-v5 back
 ]);

  // Normal
  var normals = new Float32Array([
    0.0, 0.0, 1.0,   0.0, 0.0, 1.0,   0.0, 0.0, 1.0,   0.0, 0.0, 1.0,  // v0-v1-v2-v3 front
    1.0, 0.0, 0.0,   1.0, 0.0, 0.0,   1.0, 0.0, 0.0,   1.0, 0.0, 0.0,  // v0-v3-v4-v5 right
    0.0, 1.0, 0.0,   0.0, 1.0, 0.0,   0.0, 1.0, 0.0,   0.0, 1.0, 0.0,  // v0-v5-v6-v1 up
   -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  // v1-v6-v7-v2 left
    0.0,-1.0, 0.0,   0.0,-1.0, 0.0,   0.0,-1.0, 0.0,   0.0,-1.0, 0.0,  // v7-v4-v3-v2 down
    0.0, 0.0,-1.0,   0.0, 0.0,-1.0,   0.0, 0.0,-1.0,   0.0, 0.0,-1.0   // v4-v7-v6-v5 back
  ]);

  // Indices of the vertices
  var indices = new Uint8Array([
     0, 1, 2,   0, 2, 3,    // front
     4, 5, 6,   4, 6, 7,    // right
     8, 9,10,   8,10,11,    // up
    12,13,14,  12,14,15,    // left
    16,17,18,  16,18,19,    // down
    20,21,22,  20,22,23     // back
 ]);

  // Write the vertex property to buffers (coordinates, colors and normals)
  if (!initArrayBuffer(gl, 'a_Position', vertices, 3)) return -1;
  if (!initArrayBuffer(gl, 'a_Color', colors, 3)) return -1;
  if (!initArrayBuffer(gl, 'a_Normal', normals, 3)) return -1;

  // Unbind the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, null);

  // Write the indices to the buffer object
  var indexBuffer = gl.createBuffer();
  if (!indexBuffer) {
    console.log('Failed to create the buffer object');
    return false;
  }
  gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer);
  gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW);

  return indices.length;
}

function initArrayBuffer(gl, attribute, data, num) {
  // Create a buffer object
  var buffer = gl.createBuffer();
  if (!buffer) {
    console.log('Failed to create the buffer object');
    return false;
  }
  // Write date into the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
  gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);
  // Assign the buffer object to the attribute variable
  var a_attribute = gl.getAttribLocation(gl.program, attribute);
  if (a_attribute < 0) {
    console.log('Failed to get the storage location of ' + attribute);
    return false;
  }
  gl.vertexAttribPointer(a_attribute, num, gl.FLOAT, false, 0, 0);
  // Enable the assignment of the buffer object to the attribute variable
  gl.enableVertexAttribArray(a_attribute);

  return true;
}

顶点着色器中新增了u_AmbientLight 变量用来接收环境光的颜色值接着根据式 8.2，使用该变量和表面的基底色 a color 计算出反射光的颜色，将其存储在ambient 变量中。这样我们就即有环境光反射产生的颜色 ambient，又有了由平行光漫反射产生的颜色 diffuse。最后根据式 8.3 计算物体最终的颜色并存储在v_color 变量中，作为物体表面最终显示出的颜色，和Lightedcube 一样。

如你所见，与LightedCube 相比，本例对顶点着色器的v_Color 变量加上了 ambier变量，就使得整个立方体变亮了一些，这正是环境光从各个方向均匀照射立方体上产生的。

到目前为止，在本章的示例中，立方体都是静止不动的。事实上，场景中的物体很有可能会运动，观察者的视角也很可能会改变，我们必须考虑这种情况。在第 4章中曾讨论过，物体平移、缩放、旋转都可以用坐标变换来表示。显然，物体的运动会改变每个表面的法向量，从而导致光照效果发生变化。下面就来研究如何实现这一点。

运动物体的光照效果

立方体旋转时，每个表面的法向量也会随之变化。在图 8.15 中，我们沿着z轴负方句观察一个立方体，最左边是立方体的初始状态，图中标出了立方体右侧面的法向量(1.0))，它指向x轴正方向，然后对该立方体进行变换，观察右侧面法向量随之变化的情况。

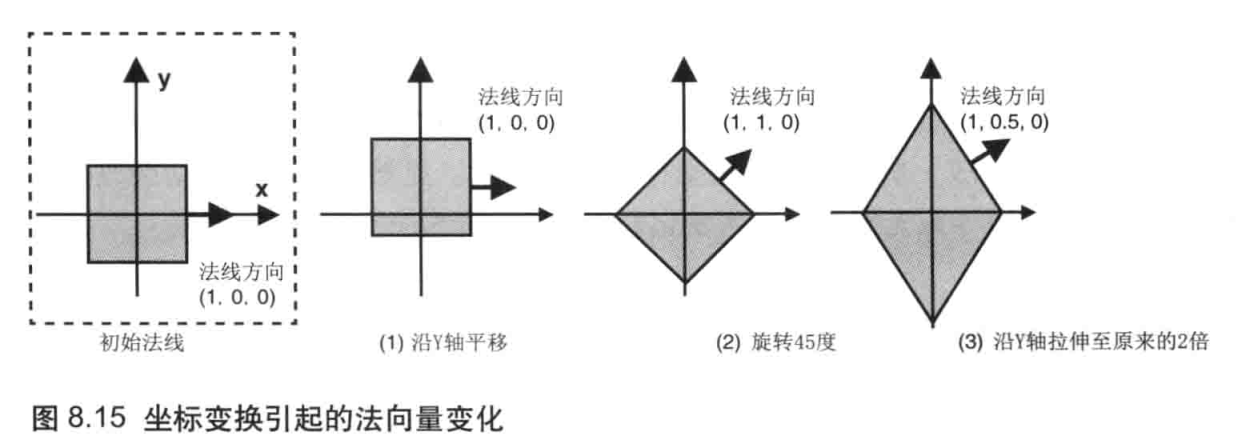
由图 8.15 可知 :

平移变换不会改变法向量，因为平移不会改变物体的方向。

旋转变换会改变法向量，因为旋转改变了物体的方向。

缩放变换对法向量的影响较为复杂。如你所见，最右侧的图显示了立方体先旋转了 45 度，再在y轴上拉伸至原来的2 倍的情况。此时法向量改变了，因为表面的朝向改变了。但是，如果缩放比例在所有的轴上都一致的话，那么法向量就不会变化。最后,即使物体在某些轴上的缩放比例并不一致,法向量也并不一定会变化,比如将最左侧图中的立方体在y轴方向上拉伸两倍，法向量就不会变化。

显然，在对物体进行不同变换时，法向量的变化情况较为复杂 (特别是缩放变换时)。这时候，数学公式就会派上用场了。

魔法矩阵：逆转置矩阵

在第 4章中曾讨论过，对顶点进行变换的矩阵称为模型矩阵。如何计算变换之后的法向量呢?只要将变换之前的法向量乘以模型矩阵的逆转置矩阵(inverse transpose matrix) 即可。所谓逆转置矩阵，就是逆矩阵的转置。

如果矩阵 M 的逆矩阵是 R,那么 R*M 或 M*R 的结果都是单位矩阵。逆矩阵的含义是，转置的意思是，将矩阵的行列进行调换(看上去就像是沿着左上右下对角线进行了翻转)更详细的内容参见附录E“逆转置矩阵”。这里将逆转置矩阵的用法总结如下

规则:用法向量乘以模型矩阵的逆转置矩阵，就可以求得变换后的法向量。

求逆转值矩阵的两个步骤 :

求原矩阵的逆矩阵

将上一步求得的逆矩阵进行转置。

Matrix4 对象提供了便捷的方法来完成上述任务，如表 8.1 所示

// LightedTranslatedRotatedCube.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'attribute vec4 a_Normal;\n' +
  'uniform mat4 u_MvpMatrix;\n' +
  'uniform mat4 u_NormalMatrix;\n' +   // 用来变换法向量的矩阵
  'uniform vec3 u_LightColor;\n' +     // Light color
  'uniform vec3 u_LightDirection;\n' + // Light direction (in the world coordinate, normalized)
  'uniform vec3 u_AmbientLight;\n' +   // Ambient light color
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_MvpMatrix * a_Position;\n' +
     // 计算变换后的法向量并归一化
  '  vec3 normal = normalize(vec3(u_NormalMatrix * a_Normal));\n' +
     // Calculate the dot product of the light direction and the orientation of a surface (the normal)
  '  float nDotL = max(dot(u_LightDirection, normal), 0.0);\n' +
     // Calculate the color due to diffuse reflection
  '  vec3 diffuse = u_LightColor * a_Color.rgb * nDotL;\n' +
     // Calculate the color due to ambient reflection
  '  vec3 ambient = u_AmbientLight * a_Color.rgb;\n' +
     // Add the surface colors due to diffuse reflection and ambient reflection
  '  v_Color = vec4(diffuse + ambient, a_Color.a);\n' + 
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // 
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Set the clear color and enable the depth test
  gl.clearColor(0, 0, 0, 1);
  gl.enable(gl.DEPTH_TEST);

  // Get the storage locations of uniform variables
  var u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
  var u_NormalMatrix = gl.getUniformLocation(gl.program, 'u_NormalMatrix');
  var u_LightColor = gl.getUniformLocation(gl.program, 'u_LightColor');
  var u_LightDirection = gl.getUniformLocation(gl.program, 'u_LightDirection');
  var u_AmbientLight = gl.getUniformLocation(gl.program, 'u_AmbientLight');
  if (!u_MvpMatrix || !u_NormalMatrix || !u_LightColor || !u_LightDirection || !u_AmbientLight) { 
    console.log('Failed to get the storage location');
    return;
  }

  // Set the light color (white)
  gl.uniform3f(u_LightColor, 1.0, 1.0, 1.0);
  // Set the light direction (in the world coordinate)
  var lightDirection = new Vector3([0.0, 3.0, 4.0]);
  lightDirection.normalize();     // Normalize
  gl.uniform3fv(u_LightDirection, lightDirection.elements);
  // Set the ambient light
  gl.uniform3f(u_AmbientLight, 0.2, 0.2, 0.2);

  var modelMatrix = new Matrix4();  // 模型矩阵
  var mvpMatrix = new Matrix4();    // Model view projection matrix
  var normalMatrix = new Matrix4(); // 用来变换法向量的矩阵

  // Calculate the model matrix
  modelMatrix.setTranslate(0, 0.9, 0); // Translate to the y-axis direction
  modelMatrix.rotate(90, 0, 0, 1);     // Rotate 90 degree around the z-axis
  // Calculate the view projection matrix
  mvpMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);
  mvpMatrix.lookAt(3, 3, 7, 0, 0, 0, 0, 1, 0);
  mvpMatrix.multiply(modelMatrix);
  // Pass the model view projection matrix to u_MvpMatrix
  gl.uniformMatrix4fv(u_MvpMatrix, false, mvpMatrix.elements);

  // 根据模型矩阵计算用来变换法向量的矩阵
  normalMatrix.setInverseOf(modelMatrix);
  normalMatrix.transpose();
  // Pass the transformation matrix for normals to u_NormalMatrix
  gl.uniformMatrix4fv(u_NormalMatrix, false, normalMatrix.elements);

  // Clear color and depth buffer
  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

  // Draw the cube
  gl.drawElements(gl.TRIANGLES, n, gl.UNSIGNED_BYTE, 0);
}

function initVertexBuffers(gl) {
  // Create a cube
  //    v6----- v5
  //   /|      /|
  //  v1------v0|
  //  | |     | |
  //  | |v7---|-|v4
  //  |/      |/
  //  v2------v3
  // Coordinates
  var vertices = new Float32Array([
     1.0, 1.0, 1.0,  -1.0, 1.0, 1.0,  -1.0,-1.0, 1.0,   1.0,-1.0, 1.0, // v0-v1-v2-v3 front
     1.0, 1.0, 1.0,   1.0,-1.0, 1.0,   1.0,-1.0,-1.0,   1.0, 1.0,-1.0, // v0-v3-v4-v5 right
     1.0, 1.0, 1.0,   1.0, 1.0,-1.0,  -1.0, 1.0,-1.0,  -1.0, 1.0, 1.0, // v0-v5-v6-v1 up
    -1.0, 1.0, 1.0,  -1.0, 1.0,-1.0,  -1.0,-1.0,-1.0,  -1.0,-1.0, 1.0, // v1-v6-v7-v2 left
    -1.0,-1.0,-1.0,   1.0,-1.0,-1.0,   1.0,-1.0, 1.0,  -1.0,-1.0, 1.0, // v7-v4-v3-v2 down
     1.0,-1.0,-1.0,  -1.0,-1.0,-1.0,  -1.0, 1.0,-1.0,   1.0, 1.0,-1.0  // v4-v7-v6-v5 back
  ]);

  // Colors
  var colors = new Float32Array([
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v1-v2-v3 front
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v3-v4-v5 right
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v5-v6-v1 up
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v1-v6-v7-v2 left
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v7-v4-v3-v2 down
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0　    // v4-v7-v6-v5 back
 ]);

  // Normal
  var normals = new Float32Array([
    0.0, 0.0, 1.0,   0.0, 0.0, 1.0,   0.0, 0.0, 1.0,   0.0, 0.0, 1.0,  // v0-v1-v2-v3 front
    1.0, 0.0, 0.0,   1.0, 0.0, 0.0,   1.0, 0.0, 0.0,   1.0, 0.0, 0.0,  // v0-v3-v4-v5 right
    0.0, 1.0, 0.0,   0.0, 1.0, 0.0,   0.0, 1.0, 0.0,   0.0, 1.0, 0.0,  // v0-v5-v6-v1 up
   -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  // v1-v6-v7-v2 left
    0.0,-1.0, 0.0,   0.0,-1.0, 0.0,   0.0,-1.0, 0.0,   0.0,-1.0, 0.0,  // v7-v4-v3-v2 down
    0.0, 0.0,-1.0,   0.0, 0.0,-1.0,   0.0, 0.0,-1.0,   0.0, 0.0,-1.0   // v4-v7-v6-v5 back
  ]);

  // Indices of the vertices
  var indices = new Uint8Array([
     0, 1, 2,   0, 2, 3,    // front
     4, 5, 6,   4, 6, 7,    // right
     8, 9,10,   8,10,11,    // up
    12,13,14,  12,14,15,    // left
    16,17,18,  16,18,19,    // down
    20,21,22,  20,22,23     // back
 ]);

  // Write the vertex property to buffers (coordinates, colors and normals)
  if (!initArrayBuffer(gl, 'a_Position', vertices, 3)) return -1;
  if (!initArrayBuffer(gl, 'a_Color', colors, 3)) return -1;
  if (!initArrayBuffer(gl, 'a_Normal', normals, 3)) return -1;

  // Unbind the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, null);

  // Write the indices to the buffer object
  var indexBuffer = gl.createBuffer();
  if (!indexBuffer) {
    console.log('Failed to create the buffer object');
    return false;
  }
  gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer);
  gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW);

  return indices.length;
}

function initArrayBuffer(gl, attribute, data, num) {
  // Create a buffer object
  var buffer = gl.createBuffer();
  if (!buffer) {
    console.log('Failed to create the buffer object');
    return false;
  }
  // Write date into the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
  gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);
  // Assign the buffer object to the attribute variable
  var a_attribute = gl.getAttribLocation(gl.program, attribute);
  if (a_attribute < 0) {
    console.log('Failed to get the storage location of ' + attribute);
    return false;
  }
  gl.vertexAttribPointer(a_attribute, num, gl.FLOAT, false, 0, 0);
  // Enable the assignment of the buffer object to the attribute variable
  gl.enableVertexAttribArray(a_attribute);

  return true;
}

点光源

与平行光相比,点光源光发出的光，在三维空间的不同位置上其方向也不同，如图816所示。所以，在对点光源光下的物体进行着色时，需要在每个入射点计算点光源光在该处的方向。

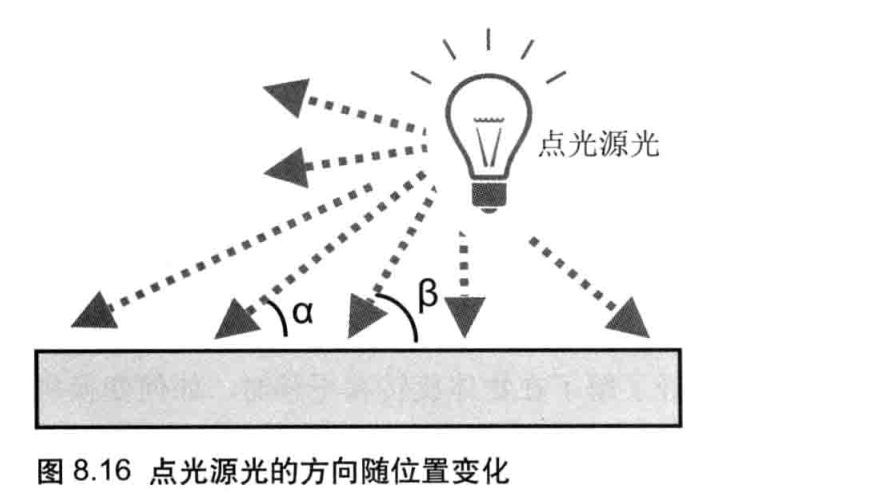
前一节根据每个顶点的法向量和平行光入射方向来计算反射光的颜色。这一节还是采用该方法，只不过点光源光的方向不再是恒定不变的，而要根据每个顶点的位置逐一计算。着色器需要知道点光源光自身的所在位置，而不是光的方方向。

// PointLightedCube.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'attribute vec4 a_Normal;\n' +
  'uniform mat4 u_MvpMatrix;\n' +
  'uniform mat4 u_ModelMatrix;\n' +   // Model matrix
  'uniform mat4 u_NormalMatrix;\n' +  // Transformation matrix of the normal
  'uniform vec3 u_LightColor;\n' +    // Light color
  'uniform vec3 u_LightPosition;\n' + // 光源位置（世界坐标系）
  'uniform vec3 u_AmbientLight;\n' +  // Ambient light color
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_MvpMatrix * a_Position;\n' +
     // Recalculate the normal based on the model matrix and make its length 1.
  '  vec3 normal = normalize(vec3(u_NormalMatrix * a_Normal));\n' +
     // 计算顶点的世界坐标系
  '  vec4 vertexPosition = u_ModelMatrix * a_Position;\n' +
     // 计算光线方向并归一化
  '  vec3 lightDirection = normalize(u_LightPosition - vec3(vertexPosition));\n' +
     // The dot product of the light direction and the normal
  '  float nDotL = max(dot(lightDirection, normal), 0.0);\n' +
     // Calculate the color due to diffuse reflection
  '  vec3 diffuse = u_LightColor * a_Color.rgb * nDotL;\n' +
     // Calculate the color due to ambient reflection
  '  vec3 ambient = u_AmbientLight * a_Color.rgb;\n' +
     //  Add the surface colors due to diffuse reflection and ambient reflection
  '  v_Color = vec4(diffuse + ambient, a_Color.a);\n' + 
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex coordinates, the color and the normal
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Set the clear color and enable the depth test
  gl.clearColor(0.0, 0.0, 0.0, 1.0);
  gl.enable(gl.DEPTH_TEST);

  // Get the storage locations of uniform variables and so on
  var u_ModelMatrix = gl.getUniformLocation(gl.program, 'u_ModelMatrix');
  var u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
  var u_NormalMatrix = gl.getUniformLocation(gl.program, 'u_NormalMatrix');
  var u_LightColor = gl.getUniformLocation(gl.program, 'u_LightColor');
  var u_LightPosition = gl.getUniformLocation(gl.program, 'u_LightPosition');
  var u_AmbientLight = gl.getUniformLocation(gl.program, 'u_AmbientLight');
  if (!u_MvpMatrix || !u_NormalMatrix || !u_LightColor || !u_LightPosition　|| !u_AmbientLight) { 
    console.log('Failed to get the storage location');
    return;
  }

  // Set the light color (white)
  gl.uniform3f(u_LightColor, 1.0, 1.0, 1.0);
  // Set the light direction (in the world coordinate)
  gl.uniform3f(u_LightPosition, 2.3, 4.0, 3.5);
  // Set the ambient light
  gl.uniform3f(u_AmbientLight, 0.2, 0.2, 0.2);

  var modelMatrix = new Matrix4();  // Model matrix
  var mvpMatrix = new Matrix4();    // Model view projection matrix
  var normalMatrix = new Matrix4(); // Transformation matrix for normals

  // Calculate the model matrix
  modelMatrix.setRotate(90, 0, 1, 0); // Rotate around the y-axis
  // Pass the model matrix to u_ModelMatrix
  gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements);

  // Pass the model view projection matrix to u_MvpMatrix
  mvpMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);
  mvpMatrix.lookAt(6, 6, 14, 0, 0, 0, 0, 1, 0);
  mvpMatrix.multiply(modelMatrix);
  gl.uniformMatrix4fv(u_MvpMatrix, false, mvpMatrix.elements);

  // Pass the matrix to transform the normal based on the model matrix to u_NormalMatrix
  normalMatrix.setInverseOf(modelMatrix);
  normalMatrix.transpose();
  gl.uniformMatrix4fv(u_NormalMatrix, false, normalMatrix.elements);

  // Clear color and depth buffer
  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

  // Draw the cube
  gl.drawElements(gl.TRIANGLES, n, gl.UNSIGNED_BYTE, 0);
}

function initVertexBuffers(gl) {
  // Create a cube
  //    v6----- v5
  //   /|      /|
  //  v1------v0|
  //  | |     | |
  //  | |v7---|-|v4
  //  |/      |/
  //  v2------v3
  // Coordinates
  var vertices = new Float32Array([
     2.0, 2.0, 2.0,  -2.0, 2.0, 2.0,  -2.0,-2.0, 2.0,   2.0,-2.0, 2.0, // v0-v1-v2-v3 front
     2.0, 2.0, 2.0,   2.0,-2.0, 2.0,   2.0,-2.0,-2.0,   2.0, 2.0,-2.0, // v0-v3-v4-v5 right
     2.0, 2.0, 2.0,   2.0, 2.0,-2.0,  -2.0, 2.0,-2.0,  -2.0, 2.0, 2.0, // v0-v5-v6-v1 up
    -2.0, 2.0, 2.0,  -2.0, 2.0,-2.0,  -2.0,-2.0,-2.0,  -2.0,-2.0, 2.0, // v1-v6-v7-v2 left
    -2.0,-2.0,-2.0,   2.0,-2.0,-2.0,   2.0,-2.0, 2.0,  -2.0,-2.0, 2.0, // v7-v4-v3-v2 down
     2.0,-2.0,-2.0,  -2.0,-2.0,-2.0,  -2.0, 2.0,-2.0,   2.0, 2.0,-2.0  // v4-v7-v6-v5 back
  ]);

  // Colors
  var colors = new Float32Array([
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v1-v2-v3 front
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v3-v4-v5 right
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v5-v6-v1 up
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v1-v6-v7-v2 left
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v7-v4-v3-v2 down
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0　    // v4-v7-v6-v5 back
 ]);

  // Normal
  var normals = new Float32Array([
    0.0, 0.0, 1.0,   0.0, 0.0, 1.0,   0.0, 0.0, 1.0,   0.0, 0.0, 1.0,  // v0-v1-v2-v3 front
    1.0, 0.0, 0.0,   1.0, 0.0, 0.0,   1.0, 0.0, 0.0,   1.0, 0.0, 0.0,  // v0-v3-v4-v5 right
    0.0, 1.0, 0.0,   0.0, 1.0, 0.0,   0.0, 1.0, 0.0,   0.0, 1.0, 0.0,  // v0-v5-v6-v1 up
   -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  // v1-v6-v7-v2 left
    0.0,-1.0, 0.0,   0.0,-1.0, 0.0,   0.0,-1.0, 0.0,   0.0,-1.0, 0.0,  // v7-v4-v3-v2 down
    0.0, 0.0,-1.0,   0.0, 0.0,-1.0,   0.0, 0.0,-1.0,   0.0, 0.0,-1.0   // v4-v7-v6-v5 back
  ]);

  // Indices of the vertices
  var indices = new Uint8Array([
     0, 1, 2,   0, 2, 3,    // front
     4, 5, 6,   4, 6, 7,    // right
     8, 9,10,   8,10,11,    // up
    12,13,14,  12,14,15,    // left
    16,17,18,  16,18,19,    // down
    20,21,22,  20,22,23     // back
 ]);

  // Write the vertex property to buffers (coordinates, colors and normals)
  if (!initArrayBuffer(gl, 'a_Position', vertices, 3, gl.FLOAT)) return -1;
  if (!initArrayBuffer(gl, 'a_Color', colors, 3, gl.FLOAT)) return -1;
  if (!initArrayBuffer(gl, 'a_Normal', normals, 3, gl.FLOAT)) return -1;

  // Unbind the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, null);

  // Write the indices to the buffer object
  var indexBuffer = gl.createBuffer();
  if (!indexBuffer) {
    console.log('Failed to create the buffer object');
    return false;
  }
  gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer);
  gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW);

  return indices.length;
}

function initArrayBuffer(gl, attribute, data, num, type) {
  // Create a buffer object
  var buffer = gl.createBuffer();
  if (!buffer) {
    console.log('Failed to create the buffer object');
    return false;
  }
  // Write date into the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
  gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);
  // Assign the buffer object to the attribute variable
  var a_attribute = gl.getAttribLocation(gl.program, attribute);
  if (a_attribute < 0) {
    console.log('Failed to get the storage location of ' + attribute);
    return false;
  }
  gl.vertexAttribPointer(a_attribute, num, type, false, 0, 0);
  // Enable the assignment of the buffer object to the attribute variable
  gl.enableVertexAttribArray(a_attribute);

  return true;
}

最关键的变化发生在顶点着色器中。首先使用模型矩阵变换顶点坐标，获得顶点在世界坐标系中的坐标(即变换后的坐标)，以便计算点光源光在顶点处的方向。点光源向四周放射光线，所以顶点处的光线方向是由点光源光坐标减去顶点坐标而得到的矢量。点光源在世界坐标系中的坐标已经传给了着色器中的u_LightPosition，而前面也已经算出了顶点在世界坐标系中的坐标，这样就计算出了光线方向矢量lightDirection。注意，需要使用normalize()函数进行归一化，以保证光线方向矢量的长度为1.0。最后，计算光线方向矢量与法向量的点积，从而算出每个顶点的颜色。

运行程序，你会发现效果更加逼真了。但是，如果仔细观察还是能发现一个问题:立方体表面上有不自然的线条，如图8.18所示。尝试运行PointLightedCube_animation(此例是动画，立方体在不停旋转)，你也许能看得更清楚。

出现该现象的原因在第5章讨论过的内插过程中提到过。你应该还记得，WebGL系统会根据顶点的颜色，内插出表面上每个片元的颜色。实际上，点光源光照射到一个表面上，所产生的效果(即每个片元获得的颜色)与简单使用4个顶点颜色(虽然这4个顶点的颜色也是由点光源产生)内插出的效果并不完全相同(在某些极端情况下甚至很不一样)，所以为了使效果更加逼真，我们需要对表面的每一点(而不仅仅是4个顶点计算光照效果。如果使用一个球体，二者的差异可能会更明显，如图8.19所示。

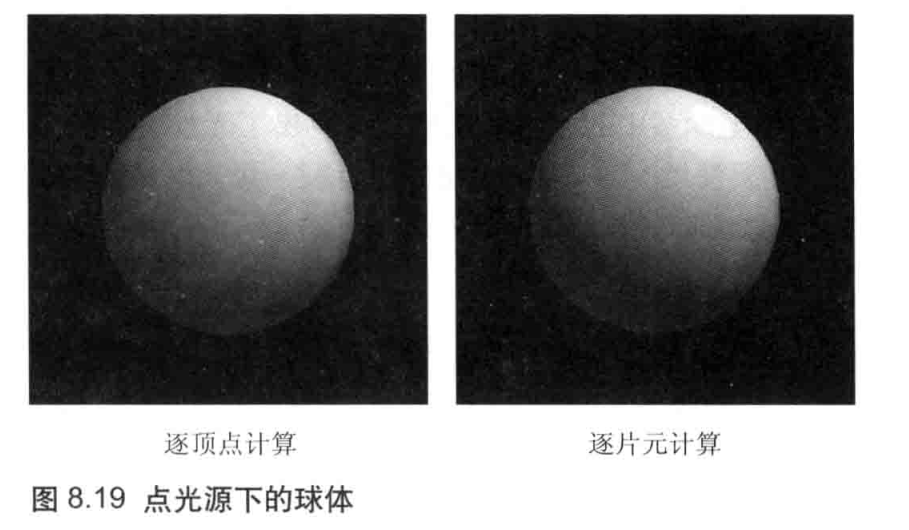
如你所见，左图中球体暗部与亮部的分界不是很自然，而右侧的就自然多了。如果你还是看不出来，可以在浏览器上运行程序进行观察。左图是PointLightedSphere，右图是PointLightedSphere_perFragment。

更逼真：逐片元光照

乍一听，要在表面的每一点上计算光照产生的颜色，似"乎是个不可能完成的任务。但实际上，我们只需要逐片元地进行计算。片元着色器总算要派上用场了。

示例程序是PointLightedCube_perFragment，效果如图8.20所示。

// PointLightedCube_perFragment.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'attribute vec4 a_Normal;\n' +
  'uniform mat4 u_MvpMatrix;\n' +
  'uniform mat4 u_ModelMatrix;\n' +    // 模型矩阵
  'uniform mat4 u_NormalMatrix;\n' +   // 用来变换法向量的矩阵
  'varying vec4 v_Color;\n' +
  'varying vec3 v_Normal;\n' +
  'varying vec3 v_Position;\n' +
  'void main() {\n' +
  '  gl_Position = u_MvpMatrix * a_Position;\n' +
     // 计算顶点的世界坐标
  '  v_Position = vec3(u_ModelMatrix * a_Position);\n' +
  '  v_Normal = normalize(vec3(u_NormalMatrix * a_Normal));\n' +
  '  v_Color = a_Color;\n' + 
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'uniform vec3 u_LightColor;\n' +     // 光的颜色
  'uniform vec3 u_LightPosition;\n' +  // 光源位置
  'uniform vec3 u_AmbientLight;\n' +   // 环境光颜色
  'varying vec3 v_Normal;\n' +
  'varying vec3 v_Position;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
     // 对法线进行归一化，因为其内插之后长度不一定是1.0
  '  vec3 normal = normalize(v_Normal);\n' +
     // 计算光线方向并归一化
  '  vec3 lightDirection = normalize(u_LightPosition - v_Position);\n' +
     // 计算光线方向和法向量的点积
  '  float nDotL = max(dot(lightDirection, normal), 0.0);\n' +
     // 计算 diffuse  ambient 以及最终的颜色
  '  vec3 diffuse = u_LightColor * v_Color.rgb * nDotL;\n' +
  '  vec3 ambient = u_AmbientLight * v_Color.rgb;\n' +
  '  gl_FragColor = vec4(diffuse + ambient, v_Color.a);\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // 
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Set the clear color and enable the depth test
  gl.clearColor(0.0, 0.0, 0.0, 1.0);
  gl.enable(gl.DEPTH_TEST);

  // Get the storage locations of uniform variables
  var u_ModelMatrix = gl.getUniformLocation(gl.program, 'u_ModelMatrix');
  var u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
  var u_NormalMatrix = gl.getUniformLocation(gl.program, 'u_NormalMatrix');
  var u_LightColor = gl.getUniformLocation(gl.program, 'u_LightColor');
  var u_LightPosition = gl.getUniformLocation(gl.program, 'u_LightPosition');
  var u_AmbientLight = gl.getUniformLocation(gl.program, 'u_AmbientLight');
  if (!u_ModelMatrix || !u_MvpMatrix || !u_NormalMatrix || !u_LightColor || !u_LightPosition　|| !u_AmbientLight) { 
    console.log('Failed to get the storage location');
    return;
  }

  // Set the light color (white)
  gl.uniform3f(u_LightColor, 1.0, 1.0, 1.0);
  // Set the light direction (in the world coordinate)
  gl.uniform3f(u_LightPosition, 2.3, 4.0, 3.5);
  // Set the ambient light
  gl.uniform3f(u_AmbientLight, 0.2, 0.2, 0.2);

  var modelMatrix = new Matrix4();  // Model matrix
  var mvpMatrix = new Matrix4();    // Model view projection matrix
  var normalMatrix = new Matrix4(); // Transformation matrix for normals

  // Calculate the model matrix
  modelMatrix.setRotate(90, 0, 1, 0); // Rotate around the y-axis
  // Calculate the view projection matrix
  mvpMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);
  mvpMatrix.lookAt(6, 6, 14, 0, 0, 0, 0, 1, 0);
  mvpMatrix.multiply(modelMatrix);
  // Calculate the matrix to transform the normal based on the model matrix
  normalMatrix.setInverseOf(modelMatrix);
  normalMatrix.transpose();

  // Pass the model matrix to u_ModelMatrix
  gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements);

  // Pass the model view projection matrix to u_mvpMatrix
  gl.uniformMatrix4fv(u_MvpMatrix, false, mvpMatrix.elements);

  // Pass the transformation matrix for normals to u_NormalMatrix
  gl.uniformMatrix4fv(u_NormalMatrix, false, normalMatrix.elements);

  // Clear color and depth buffer
  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

  // Draw the cube
  gl.drawElements(gl.TRIANGLES, n, gl.UNSIGNED_BYTE, 0);
}

function initVertexBuffers(gl) {
  // Create a cube
  //    v6----- v5
  //   /|      /|
  //  v1------v0|
  //  | |     | |
  //  | |v7---|-|v4
  //  |/      |/
  //  v2------v3
  // Coordinates
  var vertices = new Float32Array([
     2.0, 2.0, 2.0,  -2.0, 2.0, 2.0,  -2.0,-2.0, 2.0,   2.0,-2.0, 2.0, // v0-v1-v2-v3 front
     2.0, 2.0, 2.0,   2.0,-2.0, 2.0,   2.0,-2.0,-2.0,   2.0, 2.0,-2.0, // v0-v3-v4-v5 right
     2.0, 2.0, 2.0,   2.0, 2.0,-2.0,  -2.0, 2.0,-2.0,  -2.0, 2.0, 2.0, // v0-v5-v6-v1 up
    -2.0, 2.0, 2.0,  -2.0, 2.0,-2.0,  -2.0,-2.0,-2.0,  -2.0,-2.0, 2.0, // v1-v6-v7-v2 left
    -2.0,-2.0,-2.0,   2.0,-2.0,-2.0,   2.0,-2.0, 2.0,  -2.0,-2.0, 2.0, // v7-v4-v3-v2 down
     2.0,-2.0,-2.0,  -2.0,-2.0,-2.0,  -2.0, 2.0,-2.0,   2.0, 2.0,-2.0  // v4-v7-v6-v5 back
  ]);

  // Colors
  var colors = new Float32Array([
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v1-v2-v3 front
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v3-v4-v5 right
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v5-v6-v1 up
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v1-v6-v7-v2 left
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v7-v4-v3-v2 down
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0　    // v4-v7-v6-v5 back
 ]);

  // Normal
  var normals = new Float32Array([
    0.0, 0.0, 1.0,   0.0, 0.0, 1.0,   0.0, 0.0, 1.0,   0.0, 0.0, 1.0,  // v0-v1-v2-v3 front
    1.0, 0.0, 0.0,   1.0, 0.0, 0.0,   1.0, 0.0, 0.0,   1.0, 0.0, 0.0,  // v0-v3-v4-v5 right
    0.0, 1.0, 0.0,   0.0, 1.0, 0.0,   0.0, 1.0, 0.0,   0.0, 1.0, 0.0,  // v0-v5-v6-v1 up
   -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  // v1-v6-v7-v2 left
    0.0,-1.0, 0.0,   0.0,-1.0, 0.0,   0.0,-1.0, 0.0,   0.0,-1.0, 0.0,  // v7-v4-v3-v2 down
    0.0, 0.0,-1.0,   0.0, 0.0,-1.0,   0.0, 0.0,-1.0,   0.0, 0.0,-1.0   // v4-v7-v6-v5 back
  ]);

  // Indices of the vertices
  var indices = new Uint8Array([
     0, 1, 2,   0, 2, 3,    // front
     4, 5, 6,   4, 6, 7,    // right
     8, 9,10,   8,10,11,    // up
    12,13,14,  12,14,15,    // left
    16,17,18,  16,18,19,    // down
    20,21,22,  20,22,23     // back
 ]);

  // Write the vertex property to buffers (coordinates, colors and normals)
  if (!initArrayBuffer(gl, 'a_Position', vertices, 3)) return -1;
  if (!initArrayBuffer(gl, 'a_Color', colors, 3)) return -1;
  if (!initArrayBuffer(gl, 'a_Normal', normals, 3)) return -1;

  // Unbind the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, null);

  // Write the indices to the buffer object
  var indexBuffer = gl.createBuffer();
  if (!indexBuffer) {
    console.log('Failed to create the buffer object');
    return false;
  }
  gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer);
  gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW);

  return indices.length;
}

function initArrayBuffer(gl, attribute, data, num) {
  // Create a buffer object
  var buffer = gl.createBuffer();
  if (!buffer) {
    console.log('Failed to create the buffer object');
    return false;
  }
  // Write date into the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
  gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);
  // Assign the buffer object to the attribute variable
  var a_attribute = gl.getAttribLocation(gl.program, attribute);
  if (a_attribute < 0) {
    console.log('Failed to get the storage location of ' + attribute);
    return false;
  }
  gl.vertexAttribPointer(a_attribute, num, gl.FLOAT, false, 0, 0);
  // Enable the assignment of the buffer object to the attribute variable
  gl.enableVertexAttribArray(a_attribute);

  return true;
}

为了逐片元地计算光照，你需要知道:(1)片元在世界坐标系下的坐标，(2)片元处表面的法向量。

可以在顶点着色器中，将顶点的世界坐标和法向量以 varying 变量的形式传入片元着色器，片元着色器中的同名变量就已经是内插后的逐片元值了。

顶点着色器使用模型矩阵乘以顶点坐标计算出顶点的世界坐标，将其赋值给v_Position 变量。经过内插过程后,片元着色器就获得了逐片元的v_Position 变量，也就是片元的世界坐标。类似地，顶点着色器将顶点的法向量赋值给v_Normal变量，经过内插，片元着色器就获得了逐片元的 v Normal 变量，即片元的法向量。

片元着色器计算光照效果的方法与PointLightedCube.js相同。首先对法向量v_Norma1进行归一化，因为内插之后法向量可能不再是1.0了;然后，计算片元处的光线方向并对其归一化；接着计算法向量与光线方向的点积；最后分别计算点光源光和环境光产生的反射光颜色，并将两个结果加起来，赋值给gl_FragColor，片元就会显示为这个颜色。

如果场景中有超过一个点光源，那么就需要在片元着色器中计算每一个点光源(当然还有环境光)对片元的颜色贡献，并将它们全部加起来。换句话说，有几个点光源，就得按照式8.3计算几次。

层次模型

多个简单模型组成的复杂模型

我们已经知道如何平移、旋转简单的模型，比如二维的三角形或三维的立方体。但是实际用到的很多三维模型，如3D 游戏中的人物角色模型等，都是由多个较为简单的小模型(部件)组成。比如，图 9.1 显示了一个机器人手臂，这个模型就是由多个小的立方体模型组成的。在浏览器中运行示例程序 MultijointModel，然后尝试按下各个方向键和x、z、c、v键，看看有什么效果。

绘制由多个小部件组成的复杂模型，最关键的问题是如何处理模型的整体移动，以及各个小部件间的相对移动。

首先，考虑一下人类的手壁 :从肩部到指尖，包括上臂 (肘以上)、前臂 (肘以下)、手掌和手指，如图 9.2 所示

手臂的每个部分可以围绕关节运动，如图 9.2 所示

上臂可以绕肩关节旋转运动，并带动前臂、手掌和手指一起运动。

前臂可以绕肘关节运动，并带动手掌和手指一起运动，但不影响上臂。

手掌绕腕关节运动，并带动手指一起运动，但不影响上臂和前臂。

手指运动不影响上臂、前臂和手掌。

总之，当手臂的某个部位运动时，位于该部位以下的其他部位会随之一起运动，而位于该部位以上的其他部位不受影响。此外，这里的所有运动，都是围绕某个关节(肩关节、肘关节、腕关节、指关节)的转动。

层次结构模型

绘制机器人手臂这样一个复杂的模型，最常用的方法就是按照模型中各个部件的层次顺序，从高到低逐一绘制，并在每个关节上应用模型矩阵。比如，在图 9.2 中，肩关节、肘关节、腕关节，指关节都有各自的旋转矩阵。

注意，三维模型和现实中的人类或机器人不一样，它的部件并没有真正连接在一起。如果直接转动上臂，那么肘部以下的部分，包括前臂、手掌和手指，只会留在原地，这样手臂就断开了。所以，当上臂绕肩关节转动时，你需要在代码中实现“肘部以下部分跟随上臂转动”的逻辑。具体地，上臂绕肩关节转动了多少度，肘部以下的部分也应该绕肩关节转动多少度。

当情况较为简单时，实现“部件 A 转动带动部件 B 转动”可以很直接，只要对部件B 也施以部件 A 的旋转矩阵即可。比如，使用模型矩阵使上臂绕肩关节转动 30 度，然后在绘制肘关节以下的各部位时，为它们施加同一个模型矩阵，也令其绕肩关节转动 30度，如图 9.3 所示。这样，肘关节以下的部分就能自动跟随上臂转动了。

如果情况更复杂一些，比如先使上臂绕肩关节转动 30 度，然后使前臂绕肘关节转动10 度,那么对肘关节以下的部分,你就得先施加上臂绕肩关节转动30 度的矩阵(可称为“肩关节模型矩阵”)，然后再施加前臂绕肘关节转动 10 度的矩阵。将这两个矩阵相乘，其结果可称为“肘关节模型矩阵”,那么在绘制肘关节以下部分的时候,直接应用这个所谓的“肘关节模型矩阵”(而不考虑肩关节，因为肩关节的转动信息已经包含在该矩阵中了)作为模型矩阵就可以了。

按照上述方式编程，三维场景中的肩关节就能影响肘关节，使得上臂的运动带动前臂的运动，反过来，不管前臂如何运动都不会影响上臂。这就与现实中的情况相符合了

现在，你已经对这种由多个小模型组成的复杂模型的运动规律有了一些了解，下面来看一下示例程序。

单关节模型

先来看一个单关节模型的例子。示例程序 jointModel 绘制了一个仅由两个立方体部件组成的机器人手臂，其运行结果如图 9.4 (左)所示，手臂的两个部件为 arm1 与arm2，arm2 接在 arm1 的上面，如图 9.4(右)所示。你可以把 arm1想象成上臂，而把arm2 想象成前臂，而肩关节在最下面 (上臂在下而前臂在上，是为了以后加人手掌和手指后看得更清楚)。

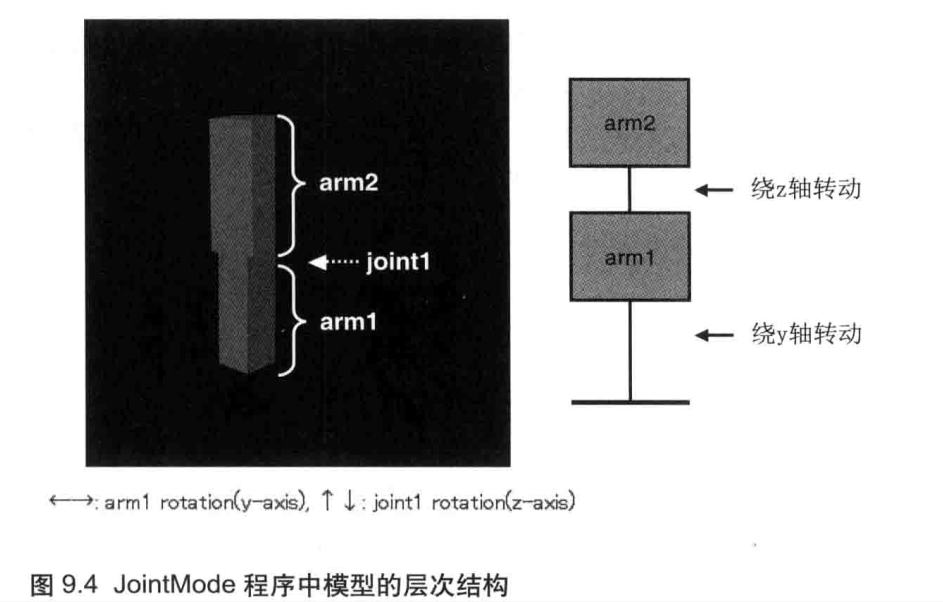
运行程序，用户可以使用左右方向键控制 arml (同时带动整条手臂)水平转动，使用上下方向键控制 arm2 绕joint1 关节垂直转动。比如，先按下方向键，arm2 逐渐向前倾斜 (图 9.5 左)，然后按右方向键，arm1 向右旋转 (图 9.5 右)。

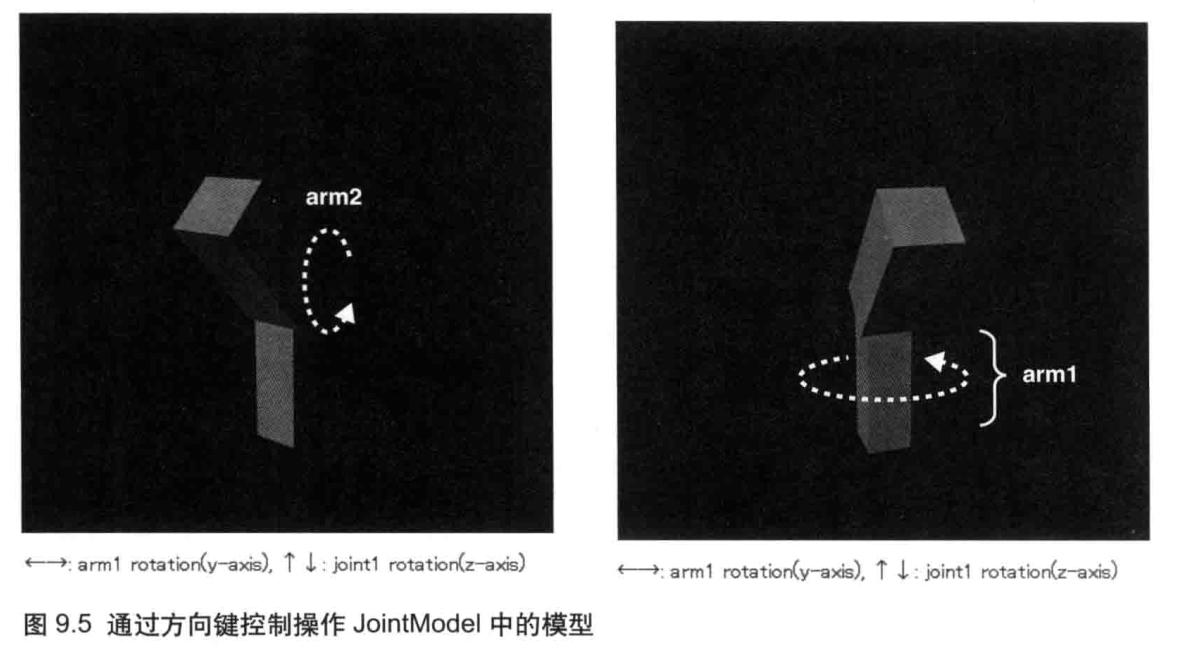
如你所见,arm2绕jointl 的转动并不影响 arml,而arml 的转动会带动arm2一起转动。

// JointModel.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Normal;\n' +
  'uniform mat4 u_MvpMatrix;\n' +
  'uniform mat4 u_NormalMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_MvpMatrix * a_Position;\n' +
  // 光照计算，使场景更加逼真
  '  vec3 lightDirection = normalize(vec3(0.0, 0.5, 0.7));\n' + // Light direction
  '  vec4 color = vec4(1.0, 0.4, 0.0, 1.0);\n' +
  '  vec3 normal = normalize((u_NormalMatrix * a_Normal).xyz);\n' +
  '  float nDotL = max(dot(normal, lightDirection), 0.0);\n' +
  '  v_Color = vec4(color.rgb * nDotL + vec3(0.1), color.a);\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex information
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Set the clear color and enable the depth test
  gl.clearColor(0.0, 0.0, 0.0, 1.0);
  gl.enable(gl.DEPTH_TEST);

  // Get the storage locations of uniform variables
  var u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
  var u_NormalMatrix = gl.getUniformLocation(gl.program, 'u_NormalMatrix');
  if (!u_MvpMatrix || !u_NormalMatrix) {
    console.log('Failed to get the storage location');
    return;
  }

  // Calculate the view projection matrix
  var viewProjMatrix = new Matrix4();
  viewProjMatrix.setPerspective(50.0, canvas.width / canvas.height, 1.0, 100.0);
  viewProjMatrix.lookAt(20.0, 10.0, 30.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);

  // 注册键盘事件响应函数
  document.onkeydown = function(ev){ keydown(ev, gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix); };

  draw(gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix);  // Draw the robot arm
}

var ANGLE_STEP = 3.0;    // 每次按键转动的角度
var g_arm1Angle = -90.0; // arm1的当前角度
var g_joint1Angle = 0.0; // joint1的当前角度（即arm2的角度）

function keydown(ev, gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix) {
  switch (ev.keyCode) {
    case 38: // 上方向键 -> joint1绕Z轴正向转动
      if (g_joint1Angle < 135.0) g_joint1Angle += ANGLE_STEP;
      break;
    case 40: // 下方向键 -> joint1绕Z轴负向转动
      if (g_joint1Angle > -135.0) g_joint1Angle -= ANGLE_STEP;
      break;
    case 39: // 右方向键 -> arm1绕y轴正向转动
      g_arm1Angle = (g_arm1Angle + ANGLE_STEP) % 360;
      break;
    case 37: // 左方向键 -> arm1绕y轴负向转动
      g_arm1Angle = (g_arm1Angle - ANGLE_STEP) % 360;
      break;
    default: return; // Skip drawing at no effective action
  }
  // 绘制手臂
  draw(gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix);
}

function initVertexBuffers(gl) {
  // Vertex coordinates（a cuboid 3.0 in width, 10.0 in height, and 3.0 in length with its origin at the center of its bottom)
  var vertices = new Float32Array([
    1.5, 10.0, 1.5, -1.5, 10.0, 1.5, -1.5,  0.0, 1.5,  1.5,  0.0, 1.5, // v0-v1-v2-v3 front
    1.5, 10.0, 1.5,  1.5,  0.0, 1.5,  1.5,  0.0,-1.5,  1.5, 10.0,-1.5, // v0-v3-v4-v5 right
    1.5, 10.0, 1.5,  1.5, 10.0,-1.5, -1.5, 10.0,-1.5, -1.5, 10.0, 1.5, // v0-v5-v6-v1 up
   -1.5, 10.0, 1.5, -1.5, 10.0,-1.5, -1.5,  0.0,-1.5, -1.5,  0.0, 1.5, // v1-v6-v7-v2 left
   -1.5,  0.0,-1.5,  1.5,  0.0,-1.5,  1.5,  0.0, 1.5, -1.5,  0.0, 1.5, // v7-v4-v3-v2 down
    1.5,  0.0,-1.5, -1.5,  0.0,-1.5, -1.5, 10.0,-1.5,  1.5, 10.0,-1.5  // v4-v7-v6-v5 back
  ]);

  // Normal
  var normals = new Float32Array([
    0.0, 0.0, 1.0,  0.0, 0.0, 1.0,  0.0, 0.0, 1.0,  0.0, 0.0, 1.0, // v0-v1-v2-v3 front
    1.0, 0.0, 0.0,  1.0, 0.0, 0.0,  1.0, 0.0, 0.0,  1.0, 0.0, 0.0, // v0-v3-v4-v5 right
    0.0, 1.0, 0.0,  0.0, 1.0, 0.0,  0.0, 1.0, 0.0,  0.0, 1.0, 0.0, // v0-v5-v6-v1 up
   -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, // v1-v6-v7-v2 left
    0.0,-1.0, 0.0,  0.0,-1.0, 0.0,  0.0,-1.0, 0.0,  0.0,-1.0, 0.0, // v7-v4-v3-v2 down
    0.0, 0.0,-1.0,  0.0, 0.0,-1.0,  0.0, 0.0,-1.0,  0.0, 0.0,-1.0  // v4-v7-v6-v5 back
  ]);

  // Indices of the vertices
  var indices = new Uint8Array([
     0, 1, 2,   0, 2, 3,    // front
     4, 5, 6,   4, 6, 7,    // right
     8, 9,10,   8,10,11,    // up
    12,13,14,  12,14,15,    // left
    16,17,18,  16,18,19,    // down
    20,21,22,  20,22,23     // back
  ]);

  // Write the vertex property to buffers (coordinates and normals)
  if (!initArrayBuffer(gl, 'a_Position', vertices, gl.FLOAT, 3)) return -1;
  if (!initArrayBuffer(gl, 'a_Normal', normals, gl.FLOAT, 3)) return -1;

  // Unbind the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, null);

  // Write the indices to the buffer object
  var indexBuffer = gl.createBuffer();
  if (!indexBuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }
  gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer);
  gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW);

  return indices.length;
}

function initArrayBuffer(gl, attribute, data, type, num) {
  // Create a buffer object
  var buffer = gl.createBuffer();
  if (!buffer) {
    console.log('Failed to create the buffer object');
    return false;
  }
  // Write date into the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
  gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);

  // Assign the buffer object to the attribute variable
  var a_attribute = gl.getAttribLocation(gl.program, attribute);
  if (a_attribute < 0) {
    console.log('Failed to get the storage location of ' + attribute);
    return false;
  }
  gl.vertexAttribPointer(a_attribute, num, type, false, 0, 0);
  // Enable the assignment of the buffer object to the attribute variable
  gl.enableVertexAttribArray(a_attribute);

  return true;
}

// 坐标变换矩阵
var g_modelMatrix = new Matrix4(), g_mvpMatrix = new Matrix4();

function draw(gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix) {
  // Clear color and depth buffer
  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

  // Arm1
  var arm1Length = 10.0; // arm1的长度
  g_modelMatrix.setTranslate(0.0, -12.0, 0.0);
  g_modelMatrix.rotate(g_arm1Angle, 0.0, 1.0, 0.0);    // 绕y轴旋转
  drawBox(gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix); // 绘制

  // Arm2
  g_modelMatrix.translate(0.0, arm1Length, 0.0); 　　　// 移至joint1处
  g_modelMatrix.rotate(g_joint1Angle, 0.0, 0.0, 1.0);  // 绕z轴旋转
  g_modelMatrix.scale(1.3, 1.0, 1.3); // 使立方体粗一点
  drawBox(gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix); // 绘制
}

var g_normalMatrix = new Matrix4(); // 法线的旋转矩阵

// 绘制立方体
function drawBox(gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix) {
  // 计算模型视图矩阵并传给u_MvpMatrix变量
  g_mvpMatrix.set(viewProjMatrix);
  g_mvpMatrix.multiply(g_modelMatrix);
  gl.uniformMatrix4fv(u_MvpMatrix, false, g_mvpMatrix.elements);
  // 计算法线变换矩阵并传给u_normalMatrix变量
  g_normalMatrix.setInverseOf(g_modelMatrix);
  g_normalMatrix.transpose();
  gl.uniformMatrix4fv(u_NormalMatrix, false, g_normalMatrix.elements);
  // 绘制
  gl.drawElements(gl.TRIANGLES, n, gl.UNSIGNED_BYTE, 0);
}

和以前的程序相比，main() 函数基本没有变化，主要的变化发生在initVertexBuffers()函数中,它将 arml和arm2 的数据写人了相应的缓冲区以前程序中的立方体都是以原点为中心，且边长为2.0，本例为了更好地模拟机器人手臂，使用如图 9.6 所示的立方体，原点位于底面中心，底面是边长为3.0的正方形，高度为 10.0。将原点置于立方体的底面中心，是为了便于使立方体绕关节转动 (比如，肘关节就位于前臂立方体的底面中心)，如图9.5 所示。arm1和 arm2 都使用这个立方体。

绘制层次模型（draw()）

如你所见，draw() 函数内部调用了 drawBox()函数，每调用一次绘制一个部件，先绘制下方较细 arm1，再绘制上方较粗 arm2。

绘制单个部件的步骤是 :(1)调用 setTranslate()或 translate() 进行平移 ;(2)调用 rotate() 进行旋转;(3) 调用 drawBox() 进行绘制。

绘制整个模型时，需要按照各部件的层次顺序，先 arm1 后 arm2，再执行 (1)平移，(2) 旋转，(3) 绘制。

绘制 arml 的步骤如下:首先在模型矩阵g_modelMatrix上调用 setTranslate()函数,使之平移(0.0,-12.0,0.0) 到稍下方位置 ;然后调用 rotate() 函数，绕y轴旋转 g armlAngle 角度；最后调用 drawBox()函数绘制 arm1。

接着来绘制 arm2，它与 arm1 在jointl 处连接，如图 9.7 所示，我们应当从该处上开始绘制 arm2。但是此时，模型矩阵还是处于绘制 arml 的状态(向下平移并绕y轴旋转下,所以得先调用 translate()函数沿y轴向上平移 arml的高度armlLength。注意这里调用的是 translate() 而不是 setTranslate0)，因为这次平移是在之前的基础上进行的。

然后,使用 g_joint1Angle进行肘关节处的转动,并在x和z轴稍作拉伸，使前臂看上去粗一些，以便与上臂区分开。

这样一来，每当 keydown 函数更新了g_joint1Angle 变量和 g_armlAngle 变量的值，然后调用 draw() 函数进行绘制时，就能绘制出最新状态的机器人手臂，arm1 的位置取决于g_armlAngle 变量，而arm2 的位置取决于g_jointAngle 变量(当然也受garmlAngle 的影响)。

drawBox()函数的任务是绘制机器人手臂的某一个立方体部件，如上臂或前臂。它首先计算模型视图投影矩阵，传递给u MvpMatrix变量，然后根据模型矩阵计算法向量变换矩阵，传递给u_NormalMatrix变量，最后绘制立方体。

绘制层次模型的基本流程就是这样了。虽然本例只有两个立方体和一个连接关节但是绘制更加复杂的模型，其原理与本节是一致的，要做的只是重复上述步骤而已。

显然，上面这个例子中的机器人手臂与真正的人类手臂比起来，只是一个骨架。要模拟现实中的人类手臂，应该对皮肤进行建模，而这个话题已经超越了本书的讨论范围关于皮肤建模，可以参考 OpenGL ES2.0 Programming Guide 一书。

多节点模型

这一节将把 JointMode1 扩展为 MultiJointModel，后者绘制一个具有多个关节的完整的机器人手臂,包括基座(base)、上臂(arm1)、前臂(arm2)、手掌(palm)、两根手指(fngerl& fnger2)，全部可以通过键盘来控制。arml和 arm2 的连接关节jointl 位于 arml 顶部arm2 和 palm 的连接关节joint2 位于 arm2 顶部,fingerl 和 finger2 位于 palm一端,如图 9.8所示。

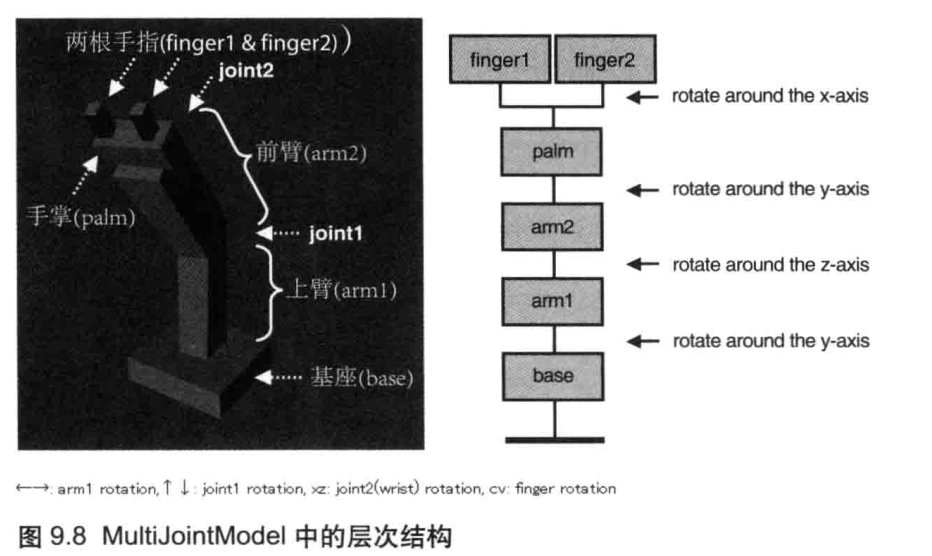
用户可以通过键盘操纵机器人手臂，arm1和 arm2 的操作和 JointModel一样，此外,还可以使用x和z键旋转joint2 (腕关节)，使用 C和V 键旋转 fngerl 和 fnger2。控制这些小部件旋转角度的全局变量，如图 9.9 所示。

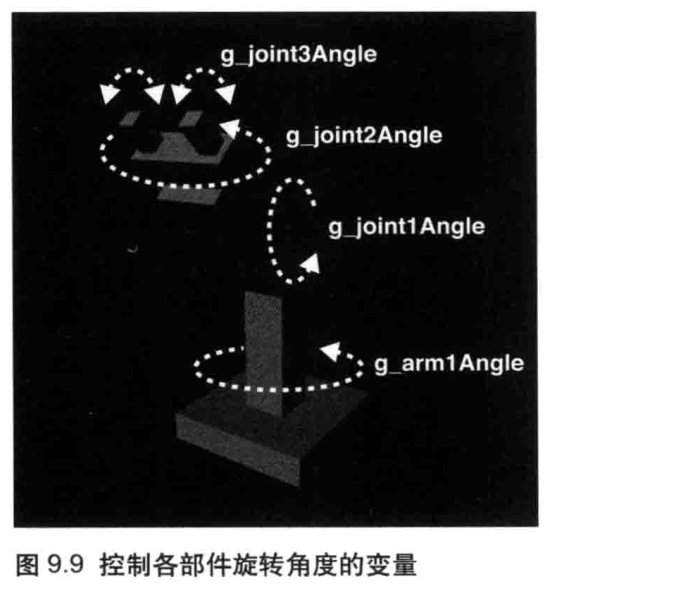
// MultiJointModel.js (c) 2012 matsuda and itami
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Normal;\n' +
  'uniform mat4 u_MvpMatrix;\n' +
  'uniform mat4 u_NormalMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_MvpMatrix * a_Position;\n' +
  // Shading calculation to make the arm look three-dimensional
  '  vec3 lightDirection = normalize(vec3(0.0, 0.5, 0.7));\n' + // Light direction
  '  vec4 color = vec4(1.0, 0.4, 0.0, 1.0);\n' +  // Robot color
  '  vec3 normal = normalize((u_NormalMatrix * a_Normal).xyz);\n' +
  '  float nDotL = max(dot(normal, lightDirection), 0.0);\n' +
  '  v_Color = vec4(color.rgb * nDotL + vec3(0.1), color.a);\n' +
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }

  // Set the vertex information
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Set the clear color and enable the depth test
  gl.clearColor(0.0, 0.0, 0.0, 1.0);
  gl.enable(gl.DEPTH_TEST);

  // Get the storage locations of uniform variables
  var u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
  var u_NormalMatrix = gl.getUniformLocation(gl.program, 'u_NormalMatrix');
  if (!u_MvpMatrix || !u_NormalMatrix) {
    console.log('Failed to get the storage location');
    return;
  }

  // Calculate the view projection matrix
  var viewProjMatrix = new Matrix4();
  viewProjMatrix.setPerspective(50.0, canvas.width / canvas.height, 1.0, 100.0);
  viewProjMatrix.lookAt(20.0, 10.0, 30.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0);

  // Register the event handler to be called on key press
  document.onkeydown = function(ev){ keydown(ev, gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix); };

　draw(gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix); // Draw the robot arm
}

var ANGLE_STEP = 3.0;     // The increments of rotation angle (degrees)
var g_arm1Angle = 90.0;   // The rotation angle of arm1 (degrees)
var g_joint1Angle = 45.0; // The rotation angle of joint1 (degrees)
var g_joint2Angle = 0.0;  // The rotation angle of joint2 (degrees)
var g_joint3Angle = 0.0;  // The rotation angle of joint3 (degrees)

function keydown(ev, gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix) {
  switch (ev.keyCode) {
    case 40: // Up arrow key -> the positive rotation of joint1 around the z-axis
      if (g_joint1Angle < 135.0) g_joint1Angle += ANGLE_STEP;
      break;
    case 38: // Down arrow key -> the negative rotation of joint1 around the z-axis
      if (g_joint1Angle > -135.0) g_joint1Angle -= ANGLE_STEP;
      break;
    case 39: // Right arrow key -> the positive rotation of arm1 around the y-axis
      g_arm1Angle = (g_arm1Angle + ANGLE_STEP) % 360;
      break;
    case 37: // Left arrow key -> the negative rotation of arm1 around the y-axis
      g_arm1Angle = (g_arm1Angle - ANGLE_STEP) % 360;
      break;
    case 90: // 'ｚ'key -> the positive rotation of joint2
      g_joint2Angle = (g_joint2Angle + ANGLE_STEP) % 360;
      break; 
    case 88: // 'x'key -> the negative rotation of joint2
      g_joint2Angle = (g_joint2Angle - ANGLE_STEP) % 360;
      break;
    case 86: // 'v'key -> the positive rotation of joint3
      if (g_joint3Angle < 60.0)  g_joint3Angle = (g_joint3Angle + ANGLE_STEP) % 360;
      break;
    case 67: // 'c'key -> the nagative rotation of joint3
      if (g_joint3Angle > -60.0) g_joint3Angle = (g_joint3Angle - ANGLE_STEP) % 360;
      break;
    default: return; // Skip drawing at no effective action
  }
  // Draw the robot arm
  draw(gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix);
}

function initVertexBuffers(gl) {
  // Coordinates（Cube which length of one side is 1 with the origin on the center of the bottom)
  var vertices = new Float32Array([
    0.5, 1.0, 0.5, -0.5, 1.0, 0.5, -0.5, 0.0, 0.5,  0.5, 0.0, 0.5, // v0-v1-v2-v3 front
    0.5, 1.0, 0.5,  0.5, 0.0, 0.5,  0.5, 0.0,-0.5,  0.5, 1.0,-0.5, // v0-v3-v4-v5 right
    0.5, 1.0, 0.5,  0.5, 1.0,-0.5, -0.5, 1.0,-0.5, -0.5, 1.0, 0.5, // v0-v5-v6-v1 up
   -0.5, 1.0, 0.5, -0.5, 1.0,-0.5, -0.5, 0.0,-0.5, -0.5, 0.0, 0.5, // v1-v6-v7-v2 left
   -0.5, 0.0,-0.5,  0.5, 0.0,-0.5,  0.5, 0.0, 0.5, -0.5, 0.0, 0.5, // v7-v4-v3-v2 down
    0.5, 0.0,-0.5, -0.5, 0.0,-0.5, -0.5, 1.0,-0.5,  0.5, 1.0,-0.5  // v4-v7-v6-v5 back
  ]);

  // Normal
  var normals = new Float32Array([
    0.0, 0.0, 1.0,  0.0, 0.0, 1.0,  0.0, 0.0, 1.0,  0.0, 0.0, 1.0, // v0-v1-v2-v3 front
    1.0, 0.0, 0.0,  1.0, 0.0, 0.0,  1.0, 0.0, 0.0,  1.0, 0.0, 0.0, // v0-v3-v4-v5 right
    0.0, 1.0, 0.0,  0.0, 1.0, 0.0,  0.0, 1.0, 0.0,  0.0, 1.0, 0.0, // v0-v5-v6-v1 up
   -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, -1.0, 0.0, 0.0, // v1-v6-v7-v2 left
    0.0,-1.0, 0.0,  0.0,-1.0, 0.0,  0.0,-1.0, 0.0,  0.0,-1.0, 0.0, // v7-v4-v3-v2 down
    0.0, 0.0,-1.0,  0.0, 0.0,-1.0,  0.0, 0.0,-1.0,  0.0, 0.0,-1.0  // v4-v7-v6-v5 back
  ]);

  // Indices of the vertices
  var indices = new Uint8Array([
     0, 1, 2,   0, 2, 3,    // front
     4, 5, 6,   4, 6, 7,    // right
     8, 9,10,   8,10,11,    // up
    12,13,14,  12,14,15,    // left
    16,17,18,  16,18,19,    // down
    20,21,22,  20,22,23     // back
  ]);

  // Write the vertex property to buffers (coordinates and normals)
  if (!initArrayBuffer(gl, 'a_Position', vertices, gl.FLOAT, 3)) return -1;
  if (!initArrayBuffer(gl, 'a_Normal', normals, gl.FLOAT, 3)) return -1;

  // Unbind the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, null);

  // Write the indices to the buffer object
  var indexBuffer = gl.createBuffer();
  if (!indexBuffer) {
    console.log('Failed to create the buffer object');
    return -1;
  }
  gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer);
  gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW);

  return indices.length;
}

function initArrayBuffer(gl, attribute, data, type, num) {
  // Create a buffer object
  var buffer = gl.createBuffer();
  if (!buffer) {
    console.log('Failed to create the buffer object');
    return false;
  }
  // Write date into the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
  gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);

  // Assign the buffer object to the attribute variable
  var a_attribute = gl.getAttribLocation(gl.program, attribute);
  if (a_attribute < 0) {
    console.log('Failed to get the storage location of ' + attribute);
    return false;
  }
  gl.vertexAttribPointer(a_attribute, num, type, false, 0, 0);
  // Enable the assignment of the buffer object to the attribute variable
  gl.enableVertexAttribArray(a_attribute);

  return true;
}

// Coordinate transformation matrix
var g_modelMatrix = new Matrix4(), g_mvpMatrix = new Matrix4();

function draw(gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix) {
  // Clear color and depth buffer
  gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

  // Draw a base
  var baseHeight = 2.0;
  g_modelMatrix.setTranslate(0.0, -12.0, 0.0);
  drawBox(gl, n, 10.0, baseHeight, 10.0, viewProjMatrix, u_MvpMatrix, u_NormalMatrix);
 
  // Arm1
  var arm1Length = 10.0;
  g_modelMatrix.translate(0.0, baseHeight, 0.0);     // Move onto the base
  g_modelMatrix.rotate(g_arm1Angle, 0.0, 1.0, 0.0);  // Rotate around the y-axis
  drawBox(gl, n, 3.0, arm1Length, 3.0, viewProjMatrix, u_MvpMatrix, u_NormalMatrix); // Draw

  // Arm2
  var arm2Length = 10.0;
  g_modelMatrix.translate(0.0, arm1Length, 0.0);       // Move to joint1
  g_modelMatrix.rotate(g_joint1Angle, 0.0, 0.0, 1.0);  // Rotate around the z-axis
  drawBox(gl, n, 4.0, arm2Length, 4.0, viewProjMatrix, u_MvpMatrix, u_NormalMatrix); // Draw

  // A palm
  var palmLength = 2.0;
  g_modelMatrix.translate(0.0, arm2Length, 0.0);       // Move to palm
  g_modelMatrix.rotate(g_joint2Angle, 0.0, 1.0, 0.0);  // Rotate around the y-axis
  drawBox(gl, n, 2.0, palmLength, 6.0, viewProjMatrix, u_MvpMatrix, u_NormalMatrix);  // Draw

  // Move to the center of the tip of the palm
  g_modelMatrix.translate(0.0, palmLength, 0.0);

  // Draw finger1
  pushMatrix(g_modelMatrix);
    g_modelMatrix.translate(0.0, 0.0, 2.0);
    g_modelMatrix.rotate(g_joint3Angle, 1.0, 0.0, 0.0);  // Rotate around the x-axis
    drawBox(gl, n, 1.0, 2.0, 1.0, viewProjMatrix, u_MvpMatrix, u_NormalMatrix);
  g_modelMatrix = popMatrix();

  // Draw finger2
  g_modelMatrix.translate(0.0, 0.0, -2.0);
  g_modelMatrix.rotate(-g_joint3Angle, 1.0, 0.0, 0.0);  // Rotate around the x-axis
  drawBox(gl, n, 1.0, 2.0, 1.0, viewProjMatrix, u_MvpMatrix, u_NormalMatrix);
}

var g_matrixStack = []; // Array for storing a matrix
function pushMatrix(m) { // Store the specified matrix to the array
  var m2 = new Matrix4(m);
  g_matrixStack.push(m2);
}

function popMatrix() { // Retrieve the matrix from the array
  return g_matrixStack.pop();
}

var g_normalMatrix = new Matrix4();  // Coordinate transformation matrix for normals

// Draw rectangular solid
function drawBox(gl, n, width, height, depth, viewProjMatrix, u_MvpMatrix, u_NormalMatrix) {
  pushMatrix(g_modelMatrix);   // Save the model matrix
    // Scale a cube and draw
    g_modelMatrix.scale(width, height, depth);
    // Calculate the model view project matrix and pass it to u_MvpMatrix
    g_mvpMatrix.set(viewProjMatrix);
    g_mvpMatrix.multiply(g_modelMatrix);
    gl.uniformMatrix4fv(u_MvpMatrix, false, g_mvpMatrix.elements);
    // Calculate the normal transformation matrix and pass it to u_NormalMatrix
    g_normalMatrix.setInverseOf(g_modelMatrix);
    g_normalMatrix.transpose();
    gl.uniformMatrix4fv(u_NormalMatrix, false, g_normalMatrix.elements);
    // Draw
    gl.drawElements(gl.TRIANGLES, n, gl.UNSIGNED_BYTE, 0);
  g_modelMatrix = popMatrix();   // Retrieve the model matrix
}

着色器和着色器程序对象：initShaders() 函数的作用

将研究一下以前一直使用的辅助函数 initshaders0)。以前的所有程序都使用了这个函数，它隐藏了建立和初始化着色器的细节。掌握这部分内容并不是必须的，直接使用 initshaders() 函数也能够编号出相当不错的 WebGL 程序，但如果你确实很想知道 WebGL 原生 API 是如何将字符串形式的 GLSL ES 代码编译为显卡中运行的着色器程序，那么这一节的内容将大大满足你的好奇心。

initshaders() 函数的作用是，编译 GLSL ES 代码，创建和初始化着色器供 WebGL 使用。具体地，分为以下 7个步骤 :

创建着色器对象(gl.createShader())

向着色器对象中填充着色器程序的源代码(gl.shaderSource ())。

编译着色器(gl.compileShader())。

创建程序对象(gl.createProgram())。

为程序对象分配着色器 (gl.attachShader())

连接程序对象(gl.linkProgram())。

使用程序对象(gl.useProgram())。

虽然每一步看上去都比较简单，但是放在一起显得复杂了，我们将逐条讨论。首先，你需要知道这里出现了两种对象:着色器对象(shader object)和程序对象 (program object).

着色器对象：着色器对象管理一个顶点着色器或一个片元着色器。每一个着色器都有一个着色器对象。

程序对象：程序对象是管理着色器对象的容器。WebGL 中，一个程序对象必须包含.个顶点着色器和一个片元着色器。

着色器对象和程序对象间的关系如图 9.10 所示。

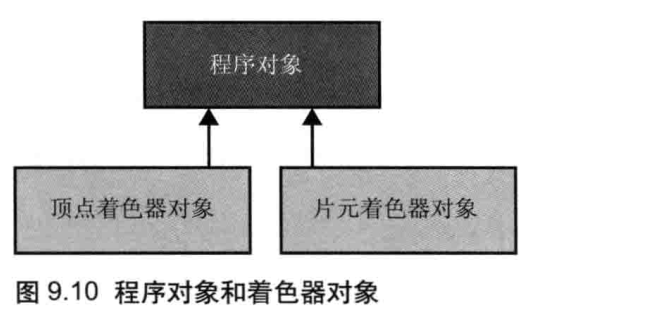
创建着色器对象（gl.createShader()）

所有的着色器对象都必须通过调用 gl.createShader()来创建。

createShader()函数根据传人的参数创建一个顶点着色器或者片元着色器。如果不再需要这个着色器，可以使用gl.deleteShader() 函数来删除着色器。

注意，如果着色器对象还在使用 (也就是说已经使用 gl.attachshader() 函数使之附加在了程序对象上，我们马上就会讨论该函数)，那么 gl.deleteShader() 并不会立刻删除着色器，而是要等到程序对象不再使用该着色器后，才将其删除

指定着色器对象的代码（gl.shaderSource()）

通过 gl.shaderSource() 函数向着色器指定 GLSL ES 源代码。

编译着色器（gl.compileShader()）

向着色器对象传人源代码之后，还需要对其进行编译才能够使用。GLSL ES 语言和 JavaScript 不同而更接近 C或 C++，在使用之前需要编译成二进制的可执行格式WebGL 系统真正使用的是这种可执行格式。使用 gl.compileShader() 函数进行编译。注意，如果你通过调用 gl.shaderSource()，用新的代码替换掉了着色器中旧的代码，WebGL 系统中的用旧的代码编译出的可执行部分不会被自动替换，你需要手动地重新进行编译

当调用 gl.compileShader() 函数时，如果着色器源代码中存在错误，那么就会出现编译错误。可以调用gl.getShaderParameter() 函数来检查着色器的状态。

调用 gl.getShaderParameter() 并将参数 pname 指定为 gl.COMPIIE STATUS，就可以检查着色器编译是否成功。

如果编译失败，gl.getShaderParameter()会返回 fals，webgl系统会把编译错误的具体内容写入着色器的信息日志（information log）,我们可以通过 gl.getShaderInfoLog()来获取

创建程序对象（gl.createProgram()）

如前所述，程序对象包含了顶点着色器和片元着色器，可以调用 gl.createProgram()来创建程序对象。事实上，之前使用程序对象，gl.getAttribLocation() 函数和gl.getUniformLocation() 函数的第1个参数，就是这个程序对象。

类似地，可以使用 gl.deleteProgram() 函数来删除程序对象

一旦程序对象被创建之后，需要向程序附上两个着色器

为程序对象分配着色器对象（gl.attachShader()）

WebGL 系统要运行起来，必须要有两个着色器:一个顶点着色器和一个片元着色器可以使用 gl.attachShader() 函数为程序对象分配这两个着色器。

着色器在附给程序对象前，并不一定要为其指定代码或进行编译 (也就是说，把空的着色器附给程序对象也是可以的)。

类似地，可以使用 gl.detachShader() 函数来解除分配给程序对象的着色器。

连接程序对象（gl.linkProgram()）

在为程序对象分配了两个着色器对象后，还需要将 (顶点着色器和片元)着色器连接起来。使用 gl.linkProgram() 函数来进行这一步操作。

程序对象进行着色器连接操作，目的是保证 :
(1)顶点着色器和片元着色器的varying 变量同名同类型，且一一对应;
(2)顶点着色器对每个 varying 变量赋了值;
(3)顶点着色器和片元着色器中的同名uniform变量也是同类型的(无需一一对应，即某些uniform变量可以出现在一个着色器中而不出现在另一个中);
(4)着色器中的 attribute变量、uniform 变量和 varying 变量的个数没有超过着色器的上限 (见表 6.14)，等等。

在着色器连接之后，应当检查是否连接成功。通过调用 gl.getProgramParameters()函数来实现。

如果程序已经成功连接,我们就得到了一个二进制的可执行模块供 WebGL 系统使用。如果连接失败了，也可以通过调用 gl.getProgramInfoLog() 从信息日志中获取连接出错信息。

告知WebGL 系统所使用的程序对象（gl.useProgram()）

最后，通过调用 gl.usePorgram() 告知 WebGL 系统绘制时使用哪个程序对象。

这个函数的存在使得 WebGL 具有了一个强大的特性，那就是在绘制前准备多个程序对象，然后在绘制的时候根据需要切换程序对象。

这样，建立和初始化着色器的任务就算完成了。如你所见，initshaders() 函数隐藏了大量的细节，我们可以放心地使用该函数来创建和初始化着色器，而不必考虑这些细节。本质上，在该函数顺利执行后，顶点着色器和片元着色器就已经就位了，只需要调用 gl.drawArrays() 或 gl.drawElements() 来使整个 WebGL 系统运行起来。

posted @ 2023-07-17 12:35 CD、小月阅读(115) 评论(0) 编辑收藏举报

刷新页面返回顶部

一纾

WebGL编程读书笔记

WebGL概述

WebGL起源

WebGL程序的结构

WebGL入门

最短的WebGL程序：清空绘图区

关于绘图上下文

设置<canvas>的背景色

清空<canvas>

绘制一个点（版本1）

着色器

使用着色器的WebGL 程序的结构

初始化着色器

顶点着色器

片元着色器

绘制操作

WebGL坐标系统

绘制一个点（版本2）

使用attribute 变量

获取attribute 变量的存储位置

向attribute 变量赋值

gl.vertexAttrib3f() 的同族函数

通过鼠标点击绘点

响应鼠标点击事件

改变点的颜色

uniform 变量

获取uniform 变量的存储地址

向uniform 变量赋值

gl.uniform4f() 的同族函数

绘制和变换三角形

绘制多个点

使用缓冲区对象

创建缓冲区对象（gl.createBuffer()）

绑定缓冲区（gl.bindBuffer()）

向缓冲区对象中写入数据（ gl.bufferData() ）

类型化数组

将缓冲区对象分配给attribute 变量（gl.vertexAttribPointer()）

开启attribute 变量（ gl.enableVertexAttribArray() ）

gl.drawArrays() 的第2 个和第3 个参数

Hello Triangle

基本图形

Hello Rectangle（HelloQuad）

移动、旋转和缩放

平移

旋转

变换矩阵：旋转

变换矩阵：平移

4x4的旋转矩阵

示例程序（RotatedTriangle_Matrix.js 旋转矩阵）

平移：相同的策略

变化矩阵：缩放

高级变换与动画基础

平移，然后旋转

矩阵变换库：cuon-matrix.js

复合变换

动画

请求再次被调用（requestAnimationFrame()）

颜色与纹理

将非坐标数据传入顶点着色器

gl.vertexAttribPointer() 的步进和偏移参数

修改颜色（varying 变量）

彩色三角形（ColoredTriangle.js）

几何形状的装配和光栅化

调用片元着色器

varying 变量的作用和内插过程

在矩形表面贴上图像

纹理坐标

将纹理图像粘贴到几何图形上

设置纹理坐标（initVertexBuffers()）

配置和加载纹理（ initTextures() ）

为WebGL 配置纹理（ loadTexture() ）

图像Y 轴反转

激活纹理单元（gl.activeTexture()）

绑定纹理对象（gl.bindTexture()）

配置纹理对象的参数（gl.texParameteri()）

将纹理图像分配给纹理对象（ gl.texImage2D() ）

将纹理单元传递给片元着色器（ gl.uniform1i() ）

从顶点着色器向片元着色器传输纹理坐标

在片元着色器中获取纹理像素颜色（ texture2D() ）