实验一 感知器及其应用

目录

• 一、作业信息
• 二、实验内容
• 三、实验小结

一、作业信息

|博客班级|机器学习实验-计算机18级 (安徽工程大学 - 计算机与信息学院)
|----|----|----|
|作业要求|1. 按实验内容撰写实验过程；2. 报告中涉及到的代码，每一行需要有详细的注释；3. 按自己的理解重新组织，禁止粘贴复制实验内容！|
|作业目的|1. 理解感知器算法原理，能实现感知器算法；2. 掌握机器学习算法的度量指标；3. 掌握最小二乘法进行参数估计基本原理；4. 针对特定应用场景及数据，能构建感知器模型并进行预测。|
| 学号| 3180701335|

二、实验内容

二分类模型
损失函数
算法
随即梯度下降法 Stochastic Gradient Descent
随机抽取一个误分类点使其梯度下降。
当实例点被误分类，即位于分离超平面的错误侧，则调整w, b的值，使分离超平面向该无分类点的一侧移动，直
至误分类点被正确分类
𝑓(𝑥) = 𝑠𝑖𝑔𝑛(𝑤 ∗ 𝑥 + 𝑏)
𝐿(𝑤, 𝑏) = −Σ𝑦𝑖(𝑤 ∗ 𝑥𝑖 + 𝑏)
𝑤 = 𝑤 + 𝜂𝑦𝑖𝑥𝑖
𝑏 = 𝑏 + 𝜂𝑦𝑖
拿出iris数据集中两个分类的数据和[sepal length，sepal width]作为特征
拿出iris数据集中两个分类的数据和[sepal length，sepal width]作为特征
In [1]:

import pandas as pd #调用pandas库
import numpy as np #调用numpy库
from sklearn.datasets import load_iris #加载数据集
import matplotlib.pyplot as plt #调用函数matplotlib.pyplot集合
%matplotlib inline #调用matplotlib.pyplot的绘图函数plot()进行绘图的时候，或者生成一个figure画布的时候，可以直接在python console里面生成图像

In[2]

#load data
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names) #同时DataFrame可以设置列名columns与行名index
df['label'] = iris.target# 表头字段就是key

In[3]

#
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']# 对其中的4个特征进行训练
df.label.value_counts()

In[4]

plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

In[5]

data = np.array(df.iloc[:100, [0, 1, -1]])#提取取前100条数据，为了方便展示，取2个特征

In[6]

X, y = data[:,:-1], data[:,-1] #转换数据类型，为了接下来的数学计算

In[7]

y = np.array([1 if i == 1 else -1 for i in y])

In[8]

# 数据线性可分，二分类数据
# 此处为一元一次线性方程
class Model:
    def __init__(self):
        self.w = np.ones(len(data[0])-1, dtype=np.float32)
        self.b = 0
        self.l_rate = 0.1
        # self.data = data
    def sign(self, x, w, b):
        y = np.dot(x, w) + b#求w，b的值
        #Numpy中dot()函数主要功能有两个：向量点积和矩阵乘法。
        #格式：x.dot(y) 等价于 np.dot(x,y) ———x是m*n 矩阵 ，y是n*m矩阵，则x.dot(y) 得到m*m矩阵
        return y
    # 随机梯度下降法
    def fit(self, X_train, y_train):#将参数拟合 X_train数据集矩阵 y_train特征向量
        is_wrong = False #误分类点的意思就是开始的时候，超平面并没有正确划分，做了错误分类的数据。
        while not is_wrong:
            wrong_count = 0
            for d in range(len(X_train)):
                X = X_train[d]
                y = y_train[d]
                if y * self.sign(X, self.w, self.b) <= 0:  # 如果某个样本出现分类错误，即位于分离超平面的错误侧，则调整参数，使分离超平面开始移动，直至误分类点被正确分类
                    self.w =self.w + self.l_rate*np.dot(y, X) #调整w和b
                    self.b = self.b + self.l_rate*y 
                    wrong_count += 1
                if wrong_count == 0:
                    is_wrong = True
                return 'Perceptron Model!'
    def score(self):
        pass

In[9]

perceptron = Model()
perceptron.fit(X, y)#创建感知机模型

In[10]

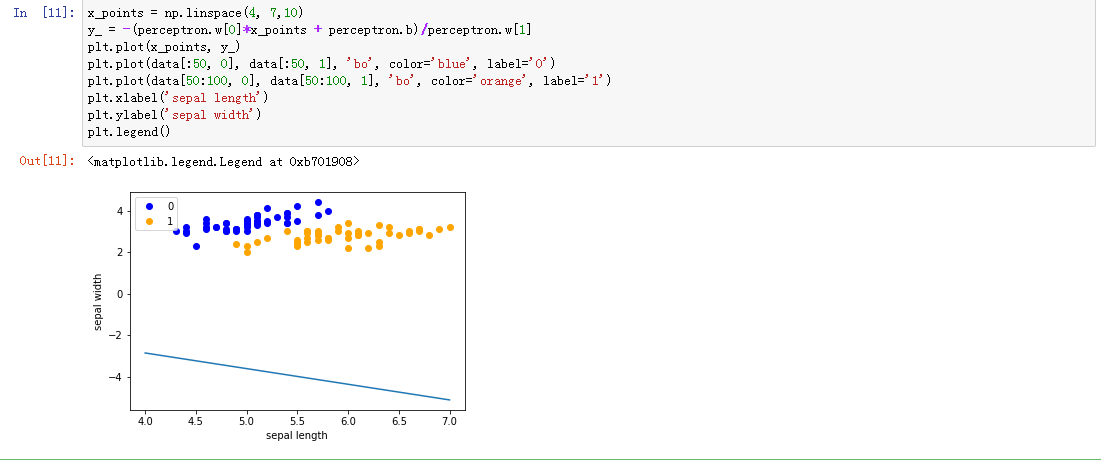
x_points = np.linspace(4, 7,10)
y_ = -(perceptron.w[0]*x_points + perceptron.b)/perceptron.w[1]
plt.plot(x_points, y_)#绘制模型图像
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

In[11]

from sklearn.linear_model import Perceptron#定义感知机

In[12]

clf = Perceptron(fit_intercept=False, max_iter=1000, shuffle=False)
clf.fit(X, y)

In[13]

# Weights assigned to the features.
print(clf.coef_)

In[14]

# 截距 Constants in decision function.
print(clf.intercept_)

In[15]

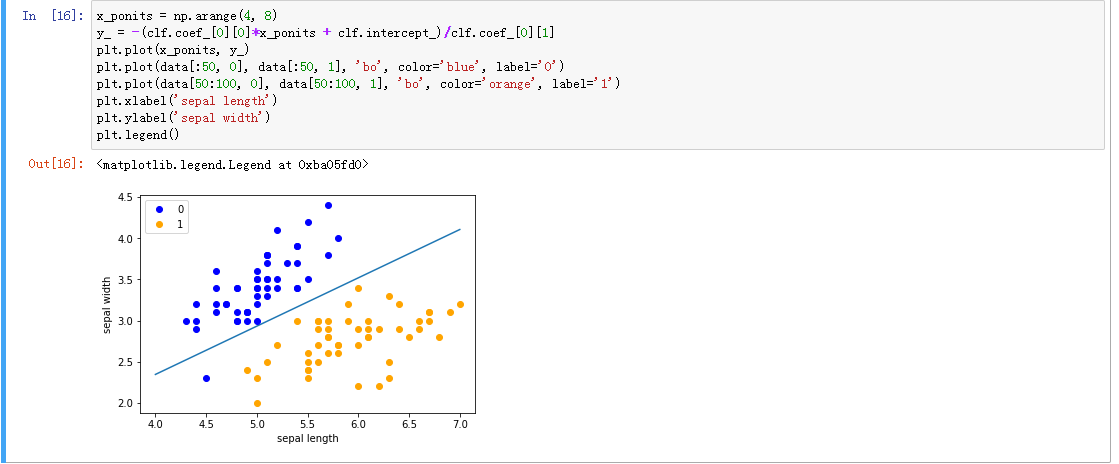
x_ponits = np.arange(4, 8)
y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1]
plt.plot(x_ponits, y_)#确定拟合的图像的具体信息
plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

三、实验小结

通过这次感知器及其应用的实验让我更近一步了解了如何通过python来实现感知器的相关操作。
同时也了解了最小二乘法的相关知识
最小二乘法是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。