HihoCoder第十二周——树上DP

刷油漆

题目

给定一棵树，每个节点有一个权值，将包含1号结点的一部分连通的结点进行涂漆（这里的连通指的是这一些涂漆的结点可以互相到达并且不会经过没有涂漆的结点），使权值和最大。

分析

f(t, m)表示，在以t为根的一棵树中，选出包含根节点t的m个连通的结点，能够获得的最高的评分，然后我们的答案就是f(1, M)。
针对于每一个t，同时求解它的f(t, 0..M)，这样的话，我就可以把m视作背包容量，把每个子结点t_child都视作一件单位重量为1的物品，但是和背包问题不同的是，这件物品的总价值并不是单位价值乘以总重量，而是重量为m_child的该物品的价值为f(t_child, m_child)

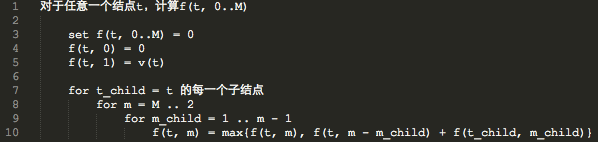
代码

#include <stdio.h>
#include <string.h>
#include <vector>
#include <iostream>
using namespace std;

int n, m, a[101], p[101][101], s, t, used[101];
vector<int> v[101];

void dfs(int k)
{
    for(int i=0; i<v[k].size(); ++i)
    {
        if(used[v[k][i]])
            continue;
        used[v[k][i]] = 1;
        dfs(v[k][i]);
        for(int j=m; j>0; --j)
        {
            for(int x=j; x>0; --x)
                p[k][j] = max(p[k][j],p[k][j-x]+p[v[k][i]][x]);
        }
    }
    for(int i=m; i>0; --i)
        p[k][i] = p[k][i-1] + a[k-1];
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i=0; i<n; ++i)
        scanf("%d", a+i);
    for(int i=0; i<n-1; ++i)
    {
        scanf("%d%d", &s, &t);
        v[s].push_back(t);
        v[t].push_back(s);
    }
    used[1] = 1;
    dfs(1);
    cout<<p[1][m]<<endl;
}