05-无约束优化算法
05-无约束优化算法
凸优化从入门到放弃完整教程地址:https://www.cnblogs.com/nickchen121/p/14900036.html
一、无约束最小化问题
[无约束最小化问题] 使 \(f(x)\) 最小化, \(f:R^n\rightarrow R\) 是凸的,且二次可微(意味着 \(domf\) 是开集)。
假设这个问题是可解的,也就是存在最优点 \(x^*\) ,最优值 \(inf_xf(x)=f(x^*)\) ,记为 \(p^*\) .
[最优充要条件] 因为 \(f\) 是可微且凸的,点 \(x^*\) 是最优点的充要条件是
\(\nabla f(x^*)=0\) .
注:其实可以从二维的图像去理解
因此解决无约束最小化问题等同于寻找上式的解,是含有 \(n\) 个未知数的 \(n\) 个方程的集方程组。有时我们是用递归算法来解决这个问题,也就是依次计算 \(x^{(0)},x^{(1)},...\in domf\) , 有 \(f(x^{(k)})\rightarrow p^*,\)\(k\rightarrow \infty\) 。这样的序列叫做问题的最小化序列 (minimizing sequence)。算法的停止条件: \(f(x^{(k)})-p^*\leq \epsilon\) , \(\epsilon \geq 0\) 是可容许的误差值。
[初始点,下水平集] 初始点 \(x^{(0)}\) 必须在 \(domf\) 中,并且下水平集
\(S=\{x\in domf| f(x)\leq f(x^{(0)})\}\) 必须是闭的。注:下水平集是闭的,其实就是对函数做了水平切割,然后水平切割下的图像是封闭的
如果函数 \(f\) 是闭的(也就是它的所有下水平集都是闭的)那么以上条件都能满足。
- 定义在 \(domf=R^n\) 上的连续函数是闭的,所以如果 \(domf=R^n\) ,那么初始下水平集条件对于任何 \(x^{(0)}\) 都满足 。
- 另一种闭函数:定义域是开集,当 \(x\) 趋近于 \(bd\;domf\) 时, \(f(x)\) 趋近于无限。
[强凸] 一个函数在 \(S\) 上是强凸的,如果存在 \(m>0\) ,使得对于所有的 \(x\in S\) ,有
\(\nabla^2 f(x)\succeq mI.\)
注:强凸的性质,其实就是保证函数的 \(\nabla^2 f(x)\gt 0\) ,也就是确保只有一个最优解,而弱凸是最优解有多个,如下图所示。
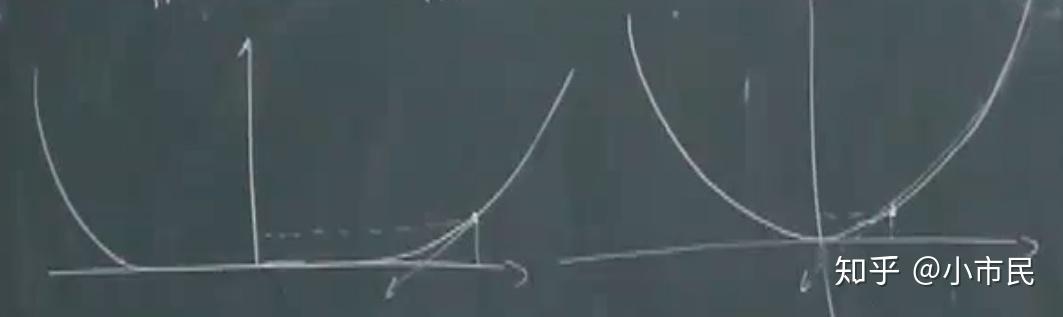
- 对于 \(x,y\in S\) 我们有
\(f(y)=f(x)+\nabla f(x)^T(y-x)+\frac{1}{2}(y-x)^T\nabla^2f(z)(y-x)\) , for some \(z\in [x,y]\) 。
根据强凸的假设,最后一项大于等于 \((m/2)\|y-x\|^2_2, \forall x,y\in S\) ,也就是:
\(f(y)\geq f(x)+\nabla f(x)^T(y-x)+(m/2)\|y-x\|^2_2\) .
当 \(m=0\) 时,我们得到了描述凸性的基本不等式。
当 \(m>0\) 时,我们得到了更好的 \(f(y)\) 的下界。
由于上式中 \(f(x)+\nabla f(x)^T(y-x)+(m/2)\|y-x\|^2_2\) 为 \(y\) 的二次凸函数,因此可以直接令其关于 \(y\) 的导数为 0,即当 \(y=x-(1/m)\nabla f(x)\) 时,上式右侧取最小值,带入可以得到:
- \(p^*\geq f(x)-\frac{1}{2m}\|\nabla f(x)\|^2_2\) . 注:由此可以看到,任何梯度足够小的点都是近似最优解,因为只要有梯度,则可以找到一个更小的 \(p^*\)
- \(\|x-x^*\|_2\leq \frac{2}{m}\|\nabla f(x)\|_2\) .
[次优性条件]:通过 \(p^*\geq f(x)-\frac{1}{2m}\|\nabla f(x)\|^2_2\),我们进行推广,假设存在一个 \(\epsilon \geq \frac{1}{2m} \| \nabla f(x) \|^2_2\),即 \(\| \nabla f(x) \|_2 \leq (2m\epsilon)^{1/2}\),进而推出 \(f(x) - p^* \leq \epsilon\),这就是次优性条件。
[Hessian矩阵的上界] 由于 \(S\) 本身作为一个封闭的下水平集,它不仅有有下界,也会有上界。而且由于 \(\nabla^2f(x)\) 的最大特征值是 \(x\) 在 \(S\) 上的连续函数,因此 \(\nabla^2 f(x)\) 在 \(S\) 上有上界,即存在常数 \(M\) 使得
\(\nabla^2 f(x)\preceq MI,\forall x\in S\) .
- 由此可以得到 \(p^*\leq f(x)-\frac{1}{2M}\|\nabla f(x)\|^2_2\) .
[下水平集的条件数] 对于任意的 \(x\in S\) 有 \(mI\preceq \nabla^2 f(x)\preceq MI\) . 因此 \(\nabla^2f(x)\) 的条件数是比值 \(k=M/m\) 的上界。注:\(M\) 和 \(m\) 是 \(\nabla^2 f(x)\) 的最大特征值和最小特征值
[凸集的宽度] 对于任意范数为1的方向向量 \(q\) ,定义凸集 \(C\subseteq R^n\) 的宽度为:
\(W(C,q)=\underset{z\in C}{sup}\; q^T z-\underset{z\in C}{inf}\; q^Tz.\)
- 最小宽度: \(W_{min}=\underset{\|q\|_2=1}{inf}\, W(C,q).\)
- 最大宽度: \(W_{max}=\underset{\|q\|_2=1}{sup} \, W(C,q).\)
[凸集的条件数] 凸集 \(C\) 的条件数定义为最大宽度和最小宽度的比值:
\(cond(C)= \frac{W^2_{max}}{W^2_{min}}.\)
- \(C\) 的条件数给出了各向异性或离心率的一种测度——条件数小,意味着集合个方向上宽度近似,接近球体;否则集合在某些方向上的宽度远比其他方向上的宽度大。
二、下降法
[下降法 Desent methods] 这种算法给出一个最小化序列 \(x^{(k)}, k=1,...,\)
\(x^{(k+1)}=x^{(k)}+t^{(k)}\Delta x^{(k)}\) ,
\(t^{(k)}>0.\)
- \(\Delta x\) 是一个 \(R^n\) 上的向量,叫做步或搜索方向(search direction),
- \(t^{(k)}>0\) 是步长 (step length), \(k=0,1,...\) 是迭代数。
- 这个方法称为下降法,意味着 \(f(x^{(k+1)})<f(x^{k})\) ,除非 \(x^{(k)}\) 是最优点。
上式可以简写为 \(x^+=x+t\Delta x\) ,或 \(x:= x+t\Delta x\) .
[下降方向] 由凸性可知,如果 \(\nabla f(x^{(k)})^T(y-x^{(k)})\geq 0\) ,那么 \(f(y)\geq f(x^{(k)})\) ,所以搜索方向必须使 \(\nabla f(x^{(k)})^T\Delta x^{(k)}<0\) ,也就是说搜索方向必须和负梯度成锐角,我们称这样的方向为下降方向。
注:\(y\) 是我们搜索的下一个值,相当于 \(x^{(k+1)}\),前面说过如果 \(\nabla f(x^{(k)})^T(y-x^{(k)})\geq 0\),则它们之间形成了一个钝角,那么 \(y\) 在 \(x\) 的等高线和 \(\nabla f(x)\) 之内,即 \(f(y) \geq f(x^{(k)})\)
[算法]:给定一个初始点 \(x\in domf\) . 重复:
- 决定下降方向 \(\Delta x\) .
- 直线搜索: 选择步长 \(t\) , \(t>0\)
- 迭代 \(x:=x+t\Delta x\) .
直到满足停止条件。
- 停止条件一般是 \(\|\nabla f(x)\|_2\leq \eta\) , \(\eta\) 是一个小的正数。
注:这里可以参考次优性条件,通过 \(p^*\geq f(x)-\frac{1}{2m}\|\nabla f(x)\|^2_2\),我们进行推广,假设存在一个 \(\epsilon \geq \frac{1}{2m} \| \nabla f(x) \|^2_2\),即 \(\| \nabla f(x) \|_2 \leq (2m\epsilon)^{1/2}\),进而推出 \(f(x) - p^* \leq \epsilon\)
[直线搜索 line search] 有几种方法:
- 精确直线搜索(Exact line search):
沿着射线 \(\{x+t\Delta x| t\geq 0\}\) 寻找使 \(f\) 取最小值的 \(t\) :
\(t=\underset{s\geq 0}{argmin}\, f(x+s\Delta x)\) .
注:其实这里就是寻找一个下降最多的方向,确保每次都有下降
- 回溯直线搜索(Backtracking line search):
在每一步,从单位步长开始,不断尝试减小步长 (用小于1大于零的系数乘 \(t\) ),直到
\(f(x+t\Delta x)\leq f(x)+\alpha t \nabla f(x)^T \Delta x\)
注:回溯直线从单位步长开始按比例减小,并且只要求最后满足停止条件即可,而且当 \(t\) 足够小的时候,一定是可以满足停止条件的。
如图,回溯搜索最终要使 f 落在两个虚线之间。注:注意该图的横轴是 \(t\),不是 \(x\)
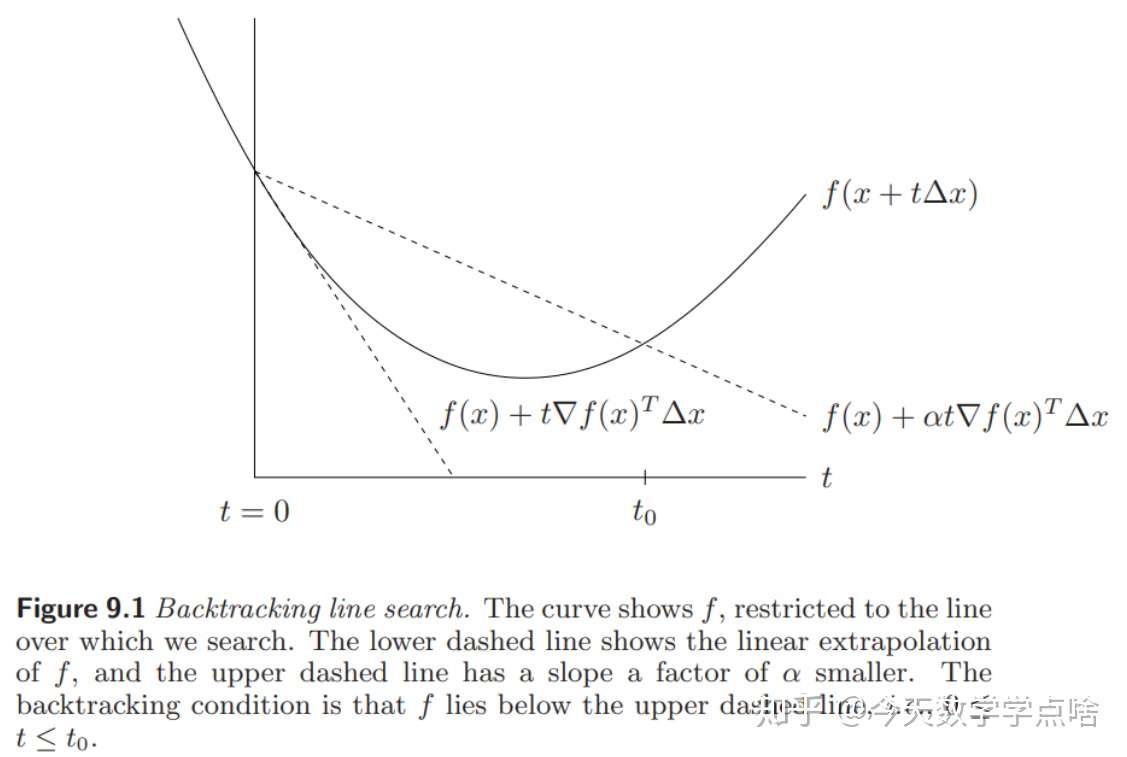
三、梯度下降法
注:梯度下降法就是在下降法的角度上明确了下降的方向为 \(- \nabla f(x)\)
[梯度下降法] 关于搜索方向,一种自然的选择是 \(\Delta x=-\nabla f(x)\) . 这种算法叫做梯度下降法。
[算法] 给定一个初始点 \(x\in domf\) . 重复:
- \(\Delta x:= -\nabla f(x)\) .
- 直线搜索:用exact/backtracking 搜索方法选择步长 \(t\) .
- 迭代, \(x:=x+t\Delta x\) .
直到满足停止条件。
- 停止条件一般是 \(\|\nabla f(x)\|_2\leq \eta\) , \(\eta\) 是一个小的正数。在第一步之后检查停止条件而不是迭代之后。
[收敛性分析]
直观讲,梯度法收敛速度很大取决于函数等值线的形状,如果比较圆(各向宽度均匀)那么从任一点开始都更快到达中心注:圆的话,直接往圆心走就行了,这就是未来牛顿法想要做到的,比较扁的话,就需要很多步才能到达。等值线的形状用集合最大宽度和最小宽度的比值来衡量,因此这个比值很关键,以下是推导:
- 对于函数 \(f\) ,存在常数 \(L \geq 0\) 使得 \(h^T\nabla^2 f(x)h\leq L\|h\|^2 , \forall y\) ,
\(\begin{equation}\begin{split}f(x+\alpha h)-f(x) &=\int^{\alpha}_{0} \nabla f^T(x+\tau h)h\; d\tau \\ &= \alpha \nabla f^T(x)h+\int^{\alpha}_0 (\nabla f^T(x+\tau h)-\nabla f^T(x))h\;d\tau\\&=\alpha\nabla f^T(x)h+ \int^{\alpha}_0 [\int^{\tau}_0 h^T \nabla^2 f(x+sh)h \; ds]\;d\tau\\ &\leq \alpha \nabla f^T(\alpha)h + L\|h\|^2\int^{\alpha}_0 \tau\; d\tau \end{split} \end{equation}\)
令 \(h=-\nabla f\) 得,
\(\begin{equation}f(x+\alpha h)-f(x) \leq -\alpha\|\nabla f(x)\|^2 + \frac{\alpha^2L}{2}\|\nabla f(x)\|^2 = (\frac{\alpha^2L}{2} -\alpha)\|\nabla f(x)\|^2 \end{equation}\)
为了使右边最小,令其关于 $\alpha $ 的导数为0 ,得到 \(\alpha^* =\frac{1}{L}\) ,代回不等式,
\(\begin{equation}\begin{split}f(x+\alpha h)-f(x) &\leq -\frac{1}{2L}\|\nabla f\|^2\end{split} \end{equation}\) .
注:此处用的不是书上的推导,但是从上可以看出,最后 \(\begin{equation}\begin{split}f(x+\alpha h)-f(x) &\leq -\frac{1}{2L}\|\nabla f\|^2\end{split} \end{equation} \leq 0\),也就是说 $ f(x+ \alpha h) \leq f(x)$
- 非凸函数收敛性:
\(\sum ^M_{k=0} (f(x^{k+1})-f(x^{k}))\leq -\frac{1}{2L}\sum^M_0\|\nabla f(x^{k})\|^2\)
不等式左边等于 \(f(x^{M}-f(x^0))\) ,根据上一步得到的不等式有
\(\frac{1}{2L} \sum^M_{k=0} \|\nabla f(x^k)\|^2\leq f(x^0)-f(x^M)\leq C\)
因此当 \(k\rightarrow \infty,\) 梯度 \(\|\nabla f(x^k)\|\rightarrow 0\) ,收敛速度线性 \(\|\nabla f(x^k)\|^2\sim O(\frac{1}{k})\) 。
- 凸函数收敛性:
令 \(f\) 是凸函数: \(\forall x,y\in R^n 有 f(y)-f(x)\geq \nabla f^T(x)(y-x).\) 最优点 \(x^*\)
\(\begin{equation}\begin{split} \|x^{k+1}-x^*\|^2 &= \|x^k -\alpha \nabla f(x^k)-x^* \|^2\\ &= \|x^k -x^*\|^2 -2\alpha \nabla f^T(x^k)(x^k-x^*)+\alpha^2\|\nabla f(x^k)\|^2\\ &\leq \|x^k-x^*\|^2+2\alpha(f(x^*)-f(x^k))+\alpha^2\|\nabla f(x^k)\|^2 \end{split}\end{equation}\)
两边求和从 \(k=0\) 加到 \(k=M\) ,
$ |xM-x|^2\leq |x0-x|^2+2\alpha \sumM_{k=0}(f(x*)-f(xk))+\alpha2\sum^M_{k=0}|\nabla f(xk)|2.$
因为是凸函数 \(f(x^*)-f(x^k)\geq \nabla f^T(x^k)(x^*-x^k)\) ,所以有
\(\sum^M_{k=0}f(x^k)-f(x^*)\leq \infty\) ,函数收敛, \(f(x^k)-f(x^*)\sim O(\frac{1}{k})\) 收敛速度为线性。
- 强凸函数收敛性:
令 \(f\) 是强凸函数: \(\exists \lambda>0, \forall x : h^T\nabla^2 f(x)h\geq \lambda \|h\|^2.\)
由强凸函数的定义有
\(f(y)-f(x)\geq \nabla f(x)^T(y-x)+\frac{\lambda}{2}\|y-x\|^2.\)
记函数最小值为f^*,
\(f^*-f(x)\geq \underset{y\in R^n}{min} (\nabla f(x)^T(y-x)+\frac{1}{2}\lambda\|y-x\|^2).\)
对右边求导 \(\nabla f(x)+\lambda(y-x)=0\) , 得 \(y-x=-\frac{\nabla f(x)}{\lambda}\)
带回得,
\(f^*-f(x)\geq -\frac{\|\nabla f(x)\|^2}{\lambda} + \frac{\lambda\|\nabla f(x)\|^2}{2\lambda^2} = -\frac{\|\nabla f(x)\|^2}{2\lambda}\)
\(2\lambda(f^*-f(x))\geq -\|\nabla f(x)\|^2\)
因此有,
\(f(x+\alpha h)-f(x)\leq -\frac{1}{2L}\|\nabla f(x)\|^2\leq \frac{\lambda}{L}(f^*-f(x))\)
$\begin{equation}\begin{split} f(x+\alpha h)-f^* &\leq f(x)-f*-\frac{\lambda}{L}(f(x)-f) \ & = (1-\frac{\lambda}{L})(f(x)-f^)\ & \leq (1-\frac{\lambda}{L})(f(x0)-f*)\end{split}\end{equation} $
由此,线性收敛,收敛快慢(步数)取决于 \(\frac{\lambda}{L}\) :
如果 \(\frac{\lambda}{L}\sim 1\) ,那么 \(1-\frac{\lambda}{L} << 1\) ,迭代次数少。
如果 \(\frac{\lambda}{L} << 1\) ,那么 \(1-\frac{\lambda}{L} \sim 1\) ,迭代次数多。
- 几何解释:
注:上述推导公式有兴趣的可以琢磨,我这里就说说最后推导除了什么。回顾第1节提到的:凸集最大宽度 \(M\) 和最小宽度 \(m\) ,可以把强凸系数 \(\lambda\) 看作是最小宽度 \(m\) ,而利普希兹常数 \(L\) 看作是最大宽度 \(M\) . 他们的比值反映了凸集的形状。也就是说条件数对梯度下降的收敛性影响非常大,因为条件数控制了函数等高线的形状
如果 \(\lambda\) 和 \(L\) 数值相近,也就是最大最小宽度差不多 ,函数等值线接近圆(球),那么任一点的下降方向都比较接近中心,因此不论使用精确直线搜索还是回溯直线搜索都能沿着比较直的路更快下降到中心。
注:怎么去看下面三张图呢,牢记,三张图画的都是函数的等高线。也就是说,梯度下降只是沿着当前点 \(x_0\) 的负梯度方向 \(-\nabla f(x)\) 找比自己当前点更小的点 \(x_1\),如果函数等高线更接近圆,负梯度方向指向圆心(圆边上的任意点的支撑超平面也就是 \(-\nabla f(x)\) 都指向圆心),那么无论步长 \(\alpha\) 怎么设定,都是往最小值(圆心)方向走过去;如果函数等高线接近椭圆,负梯度方向就不一定指向最小值,如果步长再设置大点,那么往往会偏离最小值,这也是为什么初始点设置的重要性,而接下来的最速下降方法和牛顿法就是为了解决这个问题。
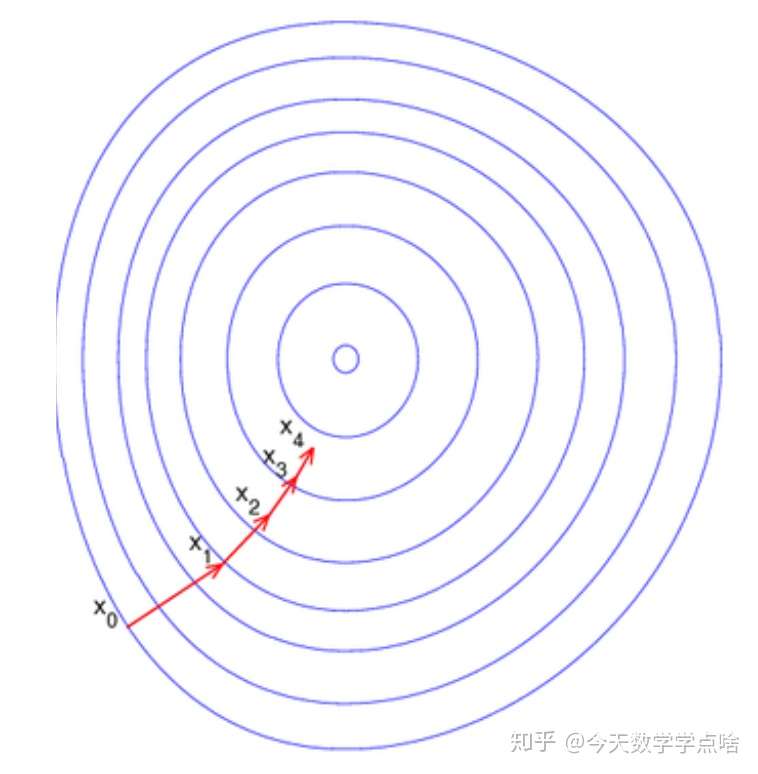
反之如果大小宽度相差较多,那么函数等值线更不均匀,比如一个很扁的椭球,此时某些点上的下降方向非常偏离中心(起始点的选取变得重要),因此下降的道路会比较曲折,例如下面第一张图。但有时用精确直线搜索会改善这种情况,见第二张图。
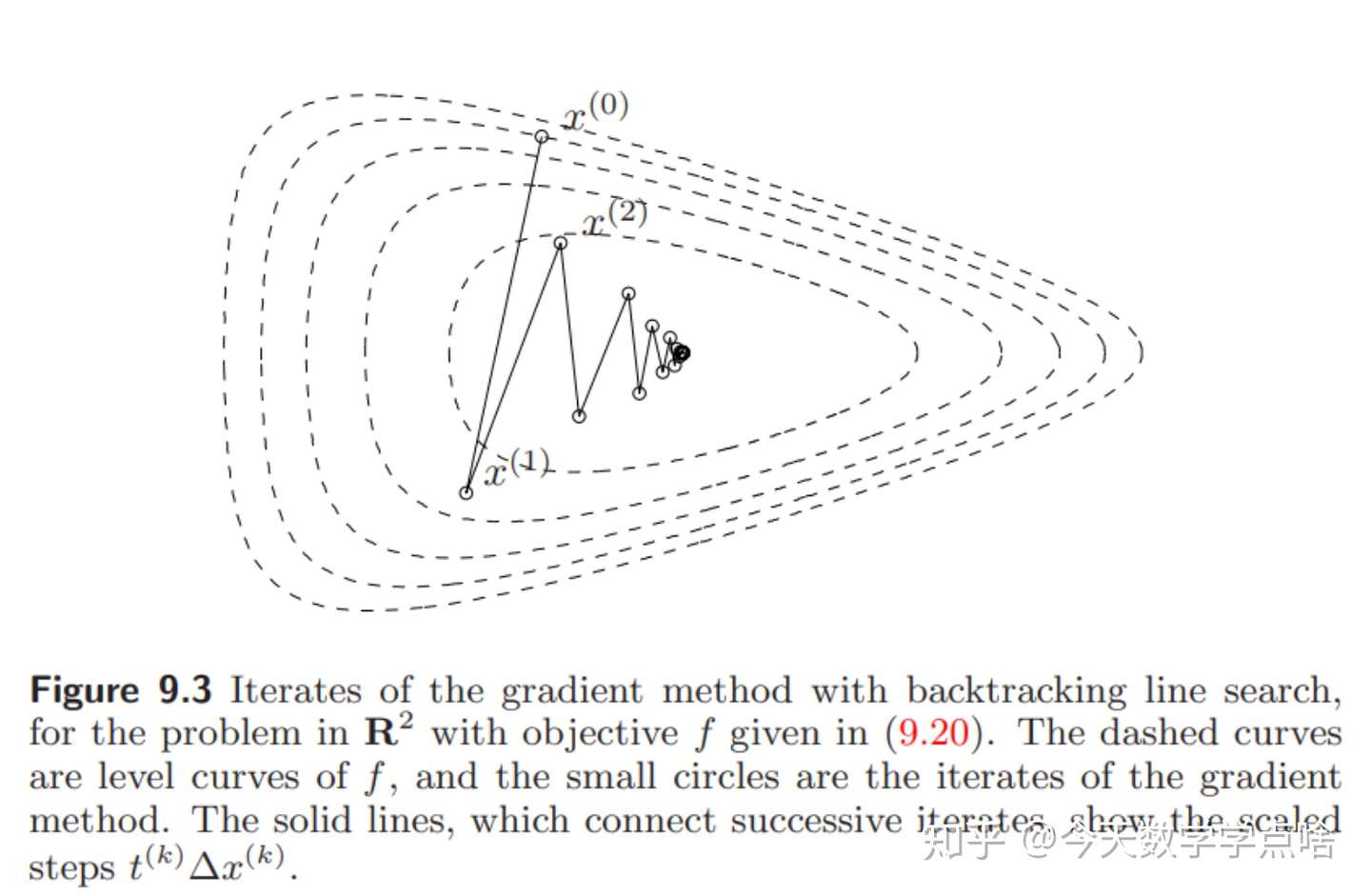
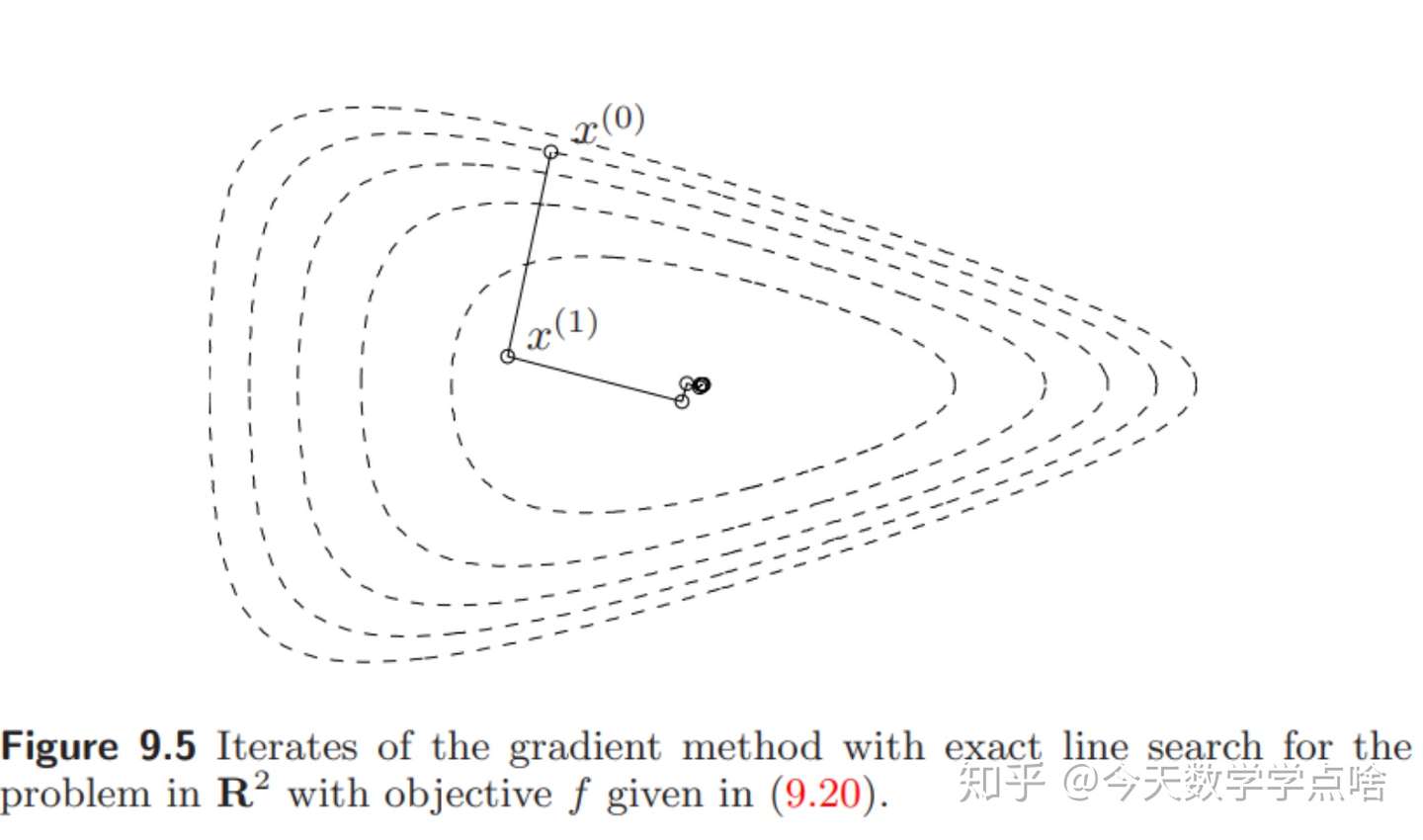
[结论]
- 梯度下降法一般是线性收敛的(linear convergence) ,误差 \(f(x^{(l)})-p^*\) 收敛到 \(0\) 近似于一个几何级数。
- 如果用回溯直线搜索的话, \(\alpha,\beta\) 对收敛效果有影响但没有非常大,精确直线搜索有时能够改善收敛,但是效果不是很大。
- 收敛速度极大地取决于Hessian矩阵或下水平集的条件数。
- 梯度下降法的主要优势在于简单,劣势是收敛速度依赖于Hessian矩阵或下水平集的条件数。
四、最速下降法
注:书中大多数计算涉及范数运算,想看懂书上的推导过程可以学习书中附录范数的运算。主要就是把握最速下降法的核心思想:在每次下降的过程中,不再单纯的沿着 \(-\nabla f(x)\) 的方向下降,而是沿着被 \(p\) 范数约束下的 \(- \nabla f(x)\) 的方向下降,进而让下降速度变得更快。而对偶范数能控制下降方向的原因,很大程度取决于对偶范数的定义——\(\|z\|_*=\sup\{z^T x| \|x\|\leq 1\}\),可以发现,和最速下降方向的定义非常相似
[方向导数 directional derivative] \(f(x+v)\) 在 \(x\) 附近的一阶泰勒展开式: \(f(x+v)\approx \hat{f}(x+v)=f(x)+\nabla f(x)^Tv.\)
注:依据泰勒展开式,\(v = x+v - v\)。
第二项 \(\nabla f(x)^Tv\) 叫做 \(f\) 在 \(x\) 处以 \(v\) 为方向的方向导数。
注:它给出了走一小步 \(v\) 之后 \(f\) 的近似,这一步 \(v\) 是下降的方向,如果方向导数是负的。问题是如何选择 \(v\) 使得方向导数尽可能地负(小)。我们可以让 $v $ 充分大,但为了让问题有意义,我们还是必须得限制 \(v\) 的大小,这也就是后面范数的由来。
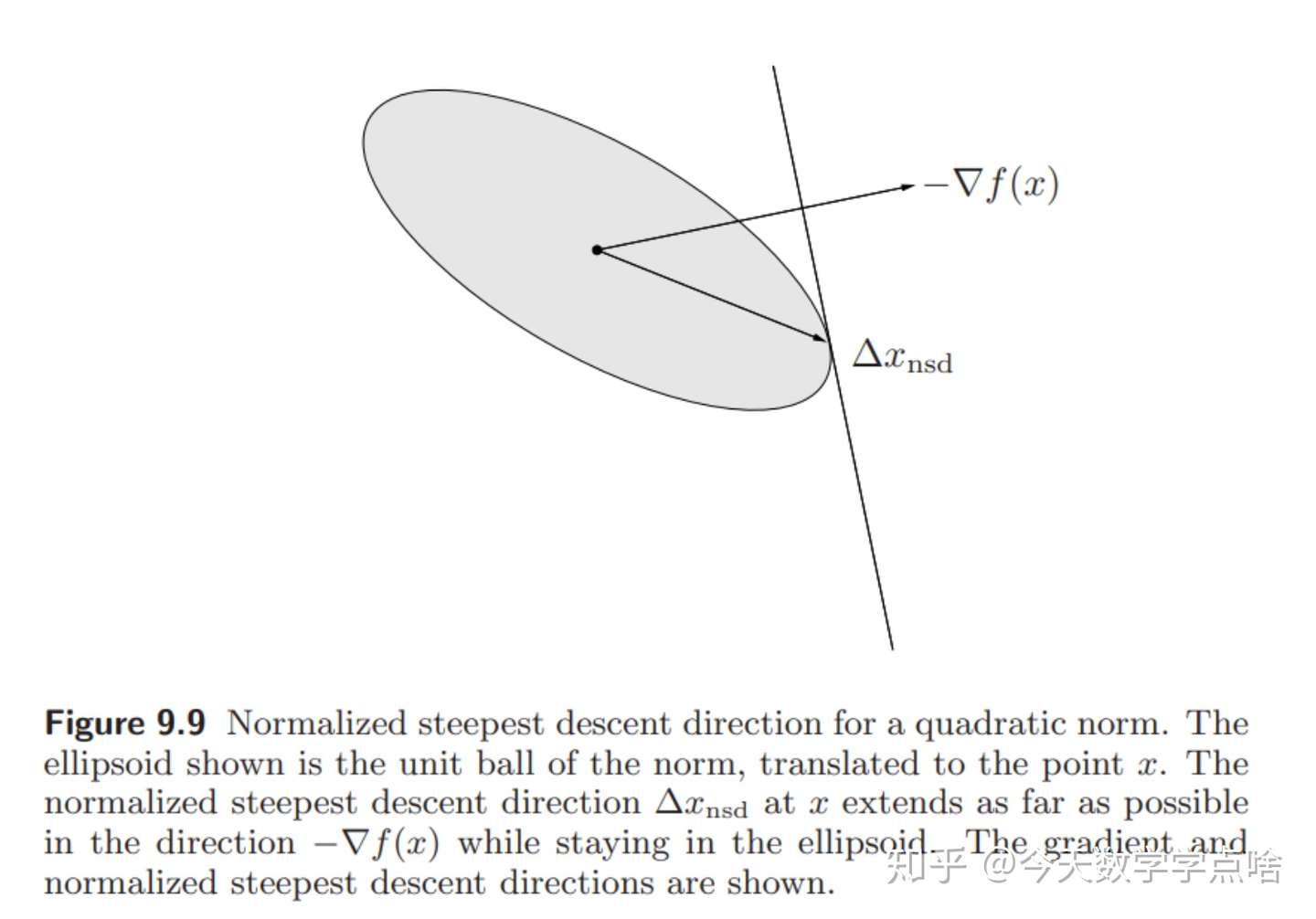
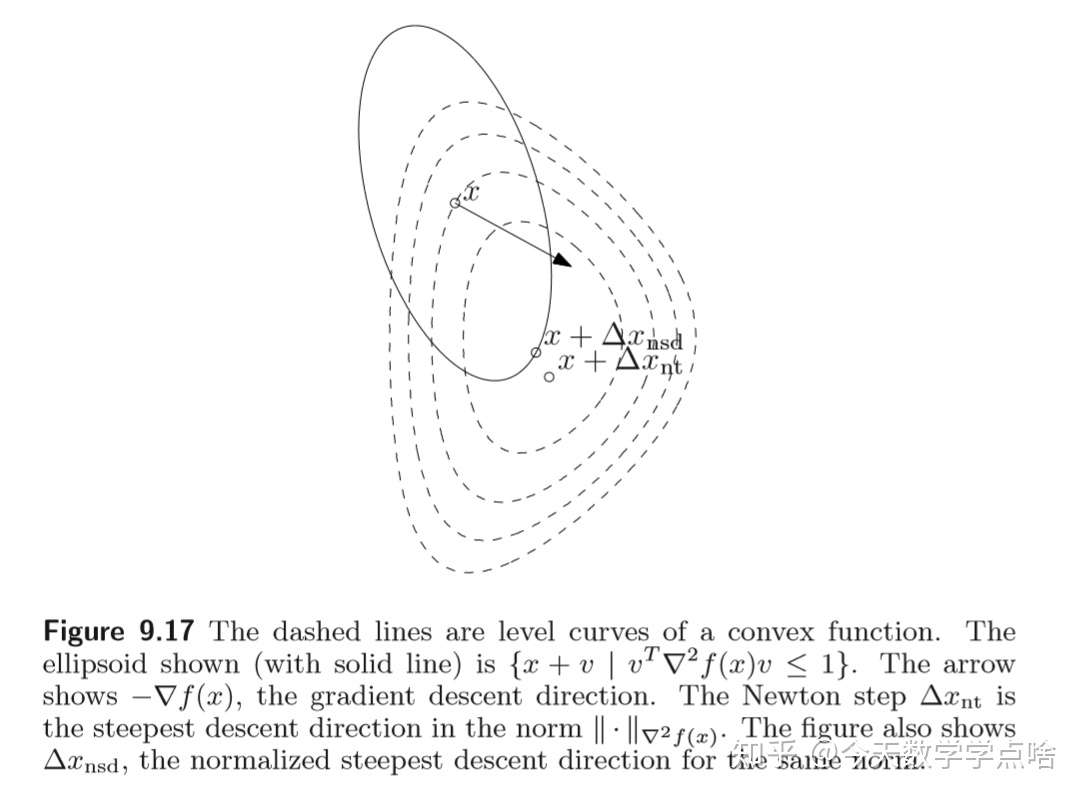
[规范化最速下降方向 normalized steepest descent direction]
令 \(\|\cdot\|\) 是 \(R^n\) 上的任意范数,我们定义一个规范化的最速下降方向为: \(\Delta x_{nsd}=argmin\{\nabla f(x)^Tv \;| \; \|v\|=1\}\) .注:使用 \(argmin\) 的原因是因为 \({\nabla f(x)}^T v\) 越小,则下降的越多,并且也有可能有多个最小值(取一个),也符合我们最速下降的思想
规范化最速下降方向 \(\Delta x_{nsd}\) 是单位长度的一步,使得 \(f\) 的线性近似下降最多。
几何解释:注:这是理解未来图像的重要知识点,最速下降方向是,在单位球 \(\|\cdot\|\) 内的所有方向中,在向量 \(-\nabla f(x)\) 上投影最长的那个方向。
[最速下降方向] 缩放规范化最速下降方向,得到一个未规范化的最速下降方向:
\(\Delta x_{sd}=\|\nabla f(x)\|_* \Delta x_{nsd}\) ,
\(\|\cdot\|_*\) 是对偶范数(dual norm),注:其中对偶范数 \(\| \nabla f(x) \|_* \nabla x_{nsd}\) 是一个特殊的比例因子,让其非规范化。
[最速下降的量]
\(\nabla f(x)^T \Delta x_{sd}=\|\nabla f(x)\|_* \nabla f(x)^T \Delta x_{nsd}=-\|\nabla f(x)\|^2_*\) .
[最速下降法] 最速下降法使用最速下降方向为搜索方向。
[算法] 给定一个初始点 \(x\in domf\) ,重复:
- 计算最速下降方向 \(\Delta x_{sd}\) .
- 直线搜索:通过backtracking/exact 直线搜索方法选择 \(t\) .
- 迭代 \(x:=x+t\Delta x_{sd}\) .
直到满足停止条件。
- 当使用精确直线搜索时,下降方向的缩放没有效果,所以可以用规范化的下降方向或者非规范化的下降方向。
[关于欧几里得范数(l2 范数)的最速下降] 如果使用欧几里得范数, \(\Delta x_{sd}=-\nabla f(x)\) ,所以此时最速下降法就是梯度下降法。
注:一个单位向量与梯度内积的最小值是当单位向量的方向为负梯度方向。通过这个公式可以理解,\(\nabla^T f(x) v = \|\nabla^T f(x)\|_2 ||v||_2 cos\theta\),其中由于为欧几里得范数 \(\|v\|_2 = 1\),取最小值时就是 \(\cos\theta = -1\),进而可以推出 \(\nabla x _{sd} = v = - \nabla f(x)\)
[关于二次-P范数的最速下降] 考虑二次范数 \(\|z\|_P=(z^TPz)^{1/2}=\|P^{1/2}_z\|_2\) , \(P\in S^n_{++}.\) 那么规范化的最速下降方向是:
\(\Delta x_{nsd}=-(\nabla f(x)^TP^{-1}\nabla f(x))^{-1/2} P^{-1}\nabla f(x)\) .
对偶范数 \(\|z\|_*=\|P^{-1/2}z\|_2\) ,所以最速下降方向为:
\(\Delta x_{sd}=-P^{-1}\nabla f(x).\)
注:二次-P 范数下的最速下降方向可以理解为对原问题进行坐标变换 \(\hat x = P^{1/2} x\) 后的梯度方向。
注:下图中椭圆中的所有向量中, \(\Delta x_{nsd}\) 是在 \(-\nabla f(x)\) 方向上投影最长的向量。
[关于 \(l_1\) -范数的最速下降] 关于 \(l_1\) -范数的,规范化最速下降方向为:
\(\Delta x_{nsd}=argmin\{\nabla f(x)^T v \;| \|v\|_1\leq 1\}\) .
令 \(i\) 为任意index, \(\|\nabla f(x)\|_{\infty} = |(\nabla f(x))_i|\) ,那么规范化的最速下降方向:
\(\Delta x_{nsd}=-sign(\frac {\partial f(x)}{\partial x_i})e_i\) .
\(e_i\) 是第 \(i\) 个标准基向量,那么一个非规范化的最速下降方向为:
\(\Delta x_{sd} = \Delta x_{nsd}\|\nabla f(x)\|_{\infty}=-\frac{\partial f(x)}{\partial x_i} e_i\) .
注:于是关于 \(l_1\) 范数的最速下降步总是一个标准基向量,是使 \(f\) 下降最多的坐标轴的方向。如下图:
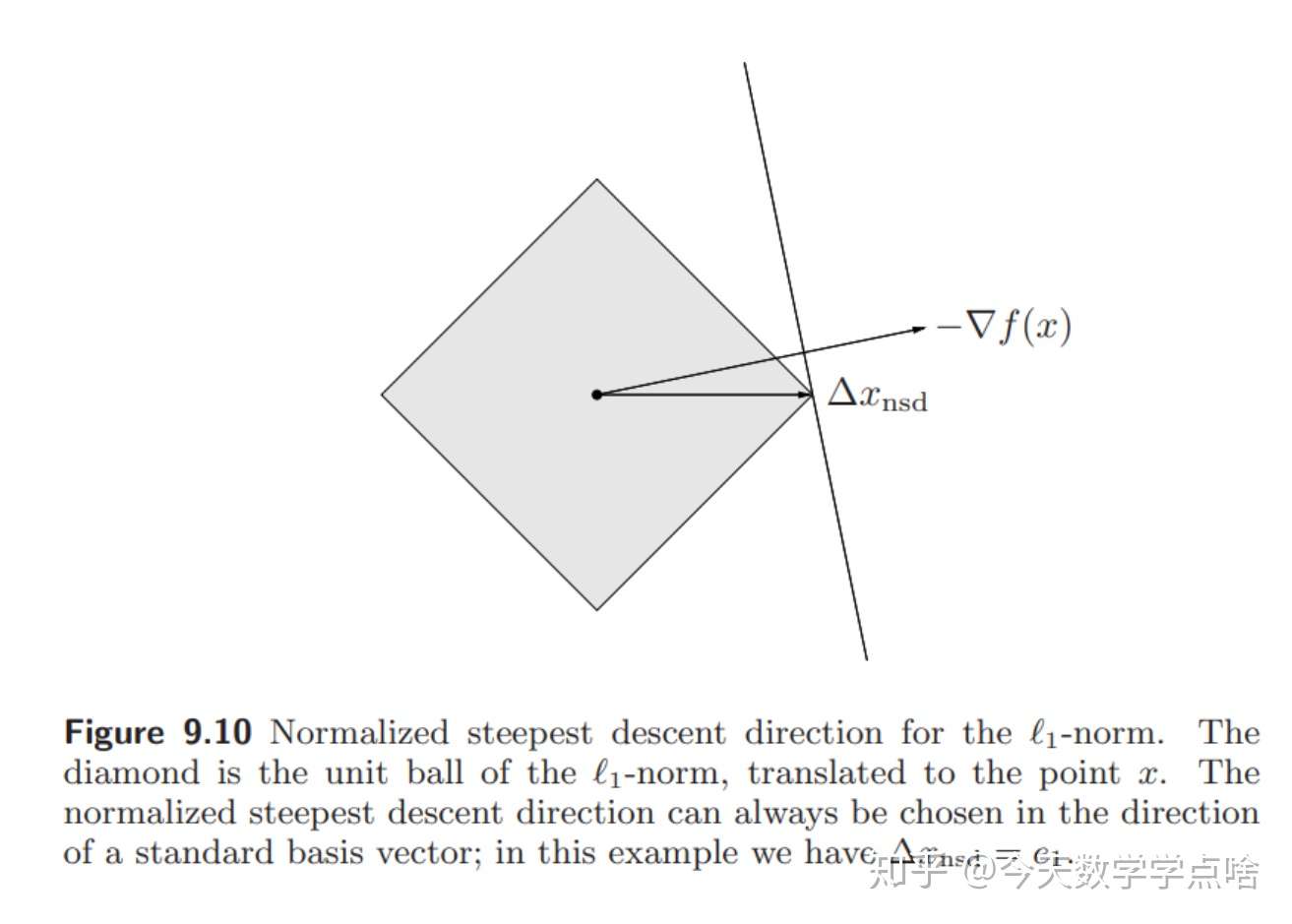
\(l_1\) 最速下降的解释:梯度在所有坐标轴上投影的最大值所对应的坐标轴的反方向。每个迭代中,选择 \(\nabla f(x)\) 中具有最大绝对值的元素(分量),然后根据 \((\nabla f(x))_i\) 的符号,增加或减少 \(x\) 中对应的元素。这种算法有时也称为坐标下降,因为每次只更新 \(x\) 的一个元素(分量)。
[收敛性] 有着和梯度方法一样的线性收敛性。
五、牛顿法
[牛顿步程 newton step] 对于 \(x\in domf\) , 向量
\(x_{nt}=-\nabla^2 f(x)^{-1}\nabla f(x)\)
叫做牛顿步程 ( \(f\) 在点 \(x\) 处的)。
因为 \(\nabla ^2 f(x)\) 是非负的,所以
\(\nabla f(x)^T\Delta x_{nt}= -\nabla f(x)^T \nabla^2f(x)^{-1}\nabla f(x)<0.\)除非 \(\nabla f(x)=0\) ,
所以牛顿步程是下降的方向(除非 \(x\) 是最优点)。
注:牛顿步程可以区别于最速梯度下降法的下降方向
[解释]
- 牛顿步程使得 \(f\) 在 \(x\) 附近的二次泰勒近似最小化。\(\hat{f}(x+v)=f(x)+\nabla f(x)^T v+\frac{1}{2}v^T \nabla ^2 f(x)v\) .
注:对上述关于 \(v\) 的二次凸函数求导,可以发现在 \(v=\Delta x_{nt}\) 时取最小值。
如图,虚线表示函数的二次近似,它在越接近最低点的地方误差越小。
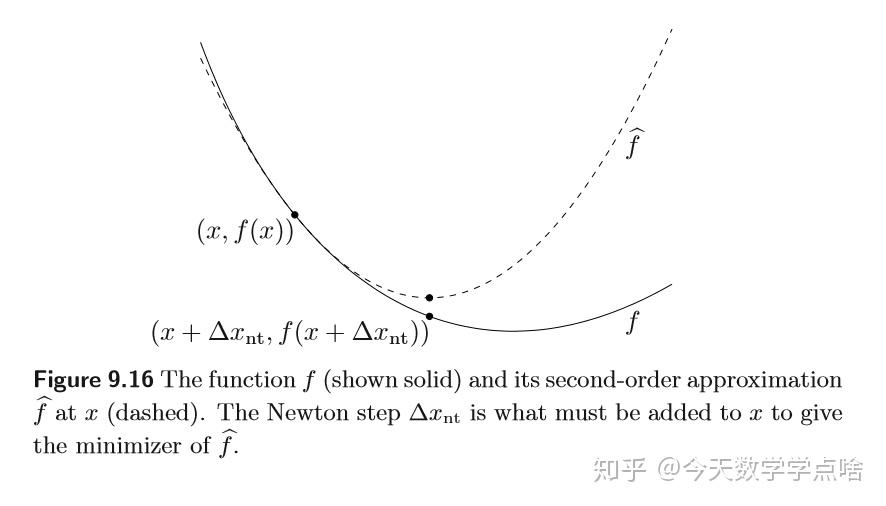
注:牛顿法其实就是函数 \(f\) 的二阶近似后求近似解
- 牛顿步程也是由Hessian矩阵 \(\nabla ^2 f(x)\) 定义的二次范数,也就是
\(\|u\|_{\nabla^2 f(x)}=(u^T \nabla^2 f(x)u)^{1/2}\) 的最速下降方向。
当 \(x\) 接近 \(x^*\) 时,牛顿步程是搜索方向的好选择。注:这里还是涉及范数运算,我直接套用书中的话,由于由于采用 \(\| \cdot \|_{\nabla^2 f(x)}\),这样进行坐标变换后的 Hessian 矩阵的条件数小,收敛速度很快,并且当 \(x\) 靠近 \(x^*\) 时,有 \(\nabla^2f(x) \approx \nabla^2 f(x^*)\)
如图,图中箭头表示负梯度 \(-\nabla f(x)\) ,实线椭圆是 ${x+v| vT\nabla2 f(x)v\leq 1} $ ,代表了点 \(x\) 处在 \(\nabla^2f(x)\) 定义的范数下的所有可选方向,而其中在 $-\nabla f(x) $ 上投影最长的方向是最速下降方向。
- 牛顿步程是线性最优条件的解。如果我们把最优条件(KKT 条件) \(\nabla f(x)=0\) 线性化 得到,
\(\nabla f(x+v)\approx \nabla f(x)+\nabla^2 f(x)v=0.\)
通过上式可以求出 \(v = {\nabla^2 f(x)}^{-1}f(x)\)
这是关于 \(v\) 的线性方程,它的解是 \(v=\Delta x_{nt}.\) 如图(注:横轴是 0 轴,函数 \(f\) 的二阶泰勒展开的函数 \(\hat f\) 导数为 0 的值和函数 \(f\) 的值近似):

[牛顿减量] 在点 \(x\) 处的牛顿减量定义为
\(f(x)- \inf_y \hat f (y) = f(x) - \hat f(x+\nabla x_{nt})=\frac{1}{2}\lambda(x)^2\) .
\(\lambda(x)= (\nabla f(x)^T\nabla^2f(x)^{-1}\nabla f(x))^{1/2} .\)
\(\nabla f(x)^T \nabla x_{nt} = -\lambda(x)^2\)
[牛顿法] 纯牛顿法步长固定为 \(t=1\) ,以下介绍阻尼牛顿法( damped Newton method or guarded Newton method)。
[阻尼牛顿法算法] 给定起始点 \(x\in domf\) ,容许误差 \(\epsilon >0\) ,
- 计算牛顿步程 \(\Delta x_{nt}\) 和牛顿减量 \(\lambda^2\) 。
- 停止条件:如果 \(\lambda^2/2<\epsilon\) 则退出。
- 直线搜索:用回溯直线搜索选择步长 \(t\) 。
- 迭代: \(x:=x+t\Delta x_{nt}\) .
六、牛顿法收敛性分析
设函数 \(f\) 满足条件:
- 二次可微.
- 强凸, \(h^T\nabla^2f(x)\geq m \|h\|^2\) , \(\forall x\in S\) .
- 存在 \(M>0\) , \(\forall x\in S\) .
- \(f\) 的Hessian矩阵在 \(S\) 上满足 Lipschitz 连续:存在常数 \(L\) 使得 \(\|\nabla^2 f(x)-\nabla^2f(y)\|\leq L\|x-y\|.\) (也可看作 \(f\) 的三阶导数的界,其中 \(L\) 是对 \(f\) 与其二次模型之间近似程度的一种度量)
阻尼阶段
此阶段所有步长 \(\alpha<1\) ,称为阻尼阶段。
\(\begin{equation}\begin{split}f(x+\alpha \Delta x_{nt}) &\leq f(x)+\alpha \nabla f(x)^T \Delta x_{nt} + \frac{\alpha^2M}{2}\| \Delta x_{nt}\| \\ &\leq f(x)=\alpha \lambda ^2 + \frac{\alpha^2 M}{2} \frac{1}{m} \Delta x_{nt}^T \nabla^2f(x)\Delta x_{nt}\\&=f(x)=\alpha\lambda^2 + \frac{\alpha^2M}{2m}\lambda^2\\&= f(x)-\lambda^2(\alpha -\frac{\alpha^2M}{2m})\end{split}\end{equation}\)
令 \((\alpha -\frac{\alpha^2M}{2m})\) 关于 \(\alpha\) 的导数为零,得 \(\alpha^*=\frac{m}{M}\) ,代回,
\(f(x+\alpha \Delta x_{nt})\leq f(x)-\frac{m}{2M}\lambda^2.\)
二次收敛阶段
此阶段每步步长都为 \(\alpha=1\) , 是纯牛顿法阶段, 收敛很快,所以叫二次收敛阶段。
令 \(\xi\in (x,x+\alpha \Delta x_{nt})\) ,
\(\begin{equation}\begin{split} f(x+\alpha \Delta x_{nt})&\leq f(x)-\alpha\lambda^2 +\frac{\alpha^2}{2}\Delta x_{nt}^T \nabla^2 f(\xi) \Delta x_{nt}\\&= f(x)-\alpha \lambda^2 +\frac{\alpha^2}{2}\lambda^2 + \frac{\alpha^2}{2}\Delta x_{nt}^T(f(\xi)-\nabla^2f(x))\Delta x_{nt} \\&\leq f(x)-\alpha\lambda^2 + \frac{\alpha^2}{2} + \frac{\alpha^3}{2}L\|\Delta x_{nt}\|^3 \end{split}\end{equation}\)
由于强凸性和 \(\lambda^2\) 的定义有: \(\lambda^2\geq m\|\Delta x\|^2\) . 所以 \(\|\Delta x\|^3\leq \frac{\lambda^3}{m^{3/2}}\) .
再令 \(\alpha=1\) 得,
\(f(x+ \Delta x_{nt}) \leq f(x)-\lambda^2(\frac{1}{2}-\frac{L\lambda}{2m^{3/2}})\leq f(x)-\frac{\lambda^2}{4}\) .
注:上述没有详细解释为什么收敛会极其迅速,这里通过书中的一段公式来做一个介绍,设有迭代次数 \(l\) 和 \(k\),且 \(l \geq k\),则会有一个公式 P466 公式 9.35 \(f(x^{(l)}) - p^* \leq \frac{1}{2m} \|\nabla f(x^{(l)}) \|^2_2 \leq \frac{{2m}^3}{L^2}(\frac{1}{2})^{2^{l-k+1}}\),从上式中可以看出,在足够多的迭代以后,每次迭代都能使正确数字的位数翻番,也就是说收敛速度是极其迅速的。
\(f(x^{(l)}) - p^* \leq \frac{1}{2m} \|\nabla f(x^{(l)}) \|^2_2 \leq \frac{{2m}^3}{L^2}(\frac{1}{2})^{2^{l-k+1}}\) 同时表明一旦算法进入纯 Newton 阶段, \(l \to \infty\) 时, \(f(x_l) - f(p^*) \to 0\) 。此外给定精度 \(\epsilon\) ,我们可以得到收敛次数 \(n\) 为
\(n = \log_2 \log_2 (\epsilon_0 / \epsilon), \quad \epsilon_0 =2m^3/L^2 \\\)
其表明在纯 Newton 阶段,算法将收敛非常快(远大于Gradient Descent的收敛速度),对于任意凸函数,我们可以假定纯 Newton 阶段需要的收敛次数为5或6。
在这篇文章里,我们介绍了 Newton Method,证明了 Newton Method 是一个收敛非常快的方法。那是不是 Newton Method 的收敛时间就要小于 Gradient Descent 呢?No!因此 Newton Method 每一步要计算 \({\nabla^2 f(x)}^{-1}\),这显然是一个非常耗时的操作!
参考文献:Stephen Boyd, Lieven Vandenberghe: Convex Optimization


 浙公网安备 33010602011771号
浙公网安备 33010602011771号