03-凸优化问题
03-凸优化问题
凸优化从入门到放弃完整教程地址:https://www.cnblogs.com/nickchen121/p/14900036.html
一、一般优化问题
一般优化问题的形式为
\(\begin{aligned} \text { minimize } \quad& f_{0}(x)\\ \text { s.t. } \quad& f_{i}(x) \leq 0, \quad i=1, \ldots, m\\ &h_{i}(x)=0, \quad i=1, \ldots, p \end{aligned} \\\)
其中 \(f_0(x)\) 为目标函数,\(f_i(x)\) 为不等式约束函数, \(h_i\) 为等式约束函数。优化问题的最优解为
\(p^{\star}=\inf \left\{f_{0}(x) | f_{i}(x) \leq 0, i=1, \ldots, m, h_{i}(x)=0, i=1, \ldots, p\right\} \\\)
注:\(p^*\) 使用 \(\inf\) 函数的原因是因为,最优解可能是趋近一个值。
如果 \(p^*=\infty\),则问题不可行;如果 \(p^*=-\infty\) 则该问题没有下界。
最优解则有 \(f_0(x)=p^*\),局部最优解(local optimal)有
\(\begin{aligned} \text{minimize} (\text{over } z) \quad& f_{0}(z) \\ \text{s.t.} \quad&f_{i}(z) \leq 0, \quad i=1, \ldots, m, \quad h_{i}(z)=0, \quad i=1, \ldots, p \\ &\|z-x\|_{2} \leq R \end{aligned} \\\)
也即只在一个小的邻域内考虑优化问题。
注意:
- 有的优化问题有最小值,但是没有可行解,比如 \(f_0(x)=1/x\);
- 有的问题根本就没有最小值,比如 \(f_0(x)=-\log x\)
- 有的问题只有局部最小值,比如 \(f_0(x)=x^3-3x\)
上面提到的优化问题中有等式和不等式约束,这些我们都称为显式约束(explicit constraints)
同时由于 \(x\) 应属于各个函数的定义域内,因此还有隐式约束(implicit constraint),即
\(x \in \mathcal{D}=\bigcap_{i=0}^{m} \operatorname{dom} f_{i} \cap \bigcap_{i=1}^{p} \operatorname{dom} h_{i} \\\)
注:隐式约束其实就是目标函数 \(f_0\) 的定义域,不要忽视了上述 \(\mathcal{D}\) 包含了 \(f_0\) 的定义域
没有显式约束的优化问题被称为无约束优化问题(unconstrained)。比如
\(\text { minimize } \quad f_{0}(x)=-\sum_{i=1}^{k} \log \left(b_{i}-a_{i}^{T} x\right) \\\)
是一个无约束优化问题,包含了隐式约束 \(a_i^Tx< b_i\)。
其实有约束优化问题也可以转化为无约束优化问题,只需要加一个指示函数,一开始提到的一般优化问题就可以利用 \(\delta_C\) 转化为下面的无约束优化问题,不过这种转化可能并没有太大的意义
\(\min_x f_0(x)+\delta_{C}(x) \\ \delta_C(x)=\begin{cases}0&f_i(x)\le0,h_i(x)=0 \\ \infty \end{cases} \\\)
注:上述的约束优化问题转化为无约束优化问题,在未来约束优化算法的时候可能会用到
除了优化问题,还有一种可行解问题(Feasibility problem),也就是给定一系列约束来寻找是否有可行解
\(\begin{aligned} \text {find} \quad& x \\ \text { s.t.} \quad& f_{i}(x) \leq 0,\quad i=1, \ldots, m \\ & h_{i}(x)=0,\quad i=1, \ldots, p \end{aligned} \\\)
这实际上也可以转化为一般优化问题
\(\begin{aligned} \text {minimize} \quad& 0 \\ \text { s.t.} \quad& f_{i}(x) \leq 0,\quad i=1, \ldots, m \\ & h_{i}(x)=0,\quad i=1, \ldots, p \end{aligned} \\\)
注:可行解问题,就是寻找一个可行域,也就是所有可行解的集合
二、凸优化问题
2.1 凸优化问题定义
注:凸优化问题和普通优化问题的区别就是对目标函数和约束条件做了各种限
凸优化问题(Convex optimization problem)要求目标函数为凸函数,而且定义域为凸集,这样可以利用凸函数和凸集的优良性质简化问题,因此凸优化问题的一般形式为
\(\begin{aligned} \text { minimize } \quad& f_{0}(x)\\ \text { s.t. } \quad& f_{i}(x) \leq 0, \quad i=1, \ldots, m\\ &Ax=b, \qquad\qquad\qquad\qquad\quad\bigstar \end{aligned} \\\)
其中要求目标函数和约束函数 \(f_0,f_1,...,f_m\) 均为凸函数。
Remarks:需要注意这里还要求等式约束均为仿射函数,这是因为我们希望定义域是凸集,假设等式约束 \(h_i\) 不是线性的,即使 \(h_i\) 是凸函数,\(\{x|h_i(x)=0\}\) 也不一定是凸集。比如二次等式约束 \(\Vert x\Vert_2=r\),得到的定义域就是一个球面,显然不是一个凸集,这对优化不利。
有时候我们直接拿到的优化问题并不符合上面的形式,但是可以经过化简得到等价问题,就是凸的了,比如
\(\begin{aligned} \text { minimize } \quad& f_{0}(x)=x_{1}^{2}+x_{2}^{2}\\ \text { s.t. } \quad& f_{1}(x)=x_{1} /\left(1+x_{2}^{2}\right) \leq 0\\ &h_{1}(x)=\left(x_{1}+x_{2}\right)^{2}=0 \end{aligned} \\\)
经过简单化简就有
\(\begin{aligned} \text { minimize } \quad& x_{1}^{2}+x_{2}^{2}\\ \text { s.t. } \quad& x_{1} \leq 0\\ &x_{1}+x_{2}=0 \end{aligned} \\\)
2.2 凸优化问题的最优解
对于凸优化问题有一个极其重要的性质,就是
凸优化问题的局部最优解就是全局最优解
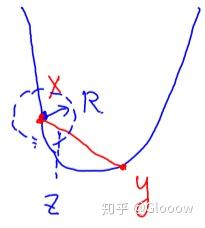
证明也很简单,若 \(x^*\) 为局部最优解,只需要假设另外一个全局最优解 \(y\ne x^*,f(y)\) ,那么利用凸函数的性质,就可以在 \(x^*\) 的邻域内导出矛盾,如下图图示。
凸优化问题的最优解还有一个很好的判据
\(x\) 为最优解,当且仅当
\(\nabla f_{0}(x)^{T}(y-x) \geq 0 \quad \text { for all feasible } y \\\)证明过程只需要应用凸函数的一阶等价定义即可,即 \(f(y)\ge f(x)+\nabla f^T(x)(y-x)\)。
这个怎么直观理解呢?还记得我们之前在拟凸函数那里提到的“支撑超平面”吗?实际上 \(f_0(x)\) 定义了一个等高线,由于 \(f_0\) 是一个凸函数,因此这个等高线实际上围成了一个凸集,这个凸集也就是一个下水平集。而这里的 \(\nabla f_0(x)\) 就是这个下水平集的一个支撑超平面,正如下图所示。同时注意,\(\nabla f_0(x)\) 也代表着函数指上升的方向,如果说对任意定义域内的 \(y\),都有 \(\nabla f_{0}(x)^{T}(y-x) \geq 0\) 成立,那么说明我们从 \(x\) 走到 \(y\) 总会使 \(f_0\) 增大,也就是说 \(x\) 就是最优解,对应最小值。
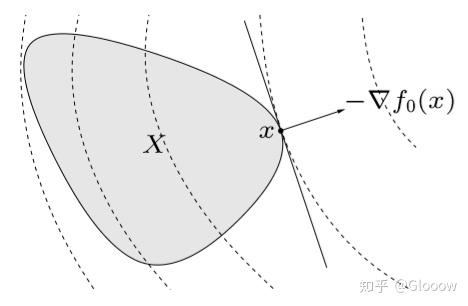
注:其实还可以从内积的角度考虑,由于 \(\nabla f_0(x)\) 和 \(y-x\) 两者形成钝角,也就是说 \(y-x\) 一定在 \(f_0(x)\) 形成的等高线和 \(\nabla f_0(x)\) 形成的支撑超平面之内,如果在之外,那么内积就会 \(\leq 0\),也就会形成一个钝角
利用上面这两个性质,我们可以对很多类型的凸优化问题的最优解有一个认识。
无约束优化问题:对无约束优化问题,\(x\) 为最优解,当且仅当
\(x\in\text{dom} f_0,\quad \nabla f_0(x)=0 \\\)
等式约束优化问题:\(\min\quad f_0(x),\qquad s.t.\quad Ax=b\),则有 \(x\) 为最优解,当且仅当存在 \(\nu \in \mathcal{N}(A)\)
\(x \in \operatorname{dom} f_{0}, \quad A x=b, \quad \nabla f_{0}(x)+A^{T} \nu=0 \\\)
证明:因为 \(Ax=b\) 实际上定义了一个超平面,如果 \(x\) 为最优解,那么 \(\nabla f_0(x)\) 一定没有这个平面内的分量,也就是说 \(\nabla f_0(x)\in \ker(A)^\perp\),也就是说 \({\nabla f_0(x) }^T \nu = 0\),再使用 KKT 条件,即可得到上述结果。
2.3 等价问题化简
有时原始优化问题比较难,可以通过等价转换进行简化。
消去等式约束:比如对一般的凸优化问题,等式约束实际上定义了一个超平面,这可以表示为特解 + 一组基的形式
\(Ax=b \iff x=Fz+x_0 \text { for some } z \\\)
原始凸优化问题就可转化为
\(\begin{aligned} \text { minimize (over }z) \quad& f_{0}\left(F z+x_{0}\right)\\ \text { s.t. } \quad& f_{i}\left(F z+x_{0}\right) \leq 0, \quad i=1, \dots, m \end{aligned} \\\)
添加等式约束:实际上就是上面的一个逆过程,这个过程中需要添加一个等式约束 \(y=Ax+b\),由于添加了变量 \(y\),会使问题变量数增加,同时优化变量也需要加上 \(y\)。
引入松弛变量:比如对于线性不等式约束的优化问题
\(\begin{aligned} \text { minimize } \quad& f_{0}(x)\\ \text { s.t. } \quad& a_i^Tx\le b_i,\quad i=1,...,m \end{aligned} \\\)
可以引入松弛因子 \(s_i\),得到
\(\begin{aligned} \text { minimize } \quad& f_{0}(x)\\ \text { s.t. } \quad& a_i^Tx + s_i = b_i,\quad i=1,...,m \\ & s_i \ge0,\quad i=1,...,m \end{aligned} \\\)
例子:下面两个优化问题是等价的吗?其中 \(W^TW=I\)
\(\min_x f(x)+g(Wx) \\ \min_c f(W^T c)+g(c) \\\)
不一定等价。由于 \(W^TW=I\),若 \(W\) 为方阵,则二者等价,否则说明 \(W\in R^{m\times n},m\ge n\),也即 \(W\) 为一个瘦高型的矩阵,如果我们取 \(f\equiv 0\),那么很显然 \(\min_x g(Wx)\) 与 \(\min_c g(c)\) 并不等价,因为 \(W\) 列不满秩。
epigraph 形式:任意标准形式的凸优化问题都可以转化为下面的形式
\(\begin{aligned} \text { minimize } \quad& t\\ \text { s.t. } \quad& f_{0}(x) -t \leq 0\\ \quad& f_{i}(x) \leq 0, \quad i=1, \ldots, m\\ &Ax=b \end{aligned} \\\)
这种变化很重要,可以将优化目标转化为约束函数,对于后面一些典型凸优化问题的转化很有用。
对某些变量最小化:实际上就是对于存在多个优化变量时,提前通过计算消去一些变量
\(\begin{aligned} \text { minimize } \quad& f_{0}\left(x_{1}, x_{2}\right)\\ \text { s.t. } \quad& f_{i}\left(x_{1}\right) \leq 0, \quad i=1, \dots, m \end{aligned} \iff \begin{aligned} \text { minimize } \quad& \tilde{f}_{0}\left(x_{1}\right)\\ \text { s.t. } \quad& \tilde{f}_{i}\left(x_{1}\right) \leq 0, \quad i=1, \dots, m \end{aligned} \\\)
其中 \(\tilde{f}_0(x_1)=\inf_{x_2}f_0(x_1,x_2)\)。
三、拟凸优化问题
拟凸函数跟凸函数有一些相似的性质,尤其是拟凸函数的任意下水平集都是凸集,因此很多时候对于拟凸问题,也可以用凸优化的一些方法有效解决。
拟凸优化问题(Quasi convex optimization) 的一般定义为与凸优化基本相同,只不过目标函数 \(f_0(x)\) 可以是拟凸函数,但约束函数 \(f_1,...,f_m\) 仍需要是凸函数。
Remarks:我个人觉得这里其实约束函数也可以是拟凸函数?因为即使是拟凸函数,\(f_i(x)\le0\) 也可以得到凸的定义域?
但是此时拟凸优化问题就没有凸优化那么好的性质了,比如局部最优解不一定是全局最优解
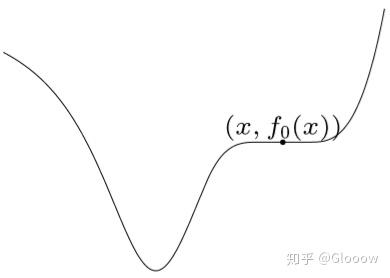
注:尽管如此,由于拟凸函数任意下水平集 \(\{x|f(x)\le t\}\) 都是凸集,我们可以利用这个性质将其转化为凸函数 \(\phi_t(x)\le0\) 来表示,由此就可以用凸优化来求解。
例子
最简单的例子,拟凸函数 \(f(x)\) 的下水平集可以表示为 \(\{x|f(x)\le t\}\),我们可以用函数 \(\phi_t(x)\le0\) 来等价表示
\(\phi_t(x)=\begin{cases}0 & f(x)\le t \\ \infty \end{cases} \\\)
不过这种表示方法意义不大, 这个函数不连续不可微。我们还有其他的表示方法比如
\(\phi_t(x)=\text{dist}\left(x,\{z|f(z)\le t\}\right) \\\)
另外,如果拟凸函数 \(f_0(x)\) 有一些特定的性质,比如 \(f_0(x)=p(x)/q(x)\),其中 \(p(x)\) 为凸函数,而 \(q(x)>0\) 为凹函数(容易证明此时 \(f_0\) 为拟凸函数),那么我们还可以取 \(\phi_t(x)\) 为
\(\phi_t(x)=p(x)-t q(x) \\\)
拟凸优化问题的求解
假如当前拟凸优化问题的最优解为 \(p^*\),那么对于寻找可行解问题
\(\begin{aligned} \text{find} \quad& x \\ s.t. \quad& \phi_{t}(x) \leq 0, \quad f_{i}(x) \leq 0, \quad i=1, \ldots, m, \\ &A x=b \end{aligned} \\\)
如果 \(p^* \leq t\),则该问题有可行解,如果 \(p^* \gt t\) ,则没有可行解。因此对于原始凸优化问题,可以利用二分法迭代求解

注:如果能找到 \(x\),表明问题存在可行解,由于 \(f_0(x) \leq t\) ,自然可以得出 \(p^* \leq t\),不存在可行解,则就是 \(f_0(x) \gt t\),则就是 $ p^* \gt t$
四、典型凸优化问题
4.1 线性规划(LP)
注:目标函数和约束函数都是线性的
线性规划(Linear program)问题的一般形式为
\(\begin{aligned} \text{minimize} \quad& c^{T} x+d \\ \text{s.t.} \quad& G x \preceq h \\ &A x=b \end{aligned} \\\)
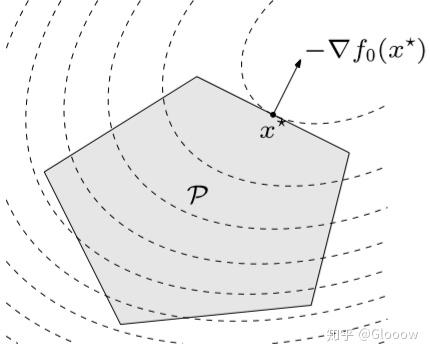
联系我们前面提到的凸优化问题最优解性质,有 \(c^T(y-x)\ge0\),也即目标函数的等高线是一系列超平面
例子 1:对于 piecewise-linear minimization 问题(无约束优化)
\(\text { minimize } \max _{i=1, \ldots, m}\left(a_{i}^{T} x+b_{i}\right) \\\)
可以转化为
\(\begin{aligned} \text { minimize} \quad& t\\ \text { s.t.} \quad& a_i^Tx + b_i \le t \end{aligned} \\\)
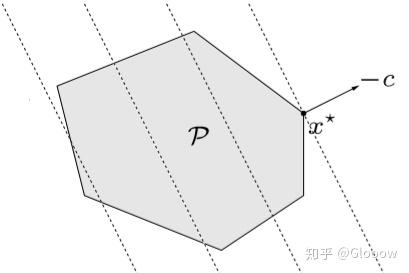
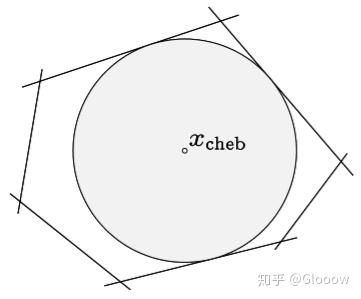
例子 2:多面体的切比雪夫中心(Chebyshev center)
\(\mathcal{P}=\left\{x | a_{i}^{T} x \leq b_{i}, i=1, \dots, m\right\} \\\)
可以用优化问题表示为
\(\begin{aligned} \text{maximize} \quad& r\\ \text{s.t.} \quad& a_{i}^{T} x_{c}+r\left\|a_{i}\right\|_{2} \leq b_{i}, \quad i=1, \ldots, m \end{aligned} \\\)
4.2 线性分式规划
注:目标函数是线性分式函数,约束函数是线性函数
线性分式规划(Linear-fractional program) 的一般形式为
\(\begin{aligned} \text{minimize} \quad& f_0(x) \\ \text{s.t.} \quad& G x \preceq h \\ &A x=b \end{aligned} \\\)
其中 \(f_0(x)=\frac{c^Tx+d}{e^Tx+f},\quad \text{dom}f_0(x)=\{x|e^Tx+f>0\}\)。这个问题可以等价转化为线性规划。
4.3 二次规划(QP)
注:目标函数是二次的,约束函数是线性的
二次规划(Quadratic program)的一般形式为
\(\begin{aligned} \text{minimize} \quad& (1/2)x^TPx+q^Tx+r \\ \text{s.t.} \quad& G x \preceq h \\ &A x=b \end{aligned} \\\)
其中 \(P\in S_{+}^n\)。
与线性规划不同的是,目标函数的等高线变成了椭球面
例子:最小二乘就是最经典的二次规划的例子,\(\min \Vert Ax+b\Vert_2^2\)
4.4 二次约束二次规划(QCQP)
注:目标函数和不等式约束函数都是二次的
二次约束二次规划(Quadratically constrained quadratic program)的一般形式为
\(\begin{aligned} \text{minimize} \quad& (1/2)x^TP_0x+q_0^Tx+r_0 \\ \text{s.t.} \quad& (1/2)x^TP_ix+q_i^Tx+r_i \le 0 \\ &A x=b\end{aligned} \\\)
其中 \(P_i\in S_{+}^n\)。
一般会限制 \(P_1,...,P_m\in S_{++}^n\),也就是不能为 0 矩阵(有什么意义吗?不关键)
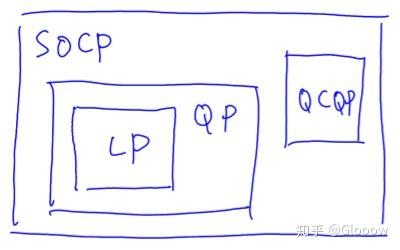
4.5 二次锥规划(SOCP)
注:不等式约束是二阶锥约束,也就是是一个二阶锥
二次锥规划(Second-order cone programming)的一般形式为
\(\begin{array}{cl} \text { minimize } & f^{T} x \\ \text { s.t. } & \left\|A_{i} x+b_{i}\right\|_{2} \leq c_{i}^{T} x+d_{i}, \quad i=1, \ldots, m \\ & F x=g \end{array} \\\)
其实 SOCP 比前面几种问题都更广泛,他们都可以看作是 SOCP 的一种情况
4.6 鲁棒线性规划
对于优化问题,有时候我们的参数比如 \(a_i,b_i\) 等都是不确定的,他们可能是在一定范围内属于某个集合,也可能是一个随机变量,这个时候就引入了鲁棒优化的概念。
注:鲁棒优化,其实就是对于不确定的参数 \(a_i\),我们要求对于 \(a_i\) 的所有可能值都考虑进去,再对问题进行转化,然后使其变成一个稳定的线性规划
对于线性规划问题来说,比如
\(\begin{aligned} \text{minimize} \quad& c^{T} x+d \\ \text{s.t.} \quad& a_i^Tx\le b_i \end{aligned} \\\)
一种是考虑确定性模型,也即
\(\begin{aligned} \text{minimize} \quad& c^{T} x+d \\ \text{s.t.} \quad& a_i^Tx\le b_i \text{ for all } a_i\in\mathcal{E}_i \end{aligned} \\\)
如果 \(\mathcal{E}_{i}=\left\{\bar{a}_{i}+P_{i} u |\|u\|_{2} \leq 1\right\}\) 是一个椭球,则该问题可以转化为一个 SOCP 问题
\(\begin{aligned} \text{maximize} \quad& c^Tx\\ \text{s.t.} \quad& \bar{a}_{i}^{T} x+\left\|P_{i}^Tx\right\|_{2} \leq b_{i}, \quad i=1, \ldots, m \end{aligned} \\\)
另一种是随机性模型,即
\(\begin{aligned} \text{minimize} \quad& c^{T} x \\ \text{s.t.} \quad& \operatorname{prob}\left(a_{i}^{T} x \leq b_{i}\right) \geq \eta, \quad i=1, \ldots, m \end{aligned} \\\)
假如 \(a_i\sim\mathcal{N}(\bar{a}_i,\Sigma_i)\) 服从高斯分布,则该问题同样可以转化为一个 SOCP 问题
\(\begin{aligned} \text{maximize} \quad& c^Tx\\ \text{s.t.} \quad& \bar{a}_{i}^{T} x+\Phi^{-1}(\eta)\left\|\Sigma_{i}^{1 / 2} x\right\|_{2} \leq b_{i}, \quad i=1, \ldots, m \end{aligned} \\\)
4.7 几何规划(GP)
首先定义单项式函数(monomial function) \(f(x)=cx_1^{a_1}x_2^{a_2}\cdots x_n^{a_n},\quad \text{dom}f=R_{++}^n\),其中 \(c>0,a_i\) 为任意实数;
正项式函数(posynomial function) \(f(x)=\sum_k c_k x_1^{a_{1k}} x_2^{a_{2k}}\cdots x_n^{a_{nk}},\quad \text{dom}f=R_{++}^n\)
注:正项式其实可以看成多项式,因为 \(x_i\) 的项式个数是不确定的
然后就可以定义几何规划(geometric program)了
\(\begin{aligned} \text{minimize} \quad& f_0(x) \\ \text{s.t.} \quad& f_i(x)\le 1,\quad i=1,...,m \\ &h_i(x)=1,\quad i=1,...,p \end{aligned} \\\)
其中 \(f_i\) 为正项式,\(h_i\) 为单项式。
首先说明,这个优化问题并不一定是凸的,因为 \(a_i\) 可以取任意实数,比如 \(a_i=1/2\) 就不是凸的。那么我们这里为什么要介绍这个问题呢?别急,一会稍微做一个变换我们就可以解决这个问题了。那还有一个问题,这种形式的函数有什么意义呢?为什么专门引入这样一种非凸优化问题呢?我们看这个单项式函数 \(cx_1^{a_1}x_2^{a_2}\cdots x_n^{a_n}\),像不像体积或者面积的表达式?这也是他被称为“几何规划”的原因吧。
好,现在我们怎么把这个非凸的问题转化为凸优化问题呢?加个 \(\log\) 就行啦!对单项式来说
\(\begin{aligned} \log f(x) &= \sum_i a_i \log x_i +\log c = a^Ty+b \\ f(x) &= e^{a^Ty+b} \end{aligned} \\\)
对多项式来说
\(\log f(x)=\log \left(\sum_i \exp(a_i^Ty+b_i)\right) \\\)
这么一来,取完对数后的问题就是凸的了,而且我们也知道 \(\log\) 是一个单射函数,原始优化问题就变成了
\(\begin{aligned} \text{minimize} \quad& \log \left(\sum_k \exp(a_{0k}^Ty+b_{0k})\right) \\ \text{s.t.} \quad& \log \left(\sum_k \exp(a_{ik}^Ty+b_{ik})\right)\le 0,\quad i=1,...,m \\ &Gy+d=0 \end{aligned} \\\)
注:其实绝大多数情况看到连乘,都可以想到 \(\log\) 函数
4.8 半正定规划(SDP)
注:半正定规划的不等式约束是定义在凸锥上的,其他的和普通的凸优化问题极其相似
前面所讲到的都是标量函数,约束条件也都是函数值与 0 比大小,而前面的章节中我们也提到了广义不等式,对于正常锥则可以定义不等号。所以我们可以定义一种凸优化问题,这种凸优化问题的约束条件不再是普通不等式,而是广义不等式
\(\begin{aligned} \text{minimize} \quad& f_0(x) \\ \text{s.t.} \quad& f_i(x)\preceq_{K_i} 0,\quad i=1,...,m \\ &Ax=b \end{aligned} \\\)
其中 \(f_0:R^n\to R\) 为凸函数,\(f_i:R^n\to R^{k_i}\) 为关于正常锥 \(K_i\) 的凸函数。
注意这种带有广义不等式约束的凸优化问题与普通凸优化问题有着相同的性质,比如可行集为凸的,局部最优解就是全局最优解等。
一种简单形式的凸优化问题就是向量形式的,也就是说目标函数与约束都是仿射函数
\(\begin{aligned} \text{minimize} \quad& c^Tx \\ \text{s.t.} \quad& Fx+g\preceq_K 0 \\ &Ax=b \end{aligned} \\\)
这种向量形式的广义不等式实际上就是对每个元素进行比较,因此实际上可以按照每一行拆分成多个不等式,如果取 \(K=R_+^m\) 就与普通的线性规划(LP)没什么区别了。
接下来要介绍的就是重头戏半正定规划(Semidefinite program)了,我们取 \(K=S^n_+\)
\(\begin{aligned} \text{minimize} \quad& c^Tx \\ \text{s.t.} \quad& x_1 F_1+x_2F_2+\cdots+x_nF_n+G\preceq_K 0 \\ &Ax=b \end{aligned} \\\)
其中 \(F_i,G\in S^n\)。
这里的不等式约束就是大名鼎鼎的线性矩阵不等式(linear matrix inequality, LMI)。
如果说我们现在有两个不等式约束怎么办呢?
\(x_1 \hat{F}_1+x_2\hat{F}_2+\cdots+x_n\hat{F}_n+G\preceq_K 0 \\ x_1 \tilde{F}_1+x_2\tilde{F}_2+\cdots+x_n\tilde{F}_n+G\preceq_K 0 \\\)
合成一个更大的矩阵就可以了,实际上这种操作在后面也会经常见到
\(x_{1}\left[\begin{array}{cc} \hat{F}_{1} & 0 \\ 0 & \tilde{F}_{1} \end{array}\right]+x_{2}\left[\begin{array}{cc} \hat{F}_{2} & 0 \\ 0 & \tilde{F}_{2} \end{array}\right]+\cdots+x_{n}\left[\begin{array}{cc} \hat{F}_{n} & 0 \\ 0 & \tilde{F}_{n} \end{array}\right]+\left[\begin{array}{cc} \hat{G} & 0 \\ 0 & \tilde{G} \end{array}\right] \preceq 0 \\\)
这是因为分块对角矩阵为正定矩阵等价于每一个子块都为正定矩阵。
例子 1:半正定规划之所以重要,是因为他的形式更广泛,前面说 SOCP 包含了 LP、QP、QCQP,而半正定规划则包含了 SOCP!比如下面的 SOCP 问题就可以转化为 SDP
\(\begin{aligned} SOCP:\qquad \text{minimize}&\quad f^{T} x \\ \text{s.t.}&\quad \left\|A_{i} x+b_{i}\right\|_{2} \leq c_{i}^{T} x+d_{i}, \quad i=1, \ldots, m \\ \\ SDP:\qquad \text{minimize}&\quad f^{T} x \\ \text{s.t.}&\quad \left[\begin{array}{cc} \left(c_{i}^{T} x+d_{i}\right) I & A_{i} x+b_{i} \\ \left(A_{i} x+b_{i}\right)^{T} & c_{i}^{T} x+d_{i} \end{array}\right] \succeq 0, \quad i=1, \ldots, m \end{aligned} \\\)
例子 2:最小化矩阵的最大特征值 \(\min \lambda_{\max}(A(x))\),也可以通过半正定规划来描述
\(\begin{aligned} \text{minimize} \quad& t \\ \text{s.t.} \quad& A(x)\preceq tI \end{aligned} \\\)
其中优化变量为 \(x\in R^n,t\in R\)。这种等价转化是因为 \(\lambda_{\max}(A)\le t\iff A\preceq tI\)。
例子 3:最小化矩阵范数 \(\min \Vert A(x)\Vert_2=\left(\lambda\left(A\left(x\right)^TA\left(x\right)\right)\right)^{1/2}\),也可以等价为SDP
\(\begin{aligned} \text{minimize}&\quad t \\ \text{s.t.}&\quad \left[\begin{array}{cc} t I & A(x) \\ A(x)^T & tI \end{array}\right] \succeq 0 \end{aligned} \\\)
五、向量优化
注:向量优化的函数都是基于锥定义的,也就是它完全是从一个高维的角度看待凸优化问题,因此在进行向量优化的时候,需要注意向量优化的可行解也是在锥上定义的,因此就最优解可能会出现两种结果,也就是最优解可能是一个集合 \(\mathcal{O}\),如果 \(f_0(x)\) 是关于锥的最小元,则称作最优解;如果 \(f_0(x)\) 是关于锥的极小元,则称为 Pareto optimal。
前面介绍的所有优化问题的目标函数都是标量(尽管约束可能会出现广义不等式),如果目标函数为向量怎么办呢?前面的章节中我们介绍了广义的凸函数,同样也是基于锥定义的(实际上高维空间中“比大小”我们一般都需要通过锥来定义)。
一般的向量优化问题可以表示为
\(\begin{alignat}{} &\text{minimize(w.r.t. K)} \quad& f_0(x) \\ &\text{s.t.} \quad& f_i(x)\le 0,\quad i=1,...,m \\ & &h_i(x)=0,\quad i=1,...,p \end{alignat} \\\)
凸的向量优化问题只需要将上面的等式约束换为仿射函数 \(Ax=b\),同时要求 \(f_0\) 为 \(K-\)convex 的,\(f_1,...,f_m\) 为凸的。
向量约束优化问题的最优解相当于在下面的集合中寻找最优解
\(\mathcal{O}=\{f_0(x)|x \text{ feasible}\} \\\)
前面在将广义不等式和凸集的时候,我们讲过最小元和极小元的概念,这两个概念是不是已经忘得差不多啦!反正我基本全忘了......让我们来复习一下。
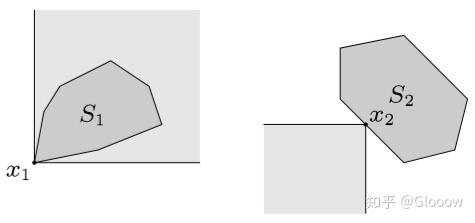
复习:最小元与极小元
下面两幅图分别表示最小元和极小元
利用对偶锥,我们可以获得最小元的等价定义,即
\(x\) 是集合 \(S\) 关于 \(\preceq_{K}\) 的最小元 \(\iff\) 对任意的 \(\lambda \succ_{K*} 0\),\(x\) 为 \(\lambda^Tz\) 在集合 \(S\) 上的唯一最小解
什么意思呢?也就是说任意的 \(\lambda\in K^*\),实际上都代表了一个法向量,也就是一个支撑超平面。如果 \(x\) 是最小元,则意味着对任意一个 (\(K^*\)所定义的) 支撑超平面来说,\(x\) 都是支撑点,就像下面这条幅图一样
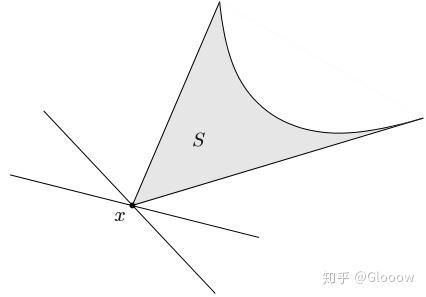
而极小元的定义是什么呢?
- 充分条件:若对于某些 \(\lambda \succ_{K*} 0\),\(x\) minimizes \(\lambda^Tz\) over \(S\),\(\Longrightarrow\)\(x\) 为极小元
- 必要条件:\(x\) 为凸集\(S\) 的极小元,\(\Longrightarrow\) 存在非 0 的 \(\lambda \succ_{K*} 0\) 使得 \(x\) minimizes \(\lambda^Tz\) over \(S\)
我们来看充分条件,只需要存在某一个 \(\lambda\in K^*\),使得 \(x\) 为对应支撑超平面的支撑点就可以了。比如下面这幅图,蓝色的点,我们可以找到这样一个蓝色的支撑超平面,使其为支撑点,所以它就是一个极小元;而对于红色的点来说,无论如何不可能找到一个支撑超平面,使其为支撑点,因此他就有可能不是极小元,因为这只是充分条件(对这个例子来说他就不是极小元)。
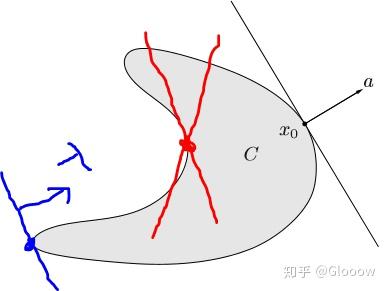
简单总结一下:
- 最小元:无论沿着锥 \(K^*\) 里边哪一个方向走,\(x\) 都是最小值点,那么他就是最小元;
- 极小元:如果沿着其中某一个方向走,\(x\) 是最小值点,那么他就是极小元。
复习完了最小元和极小元,不要忘了正事。我们要考虑向量约束优化问题中的最优解
\(\mathcal{O}=\{f_0(x)|x \text{ feasible}\} \\\)
这是一个集合,如果 \(f_0(x)\) 是关于锥 \(K\) 的最小元,那么对应的 \(x\) 就被称为最优解(optimal);如果 \(f_0(x)\) 是关于锥 \(K\) 的极小元,那么对应的 \(x\) 则被称为 Pareto optimal。
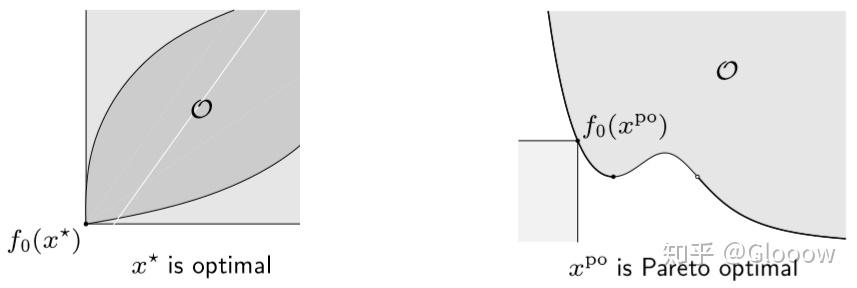
例子:假如我们取 \(K=R_+^q\),其中
\(f_0(x)=(F_1(x),...,F_q(x)) \\\)
相当于有 \(q\) 个不同的目标 \(F_i\),最好的情况当然是希望 \(F_i\) 都是最小的。
若 \(x^*\) 为最小元(存在)就说明任意其他可行解 \(y\) 都有 \(f_0(x^*)\le f(y)\),正是我们希望的;
而如果只能得到极小元 \(x^{po}\),就有对任意可行解 \(y\),\(f_0(y)\preceq f_0(x^{po})\Longrightarrow f_0(x^{po})=f(y)\)。这是什么意思呢?
- 首先不可能存在另一个 \(y\) 使得每一个元素都有 \(F_i(y)\le F_i(x^{po})\),要不然 \(x^{po}\) 出现在这里的意义是什么?我们直接选择 \(y\) 作为极小元不就好了吗?如果存在那也顶多是 \(F_i(y)=F_i(x^{po}),\forall i\),这种情况下 \(y\) 跟 \(x^{po}\) 其实没什么区别了。
- 第二点,有可能存在某些 \(y\),满足对一些 \(i\) 有 \(F_i(y)>F_i(x^{po})\),而对另一些 \(i\) 则有 \(F_i(y)<F_i(x^{po})\) ,这意味着 \(y\) 在某些方面表现得比 \(x^{po}\) 差,但在另一些方面则表现得更好,这实际上体现了我们在不同因素之间的一种权衡。
注:上面用数学术语抽象的讲了 Pareto optimal,很难理解。这里对 Pareto optimal 做一种现实意义的解释,由于绝大多数现实问题需要考虑很多的条件的,比如房价需要考虑价格、地区、环境等,那如果我们倾向于不同的考虑因素,则会形成不同的 Pareto optimal,毕竟现实问题是很难出现最优解的
参考文献:Stephen Boyd, Lieven Vandenberghe: Convex Optimization


 浙公网安备 33010602011771号
浙公网安备 33010602011771号