04-拉格朗日对偶问题和KKT条件
04-拉格朗日对偶问题和KKT条件
凸优化从入门到放弃完整教程地址:https://www.cnblogs.com/nickchen121/p/14900036.html
一、拉格朗日对偶函数
[题设] 考虑以下标准形式的优化问题:
\(\begin{aligned} \text{minimize} \quad & f_0(x) \\ \text{s.t.} \quad & f_i(x)\leq 0, i=1,...,m \\ &h_i(x)=0, i=1,...,p \end{aligned}\)
- 其中 \(x\in R^n\) ,设值域 \(D=\cap^m_{i=0}dom~f_i\cap^p_{i=1}dom~h_i\) 不为空。
- 最优值记为 \(p^*\) ,不假设这个问题是凸的。
- 拉格朗日对偶:通过添加约束的加权和来增广目标函数。
[拉格朗日函数] 定义拉格朗日函数 \(L: R^n\times R^m\times R^p\rightarrow R\) 为
注:大概知道拉格朗日函数的构造形式即可,下面在拉个朗日对偶问题中会详细叙述它的作用
\(L(x,\lambda,v)=f_0(x)+\sum^m_{i=1}\lambda_i f_i(x) +\sum^p_{i=1}v_ih_i(x).\)
- 值域: \(dom~L=D\times R^m \times R^p.\)
- 拉格朗日乘子:记 \(\lambda_i\) 是第 \(i\) 个不等式约束 \(f_i(x)\leq 0\) 的拉格朗日乘子; \(v_i\) 是第 \(i\) 个等式约束 \(h_i(x)=0\) 的拉格朗日乘子。
- 乘子向量:向量 \(\lambda\) 和 \(v\) 称为对偶变量,或该问题的拉格朗日乘子向量。
[拉格朗日对偶函数] 定义拉格朗日对偶函数(或对偶函数) \(g:R^m\times R^p\rightarrow R\) 为拉格朗日函数关于 \(x\) 取得的最小值:对于 \(\lambda\in R^m, v\in R^p\)
\(g(\lambda,v)=inf_{x\in D} L(x,\lambda,v)\)
注:上面为什么用 \(\inf\) 这个函数,因为解可能是趋向于一个值,而不是一个具体的值
- 如果关于 \(x\) 无下界,那么对偶函数取值 \(-\infty.\)
- 对偶函数是凹的:因为对偶函数是一组关于 \((\lambda,v)\) 的仿射函数的逐点下确界,所以即使题设是凸的,对偶函数也是凹的
[最优值的下界] 对偶函数给出最优值 \(p^*\) 的下界: \(g(\lambda,v)\leq p^*\) , \(\forall \lambda\succeq 0, \forall v.\)
二、拉格朗日对偶问题
[拉格朗日对偶问题] 拉格朗日函数能给出的最好下界:
\(\begin{aligned} \text{maxmize} \quad &g(\lambda,v) \\ \text{s.t.} \quad & \lambda\succeq 0 \end{aligned}\)
注:这里解释下为什么要这样构造拉格朗日对偶问题,首先明确拉格朗日函数的作用:因为约束条件对定义域有着很大的限制,因此通过拉格朗日函数的形式去除优化问题的约束条件,取消约束限制对定义域的限制,让优化问题更容易求解,那为什么这样做有用呢?
我们可以这样来看拉格朗日函数 \(L(x,\lambda,v)=f_0(x)+\sum^m_{i=1}\lambda_i f_i(x) +\sum^p_{i=1}v_ih_i(x).\) ,其中由于约束条件 \(h_i(x)=0\) 进而 \(\sum^p_{i=1}v_ih_i(x) = 0\),并且如果 \(\lambda_i \geq 0\) 且 \(f_i(x)\leq 0\) 进而 $\sum^m_{i=1}\lambda_i f_i(x) \leq 0 $,也就是说 \(L(x,\lambda,v) \leq f_0(x)\)。
原问题是去寻找 \(f_0(x)\) 的最小值,那么通过上述的分析,我们是不是可以找到 \(L(x,\lambda,v)\) 的最小值去作为 \(f_0(x)\) 的最小值呢?可以的,只不过稍微有点误差而已,但是我们却轻松地解决了带约束问题的优化问题。
为此,为了减小这个误差,我们进而又想找到 \(L(x,\lambda,v)\) 的最小值中的最大值,也就有了 \(g(\lambda,v)\),最重要的还是,无论原问题是否为凸问题,\(g(\lambda,v)\) 都是一个凹函数。
- 上述称为拉格朗日对偶问题,也称原问题(primal problem)。
- 对偶可行:满足 \(\lambda\succeq 0\) , \(g(\lambda,v)>-\infty\) 称为对偶可行的。
- 对偶最优解(最优拉格朗日乘子):记 \((\lambda^*,v^*)\) 为对偶问题的最优解。
- 拉格朗日对偶问题是凸优化问题:因为目标函数是凹函数,约束集合是凸集。
另一方面,由于不论原函数是否为凸优化问题,新的问题都是凸的,因此可以方便求解。下面举几个例子。
[例子 1]:原问题为
\(\begin{aligned} \text { minimize } \quad& x^Tx\\ \text { s.t. } \quad& Ax=b \end{aligned} \\\)
那么可以很容易得到拉格朗日函数为 \(L(x,\nu)=x^Tx+\nu^T(Ax-b)\),对偶函数为 \(g(\nu)=-(1/4)\nu^TAA^T\nu-b^T\nu\),也即
\(p^\star\ge g(\nu)\)。
[例子 2]:标准形式的线性规划(LP)
\(\begin{aligned} \text { minimize } \quad& c^Tx\\ \text { s.t. } \quad& Ax=b,\quad x\succeq0 \end{aligned} \\\)
按照定义容易得到对偶问题为
\(\begin{aligned} \text { maximize } \quad& -b^T\nu\\ \text { s.t. } \quad& A^T\nu+c\succeq0 \end{aligned} \\\)
[例子 3]:原问题为最小化范数
\(\begin{aligned} \text { minimize } \quad& \Vert x\Vert\\ \text { s.t. } \quad& Ax=b \end{aligned} \\\)
对偶函数为
\(g(\nu)=\inf_{x} (\Vert x\Vert+\nu^T(b-Ax)) =\begin{cases}b^T\nu & \Vert A^T\nu\Vert_* \le1 \\ -\infty & o.w.\end{cases} \\\)
这个推导过程中用到了共轭函数的知识。实际上上面三个例子都是线性等式约束,这种情况下,我们应用定义推导过程中可以很容易联想到共轭函数。(实际上加上线性不等式约束也可以)
[例子 4]:(原问题非凸)考虑 Two-way partitioning (不知道怎么翻译了...)
\(\begin{aligned} \text { minimize } \quad& x^TWx\\ \text { s.t. } \quad& x_i^2=1,\quad i=1,...,n \end{aligned} \\\)
对偶函数为
\(\begin{aligned} g(\nu)=\inf_{x}\left( x^{T}(W+\operatorname{diag}(\nu)) x \right)-\mathbf{1}^{T} \nu =\left\{\begin{array}{ll} -\mathbf{1}^{T} \nu & W+\operatorname{diag}(\nu) \succeq 0 \\ -\infty & \text { otherwise } \end{array}\right. \end{aligned} \\\)
于是可以给出原问题最优解的下界为 \(p^\star\ge-\mathbf{1}^{T} \nu\) if \(W+\operatorname{diag}(\nu) \succeq 0\)。这个下界是不平凡的,比如可以取 \(\nu=-\lambda_{\min}(W)\mathbf{1}\),可以给出 \(p^\star\ge n\lambda_{\min}(W)\)。
注:弱强对偶的区别,简单点说,就是我们从对偶函数 \(g(\lambda,v)\) 找到的最大值是否为原函数 \(f_0(x)\) 的最优解,也就是通过对偶问题求解之后,对偶问题的解和真实问题的解有没有误差
[弱对偶性] 对偶问题的最优值记为 \(d^{*}\) , 是从对偶函数中得到的 \(p^{*}\) 的最优下界,因此不等式
\(d^{*}\leq p^{*}\) 成立即使最初问题不是凸的。这个性质称为弱对偶性。
- 最优对偶间隙: \(p^{*}-d^{*}\)
[强对偶性] 如果等式 \(d^{*}=p^{*}\) 成立,即最优对偶间隙为零,那么强对偶性成立。注:如果原问题为凸优化问题,一般情况下都成立。
- 强对偶性成立的条件:约束准则(constraint qualifications)
[Slater's constraint qualifications(SCQ)条件] 存在 \(x\in relint~D\) (relint指相对内部)使得 \(f_i(x)<0, i=1,...,m\) , \(Ax=b.\)
注:Slater 条件,如果简单说,就是看 \(f_i(x) \lt 0\) 是否严格满足
- 这样的点称为严格可行点。
- Slater定理说明如果Slater 条件成立(且原始问题是凸问题),那么强对偶性成立。
- 由于存在线性等式约束,因此实际定义域可能不存在内点,可以将这一条件放松为相对内点 \(x\in\text{relint}\mathcal{D}\);
- 如果不等式约束中存在线性不等式,那么他也不必严格小于0。也即如果 \(f_i(x)=C^Tx+d\),则只需要满足 \(f_i(x)\le0\) 即可。
三、强弱对偶的几何解释
[弱对偶性] 令集合 \(\mathcal{G}\) 是目标函数和约束函数的值的集合
注:看下面图片去理解的时候,需要注意,图片的阴影面积是目标函数和约束函数的值的集合,是一个集合,然后通过下面的叙述,就是从集合中找到一个支撑超平面,然后注意一些限制条件,比如\(u\preceq 0\), 就可以看出\(p^*\) 为什么是在那里了
\(\mathcal{G}=\{(f_1(x),...,f_m(x),h_1(x),...,h_p(x),f_0(x) )\in R^m\times R^p\times R| x\in D\}\)
\(p^{*}=inf\{t| (u,v,t)\in \mathcal{G},u\preceq 0, v=0 \}\)
为了得到关于 \((\lambda,\mathcal{v})\) 的对偶函数,我们最小化仿射函数: \((u,v,t)\in \mathcal{G},\)
\((\lambda,\mathcal{v},1)^T(u,v,t)=\sum^m_{i=1}\lambda_i u_i +\sum^p_{i=1}\mathcal{v}_iv_i+t\)
即对偶函数为:
\(g(\lambda,\mathcal{v})=inf\{(\lambda,\mathcal{v},1)^T(u,v,t)|(u,v,t)\in \mathcal{G}\}\)
如果下确界是有限的,那么
\((\lambda,\mathcal{v},1)^T(u,v,t)\geq g(\lambda,\mathcal{v})\)
这定义了一个 \(\mathcal{G}\) 的支撑超平面(以 \((\lambda,\mathcal{v},1)\) 为法向量且与 \(\mathcal{G}\) 在下方相切)。它是非垂直的。
假设 \(\lambda\succeq 0\) ,如果 \(u\preceq 0\) 且 \(v=0\) ,那么 \(t\geq (\lambda,\mathcal{v},1)^T(u,v,t).\) 因此,
\(p^*\geq g(\lambda,\mathcal{v}).\)
即得到了弱对偶性。
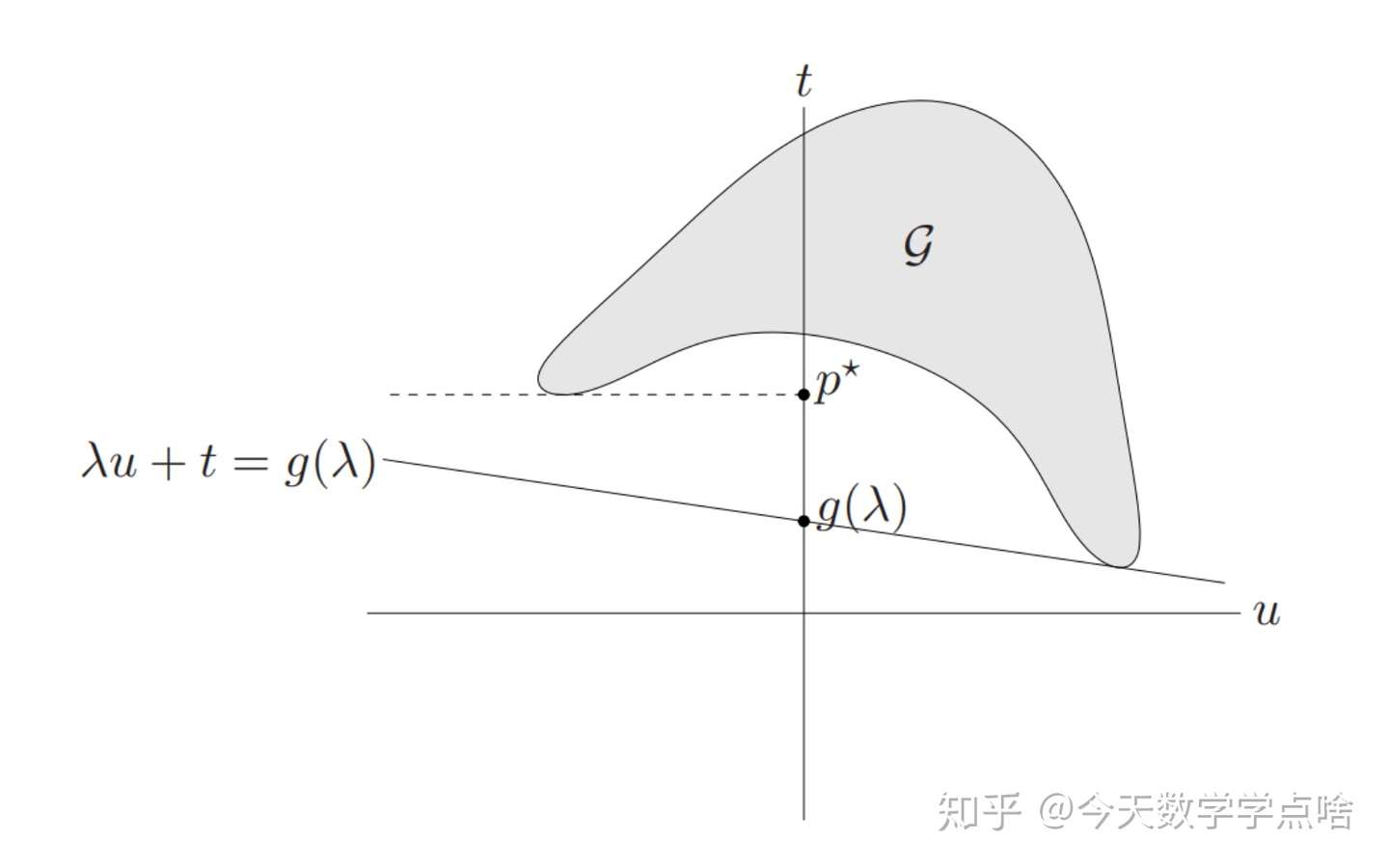
- 如图1,对于 \(\mathcal{G}=\{(f_1(x),f_0(x))|x\in D\}\) ,给定一个 \(\lambda\) ,然后在 \(\mathcal{G}\) 范围内最小化 \((\lambda,1)^T(u,t)\) ,得到一个斜率为 \(-\lambda\) 的支撑超平面 \(t=-\lambda u+g(\lambda)\) , \(g(\lambda)\) 位于 \(p^{*}\) 的下方。注:由于 \(g(\lambda) = t + \lambda u\),可以得知 \(g(\lambda)\) 就是 \(t\) 轴的交点,也就相当于截距。
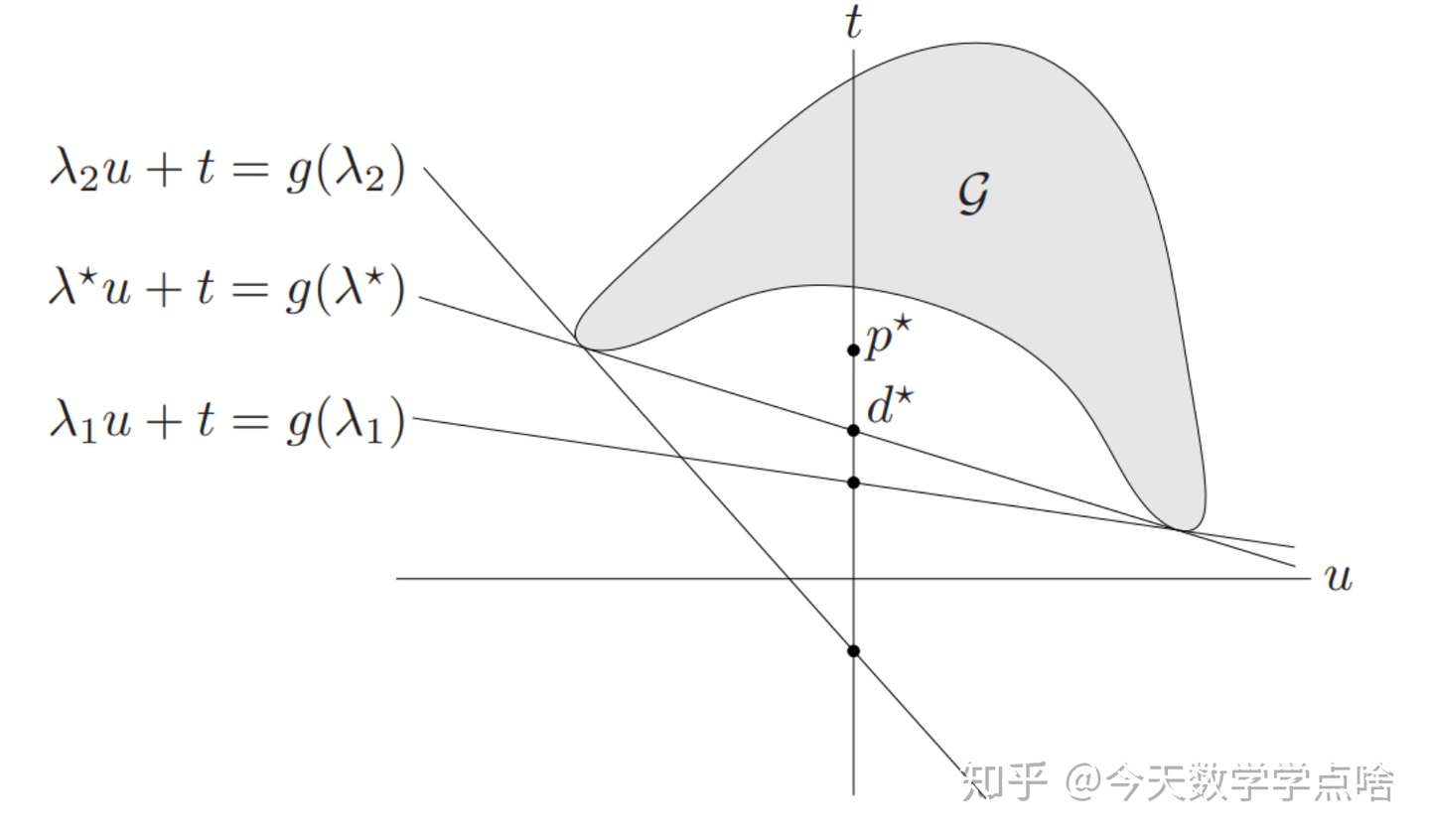
- 为了最大化 \(g(\lambda)\) ,给 \(\lambda\) 取不同的值, 如图2,即使是最优的 \(\lambda^{*}\) ,给出的 \(d^{*}\) 也在 \(p^{*}\) 的下方,所以不满足强对偶性,只有弱对偶性。注:可以把这看成是一个迭代的过程
注:再次讲讲 \(p^*\) 的来源,那么 \(p^\star\) 体现在哪个点呢?由于对于原优化问题,我们有 \(f_1(x)\le0\),因此体现在这个图里面就是 \(u\le0\),也就是上面左图当中的红色区域,而 \(p^\star=\min f_0(x)=\min t\)。
[弱对偶性的证明]:我们有 \(\lambda\ge0\)
\(\begin{aligned} p^\star &= \inf\{t|(u,v,t)\in\mathcal{G},u\le0,v=0\} \\ &\ge \inf\{t+\lambda^Tu+\mu^Tv|(u,v,t)\in\mathcal{G},u\le0,v=0\} \\ &\ge \inf\{t+\lambda^Tu+\mu^Tv|(u,v,t)\in\mathcal{G}\} \\ &= g(\lambda,\mu) \end{aligned} \\\)
[强对偶性条件 Slater’s constraint qualification(SCQ) 的证明]:由 \(g(\lambda,\mu)=\inf_{(u,v,t)\in\mathcal{G}}(t+\lambda^T u+\mu^Tv)\) 可以得到
\((\lambda,\mu,1)^T(u,v,t)\ge g(\lambda,\mu),\quad \forall (u,v,t)\in\mathcal{G} \\\)
这实际上定义了 \(\mathcal{G}\) 的一个超平面。特别的有 \((0,0,p^\star)\in\text{bd}\mathcal{G}\),因此也有
\((\lambda,\mu,1)^T(0,0,p^\star)\ge g(\lambda,\mu) \\\)
这个不等式可以自然地导出弱对偶性,当“=”成立时则可以导出强对偶性。那么什么时候取等号呢?点 \((0,0,p^\star)\) 为支撑点的时候!也就是说
如果在边界点 \((0,0,p^\star)\) 处存在一个非竖直的支撑超平面,那么我们就可以找到 \(\lambda,\mu\) 使得上面的等号成立,也就是得到了强对偶性。
注意前面的分析中我们并没有提到 SCQ,那么 SCQ 是如何保证强对偶性的呢?注意 SCQ 要求存在 \(x\in\mathcal{D}\) 使得 \(f(x)<0\),这也就意味着 \(\mathcal{G}\) 在 \(u< 0\) 半平面上有点,因此如果支撑超平面存在的话,就一定不是垂直的。
但这又引出另一个问题,那就是支撑超平面一定存在吗?答案是一定存在,这是由原问题的凸性质决定的。为了证明这一点,我们可以引入一个类似于 epigraph 的概念:
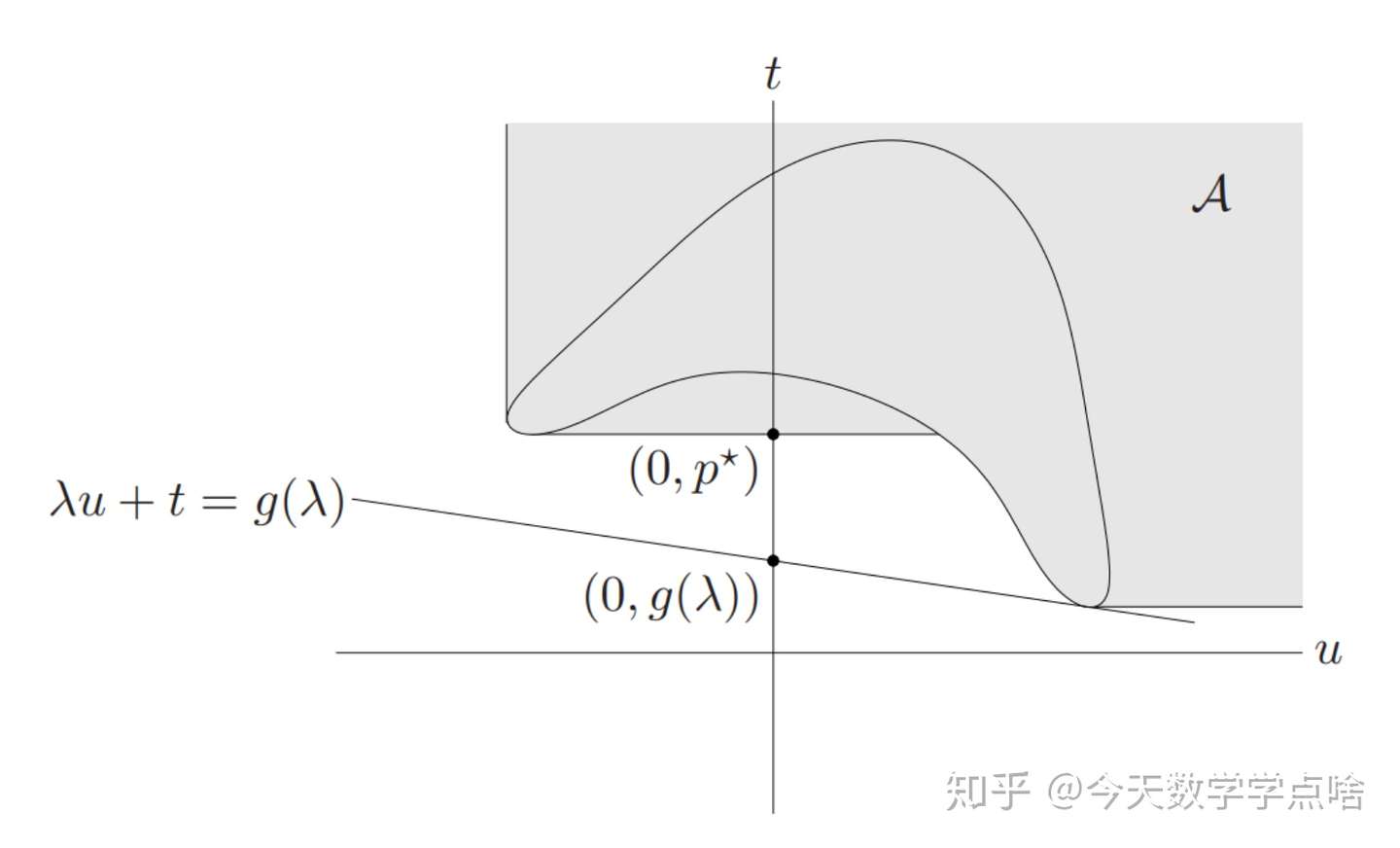
\(\begin{aligned} \mathcal{A} &= \mathcal{G} + (R^m_+\times \{0\}\times R_+) \\ &= \left\{(u,v,t) |\ \exists x\in\mathcal{D},s.t. f(x)\le u,h(x)=v,f_0(x)\le t\right\} \end{aligned} \\\)
由于原优化问题为凸的,可以应用定义证明集合 \(\mathcal{A}\) 也是凸的,同时 \((0,0,p^\star)\in\text{bd}\mathcal{A}\),那么集合 \(\mathcal{A}\) 在 \((0,0,p^\star)\) 点就一定存在一个支撑超平面。又由 SCQ 可知这个支撑超平面一定不是竖直的,因此就可以得到强对偶性了。
注:\((\lambda,\mu,1)^T(u,v,t)\ge g(\lambda,\mu),\quad \forall (u,v,t)\in\mathcal{A}\) 也成立。
注:说实话,这里我也有点半知半解,数学公式看的太乱了,反正要注意,\(u\) 相当于 \(f_i(x)\),\(v\) 相当于 \(h_i(x)\)。我只能说说我浅显的理解,就是从图中看,确保坐标轴 \(u\) 的负半轴有一个支撑超平面,且这个支撑超平面不是垂直的,那么 \(p^* \geq d^*\) 就被保证了。
四、鞍点解释
4.1 鞍点的基础定义
[鞍点定义]:一个不是局部最小值的驻点(一阶导数为0的点)称为鞍点。注:鞍点的数学含义是——目标函数在此点上的梯度(一阶导数)值为 0, 但从该点出发的一个方向是函数的极大值点,而在另一个方向是函数的极小值点。
[判断鞍点的一个充分条件]:函数在一阶导数为零处(驻点)的黑塞矩阵为不定矩阵(特征值有正有负的矩阵为不定矩阵)。
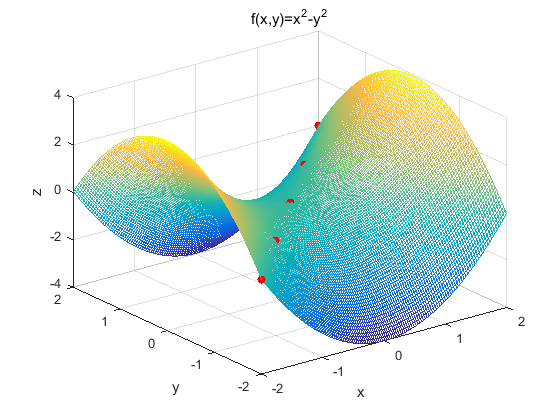
下面对函数 \(z=x^2-y^2\) 的驻点 \((0,0)\) 判断是否为鞍点。函数图像如下(红点为图像的鞍点):
我们根据定义来判断 \((0,0)\) 点的 Hessian 矩阵:
我们容易求得二元函数 \(z=x^2−y^2\) 在驻点 $ (0,0) $ 处的 Hessian 矩阵形式为:
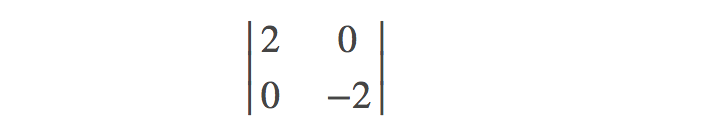
容易解出特征值一个为 \(2\),一个为 \(-2\)(有正有负),显然是不定矩阵,所以该点是鞍点。
注:函数在一阶导数为零处(驻点)的 Hessian 矩阵为不定矩阵只是判断该点是否为鞍点的充分条件,也就是说函数在一阶导数为零处(驻点)的 Hessian 矩阵不满足不定矩阵的定义,也不一定能够说明它不是鞍点。比如在 \(z=x^4−y^4\) 点 $ (0,0)$ 处的 Hessian 矩阵是一个 0 矩阵,并不满足是不定矩阵,但是它是一个鞍点。
4.2 极大极小不等式和鞍点性质
[极大极小不等式]:对任意 \(f\) :\(R^n × R^m \rightarrow R,\quad W \subseteq R^n Z \subseteq R^m\),有
对于上述这个不等式一般称为极大极小不等式。如果等式成立,即
则称 \(f\)(以及 \(W\) 和 \(Z\))满足强极大极小性质或者鞍点性质。
[鞍点性质]:注:这个解释更多的是为了下面讲述 KKT 条件,其实就是注意下这个强极大极小性质就是鞍点性质
我们称一对 \(\hat w \in W, \hat z \in Z\) 是函数 \(f\) (以及 \(W\) 和 \(Z\))的鞍点,如果对任意的 \(w \in W\) 和 \(z \in Z\) 下式成立:
也就是说,\(f(x,\hat z)\) 在 \(\hat w\) 处取得最小值(关于变量 \(w\in W\)),\(f(\hat w, z)\) 在 \(\hat z\) 处取得最大值(关于变量 \(z \in Z\)):
该式满足强极大极小性质,且共同值为 \(f(\hat w, \hat z)\),也就是上述说的,\(\hat w\) 和 \(\hat z\) 为 \(f\) 的鞍点。
五、最优性条件与 KKT 条件
5.1 KKT 条件
我们首先回顾一下拉格朗日函数,考虑下面的优化问题
\(\begin{aligned} \text { minimize } \quad& f_{0}(x)\\ \text { s.t. } \quad& f_{i}(x) \leq 0, \quad i=1, \ldots, m\\ &h_{i}(x)=0, \quad i=1, \ldots, p \end{aligned} \\\)
那么他的拉格朗日函数就是
\(L(x,\lambda,\nu)=f_0(x)+\lambda^Tf(x)+\nu^Th(x) \\\)
首先,我们看对偶函数
\(g(\lambda,\nu)=\inf_{x\in\mathcal{D}}\left(f_0(x)+\lambda^Tf(x)+\nu^Th(x)\right) \\\)
对偶问题实际上就是
\(d^\star = \sup_{\lambda,\nu}g(\lambda,\nu)=\sup_{\lambda,\nu}\inf_x L(x,\lambda,\nu) \\\)
然后我们再看原问题,由于 \(\lambda\succeq0,f(x)\preceq0\),我们有
\(f_0(x)=\sup_{\lambda,\nu}L(x,\lambda,\nu) \\\)
原问题的最优解实际上就是
\(p^\star=\inf_x f_0(x)= \inf_x \sup_{\lambda,\nu}L(x,\lambda,\nu) \\\)
弱对偶性 \(p^\star \ge d^\star\) 实际上说的是什么呢?就是 max-min 不等式
\(\inf_x \sup_{\lambda,\nu}L(x,\lambda,\nu) \ge \sup_{\lambda,\nu}\inf_x L(x,\lambda,\nu) \\\)
强对偶性说的又是什么呢?就是上面能够取等号
\(\inf_x \sup_{\lambda,\nu}L(x,\lambda,\nu) = \sup_{\lambda,\nu}\inf_x L(x,\lambda,\nu) = L({x}^\star,{\lambda}^\star,{\nu}^\star) \\\)
注:实际上 \({x}^\star,{\lambda}^\star,{\nu}^\star\) 就是拉格朗日函数的鞍点!!!(数学家们真实太聪明了!!!妙啊!!!)那么也就是说强对偶性成立等价于拉格朗日函数存在鞍点(在定义域内)。
好,如果存在鞍点(一阶导为 0)的话,我们怎么求解呢?还是看上面取等的式子
\(\begin{aligned} f_0({x}^\star) = g(\lambda^\star,\nu^\star) &= \inf_x \left( f_0(x)+\lambda^{\star T}f(x)+\nu^{\star T}h(x) \right) \\ & \le f_0(x^\star)+\lambda^{\star T}f(x^\star)+\nu^{\star T}h(x^\star) \\ & \le f_0(x^\star) \end{aligned} \\\)
这两个不等号必须要取到等号,而第一个不等号取等条件应为(鞍点一阶导为 0)
\(\nabla_x \left( f_0(x)+\lambda^{\star T}f(x)+\nu^{\star T}h(x) \right) =0 \\\)
第二个不等号取等条件为(这个条件成立,等号才能取到)
\(\lambda^\star_i f_i(x^\star)=0,\forall i \\\)
同时,由于 \({x}^\star,{\lambda}^\star,{\nu}^\star\) 还必须位于定义域内,需要满足约束条件,因此上面的几个条件共同构成了 KKT 条件。
KKT 条件
- 原始约束 \(f_i(x)\le0,i=1,...,m, \quad h_i(x)=0,i=1,...,p\)
- 对偶约束 \(\lambda\succeq0\)
- 互补性条件(complementary slackness) \(\lambda_i f_i(x)=0,i=1,...,m\)
- 梯度条件
\(\nabla f_{0}(x)+\sum_{i=1}^{m} \lambda_{i} \nabla f_{i}(x)+\sum_{i=1}^{p} \nu_{i} \nabla h_{i}(x)=0 \\\)
5.2 KKT 条件与凸问题
Remarks(重要结论)
- 前面推导没有任何凸函数的假设,因此不论是否为凸问题,如果满足强对偶性,那么最优解一定满足 KKT 条件。
- 但是反过来不一定成立,也即 KKT 条件的解不一定是最优解,因为如果 \(L(x,\lambda^\star,\nu^\star)\) 不是凸的,那么 \(\nabla_x L=0\) 并不能保证 \(g(\lambda^\star,\nu^\star)=\inf_x L(x,\lambda^\star,\nu^\star)\ne L(x^\star,\lambda^\star,\nu^\star)\),也即不能保证 \({x}^\star,{\lambda}^\star,{\nu}^\star\) 就是鞍点。
但是如果我们假设原问题为凸问题的话,那么 \(L(x,\lambda^\star,\nu^\star)\) 就是一个凸函数,由梯度条件 \(\nabla_x L=0\) 我们就能得到 \(g(\lambda^\star,\nu^\star)=L(x^\star,\lambda^\star,\nu^\star)=\inf_x L(x,\lambda^\star,\nu^\star)\),另一方面根据互补性条件我们有此时 \(f_0(x^\star)=L(x^\star,\lambda^\star,\nu^\star)\),因此我们可以得到一个结论
Remarks(重要结论):
- 考虑原问题为凸的,那么若 KKT 条件有解 \(\tilde{x},\tilde{\lambda},\tilde{\nu}\),则原问题一定满足强对偶性,且他们就对应原问题和对偶问题的最优解。
- 但是需要注意的是,KKT 条件可能无解!此时就意味着原问题不满足强对偶性!
假如我们考虑上一节提到的 SCQ 条件,如果凸优化问题满足 SCQ 条件,则意味着强对偶性成立,则此时有结论
Remarks(重要结论):
如果 SCQ 满足,那么 \(x\) 为最优解当且仅当存在 \(\lambda,\nu\) 满足 KKT 条件!
[例子 1]:等式约束的二次优化问题 \(P\in S_+^n\)
\(\begin{aligned} \text { minimize } \quad& (1/2)x^TPx+q^Tx+r \\ \text { s.t. } \quad& Ax=b \end{aligned} \\\)
那么经过简单计算就可以得到 KKT 条件为
\(\left[\begin{array}{cc} P & A^{T} \\ A & 0 \end{array}\right]\left[\begin{array}{l} x^{\star} \\ \nu^{\star} \end{array}\right]=\left[\begin{array}{c} -q \\ b \end{array}\right] \\\)
5.3 互补松弛性
假设原问题和对偶问题的最优值都可以达到且相等。令 \(x^*\) 是原问题的最优解, \((\lambda^*, \nu^*)\) 是对偶问题的最优解。这表明,
\(\begin{align} f_0(x^*) &= g(\lambda^*, \nu^*) \\ & = \inf_{x} \Big(f_0(x) + \sum_{i=1}^m \lambda_i^* f_i(x) + \sum_{i=1}^p \nu_i^* h_i(x)\Big) \\ &\leq f_0(x^*) + \sum_{i=1}^m \lambda_i^* f_i(x^*) + \sum_{i=1}^p \nu_i^* h_i(x^*)\\ &\leq f_0(x^*) \end{align} \tag{8}\)
其中第一个等式是因为强对偶的定义,第二个等式是Lagrange函数的定义,第三个不等式是根据Lagrange函数关于 \(x\) 求下确界小于等于其在 \(x^*\) 处的值(请确保你理解这个不等式),最后一个不等式是因为 \(\lambda_i^* \ge0, f_i(x^*) \leq 0, i = 1, \cdots, m\) 以及 \(h_i(x^*) = 0, i =1, \cdots, p\) 。因此,在上面的式子链中,两个不等式取等号。
由于第三个不等式可以取等式,这里有一个重要的结论:
\(\sum_{i=1}^m \lambda_i^* f_i(x^*) = 0 \\\)
事实上,求和的每一项都非正,因此有:
\(\lambda_i^* f(x_i^*) = 0 \quad i = 1, \cdots, m \\\)
所以,
\(\lambda_i^* > 0 \Rightarrow f_i(x^*) = 0 \\ f_i(x_i^*) < 0 \Rightarrow \lambda_i^* = 0\)
注:这表明在最优点处,原问题的不等式起作用时,对于的Lagrange问题的对应的不等式不起作用,反之亦然。
六、扰动及灵敏度分析
6.1 扰动问题
注:扰动其实就是约束条件多了点限制
现在我们再回到原始问题
\(\begin{aligned} \text { minimize } \quad& f_{0}(x)\\ \text { s.t. } \quad& f_{i}(x) \leq 0, \quad i=1, \ldots, m\\ &h_{i}(x)=0, \quad i=1, \ldots, p \end{aligned} \\\)
我们引入了对偶函数 \(g(\lambda,\nu)\),那这两个参数 \(\lambda,\nu\) 有什么含义吗?假如我们把原问题放松一下
\(\begin{aligned} \text { minimize } \quad& f_{0}(x)\\ \text { s.t. } \quad& f_{i}(x) \leq u_i, \quad i=1, \ldots, m\\ &h_{i}(x)=v_i, \quad i=1, \ldots, p \end{aligned} \\\)
记最优解为 \(p^\star(u,v)=\min f_0(x)\),现在对偶问题变成了
\(\begin{aligned} \max \quad& g(\lambda,\nu)-u^T\lambda -v^T\nu\\ \text{s.t.} \quad& \lambda\succeq0 \end{aligned} \\\)
假如说原始对偶问题的最优解为 \(\lambda^\star,\nu^\star\),松弛后的对偶问题最优解为 \(\tilde{\lambda},\tilde{\nu}\),那么根据弱对偶性原理,有
\(\begin{aligned} p^\star(u,v) &\ge g(\tilde\lambda,\tilde\nu)-u^T\tilde\lambda -v^T\tilde\nu \\ &\ge g(\lambda^\star,\nu^\star)-u^{T}\lambda^\star -v^{T}\nu^\star \\ &= p^\star(0,0) - u^{T}\lambda^\star -v^{T}\nu^\star \end{aligned} \\\)
这像不像关于 \(u,v\) 的一阶近似?太像了!实际上,我们有
\(\lambda_{i}^{\star}=-\frac{\partial p^{\star}(0,0)}{\partial u_{i}}, \quad \nu_{i}^{\star}=-\frac{\partial p^{\star}(0,0)}{\partial v_{i}} \\\)
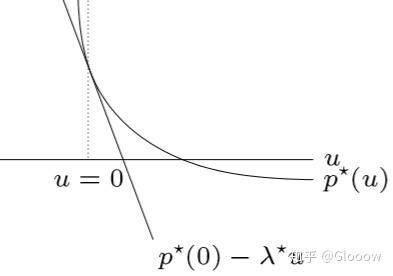
6.2 灵敏度分析
注:细节我也没认真看,其实看看下述给出的灵敏度解释,也就是大概知道扰动会对结果造成什么影响就行了
- 如果\(\lambda_i^*\)比较大,加强第i个约束,即\(u_i< 0\),则最优值\(P^*(u,l)\)会大幅增加。
- 如果\(\lambda_i^*\)比较小,放松第i个约束,即\(u_i> 0\),则最优值\(P^*(u,l)\)不会减小太多。
- 如果\(v_i^*\)比较大且大于0,\(l_i< 0]\),或者如果\(v_i^*\)比较大且小于0,\(l_i> 0\),则最优值\(P^*(u,l)\)会大幅增加。
- 如果\(v_i^*\)比较小且大于0,\(l_i> 0\),或者如果\(v_i^*\)比较大且小于0,\(l_i< 0\),则最优值\(P^*(u,l)\)不会减少太多。
七、Reformulation
前面将凸优化问题的时候,我们提到了Reformulation的几个方法来简化原始问题,比如消去等式约束,添加等式约束,添加松弛变量,epigraph等等。现在当我们学习了对偶问题,再来重新看一下这些方法。
7.1 引入等式约束
[例子 1】:考虑无约束优化问题 \(\min f(Ax+b)\),他的对偶问题跟原问题是一样的。如果我们引入等式约束,原问题和对偶问题变为
\(\begin{aligned} \text{minimize} \quad& f_{0}(y) \quad \\ \text{s.t.} \quad& A x+b-y=0 \end{aligned} \quad\qquad \begin{aligned} \text{minimize} \quad& b^{T} \nu-f_{0}^{*}(\nu) \\ \text{s.t.} \quad& A^{T} \nu=0 \end{aligned} \\\)
[例子 2]:考虑无约束优化 \(\min \Vert Ax-b\Vert\),类似的引入等式约束后,对偶问题变为
\(\begin{aligned} \text{minimize} \quad& b^{T} \nu \\ \text{s.t.} \quad& A^{T} \nu=0,\quad \Vert\nu\Vert_*\le1 \end{aligned} \\\)
7.2 显示约束与隐式约束的相互转化
[例子 3]:考虑原问题如下,可以看出来对偶问题非常复杂
\(\begin{aligned} \text{minimize} \quad& c^{T} x \\ \text{s.t.} \quad& A x=b \\ \quad& -1 \preceq x \preceq 1 \end{aligned} \begin{aligned} \text{maximize} \quad& -b^{T} \nu-\mathbf{1}^{T} \lambda_{1}-\mathbf{1}^{T} \lambda_{2} \\ \text{s.t.} \quad& c+A^{T} \nu+\lambda_{1}-\lambda_{2}=0 \\ \quad& \lambda_{1} \succeq 0, \quad \lambda_{2} \succeq 0 \end{aligned} \\\)
如果我们原问题的不等式约束条件转化为隐式约束,则有
\(\begin{aligned} \text{minimize} \quad& f_{0}(x)=\left\{\begin{array}{ll}c^{T} x & \Vert x\Vert_\infty \preceq 1 \\ \infty & \text { otherwise }\end{array}\right. \\ \text{s.t.} \quad& A x=b \end{aligned} \\\)
然后对偶问题就可以转化为无约束优化问题
\(\text{maximize} -b^T\nu-\Vert A^T\nu +c\Vert_1 \\\)
7.3 转化目标函数与约束函数
[例子 4]:还考虑上面提到的无约束优化问题 \(\min \Vert Ax-b\Vert\),我们可以把目标函数平方一下,得到
\(\begin{aligned} \text{minimize} \quad& (1/2)\Vert y\Vert^2 \\ \text{s.t.} \quad& Ax-b=y \end{aligned} \\\)
然后对偶问题就可以转化为
\(\begin{aligned} \text{minimize} \quad& (1/2)\Vert \nu\Vert_*^2+ b^T\nu \\ \text{s.t.} \quad& A^T\nu=0 \end{aligned} \\\)
参考文献:Stephen Boyd, Lieven Vandenberghe: Convex Optimization


 浙公网安备 33010602011771号
浙公网安备 33010602011771号