0604-转载-常用的神经网络层(详细)
0604-转载-常用的神经网络层(详细)
pytorch完整教程目录:https://www.cnblogs.com/nickchen121/p/14662511.html
一、写在前面
疫情在家的这段时间,想系统的学习一遍 Pytorch 基础知识,因为我发现虽然直接 Pytorch 实战上手比较快,但是关于一些内部的原理知识其实并不是太懂,这样学习起来感觉很不踏实,对 Pytorch 的使用依然是模模糊糊, 跟着人家的代码用 Pytorch 玩神经网络还行,也能读懂,但自己亲手做的时候,直接无从下手,啥也想不起来, 我觉得我这种情况就不是对于某个程序练得不熟了,而是对 Pytorch 本身在自己的脑海根本没有形成一个概念框架,不知道它内部运行原理和逻辑,所以自己写的时候没法形成一个代码逻辑,就无从下手。这种情况即使背过人家这个程序,那也只是某个程序而已,不能说会 Pytorch, 并且这种背程序的思想本身就很可怕, 所以我还是习惯学习知识先有框架(至少先知道有啥东西)然后再通过实战(各个东西具体咋用)来填充这个框架。而「这个系列的目的就是在脑海中先建一个 Pytorch 的基本框架出来, 学习知识,知其然,知其所以然才更有意思 」。
今天是该系列的第五篇文章, 通过上一篇内容我们已经知道了如何搭建模型并且也学习了关于搭建模型非常重要的一个类 nn.Module 和模型容器 Containers。搭建模型我们提到两个步骤,建立子模块和拼接子模块。而这次我们再细一点,具体学习几个重要的子模块,比如卷积层,池化层,激活函数,全连接层等。首先我们从卷积层开始, 学习一下 1/2/3 维度卷积,然后学习一下 nn.Conv2d 这个方法,最后介绍一下什么是转置卷积。然后我们进行池化层的学习,包括平均池化和最大池化,然后介绍一下全连接层,这个一般称为线性层, 最后我们介绍一些常用的非线性激活函数,为什么会用到非线性激活函数?一句话,没有非线性激活函数,再深的神经网络也没有“深度”的意义。这一篇文章中会见识到很多的动图,通过这些动图,可以更好的理解卷积,池化到底在做什么。
「大纲如下」:
- 卷积运算与卷积层(1/2/3d卷积,
nn.Conv2d, nn.ConvTranspose) - 池化运算与池化层(最大池化和平均池化)
- 全连接层
- 非线性激活函数层
- 总结梳理
下面是一张导图把知识拎起来:
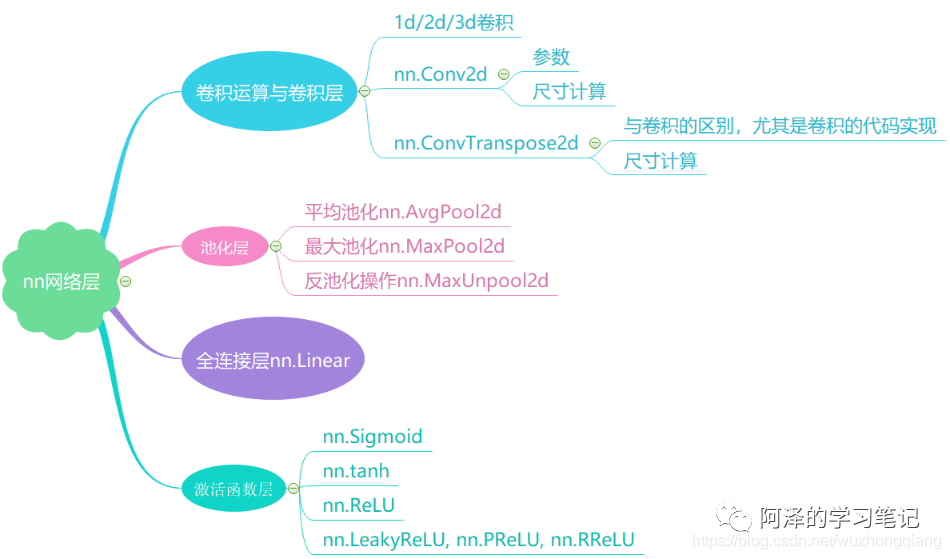
二、卷积运算与卷积层
说卷积层,我们得先从卷积运算开始,卷积运算就是卷积核在输入信号(图像)上滑动, 相应位置上进行「乘加」。卷积核又称为滤过器,过滤器,可认为是某种模式,某种特征。
卷积过程类似于用一个模板去图像上寻找与它相似的区域, 与卷积核模式越相似, 激活值越高, 从而实现特征提取。好吧,估计依然懵逼,下面我们就看看 1d、2d、3d的卷积示意图,通过动图的方式看看卷积操作到底在干啥?
2.1 1d 2d 3d 卷积示意
一般情况下,卷积核在几个维度上滑动,就是几维卷积。下面再看几张动图感受一下不同维度的卷积操作,注意下面都是一个卷积核:
一维卷积示意:
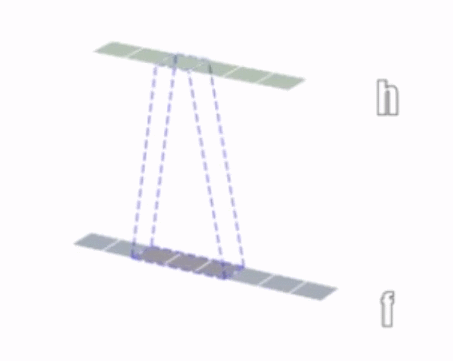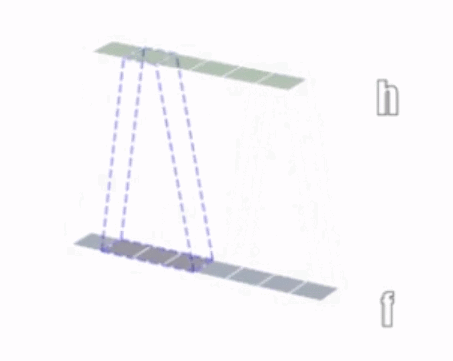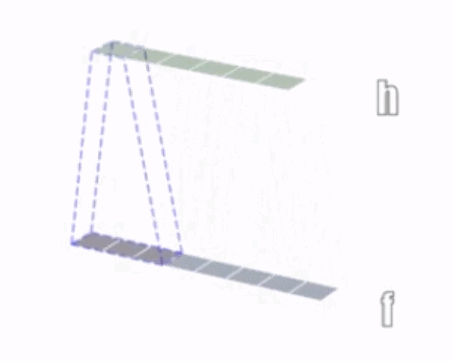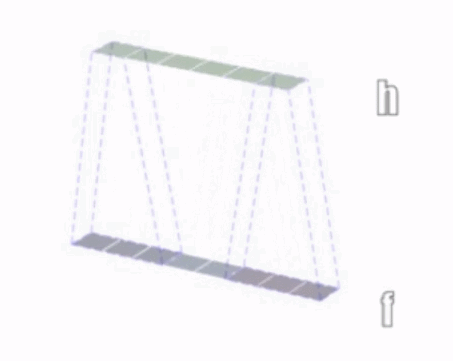
二维卷积示意:
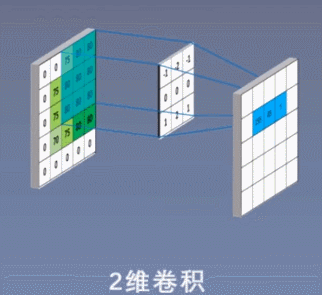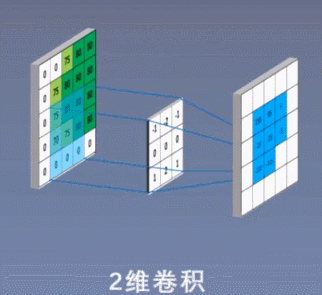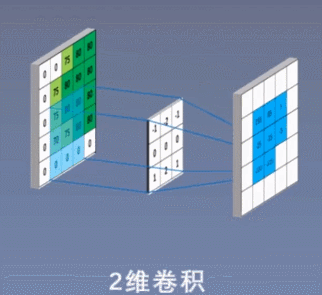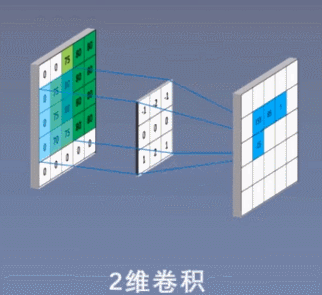
三维卷积示意:

2.2 nn.Conv2d
nn.Conv2d: 对多个二维信号进行二维卷积:

主要参数:
- in_channels: 输入通道数
- out_channels: 输出通道数, 等价于卷积核个数
- kernel_size: 卷积核尺寸, 这个代表着卷积核的大小
- stride: 步长, 这个指的卷积核滑动的时候,每一次滑动几个像素。下面看个动图来理解步长的概念:左边那个的步长是 1, 每一次滑动 1 个像素,而右边的步长是 2,会发现每一次滑动 2个像素。

- padding: 填充个数,通常用来保持输入和输出图像的一个尺寸的匹配,依然是一个动图展示,看左边那个图,这个是没有 padding 的卷积,输入图像是 4 * 4,经过卷积之后,输出图像就变成了 2 * 2 的了,这样分辨率会遍变低,并且我们会发现这种情况卷积的时候边缘部分的像素参与计算的机会比较少。所以加入考虑 padding 的填充方式,这个也比较简单,就是在原输入周围加入像素,这样就可以保证输出的图像尺寸分辨率和输入的一样,并且边缘部分的像素也受到同等的关注了。
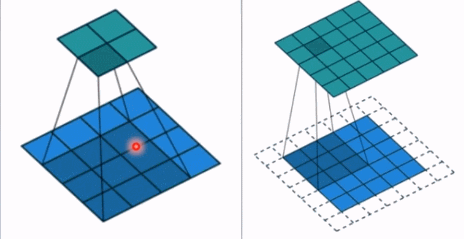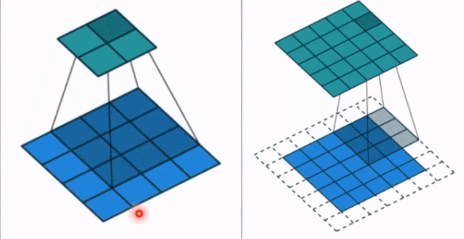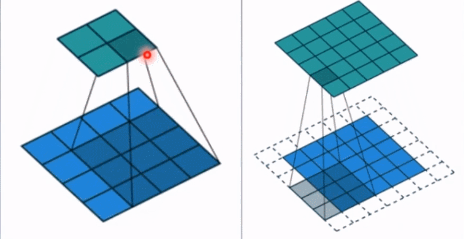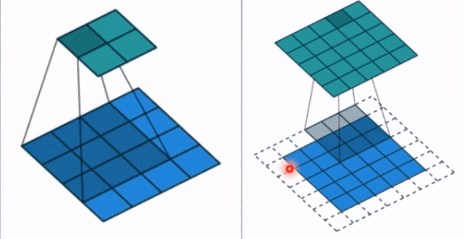
- dilation: 孔洞卷积大小,下面依然是一个动图:
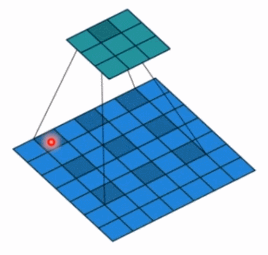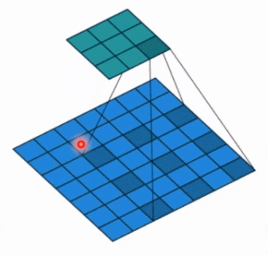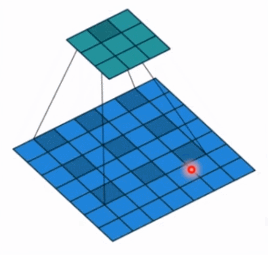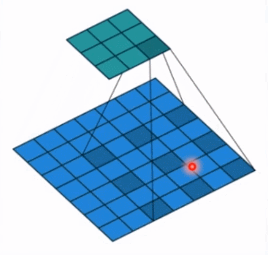
- 孔洞卷积就可以理解成一个带孔的卷积核,常用于图像分割任务,主要功能就是提高感受野。也就是输出图像的一个参数,能看到前面图像更大的一个区域。
- groups: 分组卷积设置,分组卷积常用于模型的轻量化。我们之前的 AlexNet 其实就可以看到分组的身影, 两组卷积分别进行提取,最后合并。
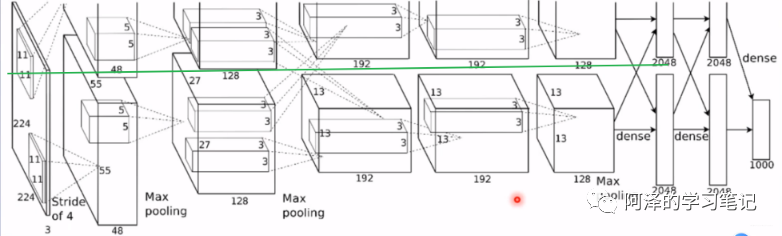
- bias: 偏置
下面是尺寸计算的方式:
- 没有 padding:\(out_{size}=\frac{In_{size}-kernel_{size}}{stride}+1\)
- 如果有 padding 的话:\(out_{size}=\frac{In_{size}+2*padding_{size}-kernel_{size}}{stride}+1\)
- 如果再加上孔洞卷积的话:\(out_{size}=\frac{In_{size}+2*padding_{size}+dilation_{size}*(kernel_{size}-1)-1}{stride}+1\)
下面我们用代码看看卷积核是怎么提取特征的,毕竟有图才有真相:
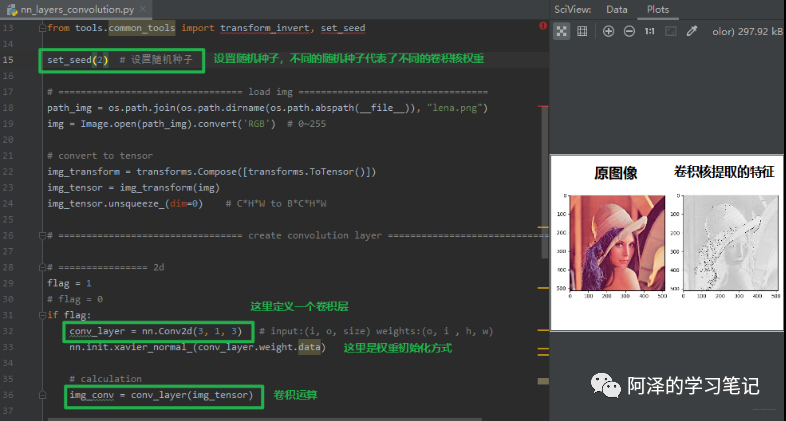
接下来,我们改变seed, 也就是相当于换一组卷积核, 看看提取到什么样的特征:

再换一个随机种子:
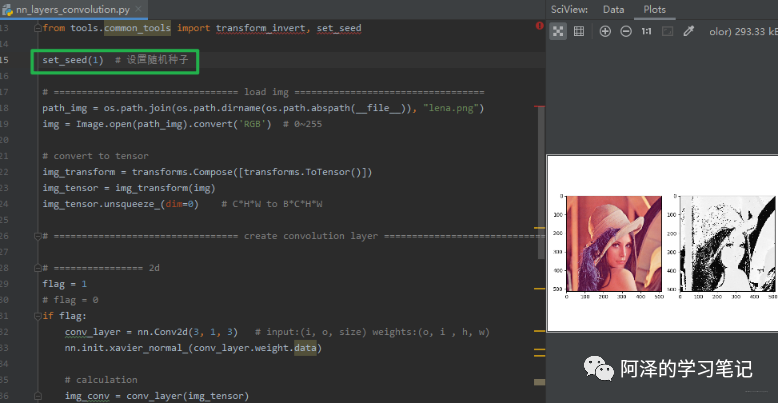
通过上面,我们会发现不同权重的卷积核代表不同的模式,会关注不同的特征,这样我们只要设置多个卷积核同时对图片的特征进行提取,就可以提取不同的特征。
下面我们看一下图像尺寸的变化:
卷积前尺寸:torch.Size([1, 3, 512, 512])
卷积后尺寸:torch.Size([1, 1, 510, 510])
卷积前,图像尺寸是 \(512*512\),卷积后,图像尺寸是 \(510*510\) 。我们这里的卷积核设置,输入通道 3,卷积核个数 1,卷积核大小 3,无 padding,步长是 1,那么我们根据上面的公式,输出尺寸:\((512-3)/1+1=510\)
下面再来看一下卷积层有哪些参数:我们知道卷积层也是继承于 nn.Module 的,所以肯定又是那 8 个字典属性, 我们主要看看它的_modules参数和_parameters参数字典。
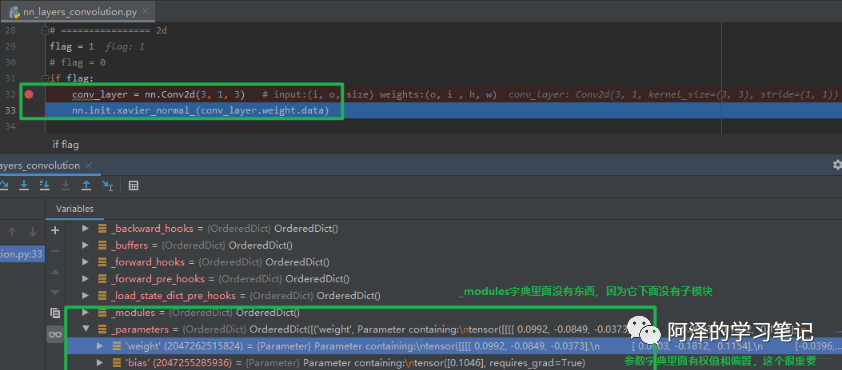
我们可以看到 Conv2d 下面的_parameters存放着权重参数,这里的 weight 的形状是 [1, 3, 3, 3], 这个应该怎么理解呢?首先 1 代表着卷积核的个数,第 1 个 3 表示的输入通道数,后面两个 3 是二维卷积核的尺寸。那么这里有人可能会有疑问,我们这里是3维的卷积核啊,怎么实现的二维卷积呢?下面再通过一个示意图看看:
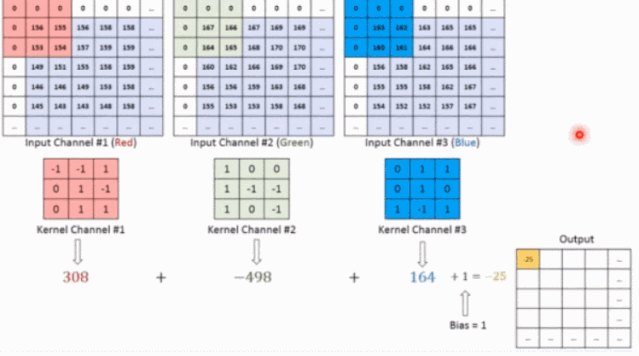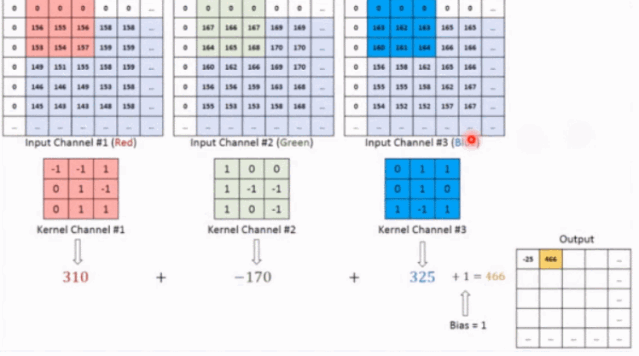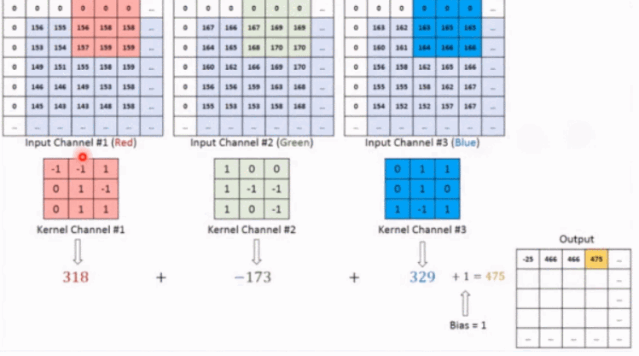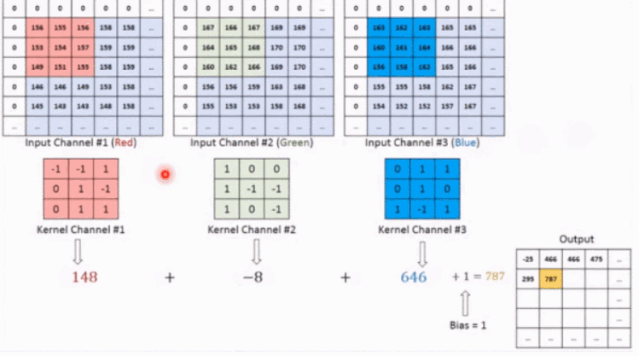
我们的图像是 RGB 3 个通道的图像,我们创建 3 个二维的卷积核,这 3 个二维的卷积核分别对应一个通道进行卷积,比如红色通道上,只有一个卷积核在上面滑动,每一次滑动,对应元素相乘然后相加得到一个数, 这三个卷积核滑动一次就会得到三个数,这三个数之和加上偏置才是我们的一个输出结果。这里我们看到了,一个卷积核只在 2 个维度上滑动,所以最后得到的就是 2 维卷积。这也能理解开始的卷积维度的概念了(一般情况下,卷积核在几个维度上滑动,就是几维卷积),为什么最后会得到的 3 维的张量呢?这是因为我们不止这一个卷积核啊,我们有多个卷积核的时候,每个卷积核都产生一个二维的结果,那么最后的输出不就成 3 维的了,第三个维度就是卷积核的个数了。下面用一个网站上的神图来看一下多个卷积核的提取特征,下面每一块扫描都是对应元素相乘再相加得到最后的的结果:

上面这一个是一个三维的卷积示意,并且使用了 2 个卷积核。最后会得到 2 个二维的张量。
二维卷积差不多说到这里吧,不明白我也没招了,我这已经浑身解数了,看这些动图也能看到吧,哈哈。毕竟这里主要讲 Pytorch,关于这些深度学习的基础这里不做过多的描述。下面再介绍一个转置卷积,看看这又是个啥?
2.3 转置卷积
转置卷积又称为反卷积和部分跨越卷积(当然转置卷积这个名字比逆卷积要好,原因在下面),用于对图像进行上采样。在图像分割任务中经常被使用。首先为什么它叫转置卷积呢?
在解释这个之前,我们得先来看看正常的卷积在代码实现过程中的一个具体操作:对于正常的卷积,我们需要实现大量的相乘相加操作,而这种乘加的方式恰好是矩阵乘法所擅长的。所以在代码实现的时候,通常会借助矩阵乘法快速的实现卷积操作, 那么这是怎么做的呢?
我们假设图像尺寸为 \(4*4\) ,卷积核为 \(3*3\) ,padding=0, stride=1,也就是下面这个图:

首先将图像尺寸的 \(4*4\) 拉长成 \(16*1\) ,16 代表所有的像素,1 代表只有 1 张图片。然后 \(3*3\) 的卷积核会变成一个 \(4*16\) 的一个矩阵,一脸懵逼了,这是怎么变的,首先这个 16,是先把 9 个权值拉成一列,然后下面补 7 个 0 变成16, 这个 4 是根据我们输出的尺寸计算的,根据输入尺寸,卷积核大小,padding, stride 信息可以得到输出尺寸是 \((4-3)/1+1=2\), 所以输出是 \(2*2\),那么拉成一列就是 4。这样我们的输出:\(O_{4*4}=K_{4*16}*I_{16*1}\)
这样就得到了最后一列输出 4 个元素,然后 reshape 就得到了 \(2*2\) 的一个输出特征图了。这就是用矩阵乘法输出一个二维卷积的这样一个示例。这就是那个过程:

下面我们看看转置卷积是怎么样的:
转置卷积是一个上采样,输入的图像尺寸是比较小的,经过转置卷积之后,会输出一个更大的图像,看下面示意图:

我们这里的输入图像尺寸是 \(2*2\), 卷积核为 \(3*3\), padding=0, stride=1,我们的输入图像尺寸是 \(4*4\),我们看看这个在代码中是怎么通过矩阵乘法进行实现的。首先,依然是把输入的尺寸进行拉长,成一个 \(4*1\) 的一个向量,然后我们的卷积核会变成 \(16*4\) 的,注意这里的卷积核尺寸,这个 4 依然是根据卷积核得来的,记得上面的那个 16 吗?我们是把卷积核拉长然后补 0, 在这里我们不是补 0 了,而是采用剔除的方法,因为我们根据上面的图像可以发现,虽然这里的卷积核有 9 个权值,可是能与图像相乘的最多只有四个(也就是卷积核在中间的时候),所以这里采用剔除的方法,从 9 个权值里面剔除 5 个,得到 4 个权重, 而这个 16,依然是根据输出图像的尺寸计算得来的。因为我们这里的输出是 \(4*4\), 这个可以用上面尺寸运算的逆公式。所以这里的输出:\(O_{16*1}=K_{16*4}*I_{4*1}\)
这次注意这个卷积核的尺寸是 \(16*4\),而我们正常卷积运算的卷积核尺寸 \(4*16\),所以在形状上这两个卷积操作卷积核恰恰是转置的关系,这也就是转置卷积的由来了。这是因为卷积核在转变成矩阵的时候,与正常卷积的卷积核形状上是互为转置,注意是形状,具体数值肯定是不一样的。所以正常卷积核转置卷积的关系并不是可逆的,故逆卷积这个名字不好。下面就具体学习 Pytorch 提供的转置卷积的方法:
nn.ConvTranspose2d: 转置卷积实现上采样

这个参数和卷积运算的参数差不多,就不再解释一遍了。
下面看看转置卷积的尺寸计算(卷积运算的尺寸逆):
- 无 padding:\(out_{size} = (in_{size}-1)*Stride+kerne_{size}\)
- 有 padding:\(out_{size} = (in_{size}-1)*Stride+kerne_{size}-2*padding_{size}\)
- 有 padding 和孔洞卷积:\(out_{size} = (in_{size}-1)*Stride+kerne_{size}-2*padding_{size}+(dilation_{size}-1)+1\)
下面从代码中看看转置卷积怎么用:
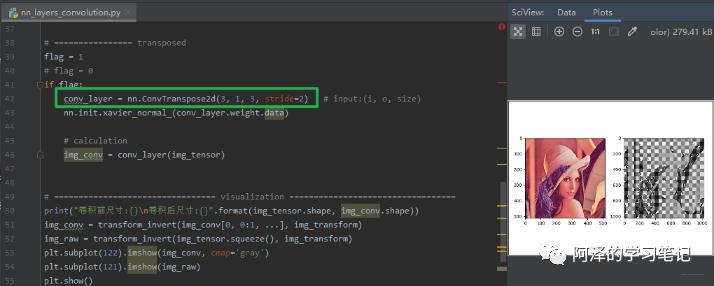
转置卷积有个通病叫做“棋盘效应”,看上面图,这是由于不均匀重叠导致的。至于如何解决,这里就不多说了。
关于尺寸变化:
卷积前尺寸:torch.Size([1, 3, 512, 512])
卷积后尺寸:torch.Size([1, 1, 1025, 1025])
我们发现,输入图像是 512 的,卷积核大小是 3,stride=2, 所以输出尺寸:\((512-1)*2+3=1025\)
简单梳理,卷积部分主要是卷积运算,卷积尺寸的计算,然后又学习了转置卷积。下面我们看看 nn 中其他常用的层。
三、池化层
池化运算:对信号进行“「收集」”并“「总结」”, 类似水池收集水资源, 因而美其名曰池化层。
- 收集:多变少,图像的尺寸由大变小
- 总结:最大值/平均值
下面是一个最大池化的动态图看一下(平均池化就是这些元素去平均值作为最终值):

最大池化就是这些元素里面去最大的值作为最终的结果。
下面看看 Pytorch 提供的最大池化和平均池化的函数——nn.MaxPool2d: 对二维信号(图像)进行最大值池化。

- kernel_size: 池化核尺寸
- stride: 步长
- padding: 填充个数
- dilation: 池化核间隔大小
- ceil_mode: 尺寸向上取整
- return_indices: 记录池化像素索引
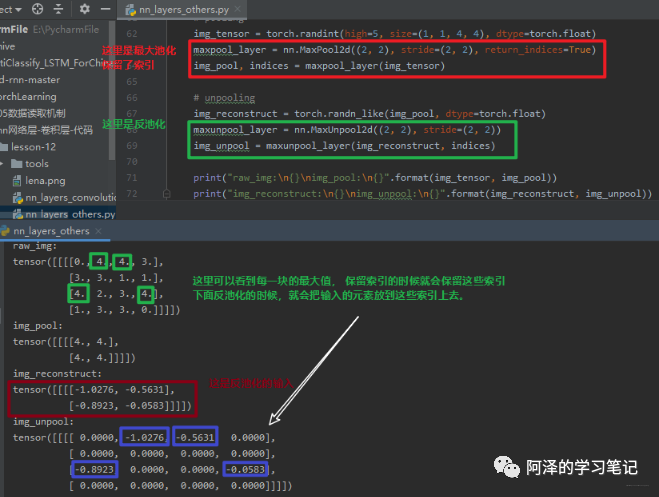
前四个参数和卷积的其实类似,最后一个参数常在最大值反池化的时候使用,那什么叫最大值反池化呢?看下图:
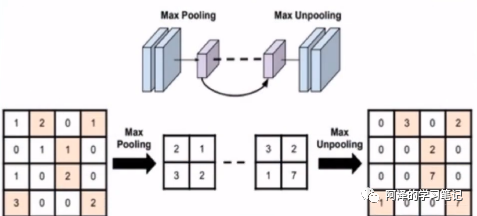
反池化就是将尺寸较小的图片通过上采样得到尺寸较大的图片,看右边那个,那是这些元素放到什么位置呢? 这时候就需要当时最大值池化记录的索引了。用来记录最大值池化时候元素的位置,然后在最大值反池化的时候把元素放回去。
下面看一下最大池化的效果:
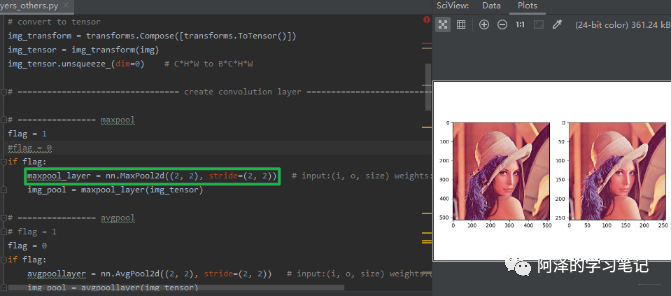
可以发现,图像基本上看不出什么差别,但是图像的尺寸减少了一半, 所以池化层是可以帮助我们剔除一些冗余像素的。
除了最大池化,还有一个叫做平均池化——nn.AvgPool2d: 对二维信号(图像)进行平均值池化

- count_include_pad: 填充值用于计算
- divisor_override: 除法因子, 这个是求平均的时候那个分母,默认是有几个数相加就除以几,当然也可以自己通过这个参数设定
下面也是通过代码看一下结果:
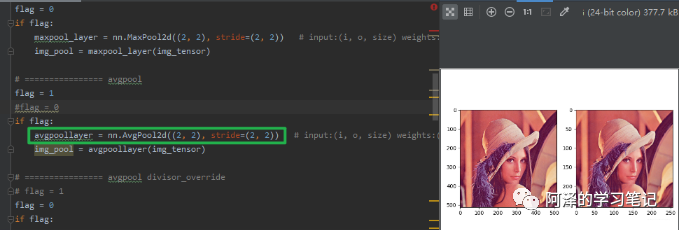
这个平均池化和最大池化在这上面好像看不出区别来,其实最大池化的亮度会稍微亮一些,毕竟它都是取的最大值,而平均池化是取平均值。
好了,这就是池化操作了,下面再整理一个反池化操作,就是上面提到的 nn.MaxUnpool2d: 这个的功能是对二维信号(图像)进行最大池化上采样

这里的参数与池化层是类似的。唯一的不同就是前向传播的时候我们需要传进一个 indices, 我们的索引值,要不然不知道把输入的元素放在输出的哪个位置上呀,就像上面的那张图片:

下面通过代码来看一下反池化操作:
四、线性层
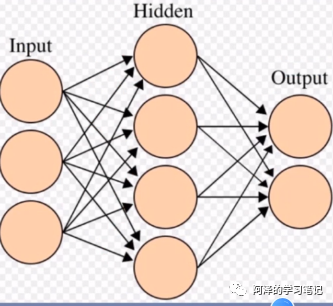
线性层又称为全连接层,其每个神经元与上一层所有神经元相连实现对前一层的「线性组合,线性变换」
线性层的具体计算过程在这里不再赘述,直接学习 Pytorch 的线性模块。
nn.Linear(in_features, out_features, bias=True) : 对一维信号(向量)进行线性组合
- in_features: 输入节点数
- out_features: 输出节点数
- bias: 是否需要偏置
计算公式:\(y=xW^T+bias\)
下面可以看代码实现:
inputs = torch.tensor([[1., 2, 3]])
linear_layer = nn.Linear(3, 4)
linear_layer.weight.data = torch.tensor([[1., 1., 1.], [2., 2., 2.],
[3., 3., 3.], [4., 4., 4.]])
linear_layer.bias.data.fill_(0.5)
output = linear_layer(inputs)
print(inputs, inputs.shape)
print(linear_layer.weight.data, linear_layer.weight.data.shape)
print(output, output.shape)
这个就比较简单了,不多说。
五、激活函数层
激活函数 Udine 特征进行非线性变换, 赋予多层神经网络具有「深度」的意义。
如果没有激活函数,我们可以看一下下面的计算:
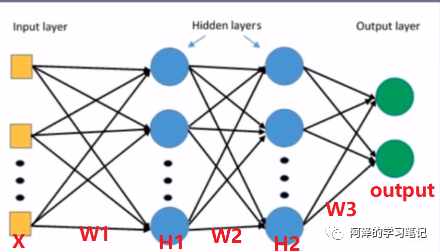
我们如果没有激活函数, 那么:
这里就可以看到,一个三层的全连接层,其实和一个线性层一样。这是因为我们线性运算的矩阵乘法的结合性,无论多少个线性层的叠加,其实就是矩阵的一个连乘,最后还是一个矩阵。所以如果没有激活函数,再深的网络也没有啥意义。
下面介绍几个常用的非线性激活函数:
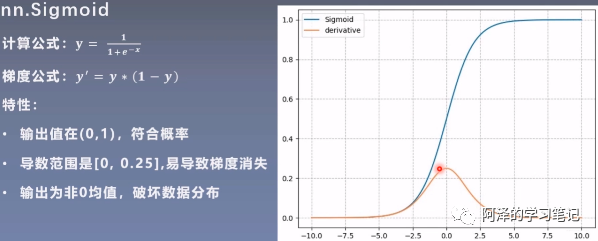
- sigmoid 函数:
-
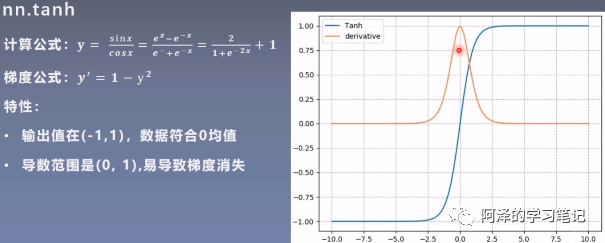
- nn.tanh:
-
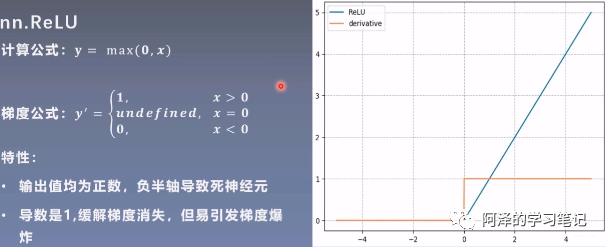
- nn.ReLU:
-
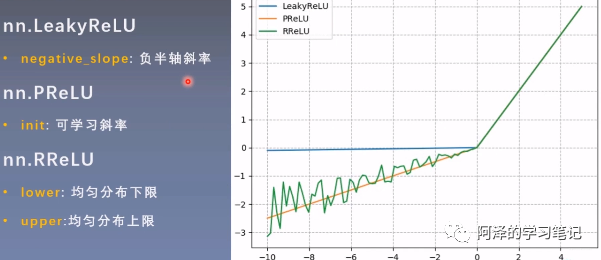
ReLU 相对于前面的两个,效果要好一些, 因为不容易造成梯度消失,但是依然存在问题,所以下面就是对ReLU 进行的改进。
六、总结
这篇文章的内容到这里就差不多了,这次以基础的内容为主,简单的梳理一下,首先我们上次知道了构建神经网络的两个步骤:搭建子模块和拼接子模块。而这次就是学习各个子模块的使用。从比较重要的卷积层开始,学习了1d 2d 3d 卷积到底在干什么事情,采用了动图的方式进行演示,卷积运算其实就是通过不同的卷积核去提取不同的特征。然后学习了 Pytorch 的二维卷积运算及转置卷积运算,并进行了对比和分析了代码上如何实现卷积操作。
第二块是池化运算和池化层的学习,关于池化,一般和卷积一块使用,目的是收集和合并卷积提取的特征,去除一些冗余,分为最大池化和平均池化。然后学习了全连接层,这个比较简单,不用多说,最后是非线性激活函数,比较常用的 sigmoid,tanh, relu等。
今天的内容就到这里,模型模块基本上到这里也差不多了,根据我们的那个步骤:数据模块 -> 模型模块 -> 损失函数 -> 优化器 -> 迭代训练。所以下一次开始学习损失函数模块,但是在学习损失函数之前,还得先看一下常用的权重初始化方法,这个对于模型来说也是非常重要的。所以下一次整理权值初始化和损失函数。
继续Rush 😉
参考书籍:《深度之眼——Pytorch》
所有代码链接:https://pan.baidu.com/s/1c5EYdd0w8j6w3g54KTxJJA 提取码:k7rh
本文分享自微信公众号 - 阿泽的学习笔记(aze_learning)
作者:Miracle8070
原文出处及转载信息见文内详细说明,如有侵权,请联系 nickchen121@163.com 删除。
原始发表时间:2020-08-29