0301-利用numpy解决线性回归问题

0301-利用numpy解决线性回归问题

目录

• 一、引言
• 二、线性回归简单介绍
  • 2.1 线性回归三要素
  • 2.2 损失函数
  • 2.3 梯度下降
• 三、解决线性回归问题的五个步骤
• 四、利用Numpy实战解决线性回归问题
• 五、总结

pytorch完整教程目录：https://www.cnblogs.com/nickchen121/p/14662511.html

一、引言

上一篇文章我们说到了torch和tf的功能，以及两者的区别。但是为了更好地去让大家体会框架的强大，我们首先不使用框架实现一个小demo。由于只是引入，因此，我们在这里使用一个比较简单的线性回归算法来讲解。

穿插一个广告，如果你对统计机器学习不是特别熟悉的话，建议你也简单看看，不说学会那些数学公式的推导，但是得知道那些算法是干啥的，我这里也有全套的视频和资料，链接在此：https://www.cnblogs.com/nickchen121/p/11686958.html

你都来学习框架了，接下来的所有内容我都默认你有一定的Python基础、数学基础、统计机器学习基础、深度学习基础，如果你有哪些不太会，我的博客里都有，可以自己去补一补，如果不喜欢我的，可以去bilibili找几个视频看，你都不喜欢？那就自己造一个出来。

二、线性回归简单介绍

2.1 线性回归三要素

由于现在统计机器学习一般也称为机器学习，但是真正的机器学习是包括是深度学习的，所以，接下来讲的机器学习这四个字你别太追究它原有的意义，大概知道是啥就行。

在机器学习中，我们知道，每一个算法简单点讲其实无非就是三个要素：一个输入、一个模型、一个输出，而线性回归属于机器学习算法，也是如此。输入就是一大堆的数据，输出就是我们想要的结果，而模型就是通过输入数据得出一个输出结果。举个例子吧。

现在我们这里有两组数据：

\[1.567 = w*x_1+b \\ 3.043 = w*x_2+b \]

这两组数据中，输入是\(x_1\)和\(x_2\)，模型就是一个函数\(f=y=w*x_i+b\)，输出就是\(1.567\)和\(3.043\)。知道这三个东西有什么用呢？有很大的用，我们可以看到我们这个函数有两个未知变量\(w\)和\(b\)，如果我们把这个输入看作是房子的面积，输出看成房子的价格，如果我们通过某种方法求出了\(w\)和\(b\)，我们就可以立即通过另外一个房子的面积\(x_3\)得知这个房子的价格。当然咯，实际情况不会这么简单，你别较真了。

那么问题来了，我们如何去求出\(w\)和\(b\)呢？有些耍些小聪明的同学马上会说到，这么简单地问题，我口算一下不就出来了嘛！\(w\approx{1.5}, b\approx{0.06}\)，然而这其实离精确求解差远了，如果这不是求解房价，而是求解股价的问题，那可就差之毫厘谬以千里了。

在这里重点声明一遍，我们举这么简单的例子只是为了让你明白使用框架和不使用框架的好处，所以一些细节莫钻牛角尖，学东西要明白重点。

2.2 损失函数

上面说到了，我们给出了一个函数模型\(f_{(w,b)}\)，其中\(w\)和\(b\)是函数\(f\)的位置变量，我们现在的目的就是通过已有的输入和输出求解出这两个变量。

为了得出这两个变量，我们这里引入一个专业术语损失（loss）函数，其实我很想写loss函数，因为有人也把它称作代价函数，但是相信有一定基础的人你一定明白，毕竟只是个名字而已，难道我叫吴彦祖我就是吴彦祖了？所以接下来所有的有多个名字的专业术语我都用我了解到的那个名字。

那么损失函数是什么意思呢？其实，顾名思义，就是一个损失，也就是一个差值，什么差值呢？就是我们假设未知变量\(w\)和\(b\)已知，简单点吧，我们假设\(w=b=0\)，然后我们根据这个未知变量就可以精准化我们的模型\(f\)，然后再通过这个模型以及输入和输出便可以得到一个预测值\(\hat{y}=w*x+b\)，由于我们的\(w\)和\(b\)是假设的，因此预测值\(\hat{y}\)和真实值\(y\)之间有一定的差值，这个差值就是损失，而对\(N\)个数据而言，总损失就是

\[loss = \sum_{i=1}^N{(\hat{y_i}-y_i)} \]

而损失函数指的是对损失的一种扩展，比如线性回归中最常使用的损失函数就是均方误差函数，如下：

\[loss = \frac{1}{N}\sum_{i=1}^N{(\hat{y_i}-y_i)}^2 \]

2.3 梯度下降

上面我们得到了一个均方误差的损失函数，然而可想而知，这个误差应该是越小越好，因此我们的目标就是最小化这个误差。上述这个损失函数，其实是一种凸函数，在凸优化理论中，可以使用梯度下降的方法来最小化这个凸函数，而当这个凸函数处于最小值时，此时的\(w\)和\(b\)也就是最优值，也就让\(\hat{y}\)和\(y\)的值更接近。

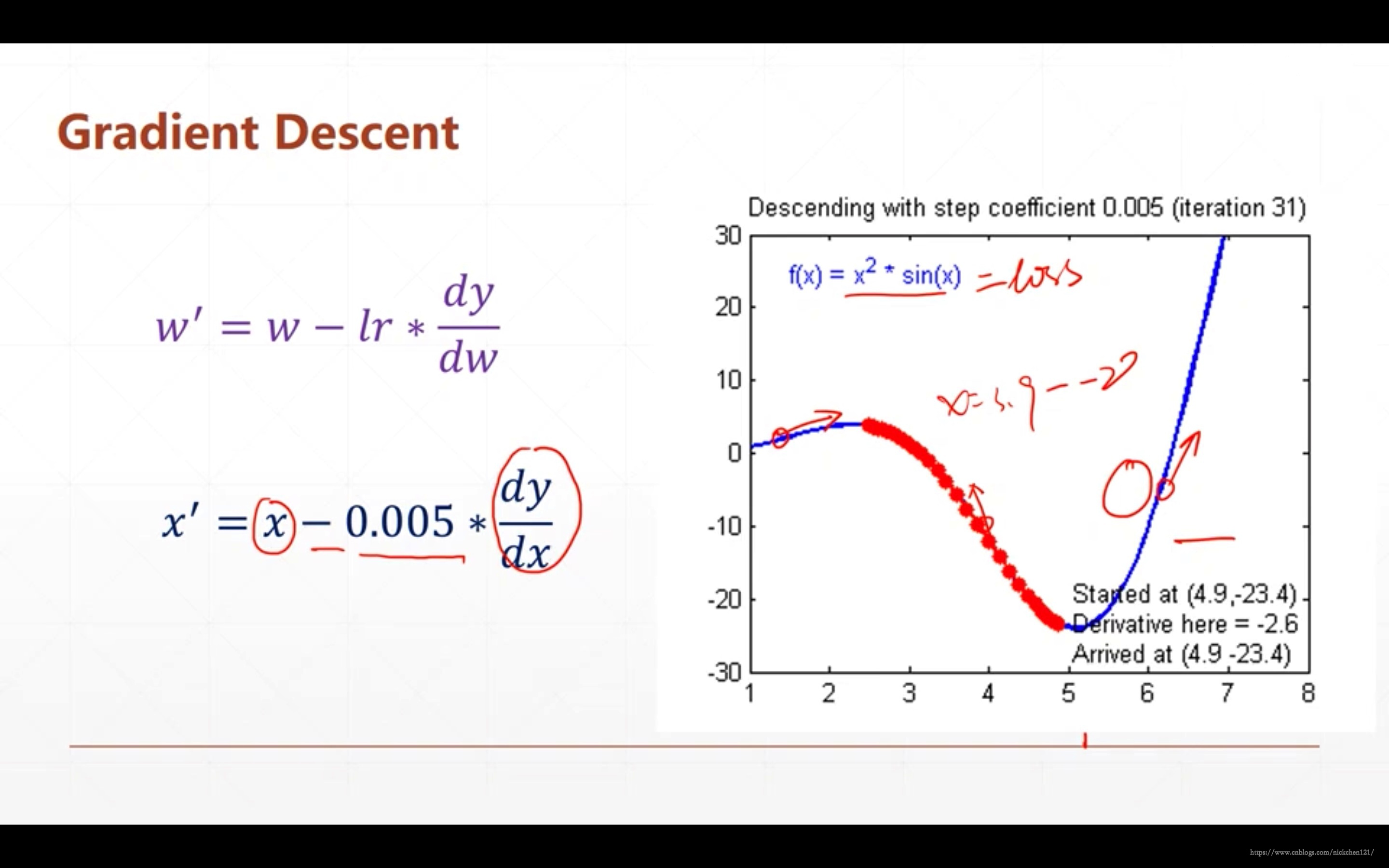
上述所示的函数就是一种凸函数，而该函数的最小值也显而易见。但是我们不能通过眼睛判断该函数的最小值，而可以通过梯度下降算法。这个算法的流程也很简单，就是按照某一点在x轴上的梯度的反方向一直前进即可。针对我们上述的\(w\)和\(b\)变量，则是：

\[w' = w - lr*\frac{\partial{loss}}{\partial{w}} \\ b' = b - lr*\frac{\partial{loss}}{\partial{b}} \]

从上式我们可以看到有一个\(lr\)，其实很好理解，梯度的求解可能是一个很大的值。如上图，如果在\(x=3\)时梯度值为30，那么\(x\)按照梯度的反方向前进就变成了\(33\)，很明显直接远离了最小值，因此可以通过控制\(lr\)的大小控制当\(x\)在某一点的移动范围，\(lr\)大一点则前进的快，\(lr\)小一点则前进的慢。

三、解决线性回归问题的五个步骤

从上面一节我们可以看出线性回归的流程简单点可以分为5个步骤：

1. 初始化未知变量\(w=b=0\)
2. 得到损失函数\(loss = \frac{1}{N}\sum_{i=1}^N{(\hat{y_i}-y_i)}^2\)
3. 利用梯度下降算法更新得到\(w', b'\)
4. 重复步骤3，利用\(w', b'\)得到新的更优的\(w', b'\)，直至\(w', b'\)收敛
5. 最后得到函数模型\(f=w'*x+b'\)

四、利用Numpy实战解决线性回归问题

步骤1代码：略

步骤2代码：计算训练数据的均方误差

def compute_error_for_line_given_points(b, w, points):
    """
    y = wx + b, 计算训练数据的均方误差
    :param b: 参数b，初始为0
    :param w: 参数w，初始为0
    :param points: 训练数据，100个二元组，如[(1,2),...,(100,200)]
    :return: 均方误差
    """

    total_error = 0  # 定义误差初始值

    # 计算训练数据的总误差
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        # 计算总误差
        total_error += ((y - w * x + b)) ** 2

    return total_error / float(len(points))  # 返回均方误差

步骤3代码：计算梯度并更新w和b

def step_gradient(b_current, w_current, points, learning_rate):
    """
    计算梯度并更新w和b
    :param b_current: 更新前的b
    :param w_current: 更新前的w
    :param points: 训练数据，100个二元组，如[(1,2),...,(100,200)]
    :param learning_rate: 学习速率
    :return: 更新后的w和b
    """

    b_gradient = 0
    w_gradient = 0
    N = float(len(points))

    # 更新梯度
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        # grad_b = 2(w * x + b - y)，b的求偏导结果
        b_gradient += (2 / N) * ((w_current * x + b_current) - y)  # update b
        # grad_w = 2(w * x + b - y) * x，w的求偏导结果
        w_gradient += (2 / N) * x * ((w_current * x + b_current) - y)  # update w

    # 更新后的w和b
    new_b = b_current - (learning_rate * b_gradient)
    new_w = w_current - (learning_rate * w_gradient)

    return [new_b, new_w]  # 返回更新后的w和b

步骤4代码：循环训练并更新w和b（此处我们循环训练1000次，而不是让参数收敛）

def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iterations):
    """
    循环训练并更新w和b
    :param points: 数据
    :param starting_b: b的初始值
    :param starting_w: w的初始值
    :param learning_rate: 学习速率
    :param num_iterations: 训练次数
    :return: 返回训练好的w和b
    """

    b = starting_b
    w = starting_w

    # 循环更新w和b
    for i in range(num_iterations):
        b, w = step_gradient(b, w, points, learning_rate)

    return [b, w]  # 返回训练好的b和w

    # 循环更新w和b
    for i in range(num_iterations):
        b,w = step_gradient(b,w,points,learning_rate)

    return [b,w] # 返回训练好的b和w

步骤5代码：最后得到函数模型\(f=w'*x+b'\)

五、总结

本篇文章讲解了机器学习中较为简单的线性回归算法，虽然很多细节没有涉及到，例如噪声的处理和正则化问题、方差和偏差问题、多元特征回归……

但是本篇文章的核心目的还是想让大家能够利用numpy实现线性回归模型，从最后的代码中可以看出，利用numpy我们就是在把前面的各种数学语言一个一个实现，求误差、求偏导、求梯度，这还只是最简单的回归问题，如果更复杂呢？我们也这样，怕是能让你秃头。

也因此，我们不得不引出我们接下来要讲的框架，他有什么好处，他的好处就是把我们上面的是三个函数封装好了，你需要做的仅仅只是调个函数，传个参数即可。