第10章 内排序

第10章 内排序

目录

• 第10章 内排序
• 一、排序的基本概念
  • 1.1 排序算法的记录存储结构定义
• 二、插入排序
  • 2.1 直接插入排序
  • 2.1.1 直接插入排序算法（算法）
  • 2.2 二分法（折半）插入排序
  • 2.3 表插入排序（大纲未规定）
  • 2.4 希尔（Shell）插入排序
• 三、选择排序
  • 3.1 直接选择排序
    • 3.1.1 直接选择排序算法（算法）
  • 3.2 树型选择排序（大纲未规定）
  • 3.3 堆排序
• 四、交换排序
  • 4.1 冒泡排序
  • 4.2 快速排序
• 五、归并排序
• 六、基数排序
  • 6.1 多排序码的排序
  • 6.2 静态链式基数排序
• 七、各种内部排序算法的比较（书中未给出）
• 八、内部排序算法的应用（书中未给出）
• 九、算法设计题
• 十、错题集

数据结构与算法_师大完整教程目录（更有python、go、pytorch、tensorflow、爬虫、人工智能教学等着你）：https://www.cnblogs.com/nickchen121/p/13768298.html

一、排序的基本概念

1. 排序：假设一个文件由 \(n\) 个记录 \(R_1,R_2,\cdots,R_n\) 组成，以记录中某个（或几个）字段值不减（或不增）的次序把这 \(n\) 个记录重新排列，称该字段为排序码
2. 关键码：能唯一标识一个记录的字段，关键码可以作为排序码，但排序码不一定要是关键码
3. 稳定排序算法：任意两个排序码相同的记录 \(R_i\) 和 \(R_j\)，如果排序前 \(R_i\) 在 \(R_j\) 的前面，排序后 \(R_i\) 还在在 \(R_j\) 的前面，则该算法是稳定的排序算法，否则是不稳定的排序算法
4. 注：以下讨论的排序，都是以记录中某个字段值不减的次序把这 \(n\) 个记录重新排列，且排序码数据类型为整型

1.1 排序算法的记录存储结构定义

#define MAXSIZE 100 // 文件中记录个数的最大值
typedef int keytype; // 定义排序码类型为整数类型
typedef struct {
    keytype key;
    // int other; // 此处还可以定义记录中除排序码外的其它域
} recordtype; // 记录类型的定义
typedef struct {
    recordtype r[MAXSIZE + 1];
    int length; // 待排序文件中记录的个数
} table; // 待排序文件类型

二、插入排序

2.1 直接插入排序

1. 算法步骤：

   1. 初始认为文件中的第 \(1\) 个记录已排好序
   2. 然后把第 \(2\) 个到第 \(n\) 个记录依次插入到已排序的记录组成的文件中
   3. 对第 \(i\) 个记录 \(R_i\) 进行插入时，\(R_1,R_2,\cdots,R_{i-1}\) 已排序

把记录 \(R_i\) 的排序码 \(key_i\) 和已经排好序的排序码从右向左依次比较，找到 \(R_i\) 应插入的位置
把该位置以后直到 \(R_{i-1}\) 的记录顺序后移，空出位置让 \(R_i\) 插入
6. 注：当待插入排序小于所有已排序的排序码时，可能会出现下标越界，因此可以在排序文件的第一个排序码前插入一个值作为哨兵
2. 图10-2-直接插入排序算法的执行过程示意图：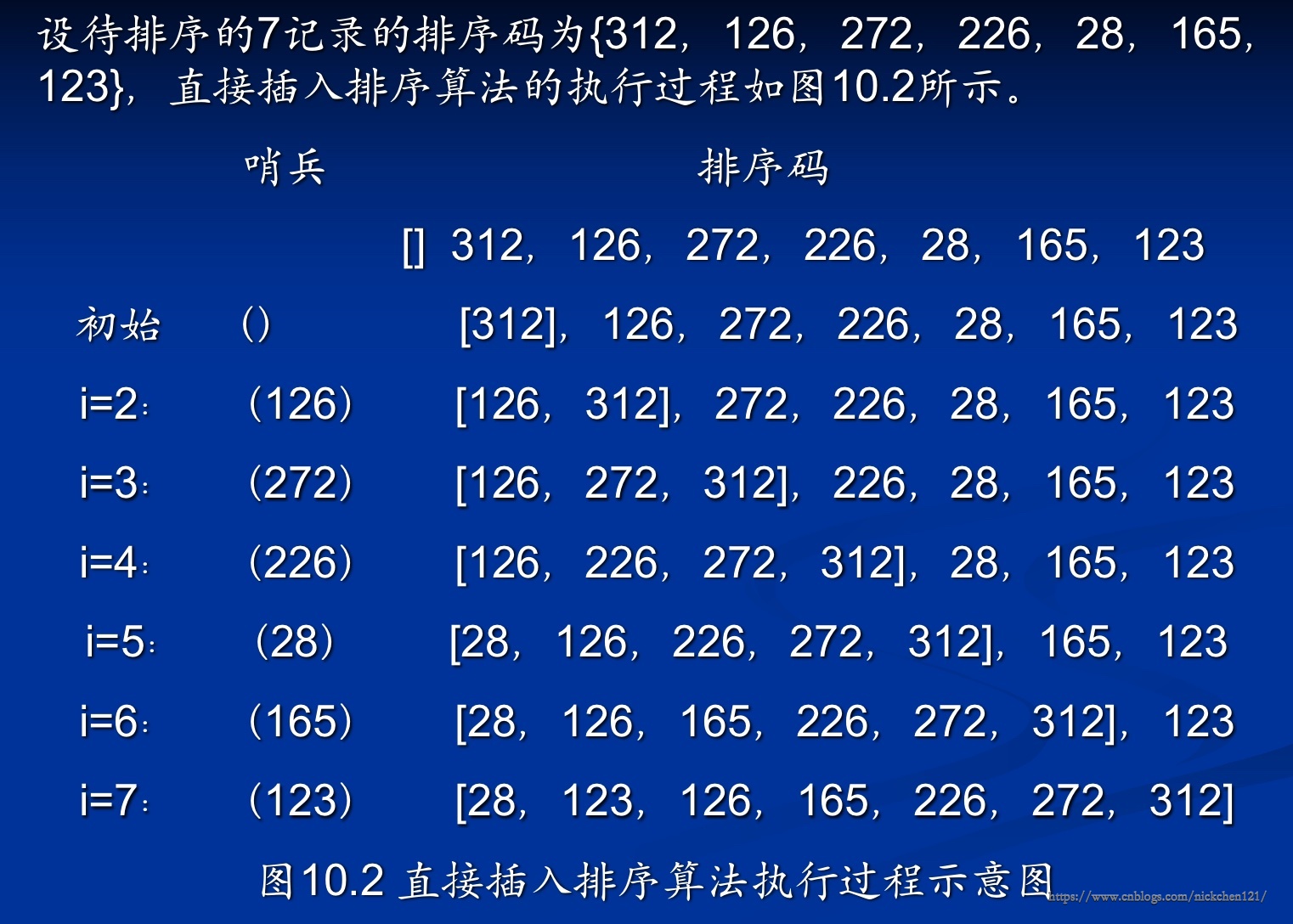

2.1.1 直接插入排序算法（算法）

void insertsort(table *tab) {
    int i, j;
    // 依次插入从第2个开始的所有元素
    for (i = 2; i <= tab->length; i++) {
        j = i - 1;
        tab->r[0].key = tab->r[i].key; // 设置哨兵，准备找插入位置

        // 找插入位置并后移
        while (tab->r[0].key < tab->r[j].key) {
            tab->r[j + 1].key = tab->r[j].key; // 后移
            j = j - 1; // 继续向前（左）查找
        }
        tab->r[j + 1].key = tab->r[0].key; // 插入第i个元素的副本，即前面设置的哨兵
    }
}

时间复杂度：\(O(n^2)\)

2.2 二分法（折半）插入排序

1. 算法步骤：

   1. 注：依据直接插入排序的思想，进行扩充
   2. 在找第 \(i\) 个记录的插入位置时，由于前 \(i-1\) 个记录已排好序，因此在插入过程中使用二分法确定 \(key[i]\) 的插入位置

2. 算法代码：略

2.3 表插入排序（大纲未规定）

1. 略

2.4 希尔（Shell）插入排序

1. 算法步骤：

   1. 对 \(n\) 个记录进行排序，首先取一个整数 \(d<n\)，把这个 \(n\) 个记录分成 \(d\) 组
   2. 所有位置相差为 \(d\) 的倍数的记录分在同一组
   3. 在每组中使用直接插入排序进行组内排序
   4. 缩小 \(d\) 的值
   5. 重复进行分组和组内排序
   6. 知道 \(d=1\) 结束排序

2. 算法代码：略

3. 图10-5-Shell插入排序示意图：

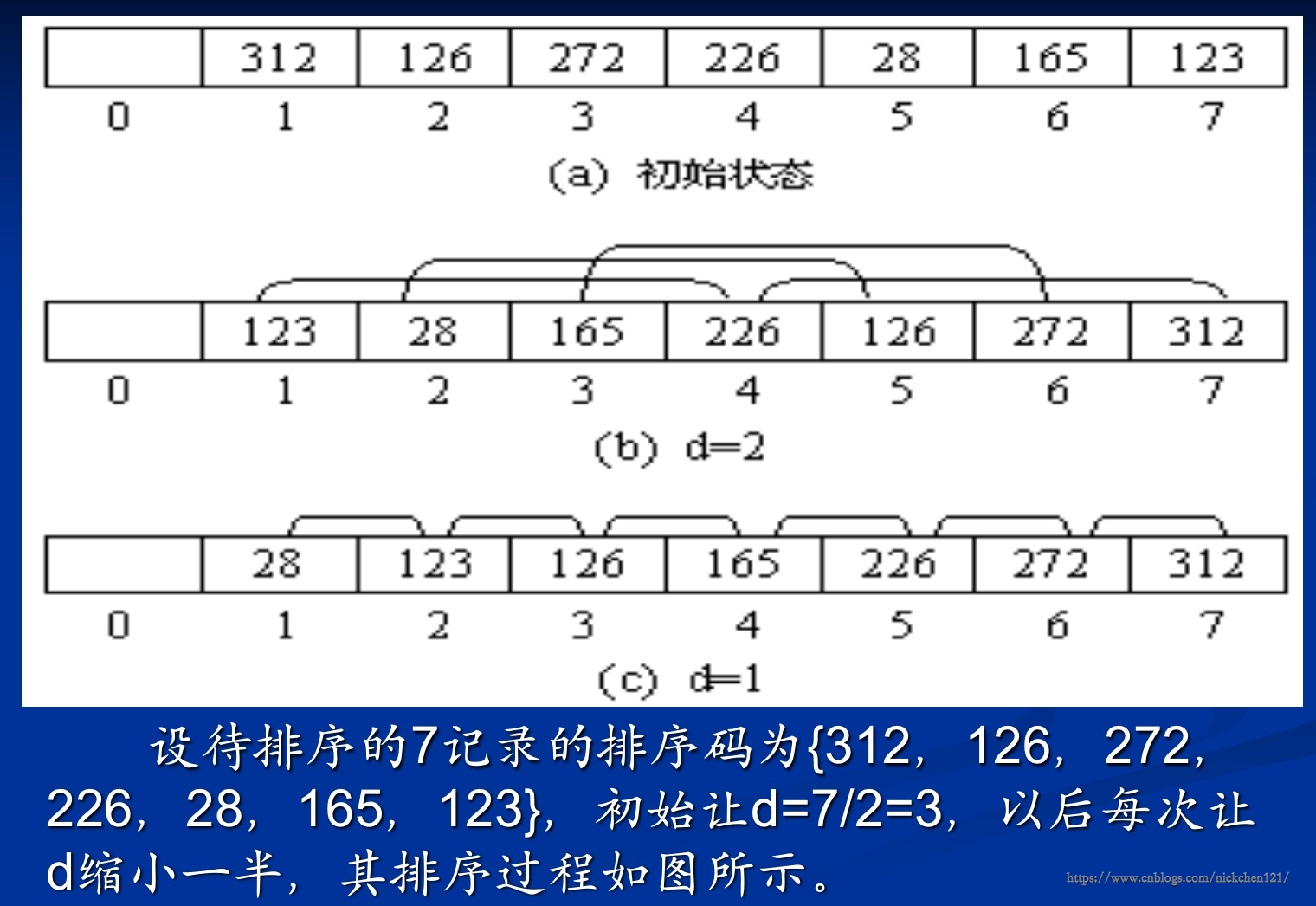
三、选择排序

1. 选择排序基本思想：每次从待排序文件中选择出排序码最小的记录，把该记录放入已排序文件的最后一个位置

3.1 直接选择排序

1. 算法步骤：

   1. 首先从 \(n\) 个记录中选择排序码最小的记录，让该记录和第 \(1\) 个记录交换
   2. 再从剩下的 \(n-1\) 个记录选出排序码最小的记录，让该记录和第 \(2\) 个记录交换
   3. 重复这样的操作直到剩下最后两个记录
   4. 从最后两个记录中选出最小的记录和第 \(n-1\) 个记录交换
   5. 结束

2. 图10-6-直接选择排序算法执行过程：

3.1.1 直接选择排序算法（算法）

void simpleselectsort(table *tab) {
    int i, j, k;
    for (i = 1; i <= tab->length - 1; i++) {
        k = i; // 记下当前最小元素的位置

        // 向右查找更小的元素
        for (j = i + 1; j <= tab->length; j++)
            if (tab->r[j].key < tab->r[k].key) k = j; // 修改当前最小元素的位置
            
        // 如果第i次选到的最小元素位置k不等于i，则将第k、i个元素交换
        if (k != i) {
            tab->r[0].key = tab->r[k].key;  // 以第0个元素作为中间单元进行交换
            tab->r[k].key = tab->r[i].key;
            tab->r[i].key = tab->r[0].key;
        }
    }
}

时间复杂度：\(O(n^2)\)

3.2 树型选择排序（大纲未规定）

3.3 堆排序

1. 堆排序解决的问题：保存中间比较结果，减少后面的比较次数，又不占用大量的附加存储空间

2. 堆：一个序列 \(\{k_1,k_2,\cdots,k_n\}\)，其中 \(k_i\leq{k_{2i}}\) 且 \(k_i\leq{k_{2i+1}}\)，当 \(i=1,2,\cdots,n/2\) 且 \(2i+1\leq{n}\)

   1. 注：当采用顺序存储这个序列，就可以把这个序列的每一个元素 \(k_i\) 看成是一颗有 \(n\) 个结点的完全二叉树的第 \(i\) 个结点，其中 \(k_1\) 是该二叉树的根结点

3. 堆的特征：把堆对应的一维数组看作一颗完全二叉树的顺序存储，则该完全二叉树中任意分支结点的值都小于或等于它的左右儿子结点的值，且根结点的值是所有元素中值最小的

4. 最小堆和最大堆：当父节点的值总是大于等于任何一个子节点的值时为最大堆； 当父节点的值总是小于等于任何一个子节点的值时为最小堆

5. 堆排序使用条件：当对记录 \(n\) 较大的文件，堆排序很好，当 \(n\) 较小时，并不提倡使用，因为初始建堆和调整建新堆时需要进行反复的筛选

6. 图10-8-一个序列 Arr = {5, 1, 13, 3, 16, 7, 10, 14, 6, 9}和相应的完全二叉树：

7. 构造最大堆步骤（通过已有完全二叉树构建堆）：

   1. 主要思想：判断有子女结点的子树是否满足最大（小）堆的要求
   2. 首先我们需要找到最后一个结点的父结点如图 \((a)\)，我们找到的结点是 \(16\)，然后找出该结点的最大子节点与自己比较，若该子节点比自身大，则将两个结点交换。图 \((a)\) 中，\(16\) 是最大的结点，不需要交换
   3. 我们移动到第下一个父结点 \(3\)，如图 \((b)\) 所示。同理做第一步的操作，交换了 \(3\) 和 \(14\)，结果如图 \((c)\) 所示
   4. 移动结点到下一个父结点 \(13\)，如图 \((d)\) 所示，发现不需要做任何操作
   5. 移动到下个父结点 \(1\)，如图 \((e)\) 所示,然后交换 \(1\) 和 \(16\)，如图 \((f)\) 所示，此时我们发现交换后，\(1\) 的子节点并不是最大的，我们接着在交换，如图 \((g)\)所示
   6. 移动到父结点到 \(5\)，一次重复上述步骤，交换 \(5\) 和 \(16\)，在交换 \(14\) 和 \(5\)，在交换 \(5\) 和 \(6\) 所有节点交换完毕，最大堆构建完成

8. 图10-9-建堆过程示意图：

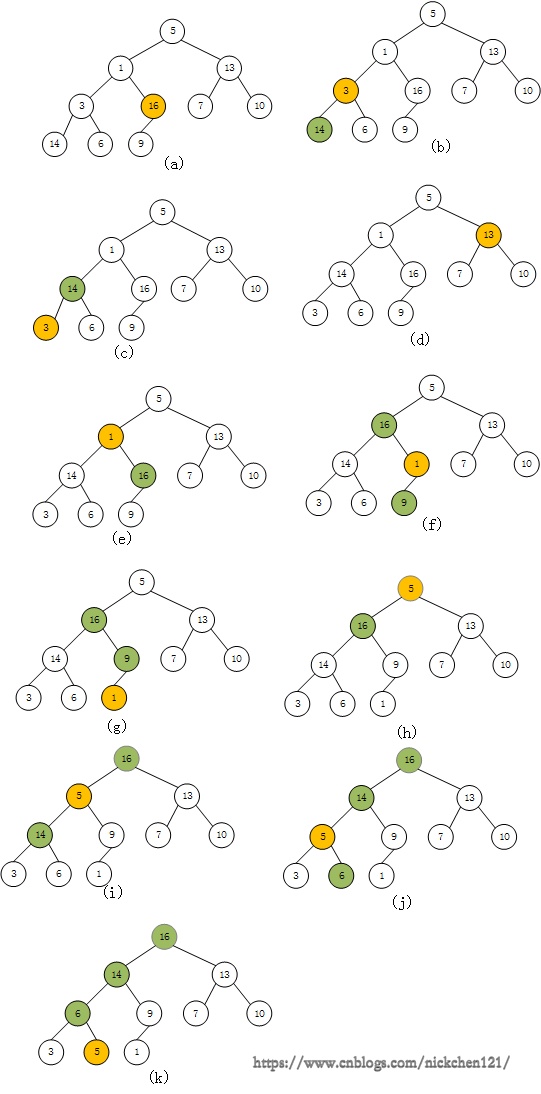
9. 堆排序步骤：

   1. 构建一个筛选算法，该算法可以把一个任意的排序码序列建成一个堆，堆的第一个元素就是排序码中最小的
   2. 把选出的最小排序码从堆中删除，对剩余的部分重新建堆，继续选出其中的最小者
   3. 直到剩余 \(1\) 个元素时，排序结束

四、交换排序

1. 交换排序：对待排序记录两两进行排序码比较，若不满足排序顺序，则交换这对排序码

4.1 冒泡排序

1. 冒泡排序算法步骤：

   1. 对所有记录从左到右每相邻两个记录的排序码进行比较，如果这两个记录的排序码不符合排序要求，则进行交换，这样一趟做完，将排序码最大者放在最后一个位置
   2. 对剩下的 \(n-1\) 个待排序记录重复上述过程，又将一个排序码放于最终位置，反复进行 \(n-1\) 次，可将 \(n-1\) 个排序码对应的记录放至最终位置，剩下的即为排序码最小的记录，它在第 \(1\) 的位置处
   3. 注：如果在某一趟中，没有发生交换，则说明此时所有记录已经按排序要求排列完毕，排序结束

2. 图10-10-冒泡排序算法示意图：

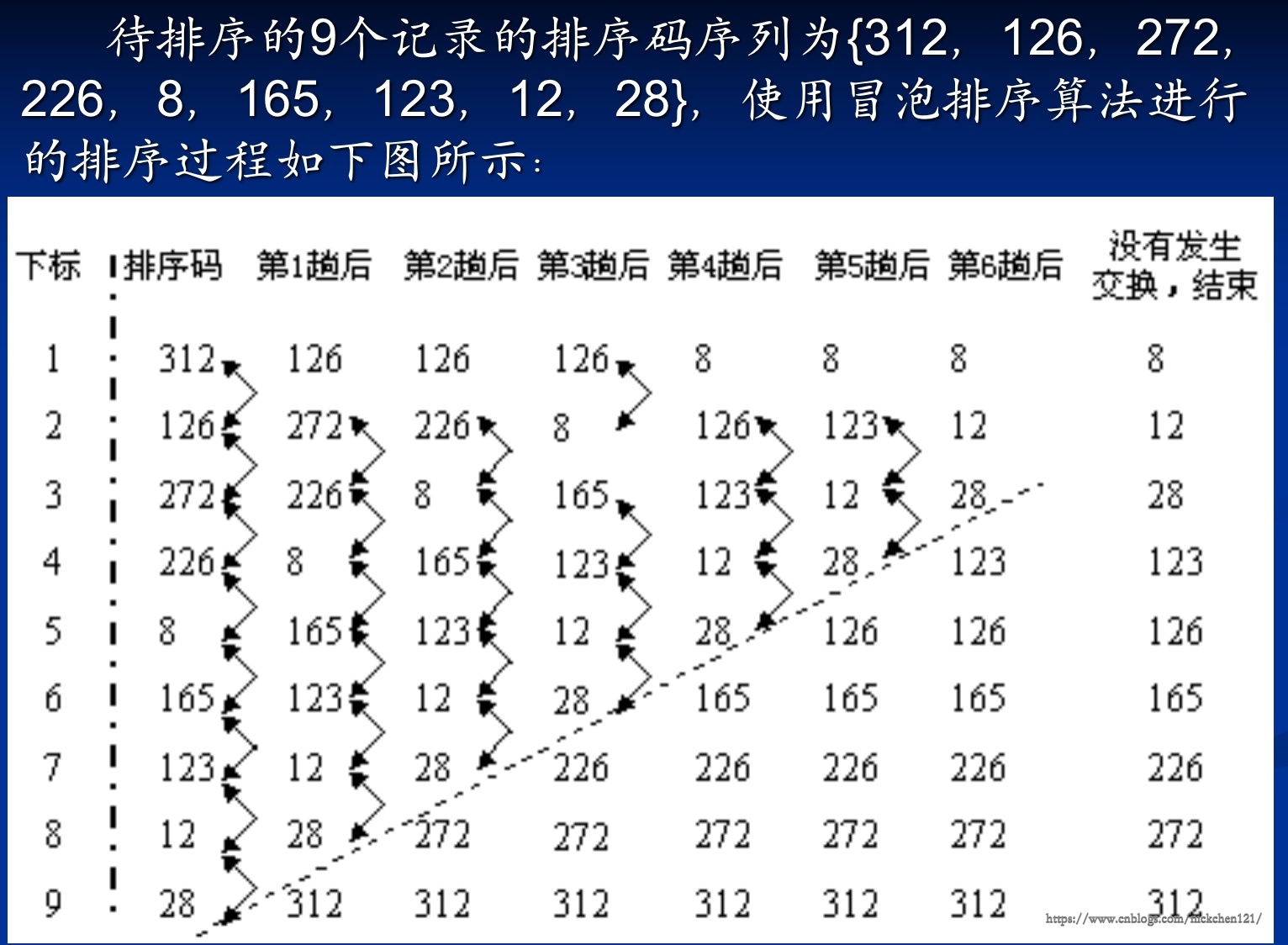
4.2 快速排序

1. 快速排序算法步骤（主要通过首尾指针的移动来划分大于 \(x\) 和小于 \(x\) 的值）：

   1. 从 \(n\) 个待排序的记录中任取一个记录(不妨取第 \(1\) 个记录)
   2. 设法将该记录放置于排序后它最终应该放的位置，使它前面的记录排序码都不大于它的排序码，而后面的记录排序码都大于它的排序码
   3. 然后对前、后两部分待排序记录重复上述过程，可以将所有记录放于排序成功后的相应位置，排序即告完成

2. 图10-11-一次划分的过程：

五、归并排序

1. 归并排序算法基本思路：一个待排序记录构成的文件，可以看作是有多个有序子文件组成的，对有序子文件通过若干次使用归并的方法，得到一个有序文件

2. 归并：把两个（或多个）有序子表合并成一个有序表的过程

3. 一次归并：把一个数组中两个相邻的有序数组归并为一个有序数组段，其结果存储于另一个数组

4. 一趟归并：\(n\) 个元素的数组中，从第 \(1\) 个元素开始，每连续 \(len\) 个元素组成的数组段是有序的，从第一个数组段开始，每相邻的两个长度相等的有序数组段进行一次归并，一直到剩余元素个数小于 \(2*len\)时结束。如果剩余元素个数大于 \(len\)，可以对一个长度为 \(len\)，另一个长度小于 \(len\) 的两个有序数组实行一次归并；如果其个数小于 \(len\)，则把这些元素直接拷贝到目标数组中

5. 图10-13-一趟归并的图示：

6. 二路归并排序算法步骤：

   1. 对任意一个待排序的文件，初始时它的有序段的长度为 \(1\)
   2. 通过不断调用一趟归并算法，使有序段的长度不断增加
   3. 直到有序段的长度不小于待排序文件的长度，排序结束

7. 图10-14-二路归并排序过程示意图：

六、基数排序

1. 基数排序（又称分配排序）：不对排序码比较，而是借助于多排序码排序的思想进行单排序吗排序的方法

6.1 多排序码的排序

1. 注： 每一张牌有两个 “排序码”：花色（梅花<方块<红心<黑桃）和面值（\(2<3<\ldots<A\)），且花色的地位高于面值，即面值相等的两张牌，以花色大的为大，即在比较两张牌的牌面大小时，先比较花色，若花色相同，则再比较面值
2. 分配：把 \(52\) 张扑克牌按面值分成 \(13\) 堆，再按照不同的花色分成 \(4\) 堆，分成若干堆的过程称为分配
3. 收集：第一次分配时，把面值不同的 \(13\) 堆牌自小至大叠在一起，把不同花色的 \(4\) 堆牌自小至大的次序合在一起，从若干堆自小到大叠在一起的过程称为收集

6.2 静态链式基数排序

1. 静态链式基数排序步骤：

   1. 先用静态链表存储待排序文件中的 \(n\) 个记录，表中每一个结点对应一个记录
   2. 第一趟对低位排序码（个位数）进行分配，将 \(n\) 个结点分配到序号分别为 \(0-9\) 的 \(10\) 个链式队列中，用 \(f[i]\) 和 \(e[i]\) 分别作为第 \(i\) 个队列的队首和队尾指针
   3. 第一趟收集过程中把这个 \(10\) 个队列中非空的队列依次合并在一起产生一个新的静态单链表
   4. 对这个新的静态单链表按十位数进行分配和采集，然后再依次对百位数、千位数直到最高位数反复进行这样的分配和收集操作，排序结束

2. 图10-15-静态链式技术排序示意图：

七、各种内部排序算法的比较（书中未给出）

排序方法	比较次数（最好）	比较次数（最差）	移动次数（最好）	移动次数（最差）	稳定性
直接插入排序	\(n\)	\(n^2\)	\(0\)	$$n^2$$	\(√\)
折半插入排序	\(nlog_2n\)	\(nlog_2n\)	\(0\)	\(n^2\)	\(√\)
冒泡排序	\(n\)	\(n^2\)	\(0\)	\(n^2\)	\(√\)
快速排序	\(nlog_2n\)	\(n^2\)	\(nlog_2n\)	\(n^2\)	\(×\)
简单选择排序	\(n^2\)	\(n^2\)	\(0\)	\(n\)	\(×\)
堆排序	\(nlog_2n\)	\(nlog_2n\)	$$nlog_2n$$	\(nlog_2n\)	\(×\)
归并排序	\(nlog_2n\)	\(nlog_2n\)	\(nlog_2n\)	\(nlog_2n\)	\(√\)
基数排序	\(O(b(n+rd))\)	\(O(b(n+rd))\)			\(√\)

上表基数排序中：\(rd\) 是收集过程和各位排序码的取值范围中值的个数（十进制为 \(10\)）；静态链式基数排序要进行 \(b\) 唐收集和分配

八、内部排序算法的应用（书中未给出）

1. 略

九、算法设计题

1. 略

十、错题集

1. 下列说法错误的是：基数排序适合实型数据的排序
2. 插入排序算法在最后一趟开始之前，所有的元素可能都不在其最终的位置上（比如最后一个需要插入的元素是最小的元素）
3. 一个序列中有 \(10000\) 个元素，若只想得到其中前 \(10\) 个最小元素，最好采用堆排序算法
4. 排序的趟数和待排序元素的原始状态有关的排序算法是冒泡排序
5. 快速排序算法和冒泡排序算法都会出现起泡的现象