02-31 线性支持向量机

目录

人工智能从入门到放弃完整教程目录：https://www.cnblogs.com/nickchen121/p/11686958.html

线性支持向量机

在线性可分支持向量机中说到线性可分支持向量机有一个缺点是无法对异常点做处理，也正是因为这些异常点导致数据变得线性不可分或者会因为它的正好被判断为支持向量导致模型的泛化能力变差。

# 异常点导致数据线性不可分图例
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')

x1 = [2, 2.5, 3.2, 6.5]
x11 = [1, 4.5, 5, 6]
x2 = [1.2, 1.4, 1.5, 1.2]
x22 = [1, 1.5, 1.3, 1]

plt.scatter(x1, x2, s=50, color='b')
plt.scatter(x11, x22, s=50, color='r')
plt.vlines(3.9, 0.8, 2, colors="g", linestyles="-",
           label='$w*x+b=0$', alpha=0.2)
plt.text(1.1, 1.1, s='异常点A', fontsize=15, color='k',
         ha='center', fontproperties=font)
plt.text(6.3, 1.3, s='异常点B', fontsize=15, color='k',
         ha='center', fontproperties=font)
plt.legend()
plt.show()

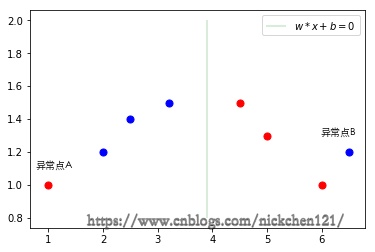
上图可以看出由于异常点A和异常点B可能导致无法按照线性可分支持向量机对上述数据集分类。

# 异常点导致模型泛化能力变差图例
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
from sklearn import svm
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')

np.random.seed(8)  # 保证数据随机的唯一性

# 构造线性可分数据点
array = np.random.randn(20, 2)
X = np.r_[array-[3, 3], array+[3, 3]]
y = [0]*20+[1]*20

# 建立svm模型
clf = svm.SVC(kernel='linear')
clf.fit(X, y)

# 构造等网个方阵
x1_min, x1_max = X[:, 0].min(), X[:, 0].max(),
x2_min, x2_max = X[:, 1].min(), X[:, 1].max(),
x1, x2 = np.meshgrid(np.linspace(x1_min, x1_max),
                     np.linspace(x2_min, x2_max))

# 得到向量w: w_0x_1+w_1x_2+b=0
w = clf.coef_[0]
# 加1后才可绘制 -1 的等高线 [-1,0,1] + 1 = [0,1,2]
f = w[0]*x1 + w[1]*x2 + clf.intercept_[0] + 1

# 绘制H2，即wx+b=-1
plt.contour(x1, x2, f, [0], colors='k', linestyles='--', alpha=0.1)
plt.text(2, -4, s='$H_2={\omega}x+b=-1$', fontsize=10, color='r', ha='center')

# 绘制分隔超平面，即wx+b=0
plt.contour(x1, x2, f, [1], colors='k', alpha=0.1)
plt.text(2.5, -2, s='$\omega{x}+b=0$', fontsize=10, color='r', ha='center')
plt.text(2.5, -2.5, s='分离超平面', fontsize=10,
         color='r', ha='center', fontproperties=font)

# 绘制H1，即wx+b=1
plt.contour(x1, x2, f, [2], colors='k', linestyles='--')
plt.text(3, 0, s='$H_1=\omega{x}+b=1$', fontsize=10, color='r', ha='center')

# 绘制数据散点图
plt.scatter(X[0:20, 0], X[0:20, 1], cmap=plt.cm.Paired, marker='x')
plt.text(1, 1.8, s='支持向量', fontsize=10, color='gray',
         ha='center', fontproperties=font)

plt.scatter(X[20:40, 0], X[20:40, 1], cmap=plt.cm.Paired, marker='o')
plt.text(-1.5, -0.5, s='支持向量', fontsize=10,
         color='gray', ha='center', fontproperties=font)

# 绘制假设的异常点及假设的间隔边界，**毫无意义的代码**，为了讲解用
plt.scatter(-1.5, 3, marker='x', c='b')
plt.text(-1.5, 3.1, s='异常点A', fontsize=10,
         color='r', ha='center', fontproperties=font)
x_test = np.linspace(-3, 4, 666)
y_test = -(w[0]+0.12)*x_test - (w[1]-0.002)*x_test+clf.intercept_[0]+1.8
y_test_test = -(w[0]+0.12)*x_test - (w[1]-0.002)*x_test+clf.intercept_[0]+2.3

plt.plot(x_test, y_test, linestyle='--')
plt.plot(x_test, y_test_test)

plt.xlim(x1_min-1, x1_max+1)
plt.ylim(x2_min-1, x2_max+1)
plt.show()

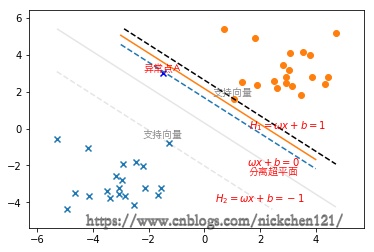
上图可以看出由于异常点导致分离超平面从淡实线变成了黄色的那条曲线，从图中可以明显看出异常点严重影响了模型的泛化能力。

这次讲到的线性支持向量机（linear support vector machine）将修改线性可分支持向量机的硬间隔最大化为软间隔最大化解决上面有异常点导致的问题。

一、线性支持向量机学习目标

  1. 硬间隔最大化和软间隔最大化的区别
  2. 线性支持向量机的支持向量
  3. 合页损失函数
  4. 线性支持向量机的步骤

二、线性支持向量机详解

2.1 硬件隔最大化和软间隔最大化

2.1.1 硬间隔最大化

线性可分支持向量机中说到线性可分支持向量机的目标函数的最优化问题属于硬间隔最大化，即

\[\begin{align} & \underbrace{\min}_{\omega,b} {\frac{1}{2}}{||\omega||}^2 \\ & s.t. \quad y_i(\omega{x_i}+b)\geq1, \quad i=1,2,\ldots,m \end{align} \]

2.1.2 软间隔最大化

上一节讲到异常点会导致数据线性不可分，即意味着某些样本点不能满足函数间隔大于等于\(1\)的约束条件，为了解决该问题可以对每个样本点\((x_i,y_i)\)引进一个松弛变量\(\xi_i\geq0\)，使得函数间隔加上松弛变量大于等于1，因此约束条件将变成

\[y_i(wx_i+b)\geq1-\xi_i \]

相比较硬间隔最大化，可以看到样本到分离超平面的函数距离要求放松了，之前一定要大于等于\(1\)，现在只需要加上一个大于等于\(0\)的松弛变量大于等于\(1\)即可。同时，每个松弛变量\(\xi_i\)对应一个代价\(\xi_i\)，则目标函数变成了

\[{\frac{1}{2}}{||\omega||}^2 + C\sum_{i=1}^m\xi_i \]

其中\(C>0\)称为惩罚参数，\(C\)值越大，对误分类样本惩罚越大，即间隔宽度越小；\(C\)值越小，对误分类样本惩罚越小，即间隔宽度越大。

现在的目标函数有两层意思，即希望\({\frac{1}{2}}{||\omega||}^2\)尽量小的同时误分类样本也尽可能的少，\(C\)则是协调两者关系的正则化惩罚系数。上面的思路较于硬间隔最大化称为软间隔最大化，也因此线性支持向量机的原始问题为

\[\begin{align} & \underbrace{\min}_{\omega,b,\xi} {\frac{1}{2}}{||\omega||}^2 + C\sum_{i=1}^m\xi_i \\ & s.t. \quad y_i(\omega{x_i}+b)\geq1-\xi_i, \quad i=1,2,\ldots,m \\ & \quad\quad \xi_i\geq0, \quad i=1,2,\ldots,m \end{align} \]

2.2 线性支持向量机定义

对于给定的线性不可分的训练数据集，通过求解上一节的线性支持向量的原始问题即凸二次规划问题即软间隔最大化问题，假设问题的解释\(w^*\)和\(b^*\)，得到的分离超平面为

\[w^*x+b^*=0 \]

分类决策函数为

\[f(x) = sign(w^*x+b*) \]

称作线性支持向量机。

2.3 软间隔最大化即目标函数的优化

线性支持向量机的原始问题为

\[\begin{align} & \underbrace{\min}_{\omega,b,\xi} {\frac{1}{2}}{||\omega||}^2 + C\sum_{i=1}^m\xi_i \\ & s.t. \quad y_i(\omega{x_i}+b)\geq1-\xi_i, \quad i=1,2,\ldots,m \\ & \quad\quad \xi_i\geq0, \quad i=1,2,\ldots,m \end{align} \]

通过线性支持向量机的原始问题可得原始问题的拉格朗日函数为

\[L(\omega,b,\xi,\alpha,\mu)={\frac{1}{2}}{||w||}^2+C\sum_{i=1}^m\xi_i-\sum_{i=1}^m\alpha_i(y_i(wx_i+b)-1+\xi_i)-\sum_{i=1}^m\mu_i\xi_i \]

其中\(\mu_i\geq0,\alpha_i\geq0\)，均为拉格朗日系数。

即现在需要优化的目标函数为

\[\underbrace{\min}_{\omega,b,\xi}\underbrace{\max}_{\mu_i\geq0,\alpha_i\geq0}L(\omega,b,\alpha,\xi,\mu) \]

由于优化的目标函数满足KKT条件，即可以通过拉格朗日对偶将上述的优化问题转化为等价的对偶问题为

\[\underbrace{\max}_{\mu_i\geq0,\alpha_i\geq0} \underbrace{\min}_{\omega,b,\xi} L(\omega,b,\alpha,\xi,\mu) \]

对偶问题为拉格朗日函数的极大极小问题，因此首先求\(L(\omega,b,\alpha,\xi,\mu)\)对\(\omega,b,\xi\)的极小，即

\[\begin{align} & \nabla_wL(\omega,b,\alpha,\xi,\mu)=w-\sum_{i=1}^m\alpha_iy_ix_i=0 \\ & \nabla_bL(\omega,b,\alpha,\xi,\mu) = -\sum_{i=1}^m\alpha_iy_i=0 \\ & \nabla_{\xi_i}L(\omega,b,\alpha,\xi,\mu)=C-\alpha_i-\mu_i=0 \end{align} \]

得

\[\begin{align} & w=\sum_{i=1}^m\alpha_iy_ix_i \\ & \sum_{i=1}^m\alpha_iy_i=0 \\ & C-\alpha_i-\mu_i=0 \end{align} \]

将上述三个式子代入拉格朗日函数即可得（注：推导过程类似于线性可分支持向量机的推导过程，不多赘述，直接给出结果）

\[\underbrace{\min}_{\omega,b,\xi} L(\omega,b,\alpha,\xi,\mu) = -{\frac{1}{2}}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_ix_j)+\sum_{i=1}^m\alpha_i \]

通过\(\underbrace{\min}_{\omega,b,\xi} L(\omega,b,\alpha,\xi,\mu)\)即可得\(\alpha\)的极大，即将上式代入对偶问题得

\[\begin{align} & \underbrace{\max}_{\alpha} {-{\frac{1}{2}}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_ix_j)+\sum_{i=1}^m\alpha_i} \\ & s.t. \quad \sum_{i=1}^m\alpha_iy_i=0 \\ & \quad\quad C-\alpha_i-\mu_i=0 \\ & \quad\quad \alpha_i\geq0, \quad i=1,2,\ldots,m \\ & \quad\quad \mu_i\geq0, \quad i=1,2,\ldots,m \end{align} \]

由于\(C-\alpha_i-\mu_i=0\)并且\(\mu_i\geq0\)，即\(0\leq\alpha_i\geq{C}\)，再对目标函数变号，即变成求极小值

\[\begin{align} & \underbrace{\min}_{\alpha} {{\frac{1}{2}}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_ix_j)-\sum_{i=1}^m\alpha_i} \\ & s.t. \quad \sum_{i=1}^m\alpha_iy_i=0 \\ & \quad\quad 0\leq\alpha_i\geq{C} \end{align} \]

上式便是线性支持向量机的软间隔最大化问题，与线性可分支持向量机的硬间隔最大化问题相比仅仅是多了一个约束条件\(0\leq\alpha_i\geq{C}\)，即也可以通过SMO算法求出上式极小化对应的\(\alpha\)，假设通过SMO算法得到了该\(\alpha\)值记作\(\alpha^*\)，即可根据\(\alpha^*\)求得原始最优化问题的解\(\omega^*\)和\(b^*\)。

由于接下来的推导过程与线性可分支持向量机一样，不再赘述，值得说一句的是。《线性可分支持向量机》一文曾说道有多少个支持向量机则可能求出多少个\(b^*\)，线性可分支持向量机中的\(b^*\)都是一样的，可以不用处理；而线性支持向量机由于松弛因子的影响对于不同的支持向量\(b^*\)是不同的，通常使用取均值的方法得到最终的\(b^*\)。

2.4 支持向量

2.4.1 硬间隔最大化支持向量

硬间隔最大化中的支持向量比较简单，即满足\(y_j(w^*x_j+b)-1=0\)即可。《线性可分支持向量机》曾给出解释：由KKT互补条件可得对于\(\alpha^*>0\)样本点\((x_j,y_j)\)有\(y_j(w^*x_j+b)-1=0\)，并且间隔边界\(H_1\)和\(H_2\)分别为\(w^*x_j+b^*=1\)和\(w^*x_j+b^*=-1\)，即支持向量一定在间隔边界上。

2.4.2 软间隔最大化支持向量

软间隔最大化的支持向量则由于对每个样本引入了松弛因子\((x_i,y_i)\)变得较为复杂。第\(i\)个样本\(x_i\)到对应类别支持向量的距离为\({\frac{\xi_i}{||w||}}\)，根据软间隔最大化时的KKT条件中的对偶互补条件\({\alpha_i}^*(y_i(wx_i+b)-1+\xi_i)=0\)可得

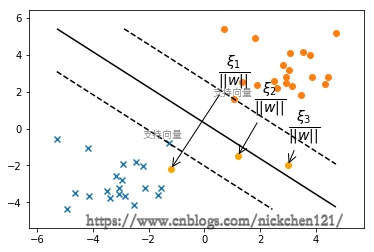
  1. 如果\({\alpha_i}^*=0\)，则\(\xi_i=0\),即样本在间隔边界上或者已经被正确分类，即下图中所有远离边界的点

  2. 如果\(0<{\alpha_i}^*<C\)，则\(\xi_i=0\),支持向量\(x_i\)恰好落在间隔边界上，即下图中的两个支持向量

  3. 如果\({\alpha_i}^*=C\)，说明这这可能是一个异常点，需要检查此时\(\xi_i\)的情况

    1. 如果\(0<{\xi_i}<1\)，则点\(x_i\)被正确分类，但是却在分离超平面和间隔边界之间，即下图中的点3
    2. 如果\(\xi_i=1\)，则点\(x_i\)在分离超平面上，即该点不能被正常分类
    3. 如果\(\xi_i>1\)，则点\(x_i\)位于分离超平面误分类一侧，即该点不能被正常分类，即下图中的点1和点2
# 软间隔最大化支持向量图例
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
from sklearn import svm
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')

np.random.seed(8)  # 保证数据随机的唯一性

# 构造线性可分数据点
array = np.random.randn(20, 2)
X = np.r_[array-[3, 3], array+[3, 3]]
y = [0]*20+[1]*20

# 建立svm模型
clf = svm.SVC(kernel='linear', C=10.0)
clf.fit(X, y)

# 构造等网个方阵
x1_min, x1_max = X[:, 0].min(), X[:, 0].max(),
x2_min, x2_max = X[:, 1].min(), X[:, 1].max(),
x1, x2 = np.meshgrid(np.linspace(x1_min, x1_max),
                     np.linspace(x2_min, x2_max))

# 得到向量w: w_0x_1+w_1x_2+b=0
w = clf.coef_[0]
# 加1后才可绘制 -1 的等高线 [-1,0,1] + 1 = [0,1,2]
f = w[0]*x1 + w[1]*x2 + clf.intercept_[0] + 1

# 绘制H2，即wx+b=-1
plt.contour(x1, x2, f, [0], colors='k', linestyles='--')

# 绘制分隔超平面，即wx+b=0
plt.contour(x1, x2, f, [1], colors='k')

# 绘制H1，即wx+b=1
plt.contour(x1, x2, f, [2], colors='k', linestyles='--')

# 绘制数据散点图
plt.scatter(X[0:20, 0], X[0:20, 1], cmap=plt.cm.Paired, marker='x')
plt.text(1, 1.8, s='支持向量', fontsize=10, color='gray',
         ha='center', fontproperties=font)

plt.scatter(X[20:40, 0], X[20:40, 1], cmap=plt.cm.Paired, marker='o')
plt.text(-1.5, -0.5, s='支持向量', fontsize=10,
         color='gray', ha='center', fontproperties=font)


# 绘制假设的异常点，**毫无意义的代码**，为了讲解用
plt.annotate(r'${\frac{\xi_1}{||w||}}$', xytext=(0.5, 2.8), xy=(-1.2, -2.2),
             arrowprops=dict(arrowstyle="->", connectionstyle="arc3"), fontsize=20)
plt.scatter(-1.2, -2.2, marker='o', c='orange')

plt.annotate(r'${\frac{\xi_2}{||w||}}$', xytext=(1.8, 1.3), xy=(
    1.2, -1.5), arrowprops=dict(arrowstyle="->", connectionstyle="arc3"), fontsize=20)
plt.scatter(1.2, -1.5, marker='o', c='orange')

plt.annotate(r'${\frac{\xi_3}{||w||}}$', xytext=(3, -0.2), xy=(
    3, -2), arrowprops=dict(arrowstyle="->", connectionstyle="arc3"), fontsize=20)
plt.scatter(3, -2, marker='o', c='orange')


plt.xlim(x1_min-1, x1_max+1)
plt.ylim(x2_min-1, x2_max+1)
plt.show()

2.5 合页损失函数

线性支持向量机还有另外一种解释，就是最小化以下目标函数

\[\sum_{i=1}^m [1-y_i(wx_i+b)]_{+}+\lambda{||w||}^2 \]

其中\(\sum_{i=1}^m [1-y_i(wx_i+b)]_{+}\)被称为经验损失，既可以度量模型的好坏；\(\lambda\)是正则化项。

其中函数\(L(y(wx+b))=[1-y_i(wx_i+b)]_{+}\)称为合页损失函数（hinge loss function），下标\(+\)表示为

\[{[z]}_+ = \begin{cases} z \quad z>0 \\ 0 \quad z\leq0 \end{cases} \]

也就是说，如果点被正确分类，即函数间隔\(y_i(wx_i+b)\)大于1，即\(z\leq0\)，损失是0；否则损失是\(1-y_i(wx_i+b)\)。但是对于上图的点3被正确分类但是损失不是0，因此合页损失函数对学习有更高的要求。

其实上述的目标函数等价于软间隔最大化的目标函数，即把\([1-y_i(wx_i+b)]_{+}\)看成\(\xi_i\)，即上述的目标函数可以写成

\[\underbrace{\min}_{\omega,b} \quad \sum_{i=1}^m\xi_i+\lambda{||\omega||}^2 \]

如果取\(\lambda\)为\({\frac{1}{2C}}\)，则

\[\underbrace{\min}_{\omega,b} \quad {\frac{1}{C}}({\frac{1}{2}}{||\omega||}^2+C\sum_{i=1}^m\xi_i) \]

软间隔最大化的目标函数为

\[\underbrace{\min}_{\omega,b} \quad {\frac{1}{2}}{||\omega||}^2+C\sum_{i=1}^m\xi_i \]

三、线性支持向量机流程

3.1 输入

有\(m\)个样本的线性可分训练集\(T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_m,y_m)\}\)，其中\(x_i\)为\(n\)维特征向量，\(y_i\)为二元输出即值为\(1\)或者\(-1\)。

3.2 输出

分离超平面的参数\(w^*\)和\(b^*\)以及分类决策函数

3.3 流程

  1. 构造约束优化问题为

\[\begin{align} & \underbrace{\min}_{\alpha} {\frac{1}{2}} \sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_ix_j) - \sum_{i=1}^m\alpha_i \\ & s.t. \sum_{i=1}^m \alpha_iy_i =0 \\ & \quad 0\geq\alpha_i\leq{C}, \quad i=1,2,\ldots,m \end{align} \]

  1. 使用SMO算法求出上式最小时对应的\(\alpha^*\)
  2. 计算\(w^*\)为

\[w^* = \sum_{i=1}^m \alpha^*y_ix_i \]

  1. 找到所有的\(S\)个支持向量，即满足\(0<{\alpha_i}^*<C\)的样本\((x_s,y_s)\)，通过\(y_s(\sum_{i=1}^S{\alpha_i}^*y_ix_ix_s+b^*)-1=0\)计算出每个支持向量对应的\(b^*\)，计算出这些所有的\(b^*\)的平均值即为最终的\(b^*={\frac{1}{S}}\sum_{i=1}^Sb^*\)。
  2. 求得分离超平面为

\[w^*x+b^* = 0 \]

  1. 求得分类决策函数为

\[f(x) = sign(w^*x+b^*) \]

线性支持向量机的步骤和线性可分支持向量机的步骤大致相同，由于线性支持向量机使用了松弛因子，两者之间最大的不同点在于对\(b^*\)值的考虑。

四、线性支持向量机优缺点

4.1 优点

  1. 处理了异常点导致的数据集线性不可分问题

4.2 缺点

  1. 只支持二分类问题，对于多分类问题需要使用OvR等其他辅助方法
  2. 只解决了异常点造成的非线性数据的处理，未真正解决非线性数据的分类问题

五、小结

线性支持向量机解决了最初的支持向量机的一个大问题，即无法处理原始问题，异常值会给模型的优化带来极大的麻烦，即会使得模型的最大间隔变窄，影响模型的性能。

虽然线性支持向量机支持这种异常值导致的数据集线性不可分，但是他并没有从本质上解决线性支持向量机无法处理线性不可分的问题，接下来的核函数的使用将让支持向量机变成分类器模型中的王者，即非线性支持向量机。

posted @ 2019-10-16 17:07  B站-水论文的程序猿  阅读(1863)  评论(0)  编辑  收藏  举报