05-01 特征预处理
人工智能从入门到放弃完整教程目录:https://www.cnblogs.com/nickchen121/p/11686958.html
特征预处理
之前说到构建机器学习系统的步骤中的第二步说到需要进行数据预处理,但是并没有说如何对数据进行预处理,这一章将会展开来说说将来建模时会碰到的各种脏数据的形式,以及对这种形式数据的处理方式,而对数据处理即对数据的特征进行处理。
一、特征预处理学习目标
- 缺失值处理
- 离群值处理
- 数据类型转换
- 归一化数据
- 二值化数据
二、特征预处理详解
2.1 缺失值处理
现实生活中的数据往往是不全面的,很多样本的属性值会有缺失,例如某个人填写的个人信息不完整或者对个人隐私的保护政策导致建模时可能无法得到所需要的特征,尤其是在数据量较大时,这种缺失值的产生会对模型的性能造成很大的影响。接下来将通过鸢尾花数据讨论缺失值处理的方法。
# 缺失值处理示例
import pandas as pd
from io import StringIO
iris_data = '''
5.1,,1.4,0.2,Iris-setosa
4.9,3.0,1.4,0.2,Iris-setosa
4.7,3.2,,0.2,Iris-setosa
7.0,3.2,4.7,1.4,Iris-versicolor
6.4,3.2,4.5,1.5,Iris-versicolor
6.9,3.1,4.9,,Iris-versicolor
,,,,Iris-setosa
'''
df = pd.read_csv(StringIO(iris_data), header=None)
# 强调:之后的代码只为方便中文阅读习惯的读者看起来方便,自己写代码特证属性名尽量不要用中文,不方便变量名的创建
df.columns = ['花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度', 'class_label']
df = df.iloc[:, :4]
df
| 花萼长度 | 花萼宽度 | 花瓣长度 | 花瓣宽度 | |
|---|---|---|---|---|
| 5.1 | NaN | 1.4 | 0.2 | |
| 4.9 | 3.0 | 1.4 | 0.2 | |
| 4.7 | 3.2 | NaN | 0.2 | |
| 7.0 | 3.2 | 4.7 | 1.4 | |
| 6.4 | 3.2 | 4.5 | 1.5 | |
| 6.9 | 3.1 | 4.9 | NaN | |
| NaN | NaN | NaN | NaN |
通过给定的鸢尾花数据,使用StringIO把字符串缓存成为文本,之后把该数据读入pandas。从pandas打印的结果可以明显的看到给出的数据中有3个NAN即缺失值。由于数据少,很容易看出有几个缺失值并且可以手动改变,但是工业上数据量是非常庞大的,这个时候可以调用pandas的isnull()。isnull()方法把数据集中存在的值看作True,缺失值看作False。
df.isnull()
| 花萼长度 | 花萼宽度 | 花瓣长度 | 花瓣宽度 | |
|---|---|---|---|---|
| False | True | False | False | |
| False | False | False | False | |
| False | False | True | False | |
| False | False | False | False | |
| False | False | False | False | |
| False | False | False | True | |
| True | True | True | True |
通过在isnull()方法后使用sum()方法即可获得该数据集某个特征含有多少个缺失值。
df.isnull().sum()
花萼长度 1
花萼宽度 2
花瓣长度 2
花瓣宽度 2
dtype: int64
2.1.1 删除缺失值
处理缺失值最简单也是最暴力的方法便是删除含有缺失值的样本或者特征(注:工业上数据非常重要,一般不推荐这样做),可以使用dropna()方法并通过它的参数axis选择删除样本还是特征,如果axis=1即删除特征;如果axis=0即删除行,how='all'删除所有特征全为缺失值的样本,thresh=4删除特征值数小于4的样本,subset=\\['花瓣宽度'\\]删除花瓣宽度特征中有缺失值的样本。
# axis=0删除有NaN值的行
df.dropna(axis=0)
| 花萼长度 | 花萼宽度 | 花瓣长度 | 花瓣宽度 | |
|---|---|---|---|---|
| 4.9 | 3.0 | 1.4 | 0.2 | |
| 7.0 | 3.2 | 4.7 | 1.4 | |
| 6.4 | 3.2 | 4.5 | 1.5 |
# axis=1删除有NaN值的列
df.dropna(axis=1)
# 删除全为NaN值得行或列
df.dropna(how='all')
| 花萼长度 | 花萼宽度 | 花瓣长度 | 花瓣宽度 | |
|---|---|---|---|---|
| 5.1 | NaN | 1.4 | 0.2 | |
| 4.9 | 3.0 | 1.4 | 0.2 | |
| 4.7 | 3.2 | NaN | 0.2 | |
| 7.0 | 3.2 | 4.7 | 1.4 | |
| 6.4 | 3.2 | 4.5 | 1.5 | |
| 6.9 | 3.1 | 4.9 | NaN |
# 删除行不为4个值的
df.dropna(thresh=4)
| 花萼长度 | 花萼宽度 | 花瓣长度 | 花瓣宽度 | |
|---|---|---|---|---|
| 4.9 | 3.0 | 1.4 | 0.2 | |
| 7.0 | 3.2 | 4.7 | 1.4 | |
| 6.4 | 3.2 | 4.5 | 1.5 |
# 删除花萼宽度中有NaN值的数据
df.dropna(subset=['花萼宽度'])
| 花萼长度 | 花萼宽度 | 花瓣长度 | 花瓣宽度 | |
|---|---|---|---|---|
| 4.9 | 3.0 | 1.4 | 0.2 | |
| 4.7 | 3.2 | NaN | 0.2 | |
| 7.0 | 3.2 | 4.7 | 1.4 | |
| 6.4 | 3.2 | 4.5 | 1.5 | |
| 6.9 | 3.1 | 4.9 | NaN |
2.1.2 填充缺失值
由于工业上的数据来之不易是很重要的,所以对缺失值的处理最常用的方法是填充缺失值。填充缺失值可以使用中位数、众数、平均数与自定义固定值,具体用哪一种没有硬性的要求,具体问题具体分析。本节将通过scikit-learn的Imputer给出填充平均值的方法。
# 填充缺失值示例
from sklearn.impute import SimpleImputer
import numpy as np
# 对所有缺失值填充固定值0
# imputer = SimpleImputer(missing_values=np.nan, strategy='constant', fill_value=0)
# 中位数strategy=median,众数strategy=most_frequent
imputer = SimpleImputer(missing_values=np.nan, strategy='mean')
imputer = imputer.fit(df.values)
imputed_data = imputer.transform(df.values)
imputed_data
array([[5.1 , 3.14 , 1.4 , 0.2 ],
[4.9 , 3. , 1.4 , 0.2 ],
[4.7 , 3.2 , 3.38 , 0.2 ],
[7. , 3.2 , 4.7 , 1.4 ],
[6.4 , 3.2 , 4.5 , 1.5 ],
[6.9 , 3.1 , 4.9 , 0.7 ],
[5.83333333, 3.14 , 3.38 , 0.7 ]])
2.2 离群值处理
离群值又称为异常值,即不合理的值。假设某个数据集有x1与x2两个特征,如下图所示:
# 离群值处理示例
import random
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')
x1 = [i for i in range(6)]
x2 = x1
plt.scatter(x1, x2, color='b', label='正常值')
plt.scatter(x1, [i+random.random() for i in x1.copy()] , color='b')
plt.scatter(1.5, 8, color='r', label='离群值')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend(prop=font)
# plt.savefig('img/离群值.png', dpi=300)
plt.show()
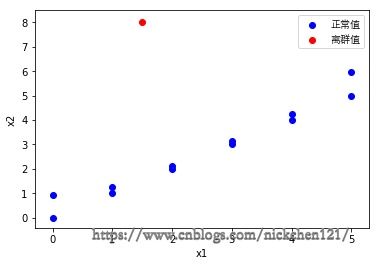
2.2.1 获取离群值
- 统计分析
对特征值统计后分析判断哪些值是不符合逻辑的,拿年龄举例,如果发现某个人的年龄是200,至少目前是不合理的,因此可以设定一个条件,把年龄大于200的数据都排除掉。 - 概率分布原则
根据高斯分布可知距离平均值\(3\delta\)之外的概率为0.003,这在统计学中属于极小概率事件,因此可以把超过该距离的值当作异常值处理。当然,你也可以手动设定这个距离或概率,具体问题具体分析。
2.2.2 离群值处理
往往可以用上述两种方法获取离群值,获取离群值之后的处理方式如同缺失值一样,可以把离群值设置为空值NaN,然后使用与处理缺失值同样的方法处理离群值,此处不多在赘述。
2.3 数据类型转换
现有一个汽车样本集,通过这个汽车样本集可以判断人们是否会购买该汽车。但是这个样本集的特征值是离散型的,为了确保计算机能正确读取该离散值的特征,需要给这些特征做编码处理,即创建一个映射表。如果特征值分类较少,可以选择自定义一个字典存放特征值与自定义值的关系。
car_data='''
乘坐人数,后备箱大小,安全性,是否可以接受
4,med,high,acc
2,big,low,unacc
4,big,med,acc
4,big,high,acc
6,small,low,unacc
6,small,med,unacc
'''
df = pd.read_csv(StringIO(car_data), header=0)
df
| 乘坐人数 | 后备箱大小 | 安全性 | 是否可以接受 | |
|---|---|---|---|---|
| 4 | med | high | acc | |
| 2 | big | low | unacc | |
| 4 | big | med | acc | |
| 4 | big | high | acc | |
| 6 | small | low | unacc | |
| 6 | small | med | unacc |
2.3.1 自定义数据类型编码
此处只拿汽车安全性(safety)举例。
safety_mapping = {
'low':0,
'med':1,
'high':2,
}
df['安全性'] = df['安全性'].map(safety_mapping)
df
| 乘坐人数 | 后备箱大小 | 安全性 | 是否可以接受 | |
|---|---|---|---|---|
| 4 | med | 2 | acc | |
| 2 | big | 0 | unacc | |
| 4 | big | 1 | acc | |
| 4 | big | 2 | acc | |
| 6 | small | 0 | unacc | |
| 6 | small | 1 | unacc |
对上述字典做反向映射处理,即可反向映射回原来的离散类型的特征值。
inverse_safety_mapping = {v: k for k, v in safety_mapping.items()}
df['安全性'].map(inverse_safety_mapping)
0 high
1 low
2 med
3 high
4 low
5 med
Name: 安全性, dtype: object
2.3.2 scikit-learn数据类型编码
目前LabelEncoder支持对一维数组进行编码,有兴趣的同学可以通过上述映射的写法自定义封装fit和transform方法写一个对多个特征编码的LabelEncoder。此处只对后备箱大小属性和是否可以接受标签信息做编码处理。
# scikit-learn数据类型编码示例
from sklearn.preprocessing import LabelEncoder
X_label_encoder = LabelEncoder()
X = df[['乘坐人数', '后备箱大小', '安全性']].values
X[:, 1] = X_label_encoder.fit_transform(X[:, 1])
X
array([[4, 1, 2],
[2, 0, 0],
[4, 0, 1],
[4, 0, 2],
[6, 2, 0],
[6, 2, 1]], dtype=object)
y_label_encoder = LabelEncoder()
y = y_label_encoder.fit_transform(df['是否可以接受'].values)
y
array([0, 1, 0, 0, 1, 1])
与字典映射同理,可以使用inverse_transform()方法对数据做反向映射处理。
y_label_encoder.inverse_transform(y)
array(['acc', 'unacc', 'acc', 'acc', 'unacc', 'unacc'], dtype=object)
2.3.3 独热编码
假设汽车安全性只是一个衡量标准,没有特定的顺序。但是计算机很有可能把这些\(0,1,2\)作一个特定排序或者因此区分它们的重要性,这个时候就得考虑创建一个二进制值分别表示low、med、high这三个属性值,有为1,没有为0,例如\(010\)表示为med。
scikit-learn中的OneHotEncoder可以实现这种编码处理。
# 独热编码示例
from sklearn.preprocessing import OneHotEncoder
one_hot_encoder = OneHotEncoder(categories='auto')
one_hot_encoder.fit_transform(X).toarray()
array([[0., 1., 0., 0., 1., 0., 0., 0., 1.],
[1., 0., 0., 1., 0., 0., 1., 0., 0.],
[0., 1., 0., 1., 0., 0., 0., 1., 0.],
[0., 1., 0., 1., 0., 0., 0., 0., 1.],
[0., 0., 1., 0., 0., 1., 1., 0., 0.],
[0., 0., 1., 0., 0., 1., 0., 1., 0.]])
使用categories对单个属性进行独热编码。
one_hot_encoder = OneHotEncoder(categories=[['med','big','small']])
# 可在OneHotEncoder类中加入sparseFale参数等同于toarray()方法
one_hot_encoder.fit_transform(df[['后备箱大小']]).toarray()
array([[1., 0., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 1., 0.],
[0., 0., 1.],
[0., 0., 1.]])
使用pandas对字符串属性独热编码,如果属性值为数值型则不进行独热编码。
pd.get_dummies(df[['乘坐人数', '后备箱大小', '安全性']])
| 乘坐人数 | 安全性 | 后备箱大小_big | 后备箱大小_med | 后备箱大小_small | |
|---|---|---|---|---|---|
| 4 | 2 | 0 | 1 | 0 | |
| 2 | 0 | 1 | 0 | 0 | |
| 4 | 1 | 1 | 0 | 0 | |
| 4 | 2 | 1 | 0 | 0 | |
| 6 | 0 | 0 | 0 | 1 | |
| 6 | 1 | 0 | 0 | 1 |
使用独热编码在解决特征值无序性的同时也增加了特征数,这无疑会给未来的计算增加难度,因此可以适当减少不必要的维度。例如当为后备箱进行独热编码的时候会有后备箱大小_big、后备箱大小_med、后备箱大小_small三个特征,可以减去一个特征,即后备箱大小_big与后备箱大小_med都为0则代表是后备箱大小_small。在调用pandas的get_dummies函数时,可以添加drop_first=True参数;而使用OneHotEncoder时得自己分隔。
pd.get_dummies(df[['乘坐人数', '后备箱大小', '安全性']],drop_first=True)
| 乘坐人数 | 安全性 | 后备箱大小_med | 后备箱大小_small | |
|---|---|---|---|---|
| 4 | 2 | 1 | 0 | |
| 2 | 0 | 0 | 0 | |
| 4 | 1 | 0 | 0 | |
| 4 | 2 | 0 | 0 | |
| 6 | 0 | 0 | 1 | |
| 6 | 1 | 0 | 1 |
one_hot_encoder = OneHotEncoder(categories=[['med','big','small']])
one_hot_encoder.fit_transform(df[['后备箱大小']]).toarray()[:, 1:]
array([[0., 0.],
[1., 0.],
[1., 0.],
[1., 0.],
[0., 1.],
[0., 1.]])
2.4 归一化数据
不同尺度特征可以这样理解,房价可能和房子面积与房间数有关并且假设两个特征具有相同的权重,但是现如今由于房子面积和房间数的度量单位是不同的,通常情况下房子面积的数值往往是远大于房间数数值的,那么称房子面积和房间数是不同尺度的。如果对这两个特征做处理,很有可能房子面积的影响会掩盖住房间数对房价造成的影响。
2.4.1 最小-最大标准化
为了解决相同权重特征不同尺度的问题,可以使用机器学习中的最小-最大标准化做处理,把他们两个值压缩在\([0-1]\)区间内。
最小-最大标准化公式:
其中\(i=1,2,\cdots,m\);\(m\)为样本个数;\(x_{min},x_{max}\)分别是某个的特征最小值和最大值。
# 最小最大标准化示例
from sklearn.preprocessing import MinMaxScaler
import numpy as np
test_data = np.array([1,2,3,4,5]).reshape(-1, 1).astype(float)
min_max_scaler = MinMaxScaler()
min_max_scaler.fit_transform(test_data)
array([[0. ],
[0.25],
[0.5 ],
[0.75],
[1. ]])
2.4.2 Z-score标准化
还有一种方法也可以对数据进行压缩,但是它的压缩并不能把数据限制在某个区间,它把数据压缩成类似高斯分布的分布方式,并且也能处理离群值对数据的影响。
在分类、聚类算法中,需要使用距离来度量相似性的时候应用非常好,尤其是数据本身呈正态分布的时候。
数据标准化公式:
使用标准化后,可以把特征列的中心设在均值为\(0\)且标准差为\(1\)的位置,即数据处理后特征列符合标准正态分布。
# Z-score标准化
from sklearn.preprocessing import StandardScaler
test_data = np.array([1,2,3,4,5]).reshape(-1, 1).astype(float)
standard_scaler = StandardScaler()
# fit_transform()=fit()+transform(), fit()方法估算平均值和方差,transform()方法对数据标准化
standard_scaler.fit_transform(test_data)
array([[-1.41421356],
[-0.70710678],
[ 0. ],
[ 0.70710678],
[ 1.41421356]])
2.5 二值化数据
数据二值化类似于独热编码,但是不同于独热编码的是它不是0就是1,即又有点类似于二分类,不卖关子。直接给出数据二值化的公式:
上述\(\theta\)是手动设置的阈值,如果特征值小于阈值为0;特征值大于阈值为1。
# 数据二值化示例
from sklearn.preprocessing import Binarizer
test_data = np.array([1,2,3,4,5]).reshape(-1, 1).astype(float)
binarizer = Binarizer(threshold=2.5)
binarizer.fit_transform(test_data)
array([[0.],
[0.],
[1.],
[1.],
[1.]])
2.6 正则化数据
正则化是将每个样本缩放到单位范数,即使得每个样本的p范数为1,对需要计算样本间相似度有很大的作用,通常有L1正则化和L2正则化两种方法。
# L1正则化示例
from sklearn.preprocessing import normalize
test_data = [[1, 2, 0, 4, 5], [2, 3, 4, 5, 9]]
normalize = normalize(test_data, norm='l1')
normalize
array([[0.08333333, 0.16666667, 0. , 0.33333333, 0.41666667],
[0.08695652, 0.13043478, 0.17391304, 0.2173913 , 0.39130435]])
# L2正则化示例
from sklearn.preprocessing import Normalizer
test_data = [[1, 2, 0, 4, 5], [2, 3, 4, 5, 9]]
normalize = Normalizer(norm='l2')
normalize = normalize.fit_transform(test_data)
normalize
array([[0.14744196, 0.29488391, 0. , 0.58976782, 0.73720978],
[0.17213259, 0.25819889, 0.34426519, 0.43033148, 0.77459667]])
2.7 生成多项式特征
# make_circles()示例
from sklearn import datasets
X1, y1 = datasets.make_circles(
n_samples=1000, random_state=1, factor=0.5, noise=0.1)
plt.scatter(0,0,s=23000,color='white',edgecolors='r')
plt.scatter(X1[:, 0], X1[:, 1], marker='*', c=y1)
plt.xlabel('$x_1$', fontsize=15)
plt.ylabel('$x_2$', fontsize=15)
plt.title('make_circles()', fontsize=20)
plt.show()
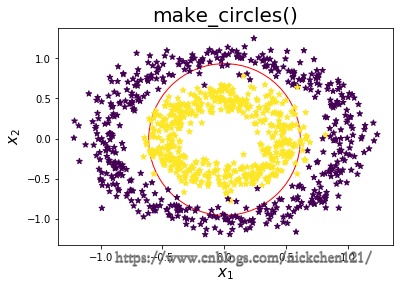
有时候可能会遇到上图所示的数据分布情况,如果这个时候使用简单的\(x_1,x_2\)特征去拟合曲线,明显是不可能的,但是我们可以使用,但是我们可以使用\(x_1^2+x_2^2=1\)去拟合数据,可能会得到一个较好的模型,所以我们有时候会对特征做一个多项式处理,即把特征\(x_1,x_2\)变成\(x_1^2,x_2^2\)。
test_data = [[1, 2], [3, 4], [5,6]]
test_data
[[1, 2], [3, 4], [5, 6]]
通过多项式特征,特征将会做如下变换
# 生成多项式特征示例
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures()
poly = poly.fit_transform(test_data)
poly
array([[ 1., 1., 2., 1., 2., 4.],
[ 1., 3., 4., 9., 12., 16.],
[ 1., 5., 6., 25., 30., 36.]])
三、小结
本问主要介绍了数据预处理的方法。但是现实生活中数据的数量以及复杂度远不是本文所介绍的如此简单,限于篇幅只能给你们做个引路人,但是对数据预处理的目标是不会变的,为了让算法更好的实现,实现的更好。如若只是数据中有脏数据,这些方法也够用了。
特征工程也算是告一段落了,但是特征工程远没有这两篇文章介绍的这么简单。特征工程也如其名,工程二字就说明了太多太多,特征工程更多的是在工作中或各类竞赛中的经验积累,他不如算法一样有固定的套路,也没有哪个人能说哪个数据处理的方法会比任何一个其他的数据处理的方法更优。
最后,还是送给大家那一句话:数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号