08-06 细分构建机器学习应用程序的流程-训练模型
目录
人工智能从入门到放弃完整教程目录:https://www.cnblogs.com/nickchen121/p/11686958.html
细分构建机器学习应用程序的流程-训练模型
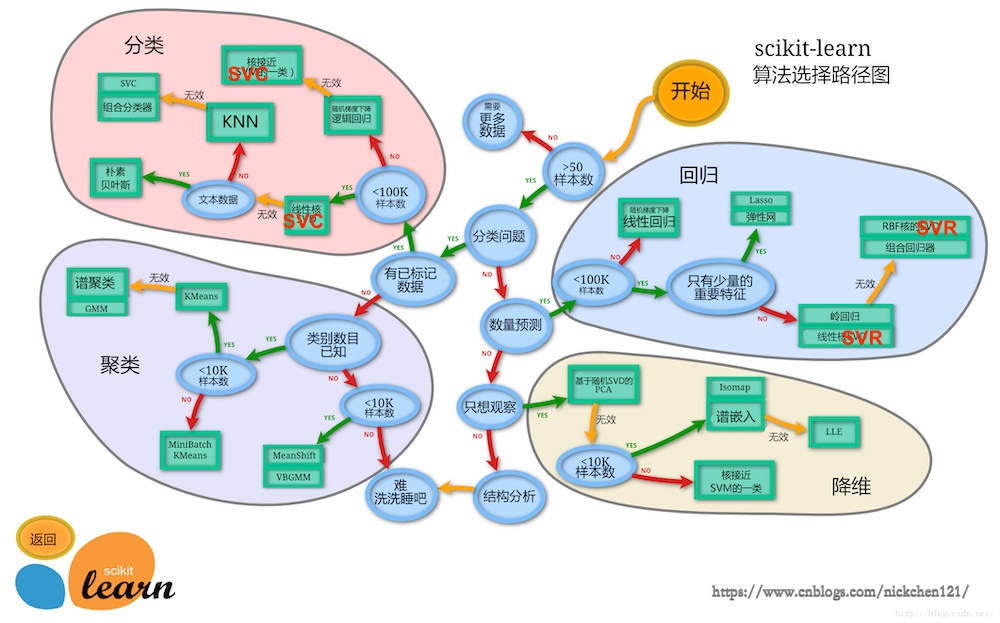
一、1.1 训练回归模型
接下来我们将用波士顿房价数据集来介绍我们的回归模型,波士顿总共有506条数据,所以样本数小于100K,依据地图可以先使用Lasso回归-弹性网络回归-岭回归-线性支持向量回归-核支持向量回归-决策树回归-随机森林回归
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
from sklearn import datasets
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')
# 设置numpy数组的元素的精度(位数)
np.set_printoptions(precision=4, suppress=True)
boston = datasets.load_boston()
len(boston.target)
506
X = boston.data
X[:5]
array([[ 0.0063, 18. , 2.31 , 0. , 0.538 , 6.575 ,
65.2 , 4.09 , 1. , 296. , 15.3 , 396.9 ,
4.98 ],
[ 0.0273, 0. , 7.07 , 0. , 0.469 , 6.421 ,
78.9 , 4.9671, 2. , 242. , 17.8 , 396.9 ,
9.14 ],
[ 0.0273, 0. , 7.07 , 0. , 0.469 , 7.185 ,
61.1 , 4.9671, 2. , 242. , 17.8 , 392.83 ,
4.03 ],
[ 0.0324, 0. , 2.18 , 0. , 0.458 , 6.998 ,
45.8 , 6.0622, 3. , 222. , 18.7 , 394.63 ,
2.94 ],
[ 0.0691, 0. , 2.18 , 0. , 0.458 , 7.147 ,
54.2 , 6.0622, 3. , 222. , 18.7 , 396.9 ,
5.33 ]])
y = boston.target
y
array([24. , 21.6, 34.7, 33.4, 36.2, 28.7, 22.9, 27.1, 16.5, 18.9, 15. ,
18.9, 21.7, 20.4, 18.2, 19.9, 23.1, 17.5, 20.2, 18.2, 13.6, 19.6,
15.2, 14.5, 15.6, 13.9, 16.6, 14.8, 18.4, 21. , 12.7, 14.5, 13.2,
13.1, 13.5, 18.9, 20. , 21. , 24.7, 30.8, 34.9, 26.6, 25.3, 24.7,
21.2, 19.3, 20. , 16.6, 14.4, 19.4, 19.7, 20.5, 25. , 23.4, 18.9,
35.4, 24.7, 31.6, 23.3, 19.6, 18.7, 16. , 22.2, 25. , 33. , 23.5,
19.4, 22. , 17.4, 20.9, 24.2, 21.7, 22.8, 23.4, 24.1, 21.4, 20. ,
20.8, 21.2, 20.3, 28. , 23.9, 24.8, 22.9, 23.9, 26.6, 22.5, 22.2,
23.6, 28.7, 22.6, 22. , 22.9, 25. , 20.6, 28.4, 21.4, 38.7, 43.8,
33.2, 27.5, 26.5, 18.6, 19.3, 20.1, 19.5, 19.5, 20.4, 19.8, 19.4,
21.7, 22.8, 18.8, 18.7, 18.5, 18.3, 21.2, 19.2, 20.4, 19.3, 22. ,
20.3, 20.5, 17.3, 18.8, 21.4, 15.7, 16.2, 18. , 14.3, 19.2, 19.6,
23. , 18.4, 15.6, 18.1, 17.4, 17.1, 13.3, 17.8, 14. , 14.4, 13.4,
15.6, 11.8, 13.8, 15.6, 14.6, 17.8, 15.4, 21.5, 19.6, 15.3, 19.4,
17. , 15.6, 13.1, 41.3, 24.3, 23.3, 27. , 50. , 50. , 50. , 22.7,
25. , 50. , 23.8, 23.8, 22.3, 17.4, 19.1, 23.1, 23.6, 22.6, 29.4,
23.2, 24.6, 29.9, 37.2, 39.8, 36.2, 37.9, 32.5, 26.4, 29.6, 50. ,
32. , 29.8, 34.9, 37. , 30.5, 36.4, 31.1, 29.1, 50. , 33.3, 30.3,
34.6, 34.9, 32.9, 24.1, 42.3, 48.5, 50. , 22.6, 24.4, 22.5, 24.4,
20. , 21.7, 19.3, 22.4, 28.1, 23.7, 25. , 23.3, 28.7, 21.5, 23. ,
26.7, 21.7, 27.5, 30.1, 44.8, 50. , 37.6, 31.6, 46.7, 31.5, 24.3,
31.7, 41.7, 48.3, 29. , 24. , 25.1, 31.5, 23.7, 23.3, 22. , 20.1,
22.2, 23.7, 17.6, 18.5, 24.3, 20.5, 24.5, 26.2, 24.4, 24.8, 29.6,
42.8, 21.9, 20.9, 44. , 50. , 36. , 30.1, 33.8, 43.1, 48.8, 31. ,
36.5, 22.8, 30.7, 50. , 43.5, 20.7, 21.1, 25.2, 24.4, 35.2, 32.4,
32. , 33.2, 33.1, 29.1, 35.1, 45.4, 35.4, 46. , 50. , 32.2, 22. ,
20.1, 23.2, 22.3, 24.8, 28.5, 37.3, 27.9, 23.9, 21.7, 28.6, 27.1,
20.3, 22.5, 29. , 24.8, 22. , 26.4, 33.1, 36.1, 28.4, 33.4, 28.2,
22.8, 20.3, 16.1, 22.1, 19.4, 21.6, 23.8, 16.2, 17.8, 19.8, 23.1,
21. , 23.8, 23.1, 20.4, 18.5, 25. , 24.6, 23. , 22.2, 19.3, 22.6,
19.8, 17.1, 19.4, 22.2, 20.7, 21.1, 19.5, 18.5, 20.6, 19. , 18.7,
32.7, 16.5, 23.9, 31.2, 17.5, 17.2, 23.1, 24.5, 26.6, 22.9, 24.1,
18.6, 30.1, 18.2, 20.6, 17.8, 21.7, 22.7, 22.6, 25. , 19.9, 20.8,
16.8, 21.9, 27.5, 21.9, 23.1, 50. , 50. , 50. , 50. , 50. , 13.8,
13.8, 15. , 13.9, 13.3, 13.1, 10.2, 10.4, 10.9, 11.3, 12.3, 8.8,
7.2, 10.5, 7.4, 10.2, 11.5, 15.1, 23.2, 9.7, 13.8, 12.7, 13.1,
12.5, 8.5, 5. , 6.3, 5.6, 7.2, 12.1, 8.3, 8.5, 5. , 11.9,
27.9, 17.2, 27.5, 15. , 17.2, 17.9, 16.3, 7. , 7.2, 7.5, 10.4,
8.8, 8.4, 16.7, 14.2, 20.8, 13.4, 11.7, 8.3, 10.2, 10.9, 11. ,
9.5, 14.5, 14.1, 16.1, 14.3, 11.7, 13.4, 9.6, 8.7, 8.4, 12.8,
10.5, 17.1, 18.4, 15.4, 10.8, 11.8, 14.9, 12.6, 14.1, 13. , 13.4,
15.2, 16.1, 17.8, 14.9, 14.1, 12.7, 13.5, 14.9, 20. , 16.4, 17.7,
19.5, 20.2, 21.4, 19.9, 19. , 19.1, 19.1, 20.1, 19.9, 19.6, 23.2,
29.8, 13.8, 13.3, 16.7, 12. , 14.6, 21.4, 23. , 23.7, 25. , 21.8,
20.6, 21.2, 19.1, 20.6, 15.2, 7. , 8.1, 13.6, 20.1, 21.8, 24.5,
23.1, 19.7, 18.3, 21.2, 17.5, 16.8, 22.4, 20.6, 23.9, 22. , 11.9])
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=1, shuffle=True)
print('训练集长度:{}'.format(len(y_train)), '测试集长度:{}'.format(len(y_test)))
scaler = MinMaxScaler()
scaler = scaler.fit(X_train)
X_train, X_test = scaler.transform(X_train), scaler.transform(X_test)
print('标准化后的训练数据:\n{}'.format(X_train[:5]))
print('标准化后的测试数据:\n{}'.format(X_test[:5]))
训练集长度:354 测试集长度:152
标准化后的训练数据:
[[0.0085 0. 0.2815 0. 0.3148 0.4576 0.5936 0.3254 0.1304 0.229
0.8936 1. 0.1802]
[0.0022 0.25 0.1712 0. 0.1399 0.4608 0.9298 0.5173 0.3043 0.1851
0.7553 0.9525 0.3507]
[0.1335 0. 0.6466 0. 0.5885 0.6195 0.9872 0.0208 1. 0.9141
0.8085 1. 0.5384]
[0.0003 0.75 0.0913 0. 0.0885 0.5813 0.1681 0.3884 0.087 0.124
0.6064 0.9968 0.0715]
[0.0619 0. 0.6466 0. 0.6852 0. 0.8713 0.044 1. 0.9141
0.8085 0.8936 0.1487]]
标准化后的测试数据:
[[0.0006 0.33 0.063 0. 0.179 0.63 0.684 0.1867 0.2609 0.0668
0.617 1. 0.16 ]
[0.0003 0.55 0.1217 0. 0.2037 0.6007 0.5362 0.4185 0.1739 0.3492
0.5319 1. 0.1504]
[0.003 0. 0.2364 0. 0.1296 0.4731 0.8457 0.4146 0.087 0.0878
0.5638 0.9895 0.471 ]
[0.0007 0.125 0.2056 0. 0.0494 0.444 0.1638 0.4882 0.1304 0.3015
0.6702 0.9983 0.1758]
[0.0499 0. 0.6466 0. 0.7922 0.3451 0.9596 0.0886 1. 0.9141
0.8085 0.9594 0.2334]]
1.1 1.1.1 Lasso回归
from sklearn.linear_model import Lasso
# Lasso回归相当于在普通线性回归中加上了L1正则化项
reg = Lasso()
reg = reg.fit(X_train, y_train)
y_pred = reg.predict(X_test)
print('所有样本误差率:\n{}'.format(np.abs(y_pred/y_test-1)))
'Lasso回归R2分数:{}'.format(reg.score(X_test, y_test))
所有样本误差率:
[0.1634 0.0095 0.2647 0.0664 0.1048 0.0102 0.131 0.5394 0.0141 0.0309
0.0066 0.2222 0.1498 0.1839 0.1663 0.1924 0.4366 0.5148 0.0201 0.2684
0.3998 0.3775 0.0257 0.0433 0.032 1.374 0.5287 0.3086 0.4512 0.7844
0.0015 0.139 0.5067 0.7093 0.1734 0.0941 0.4246 0.3343 0.6761 0.1453
0.0459 0.1484 0.2167 0.4865 0.4501 1.391 0.5023 0.6975 0.0773 0.23
0.2403 0.0244 0.1593 0.0433 1.2819 0.071 1.9233 0.0837 0.254 0.4944
0.3093 0.1044 1.4394 0.4663 0.2188 0.3503 0.4062 0.4142 0.0567 0.0024
0.0396 0.7911 0.0091 0.0746 0.0823 0.0517 0.5071 0.0651 0.0139 0.3429
0.21 0.1955 0.3098 0.4897 0.0459 0.0748 0.6058 0.018 0.2064 0.1833
0.0054 0.517 0.556 0.0191 1.0166 0.1782 0.0312 0.0239 0.4559 0.0291
1.1285 0.3624 0.0518 0.0192 1.531 0.0605 0.8266 0.1089 0.2467 0.1109
0.4345 0.0151 0.8514 0.2863 0.3463 0.3223 0.2149 0.1205 0.2873 0.5277
0.1933 0.4103 0.0897 0.1084 0.0671 0.0542 0.023 0.1279 0.0502 0.139
0.1033 0.0069 0.0441 1.0007 0.0099 0.3426 0.4286 0.6492 0.4074 1.0538
0.1672 0.1838 0.0782 0.0069 0.1382 0.0446 0.0055 0.0687 0.1621 0.0338
0.316 0.4306]
'Lasso回归R2分数:0.21189040113362279'
1.2 1.1.2 弹性网络回归
from sklearn.linear_model import ElasticNet
# 弹性网络回归相当于在普通线性回归中加上了加权的(L1正则化项+L2正则化项)
reg = ElasticNet()
reg = reg.fit(X_train, y_train)
y_pred = reg.predict(X_test)
'弹性网络回归R2分数:{}'.format(reg.score(X_test, y_test))
'弹性网络回归R2分数:0.1414319491120538'
1.3 1.1.3 岭回归
from sklearn.linear_model import Ridge
# 岭回归相当于在普通线性回归中加上了L2正则化项
reg = Ridge()
reg = reg.fit(X_train, y_train)
y_pred = reg.predict(X_test)
'岭回归R2分数:{}'.format(reg.score(X_test, y_test))
'岭回归R2分数:0.7718570925003422'
1.4 1.1.4 线性支持向量回归
from sklearn.svm import LinearSVR
# 线性支持向量回归使用的是硬间隔最大化,可以处理异常值导致的数据线性不可分
reg = LinearSVR(C=100, max_iter=10000)
reg = reg.fit(X_train, y_train)
y_pred = reg.predict(X_test)
'线性支持向量回归R2分数:{}'.format(reg.score(X_test, y_test))
'线性支持向量回归R2分数:0.7825143888611817'
1.5 1.1.5 核支持向量回归
from sklearn.svm import SVR
# 核支持向量回归可以处理非线性可分数据
# 高斯核有参数C和gamma
reg = SVR(C=100, gamma='auto', max_iter=10000, kernel='rbf')
reg = reg.fit(X_train, y_train)
y_pred = reg.predict(X_test)
'核支持向量回归R2分数:{}'.format(reg.score(X_test, y_test))
'核支持向量回归R2分数:0.8315189988955631'
1.6 1.1.6 决策树回归
from sklearn.tree import DecisionTreeRegressor
# 使用的CART树
reg = DecisionTreeRegressor()
reg = reg.fit(X_train, y_train)
y_pred = reg.predict(X_test)
'决策树回归R2分数:{}'.format(reg.score(X_test, y_test))
'决策树回归R2分数:0.821739712044748'
1.7 1.1.7 随机森林回归
from sklearn.ensemble import RandomForestRegressor
# 随机森林属于集成学习中的Bagging算法
reg = RandomForestRegressor(n_estimators=100)
reg = reg.fit(X_train, y_train)
y_pred = reg.predict(X_test)
'随机森林回归R2分数:{}'.format(reg.score(X_test, y_test))
'随机森林回归R2分数:0.901713187504369'
二、1.2 训练分类模型
接下来我们将用乳腺癌数据集来介绍我们的分类模型,乳腺癌数据集总共有569条数据,所以样本数小于100K,依据地图可以先使用线性可分支持向量机-KNN算法-线性支持向量机-决策树分类-随机森林分类
import numpy as np
from sklearn import datasets
breast = datasets.load_breast_cancer()
len(breast.target)
569
X = breast.data
X[:5]
array([[ 17.99 , 10.38 , 122.8 , 1001. , 0.1184, 0.2776,
0.3001, 0.1471, 0.2419, 0.0787, 1.095 , 0.9053,
8.589 , 153.4 , 0.0064, 0.049 , 0.0537, 0.0159,
0.03 , 0.0062, 25.38 , 17.33 , 184.6 , 2019. ,
0.1622, 0.6656, 0.7119, 0.2654, 0.4601, 0.1189],
[ 20.57 , 17.77 , 132.9 , 1326. , 0.0847, 0.0786,
0.0869, 0.0702, 0.1812, 0.0567, 0.5435, 0.7339,
3.398 , 74.08 , 0.0052, 0.0131, 0.0186, 0.0134,
0.0139, 0.0035, 24.99 , 23.41 , 158.8 , 1956. ,
0.1238, 0.1866, 0.2416, 0.186 , 0.275 , 0.089 ],
[ 19.69 , 21.25 , 130. , 1203. , 0.1096, 0.1599,
0.1974, 0.1279, 0.2069, 0.06 , 0.7456, 0.7869,
4.585 , 94.03 , 0.0062, 0.0401, 0.0383, 0.0206,
0.0225, 0.0046, 23.57 , 25.53 , 152.5 , 1709. ,
0.1444, 0.4245, 0.4504, 0.243 , 0.3613, 0.0876],
[ 11.42 , 20.38 , 77.58 , 386.1 , 0.1425, 0.2839,
0.2414, 0.1052, 0.2597, 0.0974, 0.4956, 1.156 ,
3.445 , 27.23 , 0.0091, 0.0746, 0.0566, 0.0187,
0.0596, 0.0092, 14.91 , 26.5 , 98.87 , 567.7 ,
0.2098, 0.8663, 0.6869, 0.2575, 0.6638, 0.173 ],
[ 20.29 , 14.34 , 135.1 , 1297. , 0.1003, 0.1328,
0.198 , 0.1043, 0.1809, 0.0588, 0.7572, 0.7813,
5.438 , 94.44 , 0.0115, 0.0246, 0.0569, 0.0188,
0.0176, 0.0051, 22.54 , 16.67 , 152.2 , 1575. ,
0.1374, 0.205 , 0.4 , 0.1625, 0.2364, 0.0768]])
y = breast.target
y
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0,
0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0,
1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0,
1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1,
1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0,
0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1,
1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1,
1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0,
0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0,
1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1,
1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0,
0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0,
0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0,
1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1,
1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1,
1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0,
1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1,
1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1,
1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1])
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=1, shuffle=True)
print('训练集长度:{}'.format(len(y_train)), '测试集长度:{}'.format(len(y_test)))
训练集长度:398 测试集长度:171
2.1 1.2.1 线性可分支持向量机
from sklearn.svm import LinearSVC
clf = LinearSVC(C=1, max_iter=200000, tol=0.1)
clf = clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
'线性可分支持向量机分类准确率:{}'.format(clf.score(X_test, y_test))
/Applications/anaconda3/lib/python3.7/site-packages/sklearn/svm/base.py:922: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
"the number of iterations.", ConvergenceWarning)
'线性可分支持向量机分类准确率:0.7953216374269005'
2.2 1.2.2 KNN算法
from sklearn.neighbors import KNeighborsClassifier
# algorithm='kd_tree'表示使用的kd树搜索
clf = KNeighborsClassifier(algorithm='kd_tree')
clf = clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
'KNN算法准确率:{}'.format(clf.score(X_test, y_test))
'KNN算法准确率:0.9298245614035088'
2.3 1.2.3 核支持向量机
from sklearn.svm import SVC
# 线性支持向量机使用的是软间隔最大化,可以处理异常值导致的数据线性不可分
clf = SVC(C=10, gamma='auto', kernel='rbf')
clf = clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
'线性支持向量机分类准确率:{}'.format(clf.score(X_test, y_test))
'线性支持向量机分类准确率:0.631578947368421'
2.4 1.2.4 决策树分类
from sklearn.tree import DecisionTreeClassifier
# 使用的是CART树
reg = DecisionTreeClassifier()
reg = reg.fit(X_train, y_train)
y_pred = reg.predict(X_test)
'决策树分类准确率:{}'.format(reg.score(X_test, y_test))
'决策树分类准确率:0.9415204678362573'
2.5 1.2.5 随机森林分类
from sklearn.ensemble import RandomForestClassifier
# 使用的集成学习的Bagging算法集成决策树
reg = RandomForestClassifier(n_estimators=100)
reg = reg.fit(X_train, y_train)
y_pred = reg.predict(X_test)
'随机森林分类准确率:{}'.format(reg.score(X_test, y_test))
'随机森林分类准确率:0.9532163742690059'
三、1.3 训练聚类模型
聚类就不按照地图走了,此处只讲解最常用的k均值聚类算法。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
from sklearn import datasets
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')
# 生成3个簇的中心点
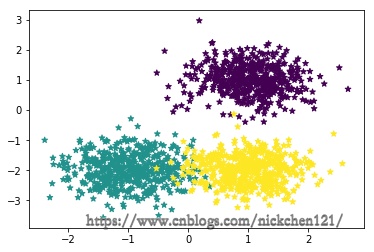
centers = [[1, 1], [-1, -2], [1, -2]]
X1, y1 = datasets.make_blobs(
n_samples=1500, centers=centers, n_features=2, random_state=1, shuffle=False, cluster_std=0.5)
plt.scatter(X1[:, 0], X1[:, 1], marker='*', c=y1)
plt.show()
from sklearn.cluster import KMeans
clt = KMeans(n_clusters=3, random_state=1)
clt.fit(X1)
clt.predict(X1)
array([1, 1, 1, ..., 0, 0, 0], dtype=int32)
cluster_centers = clt.cluster_centers_
cluster_centers
array([[ 0.9876, -2.0131],
[ 1.0229, 1.0131],
[-0.9967, -1.9877]])
centers = [[1, 1], [-1, -2], [1, -2]]
X1, y1 = datasets.make_blobs(
n_samples=1500, centers=centers, n_features=2, random_state=1, shuffle=False, cluster_std=0.5)
plt.scatter(X1[:, 0], X1[:, 1], marker='*', c=y1, alpha=0.3)
plt.scatter(cluster_centers[:, 0], cluster_centers[:, 1],
s=100, color='r', label='簇中心')
plt.legend(prop=font)
plt.show()

四、1.4 训练降维模型
# 维数灾难和降维图例
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
from sklearn.decomposition import PCA
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')
np.random.seed(0)
X = np.empty((100, 2))
X[:, 0] = np.random.uniform(0, 100, size=100)
X[:, 1] = 0.75 * X[:, 0] + 3. + np.random.normal(0, 10, size=100)
pca = PCA(n_components=1)
X_reduction = pca.fit_transform(X)
X_restore = pca.inverse_transform(X_reduction)
plt.scatter(X[:, 0], X[:, 1], color='g', label='原始数据')
plt.scatter(X_restore[:, 0], X_restore[:, 1],
color='r', label='降维后的数据')
plt.legend(prop=font)
plt.show()

降维算法曾在第三部分讲过,为了解决维数灾难,把高维数据压缩到低维空间,虽然解决了维数灾难这个问题,但数据在压缩的过程中也会丢失一部分信息,即会导致算法准确度会下降。也就是说降维算法更多的是拿时间换准确度,两者的权衡往往需要通过偏差度量。
import numpy as np
from sklearn import datasets
boston = datasets.load_boston()
feature_names = boston.feature_names
print('波士顿房价数据集特征:\n{}'.format(feature_names))
print('波士顿房价数据集特征个数:{}'.format(len(feature_names)))
波士顿房价数据集特征:
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
'B' 'LSTAT']
波士顿房价数据集特征个数:13
X = boston.data
X[:5]
array([[ 0.0063, 18. , 2.31 , 0. , 0.538 , 6.575 ,
65.2 , 4.09 , 1. , 296. , 15.3 , 396.9 ,
4.98 ],
[ 0.0273, 0. , 7.07 , 0. , 0.469 , 6.421 ,
78.9 , 4.9671, 2. , 242. , 17.8 , 396.9 ,
9.14 ],
[ 0.0273, 0. , 7.07 , 0. , 0.469 , 7.185 ,
61.1 , 4.9671, 2. , 242. , 17.8 , 392.83 ,
4.03 ],
[ 0.0324, 0. , 2.18 , 0. , 0.458 , 6.998 ,
45.8 , 6.0622, 3. , 222. , 18.7 , 394.63 ,
2.94 ],
[ 0.0691, 0. , 2.18 , 0. , 0.458 , 7.147 ,
54.2 , 6.0622, 3. , 222. , 18.7 , 396.9 ,
5.33 ]])
y = boston.target
y
array([24. , 21.6, 34.7, 33.4, 36.2, 28.7, 22.9, 27.1, 16.5, 18.9, 15. ,
18.9, 21.7, 20.4, 18.2, 19.9, 23.1, 17.5, 20.2, 18.2, 13.6, 19.6,
15.2, 14.5, 15.6, 13.9, 16.6, 14.8, 18.4, 21. , 12.7, 14.5, 13.2,
13.1, 13.5, 18.9, 20. , 21. , 24.7, 30.8, 34.9, 26.6, 25.3, 24.7,
21.2, 19.3, 20. , 16.6, 14.4, 19.4, 19.7, 20.5, 25. , 23.4, 18.9,
35.4, 24.7, 31.6, 23.3, 19.6, 18.7, 16. , 22.2, 25. , 33. , 23.5,
19.4, 22. , 17.4, 20.9, 24.2, 21.7, 22.8, 23.4, 24.1, 21.4, 20. ,
20.8, 21.2, 20.3, 28. , 23.9, 24.8, 22.9, 23.9, 26.6, 22.5, 22.2,
23.6, 28.7, 22.6, 22. , 22.9, 25. , 20.6, 28.4, 21.4, 38.7, 43.8,
33.2, 27.5, 26.5, 18.6, 19.3, 20.1, 19.5, 19.5, 20.4, 19.8, 19.4,
21.7, 22.8, 18.8, 18.7, 18.5, 18.3, 21.2, 19.2, 20.4, 19.3, 22. ,
20.3, 20.5, 17.3, 18.8, 21.4, 15.7, 16.2, 18. , 14.3, 19.2, 19.6,
23. , 18.4, 15.6, 18.1, 17.4, 17.1, 13.3, 17.8, 14. , 14.4, 13.4,
15.6, 11.8, 13.8, 15.6, 14.6, 17.8, 15.4, 21.5, 19.6, 15.3, 19.4,
17. , 15.6, 13.1, 41.3, 24.3, 23.3, 27. , 50. , 50. , 50. , 22.7,
25. , 50. , 23.8, 23.8, 22.3, 17.4, 19.1, 23.1, 23.6, 22.6, 29.4,
23.2, 24.6, 29.9, 37.2, 39.8, 36.2, 37.9, 32.5, 26.4, 29.6, 50. ,
32. , 29.8, 34.9, 37. , 30.5, 36.4, 31.1, 29.1, 50. , 33.3, 30.3,
34.6, 34.9, 32.9, 24.1, 42.3, 48.5, 50. , 22.6, 24.4, 22.5, 24.4,
20. , 21.7, 19.3, 22.4, 28.1, 23.7, 25. , 23.3, 28.7, 21.5, 23. ,
26.7, 21.7, 27.5, 30.1, 44.8, 50. , 37.6, 31.6, 46.7, 31.5, 24.3,
31.7, 41.7, 48.3, 29. , 24. , 25.1, 31.5, 23.7, 23.3, 22. , 20.1,
22.2, 23.7, 17.6, 18.5, 24.3, 20.5, 24.5, 26.2, 24.4, 24.8, 29.6,
42.8, 21.9, 20.9, 44. , 50. , 36. , 30.1, 33.8, 43.1, 48.8, 31. ,
36.5, 22.8, 30.7, 50. , 43.5, 20.7, 21.1, 25.2, 24.4, 35.2, 32.4,
32. , 33.2, 33.1, 29.1, 35.1, 45.4, 35.4, 46. , 50. , 32.2, 22. ,
20.1, 23.2, 22.3, 24.8, 28.5, 37.3, 27.9, 23.9, 21.7, 28.6, 27.1,
20.3, 22.5, 29. , 24.8, 22. , 26.4, 33.1, 36.1, 28.4, 33.4, 28.2,
22.8, 20.3, 16.1, 22.1, 19.4, 21.6, 23.8, 16.2, 17.8, 19.8, 23.1,
21. , 23.8, 23.1, 20.4, 18.5, 25. , 24.6, 23. , 22.2, 19.3, 22.6,
19.8, 17.1, 19.4, 22.2, 20.7, 21.1, 19.5, 18.5, 20.6, 19. , 18.7,
32.7, 16.5, 23.9, 31.2, 17.5, 17.2, 23.1, 24.5, 26.6, 22.9, 24.1,
18.6, 30.1, 18.2, 20.6, 17.8, 21.7, 22.7, 22.6, 25. , 19.9, 20.8,
16.8, 21.9, 27.5, 21.9, 23.1, 50. , 50. , 50. , 50. , 50. , 13.8,
13.8, 15. , 13.9, 13.3, 13.1, 10.2, 10.4, 10.9, 11.3, 12.3, 8.8,
7.2, 10.5, 7.4, 10.2, 11.5, 15.1, 23.2, 9.7, 13.8, 12.7, 13.1,
12.5, 8.5, 5. , 6.3, 5.6, 7.2, 12.1, 8.3, 8.5, 5. , 11.9,
27.9, 17.2, 27.5, 15. , 17.2, 17.9, 16.3, 7. , 7.2, 7.5, 10.4,
8.8, 8.4, 16.7, 14.2, 20.8, 13.4, 11.7, 8.3, 10.2, 10.9, 11. ,
9.5, 14.5, 14.1, 16.1, 14.3, 11.7, 13.4, 9.6, 8.7, 8.4, 12.8,
10.5, 17.1, 18.4, 15.4, 10.8, 11.8, 14.9, 12.6, 14.1, 13. , 13.4,
15.2, 16.1, 17.8, 14.9, 14.1, 12.7, 13.5, 14.9, 20. , 16.4, 17.7,
19.5, 20.2, 21.4, 19.9, 19. , 19.1, 19.1, 20.1, 19.9, 19.6, 23.2,
29.8, 13.8, 13.3, 16.7, 12. , 14.6, 21.4, 23. , 23.7, 25. , 21.8,
20.6, 21.2, 19.1, 20.6, 15.2, 7. , 8.1, 13.6, 20.1, 21.8, 24.5,
23.1, 19.7, 18.3, 21.2, 17.5, 16.8, 22.4, 20.6, 23.9, 22. , 11.9])
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=1, shuffle=True)
print('训练集长度:{}'.format(len(y_train)), '测试集长度:{}'.format(len(y_test)))
scaler = MinMaxScaler()
scaler = scaler.fit(X_train)
X_train, X_test = scaler.transform(X_train), scaler.transform(X_test)
训练集长度:354 测试集长度:152
from sklearn.decomposition import PCA
pca = PCA(n_components=8, random_state=1)
pca.fit(X_train)
PCA(copy=True, iterated_power='auto', n_components=8, random_state=1,
svd_solver='auto', tol=0.0, whiten=False)
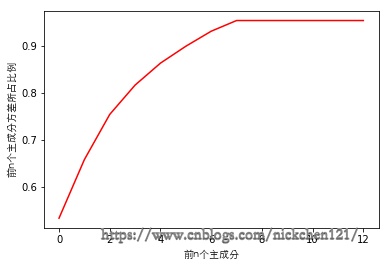
pca.explained_variance_
array([0.432, 0.101, 0.078, 0.051, 0.038, 0.029, 0.026, 0.018])
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')
plt.plot([i for i in range(X_train.shape[1])],
[np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])], c='r')
plt.xlabel('前n个主成分', fontproperties=font)
plt.ylabel('前n个主成分方差所占比例', fontproperties=font)
plt.show()
from sklearn.ensemble import RandomForestRegressor
print('主成分个数:{}'.format(pca.n_components))
X_train_reduction, X_test_reduction = pca.transform(
X_train), pca.transform(X_test)
reg = RandomForestRegressor(n_estimators=100)
reg = reg.fit(X_train_reduction, y_train)
'随机森林回归R2分数:{}'.format(reg.score(X_test_reduction, y_test))
主成分个数:8
'随机森林回归R2分数:0.7991016859462761'
from sklearn.ensemble import RandomForestRegressor
pca = PCA(n_components=4, random_state=1)
pca.fit(X_train)
print('主成分个数:{}'.format(pca.n_components))
X_train_reduction, X_test_reduction = pca.transform(
X_train), pca.transform(X_test)
reg = RandomForestRegressor(n_estimators=100)
reg = reg.fit(X_train_reduction, y_train)
'随机森林回归R2分数:{}'.format(reg.score(X_test_reduction, y_test))
主成分个数:4
'随机森林回归R2分数:0.6906787832916879'
from sklearn.ensemble import RandomForestRegressor
pca = PCA(n_components=11, random_state=1)
pca.fit(X_train)
print('主成分个数:{}'.format(pca.n_components))
X_train_reduction, X_test_reduction = pca.transform(
X_train), pca.transform(X_test)
reg = RandomForestRegressor(n_estimators=100)
reg = reg.fit(X_train_reduction, y_train)
'随机森林回归R2分数:{}'.format(reg.score(X_test_reduction, y_test))
主成分个数:11
'随机森林回归R2分数:0.8067610472904356'
五、1.5 管道训练
管道训练相当于工厂流水线,在这个流水线中会有多个估计器,并且每一个估计器的输入都源自于上一个估计器的输出,需要注意的是管道机制更像是编程技巧的创新,而非算法的创新。
管道中最常用的是如下所示的流水线,第一个估计器做数据预处理,第二个估计器做降维处理,第三个估计器做分类、回归或者聚类。
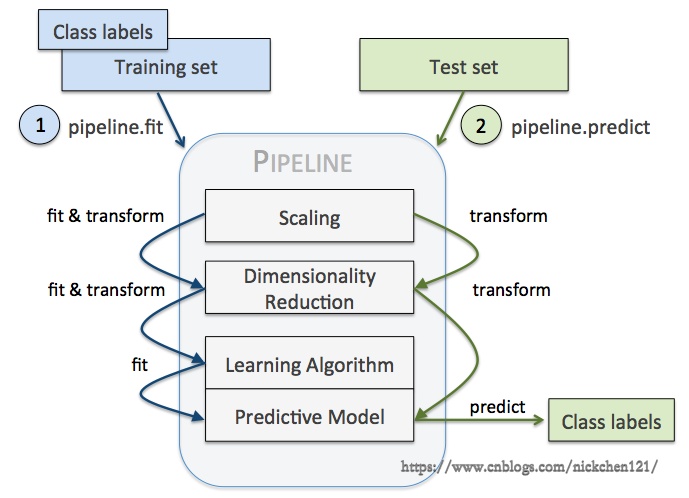
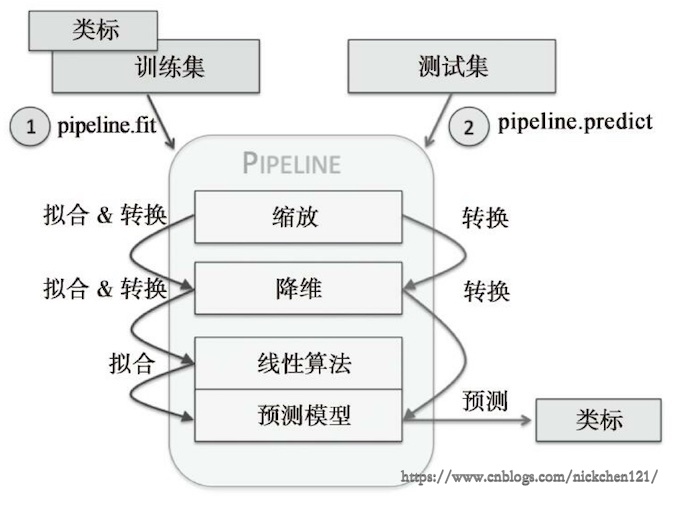
上图就是我们最常用的管道训练的一个流程,但是需要注意的是:
- 只有最后一个估计器可以为转换器(transform)或分类器(classifer)、回归器、聚类器
- 除了最后一个估计器之外,其他的估计器必须为转换器
- 最优一个估计器为转换器,管道为估计器;最后一个估计器为分类器,管道为分类器,即管道可以使用网格搜索法优化模型
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from sklearn.decomposition import PCA
from sklearn.ensemble import RandomForestRegressor
from sklearn.pipeline import Pipeline
boston = datasets.load_boston()
X = boston.data
y = boston.target
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=1, shuffle=True)
print('训练集长度:{}'.format(len(y_train)), '测试集长度:{}'.format(len(y_test)))
scaler = MinMaxScaler()
scaler = scaler.fit(X_train)
X_train, X_test = scaler.transform(X_train), scaler.transform(X_test)
pipe = Pipeline([('scaler', MinMaxScaler()), ('pca', PCA()),
('rfreg', RandomForestRegressor())])
pipe.get_params()
训练集长度:354 测试集长度:152
{'memory': None,
'steps': [('scaler', MinMaxScaler(copy=True, feature_range=(0, 1))),
('pca',
PCA(copy=True, iterated_power='auto', n_components=None, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)),
('rfreg',
RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators='warn', n_jobs=None,
oob_score=False, random_state=None, verbose=0, warm_start=False))],
'scaler': MinMaxScaler(copy=True, feature_range=(0, 1)),
'pca': PCA(copy=True, iterated_power='auto', n_components=None, random_state=None,
svd_solver='auto', tol=0.0, whiten=False),
'rfreg': RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators='warn', n_jobs=None,
oob_score=False, random_state=None, verbose=0, warm_start=False),
'scaler__copy': True,
'scaler__feature_range': (0, 1),
'pca__copy': True,
'pca__iterated_power': 'auto',
'pca__n_components': None,
'pca__random_state': None,
'pca__svd_solver': 'auto',
'pca__tol': 0.0,
'pca__whiten': False,
'rfreg__bootstrap': True,
'rfreg__criterion': 'mse',
'rfreg__max_depth': None,
'rfreg__max_features': 'auto',
'rfreg__max_leaf_nodes': None,
'rfreg__min_impurity_decrease': 0.0,
'rfreg__min_impurity_split': None,
'rfreg__min_samples_leaf': 1,
'rfreg__min_samples_split': 2,
'rfreg__min_weight_fraction_leaf': 0.0,
'rfreg__n_estimators': 'warn',
'rfreg__n_jobs': None,
'rfreg__oob_score': False,
'rfreg__random_state': None,
'rfreg__verbose': 0,
'rfreg__warm_start': False}
pipe.set_params(pca__n_components=10, rfreg__n_estimators=100)
pipe.get_params()
{'memory': None,
'steps': [('scaler', MinMaxScaler(copy=True, feature_range=(0, 1))),
('pca',
PCA(copy=True, iterated_power='auto', n_components=10, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)),
('rfreg',
RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100, n_jobs=None,
oob_score=False, random_state=None, verbose=0, warm_start=False))],
'scaler': MinMaxScaler(copy=True, feature_range=(0, 1)),
'pca': PCA(copy=True, iterated_power='auto', n_components=10, random_state=None,
svd_solver='auto', tol=0.0, whiten=False),
'rfreg': RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100, n_jobs=None,
oob_score=False, random_state=None, verbose=0, warm_start=False),
'scaler__copy': True,
'scaler__feature_range': (0, 1),
'pca__copy': True,
'pca__iterated_power': 'auto',
'pca__n_components': 10,
'pca__random_state': None,
'pca__svd_solver': 'auto',
'pca__tol': 0.0,
'pca__whiten': False,
'rfreg__bootstrap': True,
'rfreg__criterion': 'mse',
'rfreg__max_depth': None,
'rfreg__max_features': 'auto',
'rfreg__max_leaf_nodes': None,
'rfreg__min_impurity_decrease': 0.0,
'rfreg__min_impurity_split': None,
'rfreg__min_samples_leaf': 1,
'rfreg__min_samples_split': 2,
'rfreg__min_weight_fraction_leaf': 0.0,
'rfreg__n_estimators': 100,
'rfreg__n_jobs': None,
'rfreg__oob_score': False,
'rfreg__random_state': None,
'rfreg__verbose': 0,
'rfreg__warm_start': False}
pipe.fit(X_test, y_test)
y_pred = pipe.predict(X_test)
print('所有样本误差率:\n{}'.format(np.abs(y_pred/y_test-1)))
所有样本误差率:
[0. 0.022 0.083 0.026 0.012 0.067 0.02 0.113 0. 0.017 0.087 0.03
0.04 0.08 0.041 0.136 0.095 0.035 0.038 0.05 0.134 0.088 0.039 0.024
0.029 0.142 0.11 0.067 0.032 0.042 0.04 0.003 0.089 0.143 0.021 0.05
0.032 0.055 0.065 0.003 0.003 0.026 0.052 0.006 0.069 0.151 0.102 0.126
0.014 0.111 0.107 0.035 0.001 0.014 0.312 0.009 0.183 0.022 0.028 0.076
0.001 0.041 0.197 0.004 0.015 0.015 0.004 0.114 0.018 0.01 0.033 0.083
0.1 0.05 0.004 0.051 0.153 0.023 0.03 0.093 0.025 0.032 0.027 0.074
0.029 0.091 0.033 0.003 0.044 0.006 0.098 0.031 0.165 0.03 0.308 0.047
0.007 0.022 0.01 0.007 0.267 0.1 0.005 0.001 0.096 0.045 0.039 0.149
0.103 0.027 0.008 0.004 0.02 0.014 0.087 0.084 0.047 0.036 0.055 0.04
0.043 0.03 0.003 0.002 0.006 0.011 0.016 0.002 0.057 0.031 0.046 0.011
0.009 0.045 0.005 0.086 0.174 0.028 0.047 0.167 0.063 0.002 0.038 0.045
0.049 0.033 0.009 0.081 0. 0.012 0.021 0.053]
'管道回归R2分数:{}'.format(pipe.score(X_test, y_test))
'管道回归R2分数:0.9728609036046043'
六、1.6 特征联合
特征联合类似于管道训练,但是与管道训练有以下两个不同之处:
- 管道训练是串联;特征联合是并联
- 管道训练最后一个估计器可以是分类器、回归器、聚类器;特征联合所有的估计器只能是转换器
from sklearn import datasets
from sklearn.pipeline import FeatureUnion
from sklearn.decomposition import PCA
from sklearn.decomposition import KernelPCA
boston = datasets.load_boston()
X = boston.data
print('波士顿房价特征维度:{}'.format(X.shape))
# KernelPCA()可以类似于核支持向量机,可以把数据映射到高维
feature_union = FeatureUnion(
[('linear_pca', PCA(n_components=4)), ('kernel_pca', KernelPCA(n_components=18))])
feature_union.fit_transform(X).shape
波士顿房价特征维度:(506, 13)
(506, 22)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号