小白专场-是否同一颗二叉搜索树-c语言实现
数据结构与算法_Python_C完整教程目录:https://www.cnblogs.com/nickchen121/p/11407287.html
更新、更全的《数据结构与算法》的更新网站,更有python、go、人工智能教学等着你:https://www.cnblogs.com/nickchen121/p/11407287.html
一、题意理解
给定一个插入序列就可以唯一确定一颗二叉搜索树。然而,一颗给定的二叉搜索树却可以由多种不同的插入序列得到。例如:按照序列 {2, 1, 3} 和 {2, 3, 1}插入初始为空的二叉搜索树,都得到一样的结果。
问题:对于输入的各种插入序列,你需要判断它们是否能生成一样的二叉搜索树。
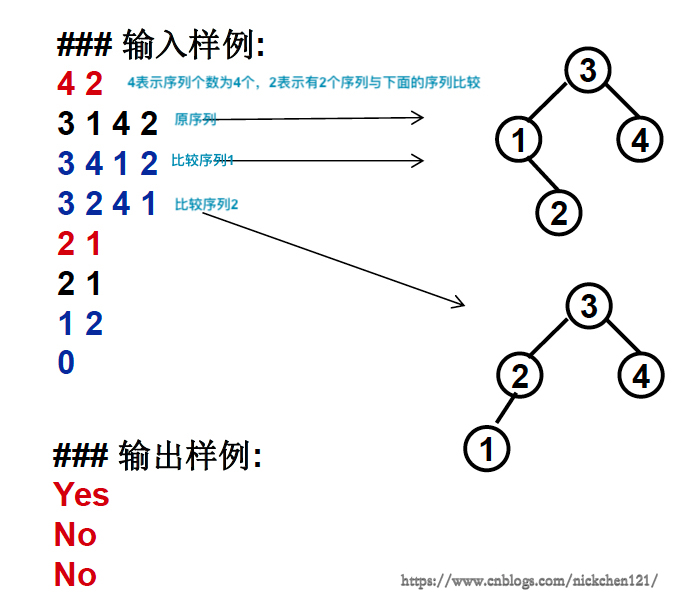
二、求解思路
两个序列是否对应相同搜索树的判别
- 分别建两颗搜索树的判别方法:根据两个序列分别建树,再判别树是否一样
- 不建树的判别方法

-
建一棵树,再判别其他序列是否与该树一致(本篇文章重点讨论)
- 搜索树表示
- 建搜索树T
- 判别一序列是否与搜索树T一致
三、搜索树表示
/* c语言实现 */
typedef struct TreeNode *Tree;
struct TreeNode
{
int v;
Tree Left, Right;
int flag;
}
程序框架搭建
/* c语言实现 */
int main()
{
对每组数据;
* 读入N和L;
* 根据第一行序列建树T;
* 依据树T分别判别后面的L个序列是否能与T形成同一搜索树并输出结果;
return 0;
}
int main()
{
int N, L, i;
Tree T;
scanf("%d", &N);
while (N) {
scanf("%d", &L);
T = MakeTree(N); // 读数据建搜索树T
for (i=0; i<L, i++){
if (Judge(T, N)) printf("Yes\n"); // 判别一序列是否与T构成一样的搜索树
else printf("No\n");
ResetT(T); // 清除T中的标记flag
}
FreeTree(T);
scanf("%d", &N);
}
return 0;
}
3.1 如何建搜索树
/* c语言实现 */
Tree MakeTree(int N)
{
Tree T;
int i, V;
scanf("%d", &V);
T = NewNode(V);
for (i=1; i<N; i++){
scanf("%d", &V);
T = Insert(T, V); // 按照搜索树顺序插入左右结点
}
return T;
}
Tree Insert(Tree T, int V)
{
if (!T) T = NewNode(V);
else{
if (V > T->v)
T->Right = Insert(T->Right, V);
else
T->Left = Insert(T->Left, V);
}
return T;
}
Tree NewNode(int V)
{
Tree T = (Tree)malloc(sizeof(struct TreeNode));
T->v = V;
T->Left = T->Right = NULL; // 左右子树设置为空
T->flag = 0;
return T;
}
3.2 如何判别
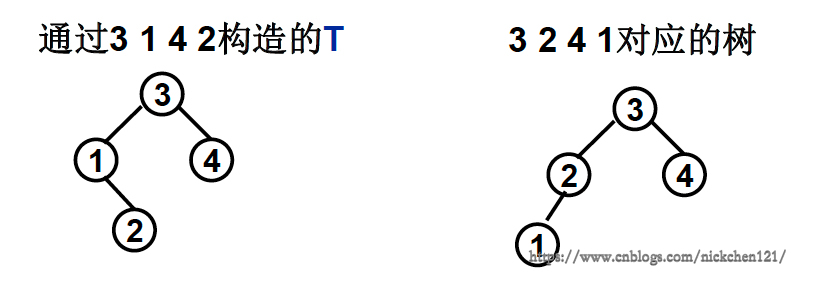
如何判别序列 3,2,4,1 是否与树T一致?
方法:在树T中按顺序搜索序列 3,2,4,1 中的每个数
- 如果每次搜索所经过的结点在前面均出现过,则一致
- 否则(某次搜索中遇到前面未出现的结点),则不一致
/* c语言实现 */
int check(Tree T, int V)
{
if (T->flag) {
// 如果flag为1,则递归搜索子结点
if (V < T->v) return check(T->Left, V);
else if (V > T->v) return check(T->Right, V);
}
else{
if (V == T->v){
T->flag = 1;
return 1;
}
else return 0;
}
}
// 有bug版本的Judge方法:当发现序列中的某个树与T不一致时,必须把序列后面的数都读完,如序列 3,2,4,1 ,在读取2时就会发现两颗是不相同的搜索树,下面这段代码则不会继续读取 4,1,而是把它归入下一个序列
int Judge(Tree T, int N)
{
int i, V;
scanf("%d", &V);
if (V != T->v) return 0;
else T->flag = 1;
for (i=1; i<N; i++){
scanf("%d", &V);
if (!check(T, V)) return 0;
}
return 1;
}
// 无bug版本的Judge方法
int Judge(Tree T, int N)
{
int i, V, flag = 0; // flag:0代表目前还一致,1代表已经不一致
scanf("%d", &V);
if (V != T->v) flag = 1;
else T->flag = 1;
for (i=1; i<N; i++){
scanf("%d", &V);
if ((!flag) && (!check(T,V))) flag = 1;
}
if (flag) return 0;
else return 1;
}
3.3 清空树
/* c语言实现 */
// 清除T中各结点的flag标记
void ResetT(Tree T)
{
if (T->Left) ResetT(T->Left);
if (T->Right) ResetT(T->Right);
T->flag = 0;
}
// 释放T的空间
void FreeTree(Tree T)
{
if (T->Left) FreeTree(T->Left);
if (T->Right) FreeTree(T->Right);
free(T);
}


