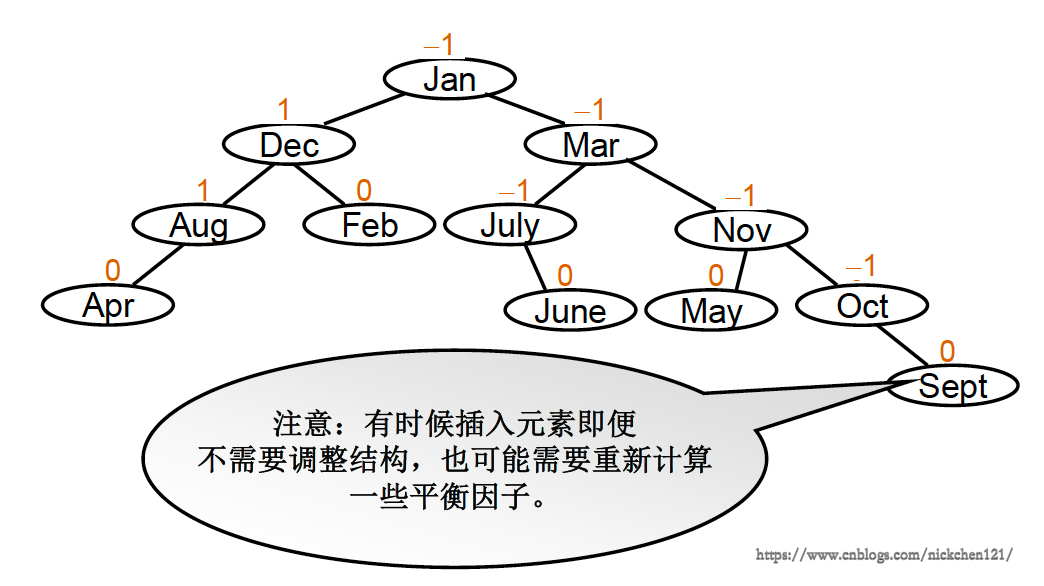
平衡二叉树
数据结构与算法_Python_C完整教程目录:https://www.cnblogs.com/nickchen121/p/11407287.html
更新、更全的《数据结构与算法》的更新网站,更有python、go、人工智能教学等着你:https://www.cnblogs.com/nickchen121/p/11407287.html
一、什么是平衡二叉树
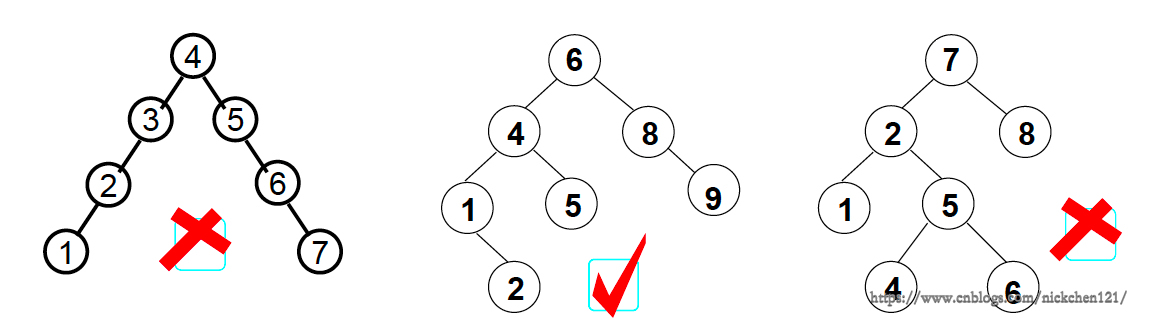
例:搜索树结点不同插入次序,将导致不同的深度和平均查找长度ASL
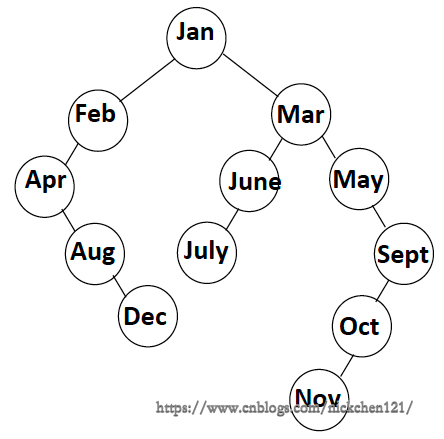
上图为按照自然月份序列构建的搜索树,它的ASL为\((1+2*2+3*3+4*3+5*2+6*1)/12=3.5\)
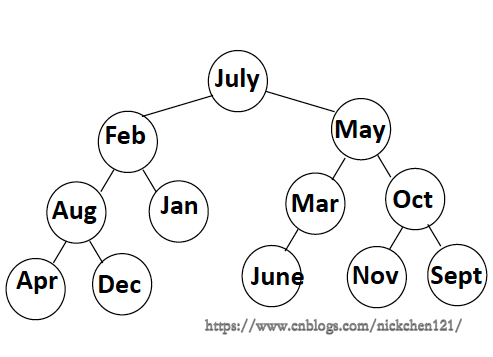
上图为按照平衡二叉树构建的搜索树,它的ASL为\(3.0\)
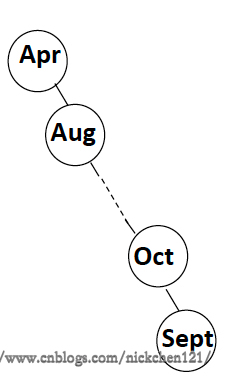
上图为按照月份字符串大小顺序构建的搜索树,他的ASL为\(6.5\)
“平衡因子”(Balance Factor,简称BF): \(BF(T) = h_L - h_R\),其中\(h_L\)和\(h_R\)分别为T的左、右子树的高度。
平衡二叉树(Balanced Binary Tree)(AVL树):空树,或者任一结点左、右子树高度差的绝对值不超过1,即\(BF(T)|\leq{1}\)
二、平衡二叉树的高度能达到\(log_2n\)吗?
如下图所示为完全二叉树的高度计算:
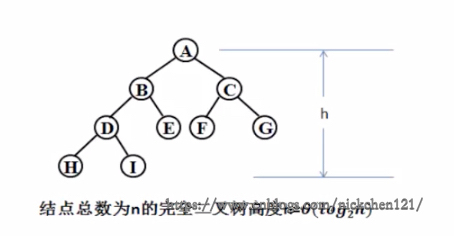
设\(n_h\)为高度为h的平衡二叉树的最少结点数。结点数最少时,我们可以得知左(右)子树最多比右(左)子树多一个结点:

上述公式类似于斐波那契序列: \(F_0=1,F_1=1,F_i=F_{i-1}+F_{i-2}\quad{f}or\quad{i}>1\),即我们可以通过斐波那契的规律,来探讨平衡二叉树的高度计算。
设\(n_h\)是高度为h的平衡二叉树的最小结点数,有如下推导:

按照上图的推导,我们可以得出:给定结点数为n的AVL树的最大高度为\(O(log_2n)\)
三、平衡二叉树的调整
3.1 右单旋

不平衡的“发现者”是Mar,“麻烦结点”Nov在发现者右子树的右边,因而叫做RR插入,需要RR旋转(右单旋)

3.2 左单旋
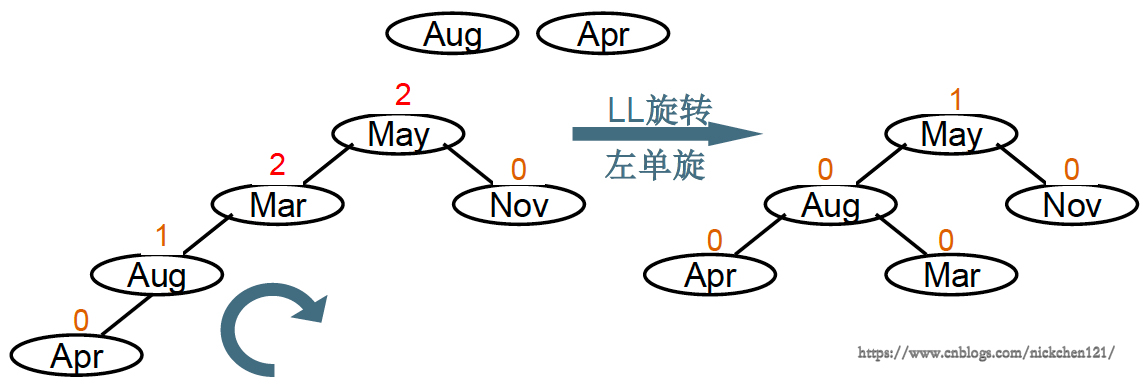
“发现者”是Mar,“麻烦结点”Apr在发现者左子树的左边,因而叫LL插入,需要LL旋转(左单旋)
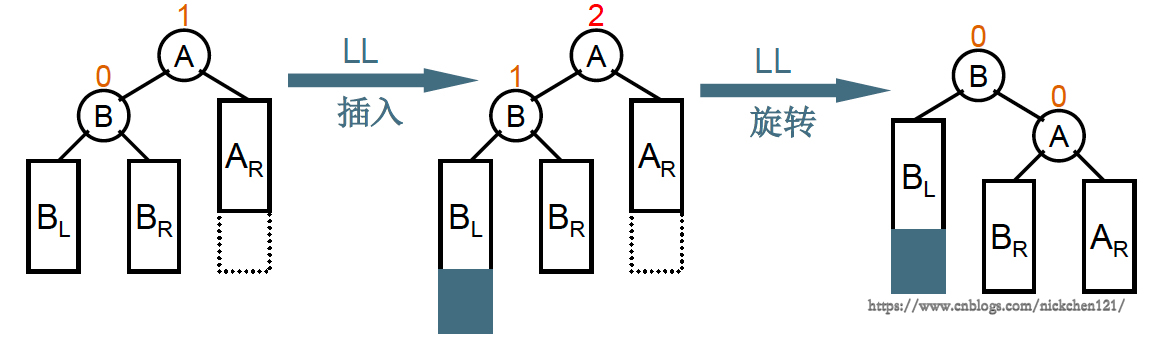
3.3 左-右双旋
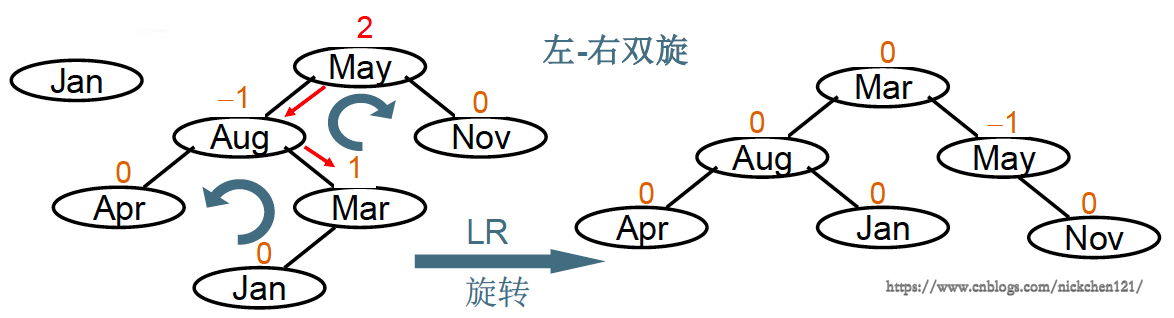
“发现者”是May,“麻烦结点”Jan在左子树的右边,因而叫LR插入,需要LR旋转
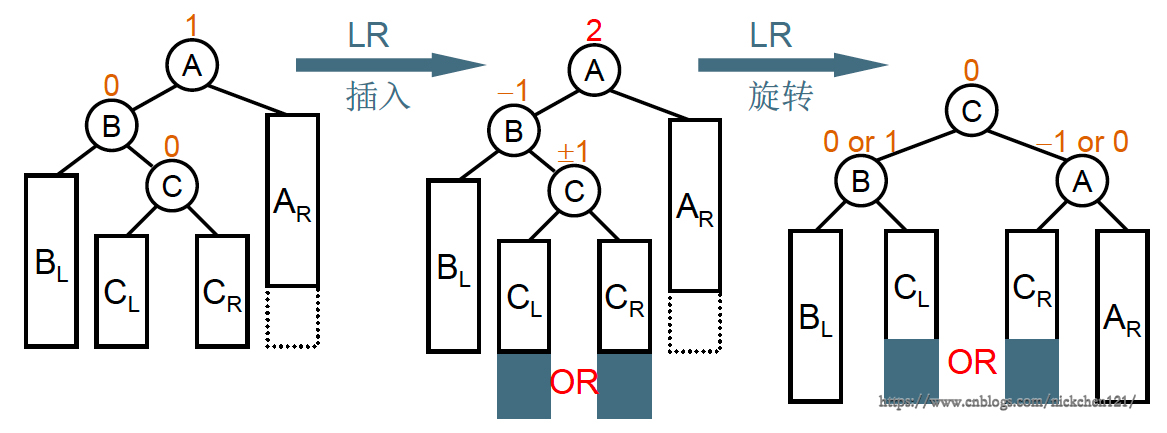
3.4 右-左双旋
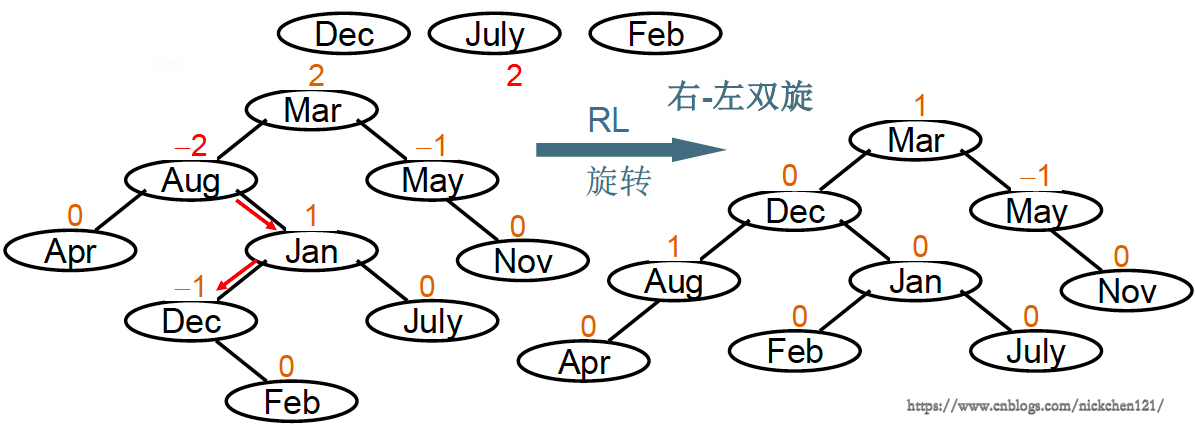
“发现者”是Aug,“麻烦结点”是Feb在右子树的左边,因而叫RL插入,需要LR旋转
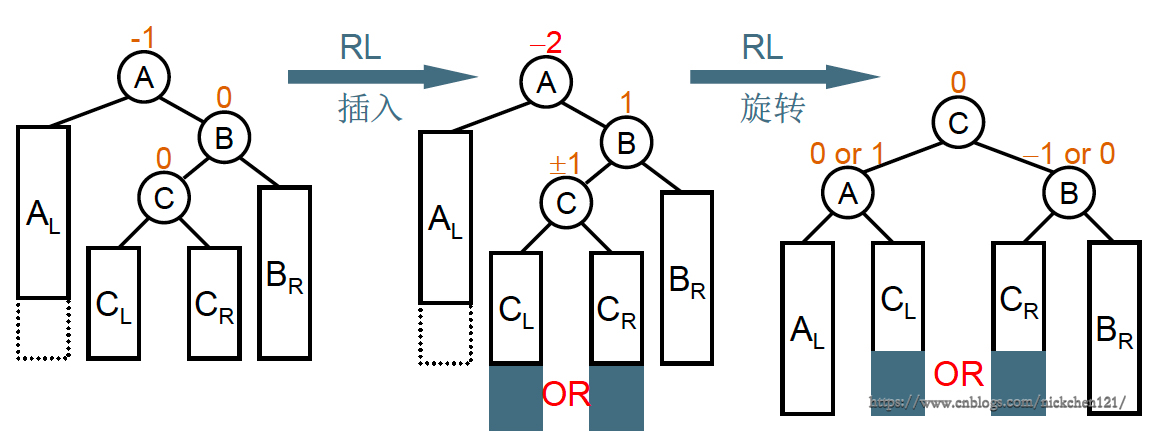
3.5 完善平衡二叉树
接下来我们使用上述所说的四种方法,完善我们的平衡二叉树。
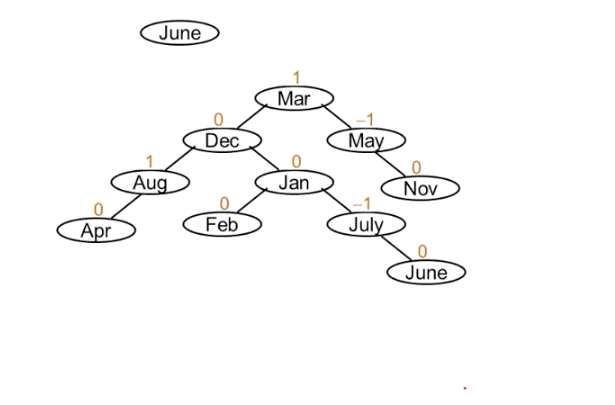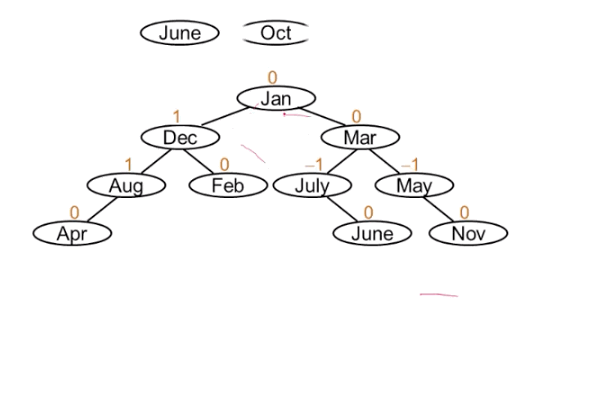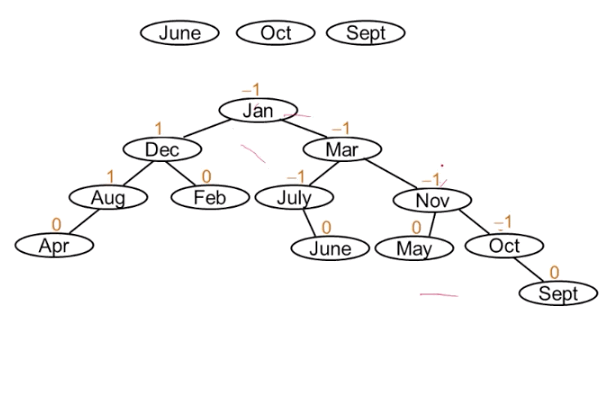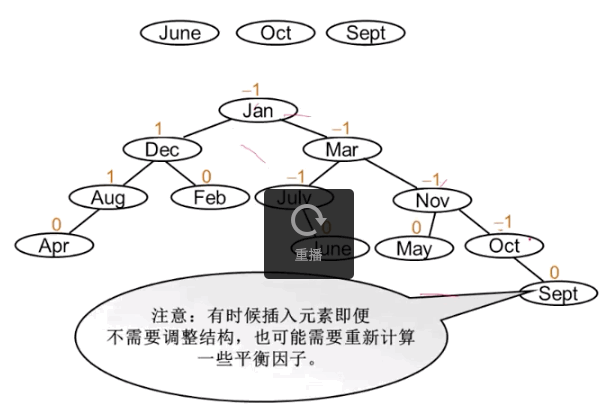
调整后的结果为: