线性表及其表示
数据结构与算法_Python_C完整教程目录:https://www.cnblogs.com/nickchen121/p/11407287.html
一、多项式的表示
1.1 一元多项式及其运算
一元多项式:\(f(x)=a_0+a_1x+\cdots+a_{n-1}x^{n-1}+a_nx^n\)
主要运算:多项式相加、相减、相乘等
如何用程序设计语言表示多项式,并且实现对多项式的操作?
1.2 如何表示多项式
- 多项式的关键数组
多项式项数\(n\)
各项系数\(a_i\) 及指数 \(i\)
1.3 方法1:顺序存储结构直接表示
数组各分量对应多项式各项:a[i]表示项\(x^i\)的系数\(a_i\)
例如:\(f(x)=4x^5-3x^2+1\)
表示如下图所示:

两个多现实相加:两个数组对应分量相加
问题:如何表示多项式\(x+3x^{2000}\),至少要有2001个分量表示,并且20001个分量中只有两项是非零的,这样的表示方法是有很大问题的
1.4 方法2:顺序存储结构表示非零项
每个非零项\(x_ix^i\)涉及两个信息:系数\(a_i\)和指数\(i\)
可以将一个多项式看成是一个\((a_i,i)\)二元组的集合。
用结构数组表示:数组分量是由系数\(a_i\)、指数\(i\)组成的结构,对应一个非零项
例如:\(P_1(x)=9x^{12}+15x^8+3x^2\)和\(P_2(x)=26x^{19}-4x^8-13x^6+82\)

按指数大小有序存储!
相加过程:从头开始,比较两个多项式当前对应项的指数
$ P1: (9,12), (15,8), (3,2) $
$ P2: (26,19), (-4,8), (-13,6), (82,0) $
$P3: (26,19) (9,12) (11,8) (-13,6) (3,2) (82,0) $
\(P_3(x)=26x^{19}+9x^{12}+11x^8-13x^6+3x^2+82\)
1.5 方法3:链表结构存储非零项
链表中每个结点存储多项式中的一个非零项,包括系数和指数两个数据域寄一个指针域

/* c语言实现 */
typedef struct PolyNode *Polynomial;
struct PolyNode{
int coef;
int expon;
Polynomial link;
}
# python语言实现
class PolyNode():
def __init__(coef, expon):
self.coef = coef
self.expon = expon
self.next = None
例如:
链表存储形式为:

链表形式表现的多项式加法过程类似于前两种方法。
二、什么是线性表
多项式表示问题的启示:
- 同一个问题可以有不同的表示(存储)方法
- 有一类共性问题:有序线性序列的组织和管理
“线性表(Linear List)”:由同类型数据元素构成有序序列的线性结构
- 表中元素个数称为线性表的长度
- 线性表没有元素时,称为空表
- 表起始位置称表头,表结束位置称表尾
三、线性表的抽象数据类型描述
类型名称:线性表(List)
数据对象集:线性表是\(n(\geq{0})\)个元素构成的有序序列\((a_1,a_2,\dots,a_n)\)
操作集:线性表\(L\in{List}\),整数\(i\)表示位置,元素\(X\in{ElementType\),线性表基本操作主要有:
List MakeEmpty():初始化一个空线性表\(L\);ElementType FindKth( int K, List L ):根据位序\(K\),返回相应元素 ;int Find( ElementType X, List L ):在线性表\(L\)中查找\(X\)的第一次出现位置;void Insert( ElementType X, int i, List L):在位序\(i\)前插入一个新元素\(X\);void Delete( int i, List L ):删除指定位序\(i\)的元素;int Length( List L ):返回线性表\(L\)的长度\(n\)。
四、线性表的顺序存储实现
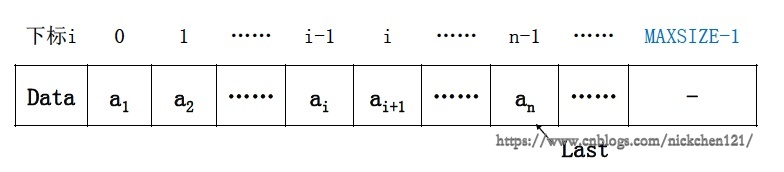
利用数组的连续存储空间顺序存放线性表的各元素
/* c语言实现 */
typedef struct LNode *List; /* 定义结构体指针 */
struct LNode{
ElementType Data[MAXSIZE]; /* 数组类型的Data,数组最大长度为MAXSIZE */
int Last;
}; /* 定义结构体 */
struct LNode L; /* 声明变量L */
List PtrL; /* 声明结构体PtrL */
访问下标为\(i\)的元素:L.Data[i]或PtrL->Data[i](取出PtrL所指向的结构体中包含的数据项Data[i])
线性表的长度:L.Last+1或PtrL->Last+1(取出PtrL所指向的结构体中包含的数据项Last并加1)
主要操作的实现
4.1 初始化(建立空的顺序表)
/* c语言实现 */
List MakeEmpty()
{
List PtrL;
PtrL = (List)malloc(sizeof(struct LNode)); /* 申请一个结构体 */
PtrL->Last = -1;
return PtrL;
}
4.2 查找
查找成功的平均比较次数为\((n+1)/2\),平均时间性能为\(O(n)\)
/* c语言实现 */
int Find(ElementType X, List Ptrl)
{
int i = 0;
while (i <= Ptrl->Last && Ptrl->Data[i] != X)
i++;
if (i > Ptrl->Last) return -1; /* 如果没找到,返回-1 */
else return i; /* 找到后返回的事存储位置 */
4.3 插入(第\(i(I\leq{I}\leq{n+1}\))个位置上插入一个值为\(X\)的新元素)
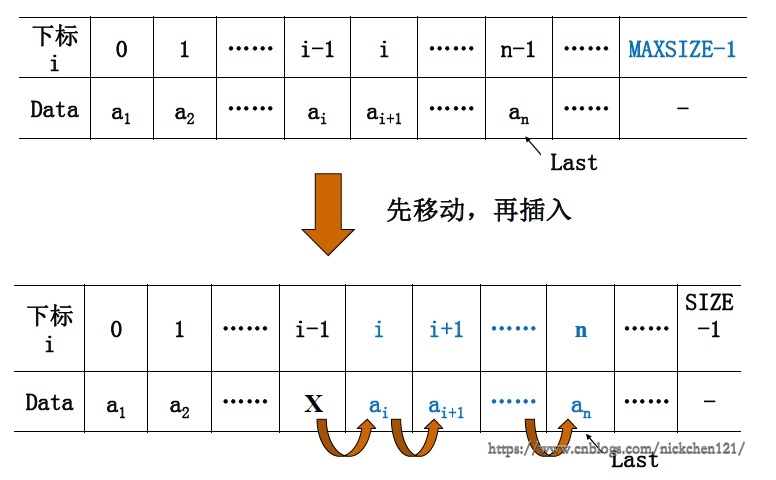
平均移动次数为\(n/2\),平均时间性能为\(O(n)\)
/* c语言实现 */
void Insert(ElementType X, int i, List PtrL)
{
int j;
if (Ptrl->Last == MAXSIZE - 1){ /* 表空间已满,不能插入 */
printf("表满");
return ;
}
if (i<1 || PtrL->Last+2){
printf("位置不合法");
return ;
}
for (j=PtrL->Last; j>=i-1; j--)
PtrL->Data[j+1] = Ptrl->Data[j]; /*将a_i~a_n倒序向后移动*/
PtrL->Data[i-1] = X; /* 新元素插入 */
PtrL->Last++; /* Last仍指向最后元素 */
return;
}
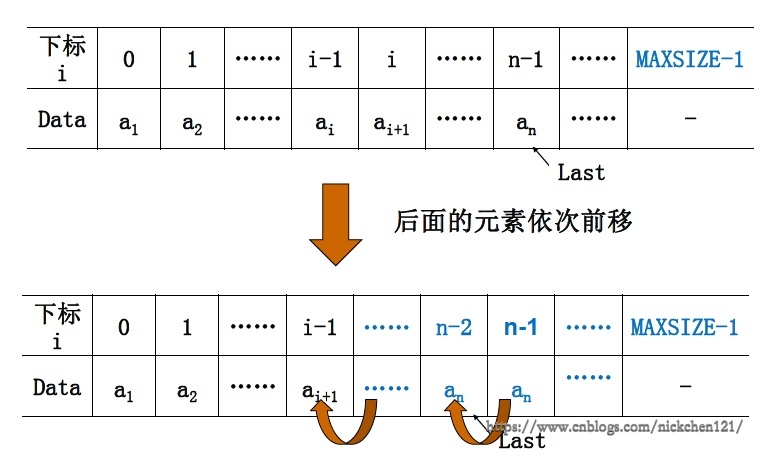
4.4 删除(删除表的第\(i(1\leq{i}\leq{n})\)个位置上的元素)
平均移动次数为\((n-1)/2\),平均时间性能为\(O(n)\)
/* c语言实现 */
void Delete(int i, List Ptrl)
{
int j;
if(i<1 || i>PtrL->Last+1){ /* 检查空表及删除位置的合法性 */
printf("不存在第%d个元素", i);
return ;
}
for (j=i, j<=Ptrl->Last; j++)
PtrL->Data[j-1] = Ptrl->Data[j]; /* 将a_{i+1}~a_n顺序向前移动*/
Ptrl->Last--; /* Last仍指向最后元素 */
return;
}
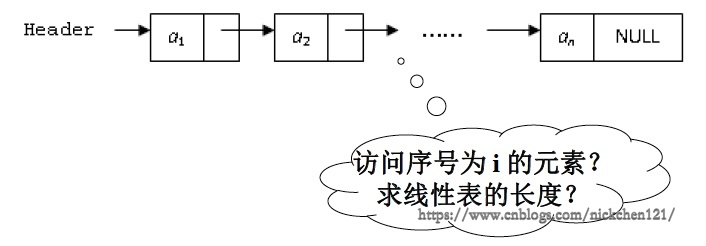
五、线性表的链式存储实现
不要求逻辑上相邻的两个元素物理上也相邻;通过“链”建立起数据元素之间的逻辑关系。即插入、删除不需要移动数据元素,只需要修改“链”。
/* c语言实现 */
typedef struct LNode *List;
struct LNode{
ElementType Data;
List Next;
};
struct Londe L;
List PtrL;
5.1 求表长
时间性能为\(O(n)\)
/* c语言实现 */
int Length(List PtrL)
{
List p = PtrL; /* p指向表的第一个结点 */
int j = 0;
while (p) {
p = p->Next;
j++; /* 当前p指向的是第j个结点 */
}
return j;
}
5.2 查找:
平均时间性能为\(O(n)\)
5.2.1 按序号查找:FindKth;
/* c语言实现 */
List FindKth(int K, List PtrL)
{
List p = Ptrl;
int i = 1;
while (p != NULL && i < K){
p = p->Next;
i++;
}
if (i==K) return P; /* 找到第K个,返回指针 */
else return NULL; /* 否则返回空 */
5.2.2 按值查找:Find
/* c语言实现 */
List Find(ElementType X, List PtrL)
{
List p = PtrL;
while (p != NULL && p->Data != X)
p = p->Next;
return p;
}
-
插入(在第\(i-1(1\leq{i}\leq{n+1})\)个结点后插入一个值为\(X\)的新结点)
- 先构造一个新结点,用s指向;
- 再找到链表的第\(i-1\)个j结点,用\(p\)指向;
- 然后修改指针,插入结点(\(p\)之后插入新结点是\(s\))

/* c语言实现 */
List Insert(ElementType X, int i, List PtrL)
{
List p, s;
if (i == 1){ /* 新结点插入在表头 */
s = (List)malloc(sizeof(struct LNode)); /* 申请、填装结点 */
s->Data = X;
s->Next = Ptrl;
return s; /* 返回新表头指针 */
}
p = FindKth(i-1, Ptrl); /* 查找第i-1个结点 */
if (p == NULL){ /* 第i-1个不存在,不能插入 */
printf("参数i错");
return NULL;
}else{
s = (List)malloc(sizeof(struct LNode)); /* 申请、填装结点 */
s->Data = X;
s->Next = p->Next; /* 新结点插入在第i-1个结点的后面*/
p->Next = s;
return PtrL;
}
5.3 删除(删除链表的第\(i(1\leq{i}\leq{n})\)个位置上的结点)
平均查找次数为\(n/2\),平均时间性能为\(O(n)\)
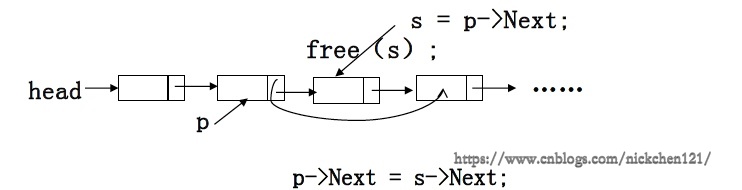
- 先找到链表的第\(i-1\)个结点,用\(p\)指向
- 再用指针\(s\)指向要被删除的结点(\(p\)的下一个结点);
- 然后修改指针,删除\(s\)所指结点;
- 最后释放\(s\)所指结点的空间。
/* c语言实现 */
List Delete(int i, List PtrL)
{
List p, s; /* 若要删除的事表的第一个结点 */
if (i == 1){
s = PtrL; /* s指向第1个结点 */
if (PtrL != NULL) PtrL = PtrL->Next; /* 从链表中删除 */
else return NULL;
free(s); /* 释放被删除结点 */
return PtrL;
}
p = FindKth(i-1, PtrL); /* 查找第i-1个结点 */
if (p == NULL){
printf("第%d个结点不存在", i-1); return NULL;
} else if (i->Next == NUll){
printf("第%d个结点不存在", i); return NULL;
} else {
s = p->Next; /* s指向第i个结点 */
p->Next = s->Next; /* 从链表中删除*/
free(s); /* 释放被删除结点*/
return PtrL;
}
六、二元多项式的表示
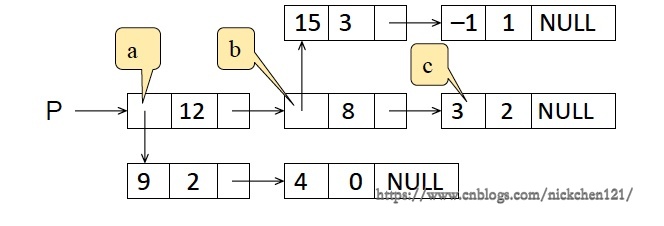
我们知道了一元多项式的表示,那么二元多项式又该如何表示?比如,给定二元多项式:\(P(x,y)=9x^{12}y^2+4x^{12}+15x^8y^3-x^8y+3x^2\)
可以将上述二元多项式看成关于\(x\)的一元多项式:\(P(x,y)=(9y^2+4)x^{12}+(15y^3-y)x^8+3x^2\quad(ax^{12}+bx^8+cx^2)\)
因此,上述二元多项式可以用“复杂”链表表示为下图所示:
七、广义表
- 广义表是线性表的推广
- 对于线性表而言,\(n\)个元素都是基本的单元素;
- 广义表中,这些元素不仅可以是单元素也可以是另一个广义表。
/* c语言实现 */
typedef struct GNode *GList;
struct GNode{
int Tag; /* 标志域:0表示结点是单元素,1表示结点是广义表 */
union{ /* 字表指针域Sublist与单元素数据域Data复用,即公用存储空间 */
ElementType Data;
Glist SubList;
}URegion;
Glist Next; /* 指向后继结点 */
}

八、多重链表
多重链表:链表中的结点可能同时隶属于多个链
- 多重链表中结点的指针域会有多个,如前面例子包含了\(Next\)和\(SubList\)两个指针域;
- 但包含两个指针域的链表并不一定是多重链表,比如在双线链表不是多重链表。
多重链表有广泛的用途:基本上如树、图这样相对复杂的数据结构都可以采用多重链表方式实现存储。
8.1 例1:多重链表表示矩阵
矩阵可以用二维数组表示,但二维数组表示有两个缺陷:
- 一是数组的大小需要事先确定,
- 对于“稀疏矩阵”,将造成大量的存储空间浪费。
分析:采用一种典型的多重链表——十字链表来存储稀疏矩阵
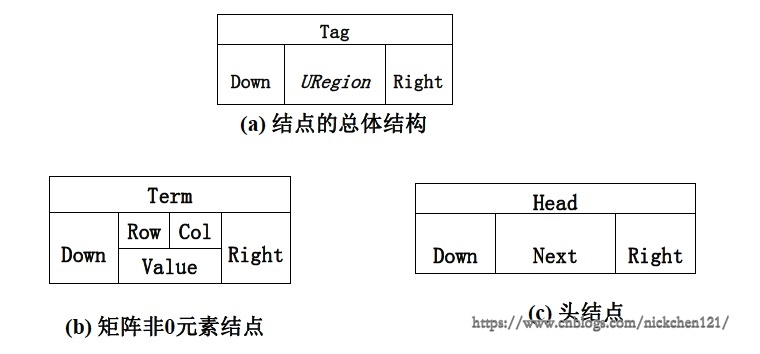
- 只存储矩阵非0元素相:结点的数据域:行坐标\(Row\)、列坐标\(Col\)、数值\(Value\)
- 每个结点通过两个指针域,把同行、同列串起来;
行指针(或称为向右指针)Right
列指针(或称为向下指针)Down
下图为矩阵A的多重链表图:
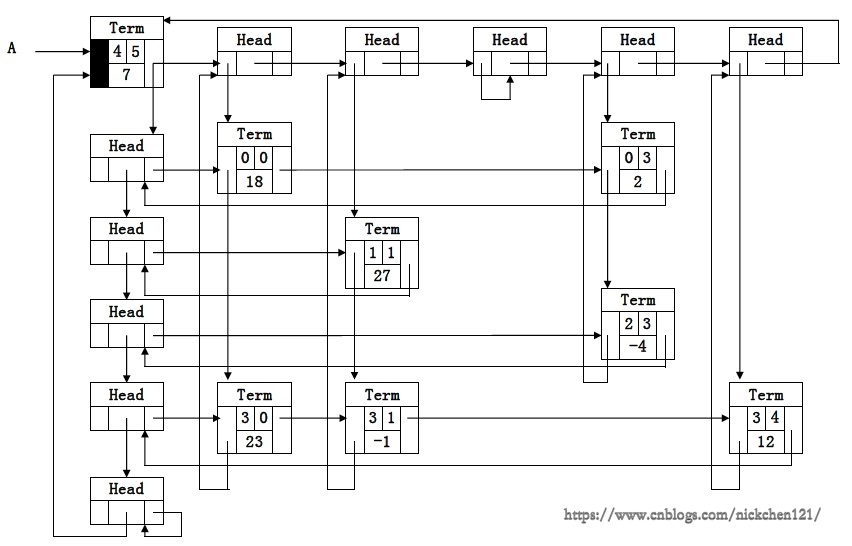
用一个标识域\(Tag\)来区分头结点和非0元素结点;
头结点的标识值为“Head”,矩阵非0元素结点的标识值为“Term”。
九、Python实现-单链表
class Node(object):
def __init__(self, val, p=0):
self.data = val
self.next = p
class LinkList(object):
def __init__(self):
self.head = 0
def __getitem__(self, key):
if self.is_empty():
print('linklist is empty.')
return
elif key < 0 or key > self.getlength():
print('the given key is error')
return
else:
return self.getitem(key)
def __setitem__(self, key, value):
if self.is_empty():
print('linklist is empty.')
return
elif key < 0 or key > self.getlength():
print('the given key is error')
return
else:
self.delete(key)
return self.insert(key)
def initlist(self, data):
self.head = Node(data[0])
p = self.head
for i in data[1:]:
node = Node(i)
p.next = node
p = p.next
def getlength(self):
p = self.head
length = 0
while p != 0:
length += 1
p = p.next
return length
def is_empty(self):
if self.getlength() == 0:
return True
else:
return False
def clear(self):
self.head = 0
def append(self, item):
q = Node(item)
if self.head == 0:
self.head = q
else:
p = self.head
while p.next != 0:
p = p.next
p.next = q
def getitem(self, index):
if self.is_empty():
print('Linklist is empty.')
return
j = 0
p = self.head
while p.next != 0 and j < index:
p = p.next
j += 1
if j == index:
return p.data
else:
print('target is not exist!')
def insert(self, index, item):
if self.is_empty() or index < 0 or index > self.getlength():
print('Linklist is empty.')
return
if index == 0:
q = Node(item, self.head)
self.head = q
p = self.head
post = self.head
j = 0
while p.next != 0 and j < index:
post = p
p = p.next
j += 1
if index == j:
q = Node(item, p)
post.next = q
q.next = p
def delete(self, index):
if self.is_empty() or index < 0 or index > self.getlength():
print('Linklist is empty.')
return
if index == 0:
q = Node('', self.head)
self.head = q
p = self.head
post = self.head
j = 0
while p.next != 0 and j < index:
post = p
p = p.next
j += 1
if index == j:
post.next = p.next
def index(self, value):
if self.is_empty():
print('Linklist is empty.')
return
p = self.head
i = 0
while p.next != 0 and not p.data == value:
p = p.next
i += 1
if p.data == value:
return i
else:
return -1
l = LinkList()
l.initlist([1, 2, 3, 4, 5])
print(l.getitem(4)) # 5
l.append(6)
print(l.getitem(5)) # 6
l.insert(4, 40)
print(l.getitem(3)) # 4
print(l.getitem(4)) # 40
print(l.getitem(5)) # 5
l.delete(5)
print(l.getitem(5)) # 6
l.index(5)

