应用实例-最大子列和问题

目录

数据结构与算法_Python_C完整教程目录：https://www.cnblogs.com/nickchen121/p/11407287.html

一、最大子列和问题

给定\(N\)个整数的序列\({A_1,A_2,\dots,A_N}\)，求函数\(f(i,j)=max\{0,\sum_{k=I}^jA_K\}\)的最大值。

序列中有多个子列，我们需要从中找出子列和最大的子列。

1.1 算法1-暴力破解

/* c语言实现 */

int MaxSubseqSum1(int A[], int N)
{ int ThisSum, MaxSum = 0;
  int i, j, j;
  for(i=0; i<N; i++){  /* i是子列左端位置 */
    for (j=i; j<N; j++){  /* i是子列右端位置 */
      ThisSum = 0; /* ThisSum是从A[i]到A[j]的子列和 */
      for(k=i; k<=j; k++)
        ThisSum += A[k];
      if(ThisSum > MaxSum)  /* 如果刚得到的这个子列和更大 */
        MaxSum = ThisSum;  /* 则更新结果 */
   }  /* j循环结束 */
 }  /* i循环结束 */
 return MaxSum;
}

# python语言实现

def max_subseq_sum1(arr: list, n: int):
  max_sum = 0
  for i in range(n):
    for j in range(i, n):
      this_sum = 0
      for k in range(i, j):
        this_sum += arr[k]
      if this_sum > max_sum:
        max_sum = this_sum

时间复杂度：

\[T(n) = O(N^3) \]

当我们知道\(i-j\)的和之后，没必要从头开始加，对于k的循环是多余的。

1.2 算法2-适当优化

/* c语言实现 */

int MaxSubseqSum2(int A[], int N)
{ int ThisSum, MaxSum = 0;
  int i, j, j;
  for(i=0; i<N; i++){  /* i是子列左端位置 */
    ThisSum = 0; /* ThisSum是从A[i]到A[j]的子列和 */
    for (j=i; j<N; j++){  /* i是子列右端位置 */
      ThisSum += A[k];
      /* 对于相同的i，不同的j，只要在j-1次循环的基础上累加1项即可 */
      if(ThisSum > MaxSum)  /* 如果刚得到的这个子列和更大 */
        MaxSum = ThisSum;  /* 则更新结果 */
   }  /* j循环结束 */
 }  /* i循环结束 */
 return MaxSum;
}

# python语言实现

def max_subseq_sum2(arr: list, n: int):
  max_sum = 0
  for i in range(n):
    this_sum = 0
    for j in range(i, n):
      this_sum += arr[k]
      if this_sum > max_sum:
        max_sum = this_sum

时间复杂度：

\[T(n) = O(N^2) \]

一个专业的程序猿，设计了一个\(O(N^2)\)的算法，应该本能的想到是否能把他改进为\(O(Nlog_N)\)的算法。

1.3 算法3-分而治之

先把数组从中间一分为二，递归的解决左半部分的问题，得到左边的最大子列和；递归的解决右半部分的问题，得到右边的最大子列和；解决跨越中间的最大子列和，从三者中取出最大的子列和，即为解。

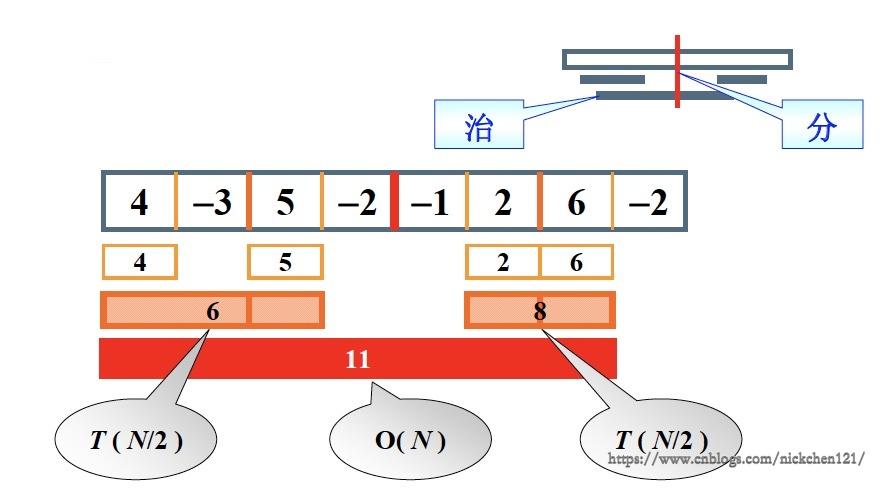
时间复杂度：

\[\begin{align} T(n) & = 2T(N/2)+cN,\,\quad{T}(1)=O(1) \\ & = \text{注意$T(n)$和$T(N/2)$的转换关系}\\ & = 2[2T(N/2^2)+cN/2]+cN \\ & = 2^kO(1)+ckN\quad\text{其中$N/2^k=1$，即$k=log_2N$} \\ & = O(NlogN) \end{align} \]

1.4 算法4-在线处理

由于连续子列和出现负数，往后加数字只会让后面的数字越来越大，因此可以提前让子列和归零。

“在线”的意思是指每输入一个数据就进行即时处理，在任何一个地方中止输入，算法都能正确给出当前的解。

/* c语言实现 */

int MaxSubseqSum4(int A[], int N)
{ int ThisSum, MaxSum;
  int i;
  ThisSum = MaxSum = 0;
  for(i=0; i<N; i++){
    ThisSum += A[i]; /* 向右累加 */
    if(ThisSum > MaxSum)
      MaxSum = ThisSUm; /* 发现更大和则更新当前结果 */
    else if(ThisSum < 0) /* 如果当前子列和为负 */
      ThisSum = 0; /* 则不可能使后面的部分和增大，抛弃之 */
 }
 return MaxSum;
}

# python语言实现

def max_subseq_sum4(arr: list, n: int):
  this_sum = max_sum = 0
  for i in range(n):
    this_sum += arr[i]
    if this_sum > max_sum:
      max_sum = this_sum
    elif this_sum < 0:
      this_sum = 0

时间复杂度：

\[T(N) = O(N) \]

由于时间复杂度较快，所以对于其他人理解是很困难的。

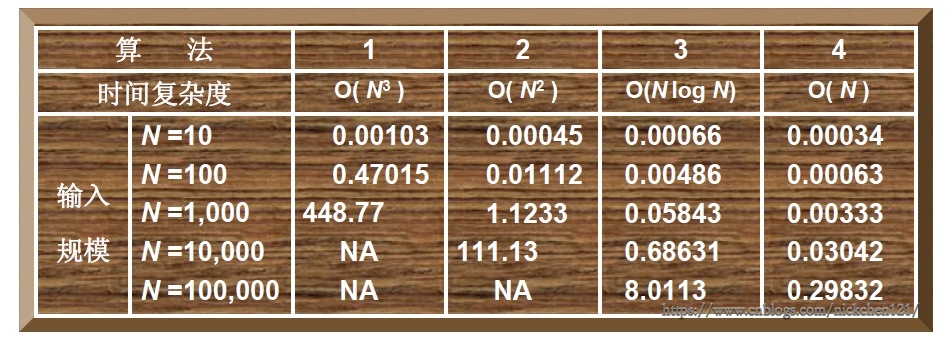
二、算法运行时间比较

posted @ 2019-08-25 18:25  B站-水论文的程序猿  阅读(1175)  评论(0)  编辑  收藏  举报