01-凸集
01-凸集
凸优化从入门到放弃完整教程地址:https://www.cnblogs.com/nickchen121/p/14900036.html
一、仿射和凸集
[直线和线段] 令 \(x_1\ne x_2\) 是 \(R^n\) 中的两点, \(y=\theta x_1+(1-\theta)x_2\) , \(\theta\in R\) 表达了过点 \(x_1,x_2\) 的一条直线,当 \(\theta\) 取 \(0,1\) 之间的数时,点 \(y\) 从 \(x_2\) 移动到 \(x_1\) ,对应着 \(x_1,x_2\) 之间的线段。
- 另一种表达式: \(y=x_2+\theta(x_1+x_2)\) 给出另一种解释—— \(y\) 是从基点 \(x_2\) 出发,沿方向 \((x_1-x_2)\) 延申 \(\theta\) 倍处的点。
- 注:直线和线段的判断其实就是参考 \(\theta\) 的取值,也就是看通过\(\theta\)形成的点 \(y\) 是在\(x_1\) 和 \(x_2\) 连线的内部还是外部。
[仿射集 Affine sets] 一个集合 \(C\subseteq R^n\) 是仿射的,如果C中任意两不同点之间点的直线都在 \(C\) 中。也就是 \(\forall x_1,x_2\in C, \theta\in R\) ,有 \(\theta x_1+(1-\theta)x_2\in C\) .
- \(C\) 中包含了 \(C\) 中任意两点的线性组合。
[仿射组合 Affine combination] 我们称形如 \(\theta_1x_1+....+\theta_k x_k\) , \((\theta_1+...+\theta_k=1)\) 的点为点 \(x_1,...,x_k\) 的仿射组合。
- 一个仿射集包含其所有点的所有仿射组合。
- 注:仿射组合,其实就可以看成是二维空间内的一条条直线,也就是点与点的线性组合
[仿射集的子空间] 如果 \(C\) 是一个仿射集, \(x_0\in C\) 那么集合 \(V=C-x_0=\{x-x_0| x\in C\}\) 是一个子空间,也就是对加法和标量乘法封闭。
证明:假设 \(v_1,v_2\in V\) 和 \(\alpha,\beta\in R\) , 我们有 \(v_1+x_0\in C\) , \(v_2+x_0\in C\) . 并且 \(av_1+\beta v_2+x_0= \alpha(v_1+x_0)+\beta(v_2+x_0)+(1-\alpha-\beta)x_0\in C\) , 所以 \(\alpha v_1+\beta v_2 \in V\) .
因此仿射集 \(C\) 可以写成: \(C=V+x_0=\{v+x_0|v\in V\}\) . 也就是一个子空间加上一个平移 (offset)。
注:子空间,可以想象成我随便找一个定点 \(x_0\),然后空间内的任意点与定点的连线形成一个新的空间,这个空间就是一个子空间。
[仿射集的维数] 我们定义仿射集 \(C\) 的维数为其子空间 \(V=C-x_0\) 的维数, \(x_0\) 可以是 \(C\) 中的任意元素。
[仿射包 Affine hull] 一个集合 \(C\subseteq R^n\) 中所有点的所有仿射组合的集合叫做C的仿射包,记作 \(aff\,C\) :
\(aff\,C=\{\theta_1x_1+...+\theta_kx_k| x_1,...,x_k\in C, \theta_1+...+\theta_k=1\}.\)
- 仿射包是包含 \(C\) 的最小仿射集: 如果 \(S\) 是任意带有 \(C\in R^n\) 的仿射集,那么 \(aff\,C\subseteq S\) .
- 注:仿射包其实就是仿射集合的无限延伸,下面讲到凸包的时候容易理解“包”的概念
[仿射维度] 定义集合 \(C\) 的仿射维度为它的仿射包的维度。
例如 \(R^2\) 内的单位元 \(\{x\in R^2| x_1^2+x_2^2=1\}\) ,它的仿射包是整个 \(R^2\) ,所以仿射维度是2维。
[相对内部 relative interior] 如果一个集合 \(C\subseteq R^n\) 的仿射维度小于 \(n\) ,那么这个集合在仿射集里 \(aff\,C\ne R^n\) ,我们将集合C的相对内部定义为 \(relint\, C = \{x\in C | B(x,r)\cap aff\,C \subseteq C, \; for\, some\; r>0 \}\)
其中 \(B(x,r)=\{y| ||y-x||\leq r\}\) 是以 \(x\) 为中心, \(r\) 为半径的球。
注:相对内部其实就是自己在集合内部定义一个范围出来
[相对边界 relative boundary] 集合 \(C\) 的相对边界定义为 \(cl\,C \backslash relint\,C\) , \(cl\,C\) 是 \(C\) 的闭包。
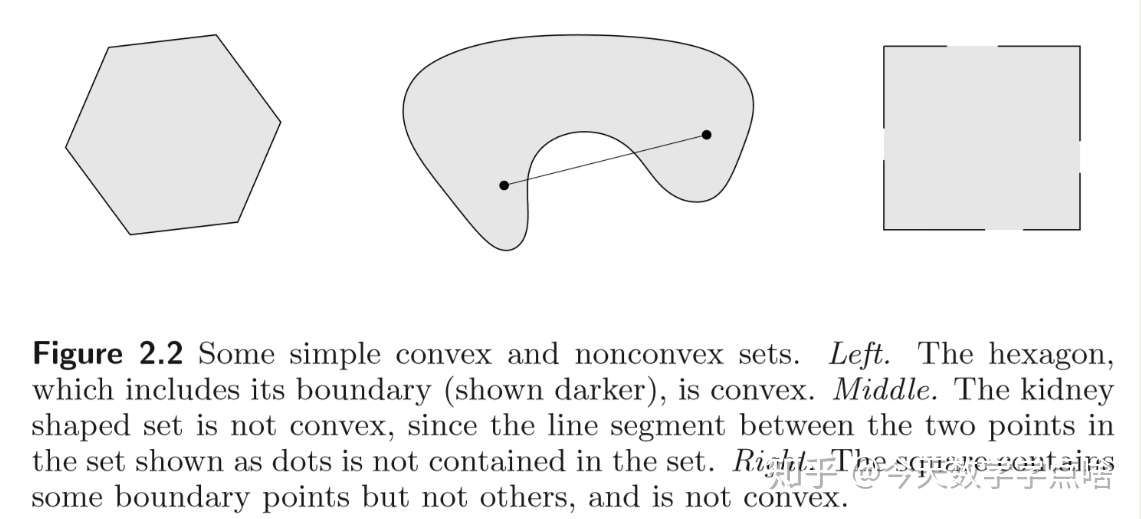
[凸集 convex set] 一个集合 \(C\) 是凸的,如果 \(C\) 中任意两点之间的线段都在 \(C\) 中。也就是 \(\forall x_1,x_2\in C\) , \(\forall \theta \in [0,1]\) 有 \(\theta x_1+(1-\theta)x_2\in C.\)
注:仿射集和凸集的主要区别,可以这样去想,仿射集是可以无限延伸的,而凸集一般都是有限定范围的。就类似于直线和线段的理解。
和仿射的区别:仿射中 \(\theta\in R\) 。
[凸组合] 形如 \(\theta_1x_1+...+\theta_k x_k, \theta_1+...+\theta_k=1,\theta_i\geq0,i=1,...,k\) 的点称为点 \(x_1,...,x_k\) 的凸组合。
点的凸组合,可以看作是这些点的加权平均。
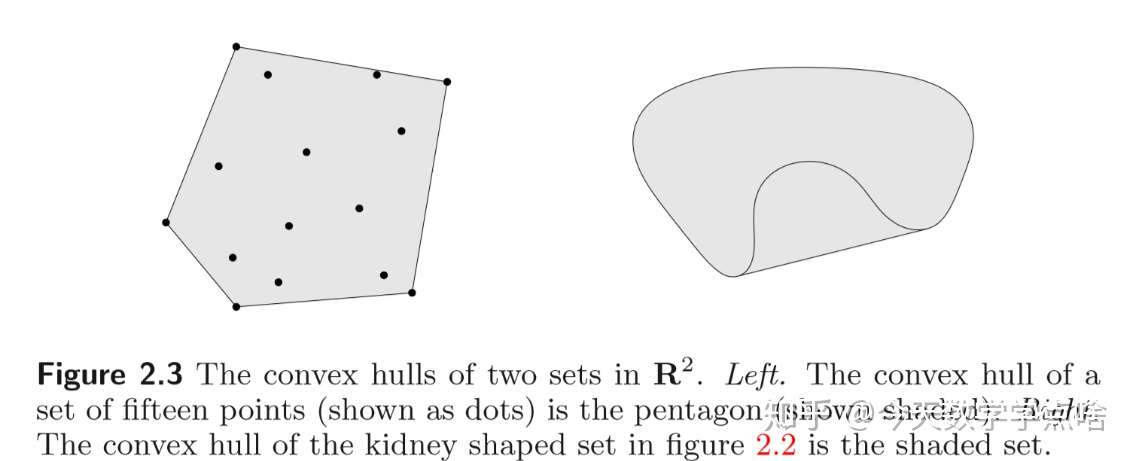
[凸包 convex hull] 集合 \(C\) 的凸包,是 \(C\) 中所有点的所有凸组合的集合,记作 \(convC\) 。 \(convC=\{\theta_1x_1+...+\theta_kx_k | x_i\in C, \theta_i\geq 0, i=1,...,k, \theta_1+...+\theta_k=1\}.\)
注:从凸包理解仿射包,其实就是对非凸集合做一个延伸扩展,让其可凸
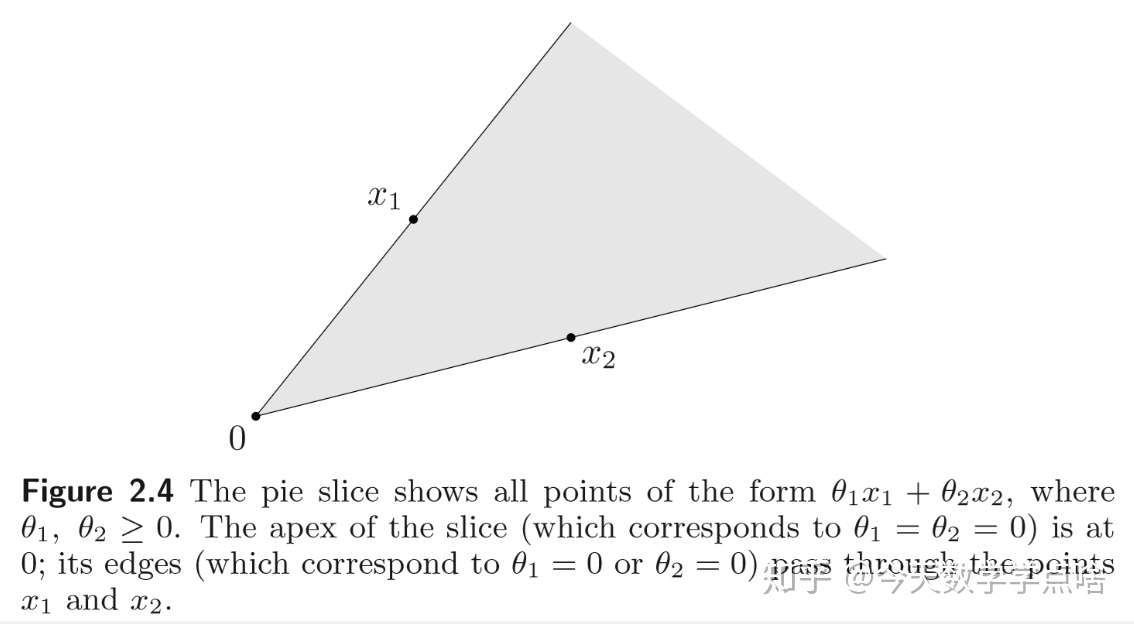
[锥 cone,凸锥] 一个集合 \(C\) 被称为一个锥或者 nonnegative homogeneous 如果对于每个点 \(x\in C\) 和 \(\theta \geq 0\) 都有 \(\theta x\in C\) 。
一个集合 \(C\) 被称为凸锥,如果它是凸集且是一个锥。也就是对于任意的 \(x_1,x_2\in C\) 和 \(\theta_1,\theta_2\geq 0\) 我们有 \(\theta_1x_1+\theta_2x_2\in C\) . 如图,就像一块披萨:
注:锥很好理解的,其实就可以看成射线的延伸。凸锥其实就是从原点开始两条射线的延伸的形成的范围
[锥组合] 一个形如 \(\theta_1x_1+...+\theta_kx_k, \theta1,...,\theta_k\geq 0\) 的点叫做点 \(x_1,...,x_k\) 的锥组合(或非负线性组合)。
- 如果点 \(x_i\) 在凸锥 \(C\) 中,那么 \(x_i\) 的每个锥组合都在 \(C\) 中。
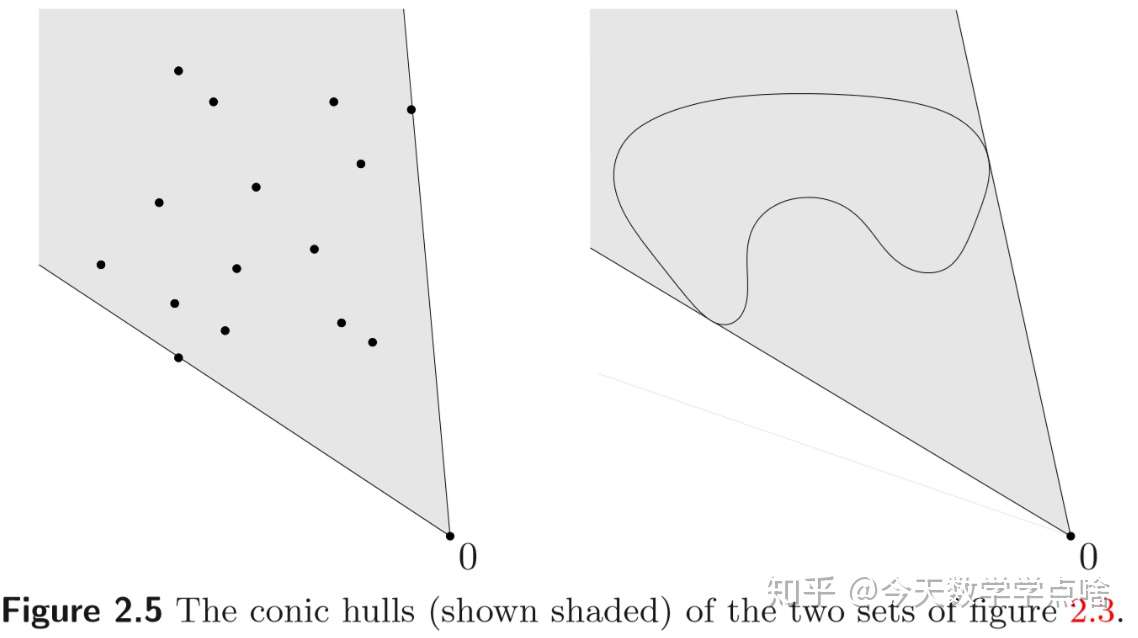
[锥包 conic hull] 一个集合 \(C\) 的锥包是 \(C\) 中所有点的所有锥组合的集合。也就是 \(\{\theta_1x_1+...+\theta_kx_k | x_i\in C, \theta_i\geq 0 , i=1,...,k\}\) .
- 锥包是包含 \(C\) 的最小的锥。
二、一些重要的例子
[简单的例子]
- 空集和任何单一的点 \(\{x_0\}\) 和整个空间 \(R^n\) 是 \(R^n\) 的仿射子集(凸)。
- 任意直线都是仿射的,如果它过零点,那么它是一个子空间,于是也是一个凸锥。
- 一个线段是凸的,但是不是仿射的(除非退化成一个点)。
- 一个射线(ray)形如 \(\{x_0+\theta v| \theta\geq 0\}\) , \(v\ne 0\) 是凸的,但是不是仿射的。如果基点 \(x_0\) 是 \(0\) 的话,它就是一个凸锥。
- 任何子空间都是仿射的,也是一个凸锥。
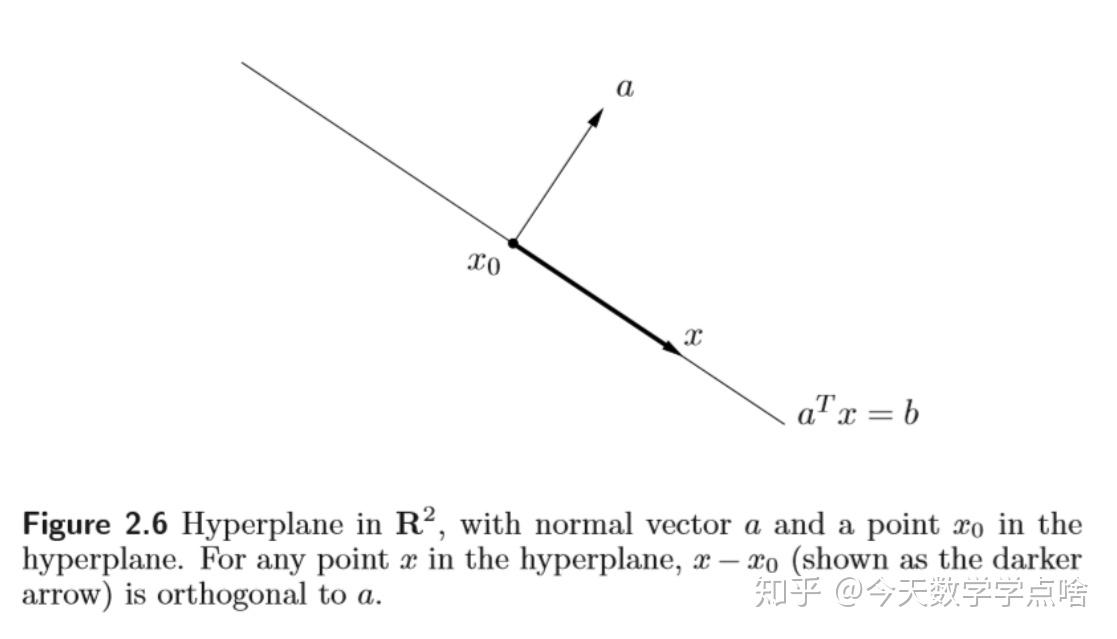
[超平面 Hyperplane] 一个超平面是集合 \(\{x|a^Tx=b\}\) ,,其中 \(a\in R^n\) , \(a\ne0\) , \(b\in R\) .
- 从分析的角度说,它是一个线性方程的解集(是仿射的)。
- 从几何的角度说,是和向量 \(a\) 有相等的内积的点的集合。注:或者说一个法向量为 \(a\) 的超平面,而 \(b\) 就是超平面离原点的平移。可以写成 \(\{x| a^T(x-x_0)=0\}\) , \(x_0\) 是平面上任意一点。
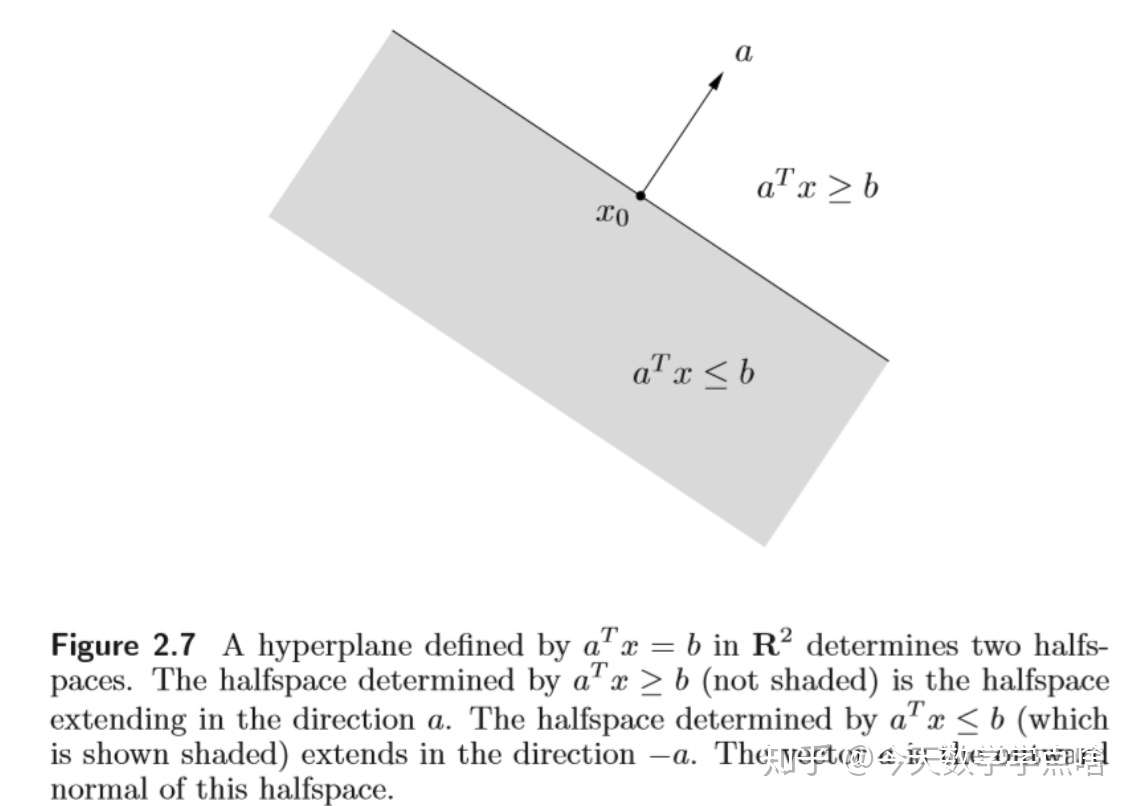
[半空间 Halfspace] 一个(闭的)半空间是一个集合 \(\{x| a^Tx\leq b\}\) 其中 \(a\ne 0\) .
- 它是一个线性不等式的解集。
- 它是凸的,但是不是仿射的。
- 几何解释:半空间可以写成: \(\{x| a^T(x-x_0)\leq 0\}\) 它是由点 \(x_0\) 加上和向量 \(a\) 成钝角的任意向量组成的。
- 注:半空间其实很好理解,就是对一个超平面进行了分割,也就是对一个无限延伸的空间进行了切分
注:接下来讲的几个凸集,可以通过图片就很容易判断了,具体的证明其实假设存在两个点 \(x_1\) 和 \(x_2\),然后套用仿射集、凸集、锥的定义看是否满足条件就行了。
[欧几里得球 Euclidean balls] 一个 \(R^n\) 中的(欧几里得)球是 \(B(x_c,r)=\{x\;|\; ||x-x_c||_2\leq r\}=\{x| (x-x_c)^T(x-x_c)\leq r^2\}\) , \(r>0\) 表示欧几里得范数,也就是 \(||u||_2=(u^Tu)^{1/2}\) 。欧几里得球是一个凸集。
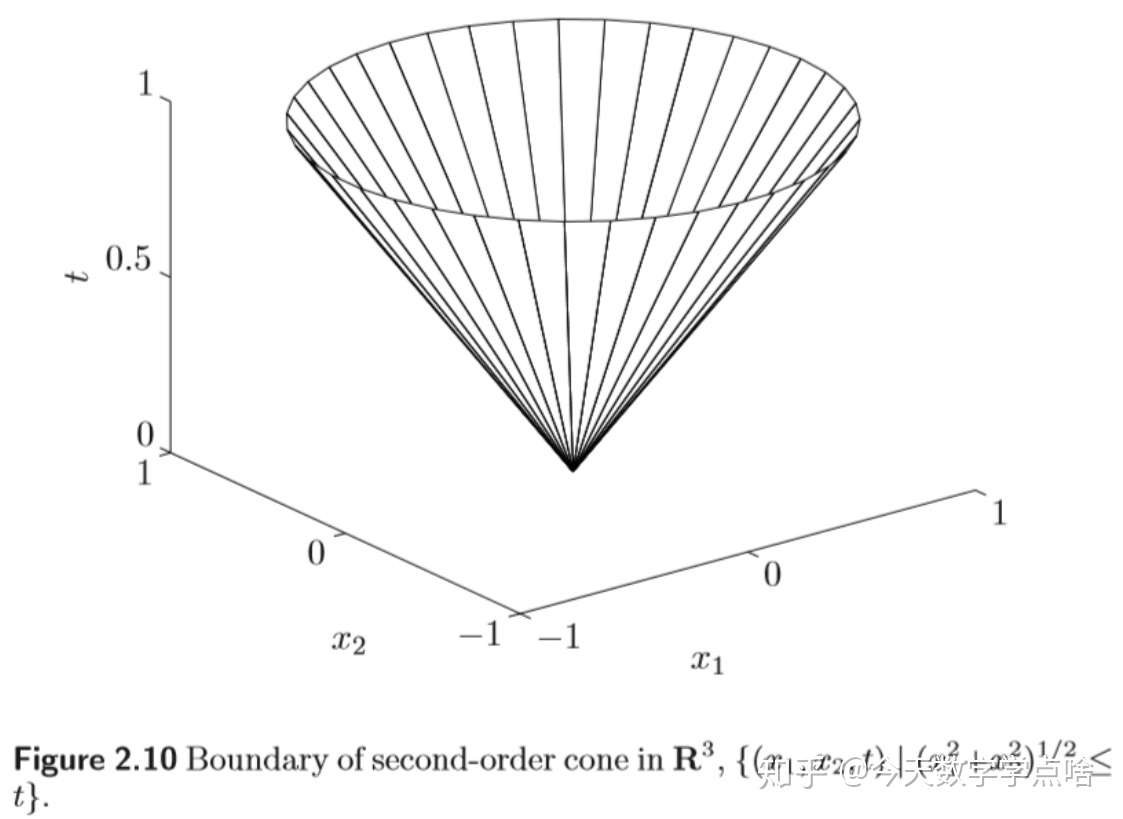
[球 norm ball,锥 norm cone] 令 \(\|\cdot\|\) 是 \(R^n\) 上的任意范数,norm ball 是集合 \(\{x| \| x-x_c\| \leq r\}\) 是凸的。norm cone 是集合 \(C=\{(x,t) | \|x\|\leq t\}\subseteq R^{n+1}\) .
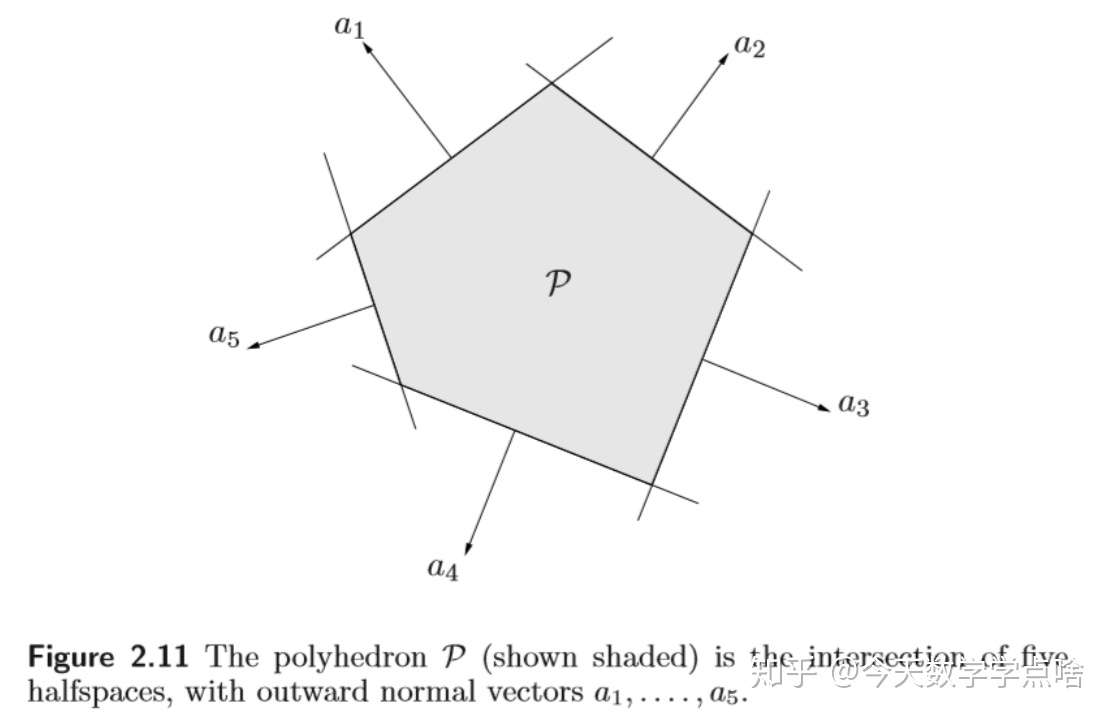
[多面体 Polyhedra] 多边形是有限个线性方程和不等式的解集 \(P=\{x| a^T_jx\leq b_j, j=1,...,m, c^Tx=d_j, j=1,...,p\}\) .
- 是多个半空间和超平面的交集
- 是凸集
[单纯形 Simplexes] 单纯形是多面体的另一个重要的类,令 \(k+1\) 个点 \(v_0,...,v_k\in R^n\) 是仿射独立的,意思是 \(v_1-v_0,...,v_k-v_0\) 都是线性无关的。这些点确定的单纯形是凸包 \(C=conv\{v_0,...,v_k\}=\{\theta_0v_0+...+\theta_kv_k\;| \; \theta \succeq 0,1^T\theta=1\}.\)
- 单纯形的仿射维数是 \(k\) ,也叫做 \(k\) -单纯形。
- 0-单纯形是点,1-单纯形是线段,2-单纯形是三角形,3-单纯形是四面体,而4-单纯形是一个五胞体。
三、保持凸性的运算
[交集] 交集保持凸性,如果 \(S_1,S_2\) 是凸的,那么 \(S_1\cap S_2\) 也是凸的。这个性质可以推广到有限个集合的交集。
[仿射函数] 一个函数 \(f: R^n\rightarrow R^m\) 是仿射的,如果它是一个线性函数和常数的和。也就是形如 \(f(x)=Ax+b\) , \(A\in R^{m\times n}\) , \(b\in R^m\) .
注:仿射函数,其实很容易理解,就可以看成是一个二维空间中的一个平面图形的伸缩和平移,只不过这里是对高维空间进行了统一。假设,在二维空间有一个三角形,你无论怎么做伸缩和平移,它仍然是一个三角形,而三角形属于单纯型,单纯型又都是凸的
如果 \(S\subseteq R^n\) 是凸的并且 \(f: R^n\rightarrow R^m\) 是一个仿射函数,那么 \(S\) 在 \(f\) 映射下的像 \(f(S)=\{f(x)| x\in S\}\) 是凸的。类似地, \(S\) 在 \(f\) 下的逆象也是凸的。
- 一个凸集的缩放 \(\alpha S\) 和平移 \(S+\alpha\) 是凸的.
- 一个凸集到它某个维度的投影是凸的: if \(S\subseteq R^m\times R^n\) , then \(T=\{x_1\in R^m| (x_1,x_2)\in S , for\, some\, x_2\in R^n\}\) is convex.
- 凸集的和是凸的。
- 凸集的积是凸的, \(S_1\times S_2=\{(x_1,x_2)|x_1\in S_1, x_2\in S_2\}\) .
- 凸集的部分和是凸的, \(S_1,S_2\in R^n\times R^m\) , \(S=\{(x,y_1+y_2)| (x,y_1)\in S_1, (x,y_2)\in S_2\}.\)
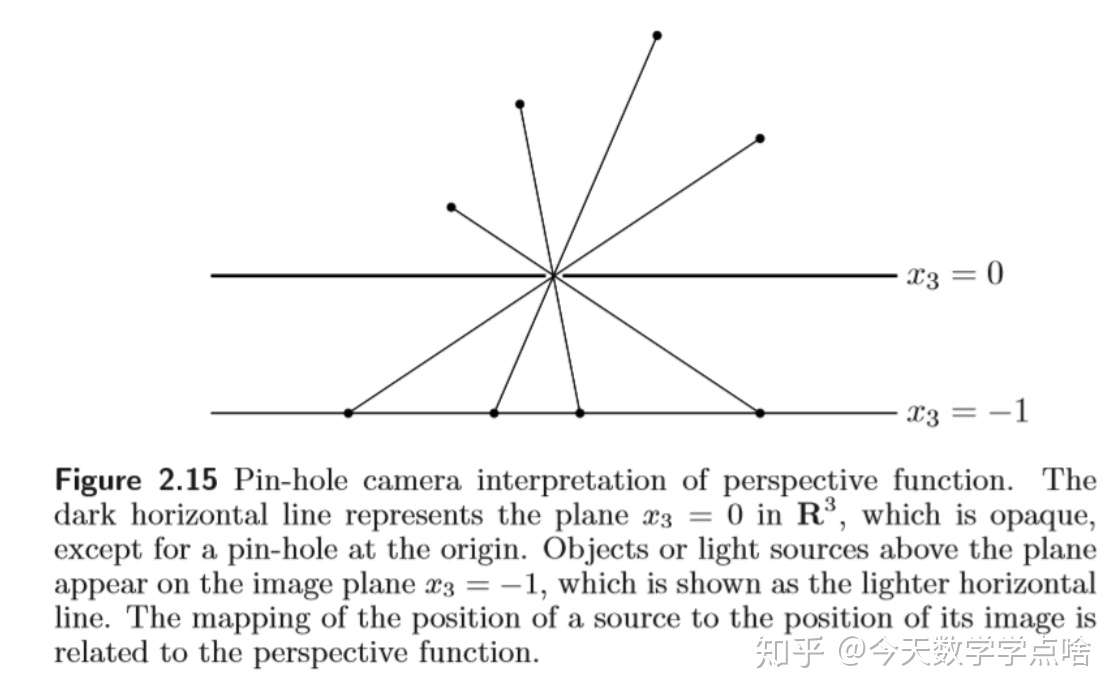
[透视函数 perspective function] 我们定义透视函数 \(P: R^{n+1}\rightarrow R^n\) , \(P\) 的定义域 \(domP=R^n\times R_{++}\) , \(P(z,t)=z/t\) .
注:透视函数其实也很容易理解,无非就是投影。依然拿二维空间举例,从透视函数的定义,可以看出,无非是对某一维进行了降维,也就是二维图像降维成了一维的,可以想象,三角形降维成一维的就是一条线段,如果是非凸非封闭的三角形透视之后就是有间隙的线段,也就是说透视之后非凸
\(R_{++}\) 是指正数的集合: \(R_{++}={x\in R|x>0}\)
- 透视函数可以缩放向量,或归一化向量——使其最后一个元素为1,然后去掉最后一个元素。
- 如果 \(C\subseteq domP\) 是凸的,那么 \(C\) 在 \(P\) 映射下的像 \(P(C)\) 也是凸的。
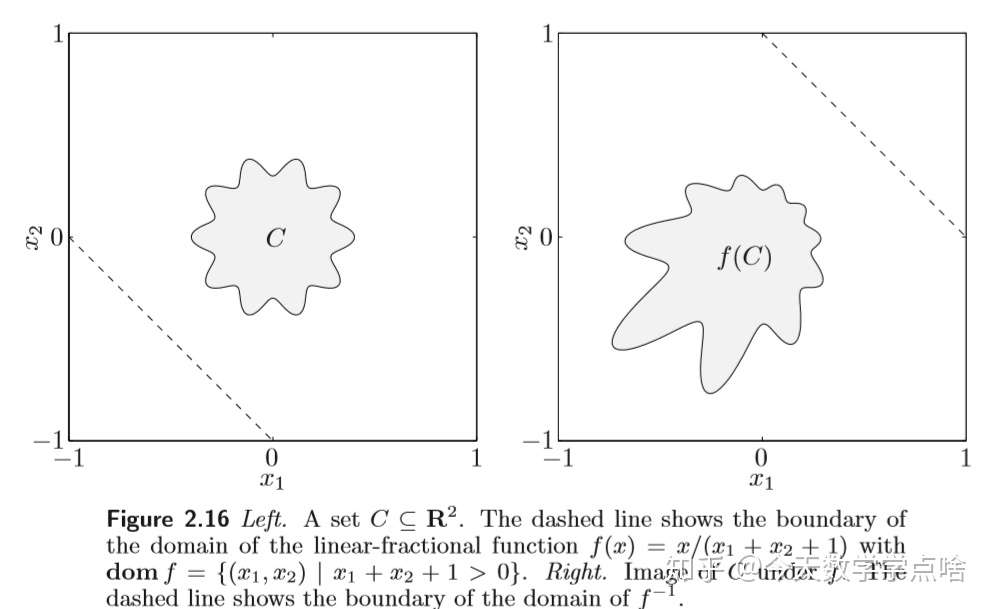
[线性-分数 函数 Linear-fractional function] 一个Linear-fractional function 是透视函数和一个仿射函数的复合。
注:线性分式,很好理解咯,无非就是伸缩平移之后再投影(降维),一个道理,仍然保持凸性
设仿射函数 \(g: R^n\rightarrow R^{m+1}\) 为 \(g(x)=\begin{bmatrix}A\\c^T\end{bmatrix}x + \begin{bmatrix}b\\d\end{bmatrix}\) . 其中 \(A\in R^{m\times n}, b\in R^m, c\in R^n, d\in R.\)
则函数 \(f: R^n\rightarrow R^m\) , \(f=P\circ g\) ,也就是
\(f(x)=(Ax+b)/(c^Tx+d)\) ,
$domf= {x|c^Tx+d>0} $
是一个Linear-fractional function。
- Linear-fractional function 保留凸性。
四、广义不等关系
[proper cone] 一个锥 \(K\subseteq R^n\) 称为 proper cone 如果它满足以下性质:
- K是凸的
- K是闭的
- K是实的(solid),也就是有非空的内部(interior)。
- K是尖的(pointed),也就是不含有线( \(x\in K, -x\in K \Rightarrow x=0\) ).
[广义不等关系] 是一个 \(R^n\) 上的偏序。令 \(K\) 是一个proper cone,定义:
注:广义不等式其实就是规定了两个比较对象的维度,而这种比较就需要考虑到各个维度的比较,比如 \(\begin{bmatrix} 1 \\ 2 \end{bmatrix}\) 和 \(\begin{bmatrix} 0 \\ 3\end{bmatrix}\) 就不可以比较,两者之差 \(\begin{bmatrix} 1 \\ -1\end{bmatrix}\)不属于锥内部了,比如 \(\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}\) 和 \(\begin{bmatrix} 0 \\ 1\end{bmatrix}\) 同样不可以比较,两者维度都不一样
\(x\preceq_K y \Longleftrightarrow y-x\in K\) .
\(x\prec_K y \Longleftrightarrow y-x\in intK\) .
- 当 \(K=R_+\) 偏序 \(\prec_K\) 就是普通的 \(R\) 上的 \(\leq\) 。
- 广义不等关系 \(\preceq_K\) 满足许多性质:加法不变,传递性,非负缩放不变,自反性,反对称性,取极限不变。
\(y-x\) 是以 \(x\) 为起点以 \(y\) 为终点的向量,画图就明白了。
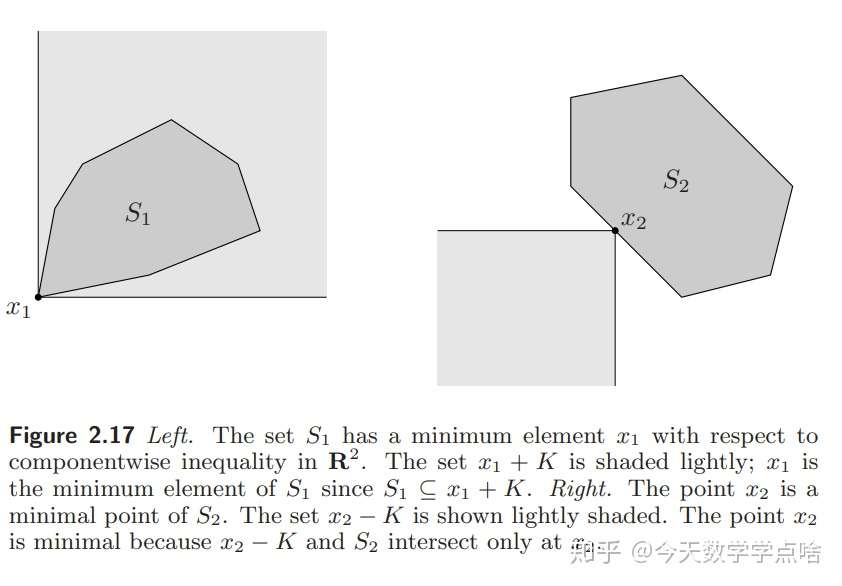
[最小元素 minimum] \(x\in S\) 是 \(S\) 中的最小元素,如果对每个 \(y\in S\) 有 \(x\preceq_K y\) . 最大元素同理。 一个集合中的最小(最大)元素如果有就是唯一的。
[极小元素 minimal] \(x\in S\) 是 \(S\) 中的极小元素,如果 \(y\in S\) , \(y\preceq_k x\) 仅当 \(y=x\) . 极大元素同理。一个集合中可以有多个极小(极大)元素。
注:为了便于理解,判断最小元素和极小元素可以从分量的角度去考虑,最小元素的所有分量都是最小的,比如比如 \(\begin{bmatrix} 1 \\ 2 \end{bmatrix}\) 和 \(\begin{bmatrix} 2 \\ 4\end{bmatrix}\),两个分量都是最小的 ;而极小元素可能只是某个分量为较小的,或者说极小元素的有些分量无法做出最小的判断,比如比如 \(\begin{bmatrix} 1 \\ 0 \end{bmatrix}\) 和 \(\begin{bmatrix} 0 \\ 1\end{bmatrix}\) ,第一个分量前一个大,第二个分量前一个小。可以通过下图自行从分量的角度理解
- 一个点 \(x\in S\) 是集合 \(S\) 的最小元素,当且仅当 \(S\subseteq x+K\) , 其中 \(x+K\) 表示所有大于或等于 \(x\) ( \(\preceq_K\) )的点。
- 一个点 \(x\in S\) 是集合 \(S\) 的极小元素,当且仅当 \((x-K)\cap S=\{x\}\) , 其中 \(x-K\) 表示所有小于或等于 \(x\) ( \(\preceq_K\) )的点。
五、分离超平面和支撑超平面 (Separating and Supporting Hyperplane)
[超平面分离定理] 令 \(C\) 和 \(D\) 都是非空且不相交的凸集, \(C\cap D =\emptyset\) . 那么存在 \(a\ne 0\) 和 \(b\) ,使得 \(a^Tx\leq b\) 对于所有的x \(\in C\) ,和 \(a^Tx\geq b\) 对于所有的 \(x\in D\) 。超平面 \(\{x| a^Tx=b\}\) 叫做集合 \(C,D\) 的分离超平面,它分离集合 \(C\) 和 \(D\) 。
如果把不等式的等号去掉就叫做严格分离。
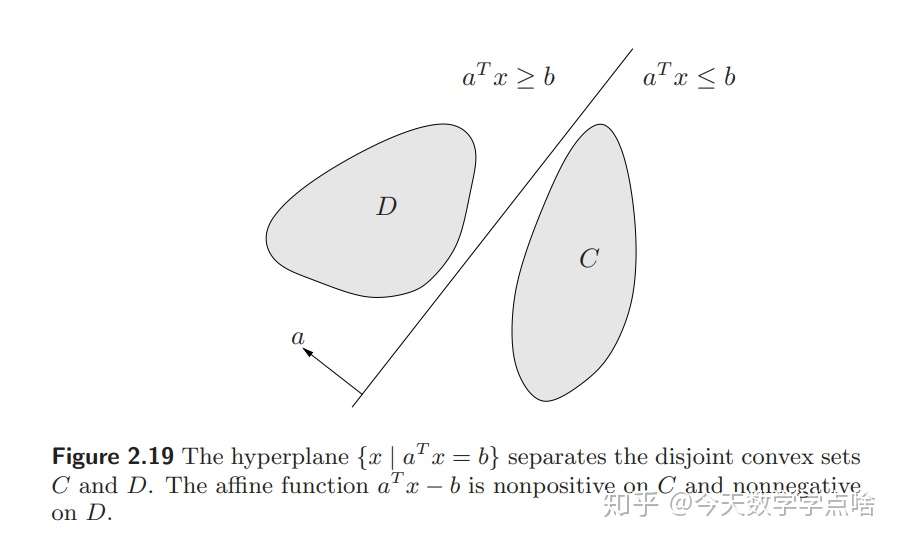
[逆超平面分离定理] 任意两个凸集 \(C,D\) ,其中至少一个是开集,它们不相交,当且仅当存在一个分离超平面。
[支撑超平面] 令 \(C\subseteq R^n\) , \(x_0\) 是一个位于边界 \(bd\,C\) 的点, \(x_0\in bd\,C=clC\backslash intC\) . 如果 \(a\ne 0\) 满足对所有 \(x\in C\) 有 \(a^Tx\leq a^Tx_0\) ,那么超平面 \(\{x| a^Tx=a^Tx_0\}\) 叫做 \(C\) 在点 \(x_0\) 的支撑超平面。
注:支撑超平面其实就是一个凸集找到一条切线,并且这个凸集要在这个切线分离的其中一个半空间内
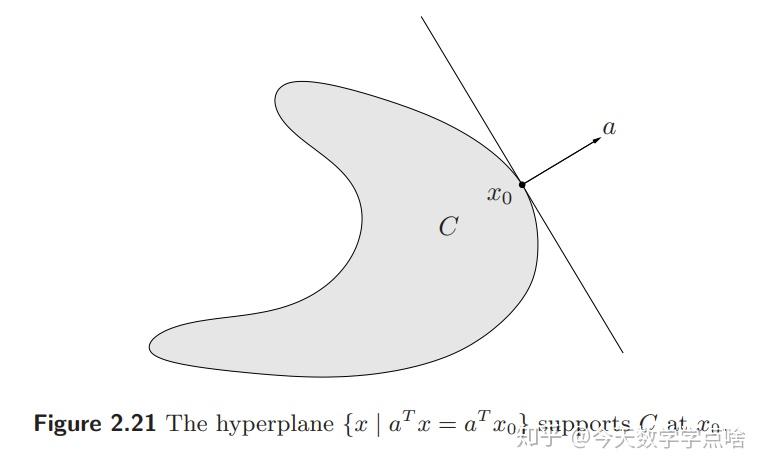
[支撑超平面定理] 对于任意非空凸集 \(C\) ,和任意点 \(x_0\in bd C\) 都有一个 \(C\) 在点 \(x_0\) 上支撑超平面。
[部分逆支撑超平面定理] 如果一个集合是闭的,有非空的内部,且在边界上的每个点处有支撑超平面,那么它是凸的。注:只针对凸集
六、对偶锥和广义不等关系
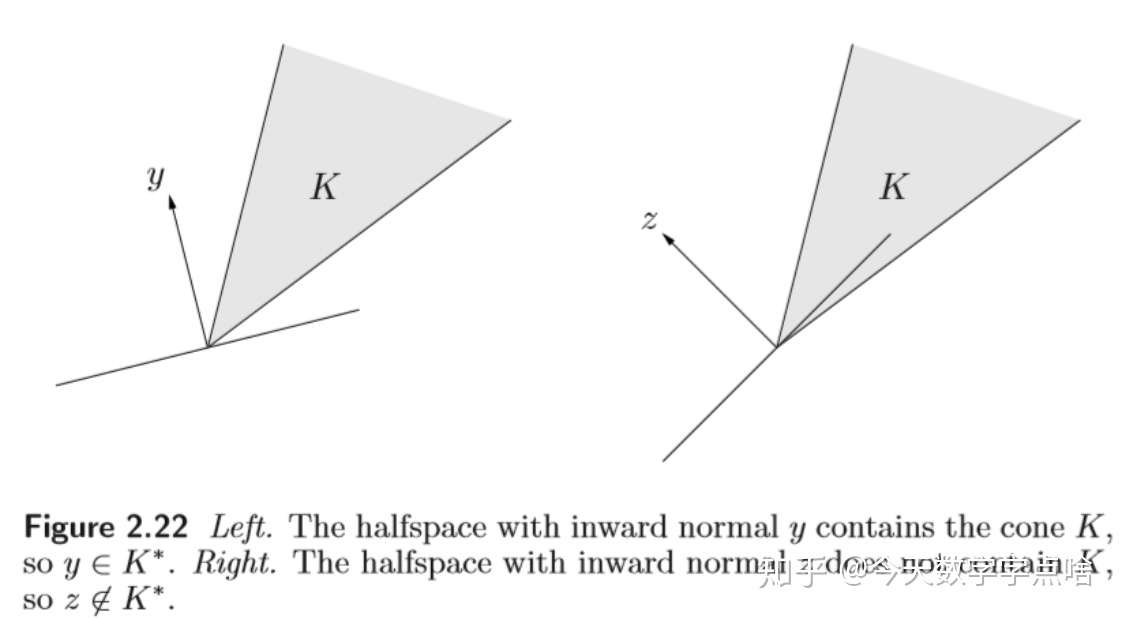
[对偶锥 Dual cone] 令 \(K\) 是一个锥,集合 \(K^*= \{y | x^Ty\geq 0, \; for all \; x\in K\}\) 叫做 \(K\) 的对偶锥。 \(K^*\) 是一个 锥,并且总是凸的,即使原来的锥 \(K\) 不是凸的。
注:其实很容易理解,就是从 \(x^Ty\geq 0\) 这个角度去考虑,可以把它看成是 \(x\) 和 \(y\) 的内积,这就是表明 \(x\) 和 \(y\) 形成的夹角小于 90° ,下图中法向量 \(z\) 和 锥\(K\) 的一部分形成了钝角,所以 \(z \notin k^*\)
向量 y和 K中任意向量x成锐角。
[对偶锥的性质]
- \(K^*\) 是闭且凸的。
- \(K_1\subseteq K_2\) 意味着 \(K^*_2\subseteq K^*_1\) .
- 如果 \(K\) 有非空的内部,那么 \(K^*\) 是尖的(pointed).
- 如果 \(K\) 的闭包是pointed 那么 \(K^*\) 有非空的内部。
- \(K^{**}\) 是 \(K\) 凸包的闭包。(所以如果 \(K\) 是凸且闭的,那么 $ K^{ ** }=K$ )注:对偶的对偶是原锥
以上性质表明,如果 \(K\) 是一个 proper cone,那么它的对偶锥 \(K^*\) 也是 proper cone,并且 \(K^{**}=K\) .
[对偶广义不等关系] 令锥 \(K\) 是凸且proper的,由它给出一个广义不等关系 \(\preceq_K\) 。然后它的对偶锥也是proper的,于是也给出一个广义不等关系 \(\preceq_{K^*}\) ,作为 \(\preceq_K\) 的对偶。有以下性质:
- \(x\preceq_K y\) 当且仅当 \(\lambda^Tx\leq \lambda^Ty\) , \(\forall \lambda\succeq_{K^*} 0\) .
- \(x\prec_K y\) 当且仅当 \(\lambda^T x< \lambda^Ty\) , \(\forall \lambda\succeq_{K^*} 0\) , \(\lambda\ne 0\) .
注:对于最小元素的对偶性质和极小元素的对偶性质的具体理解,可以参考这篇博客https://www.zhihu.com/question/264853229
[最小元素的对偶性质] 根据不等关系 \(\preceq_K\) , \(x\) 是 \(S\) 中的最小元素,当且仅当对于所有的 \(\lambda \succ_{K^*} 0\) , \(x\) 是唯一使得 \(\lambda^T z\) , \(z\in S\) 取最小值的元素。
用几何的观点看,这意味着对于任意 \(\lambda\succ_{K^*}0\) ,超平面 \(\{z| \lambda^T(z-x)=0\}\) 是 \(S\) 在点 \(x\) 上的严格支撑超平面(严格就是超平面和 \(S\) 只在点 \(x\) 相交),注意此处 \(S\) 不需要是凸集。
注:依然是从内积角度去看待这个问题
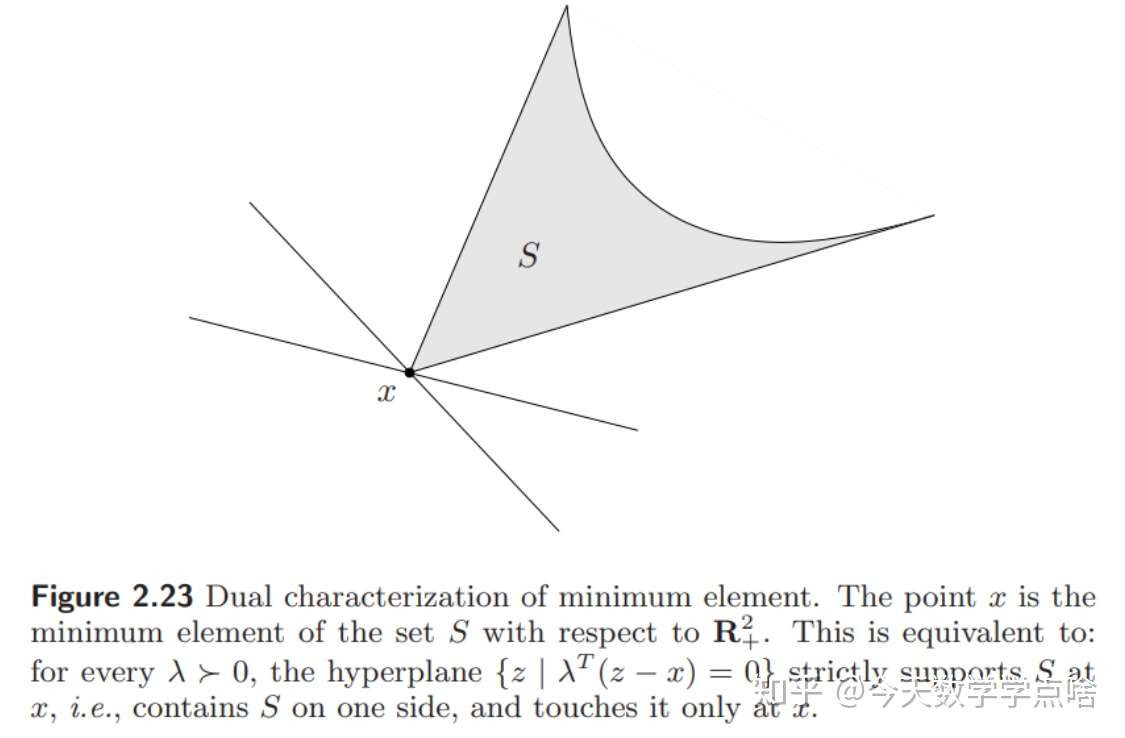
[极小元素的对偶性质] 如果存在 \(\lambda \succ_{K^*}0\) 并且 \(x\) 使得 \(\lambda^T z, z\in S\) 取最小值,那么 \(x\) 是极小值。
注:这样去理解下述图像可能容易点,也就是 \(x_1\) 是 \(\lambda_1\) 方向上的最优解。这样有什么好处呢,比如对于一个 \(\lambda_1\) 和 \(\lambda_2\),我们想知道 \(\lambda_1 x_1\) 和 \(\lambda_2 x_2\) 的大小,这是很困难的,但是我们知道 \(\lambda_1\) 和 \(\lambda_2\) 属于 \(K^*\),那么我们比较 \(\lambda_1\) 和 \(\lambda_2\) 在 \(K^*\) 上的大小就行了。
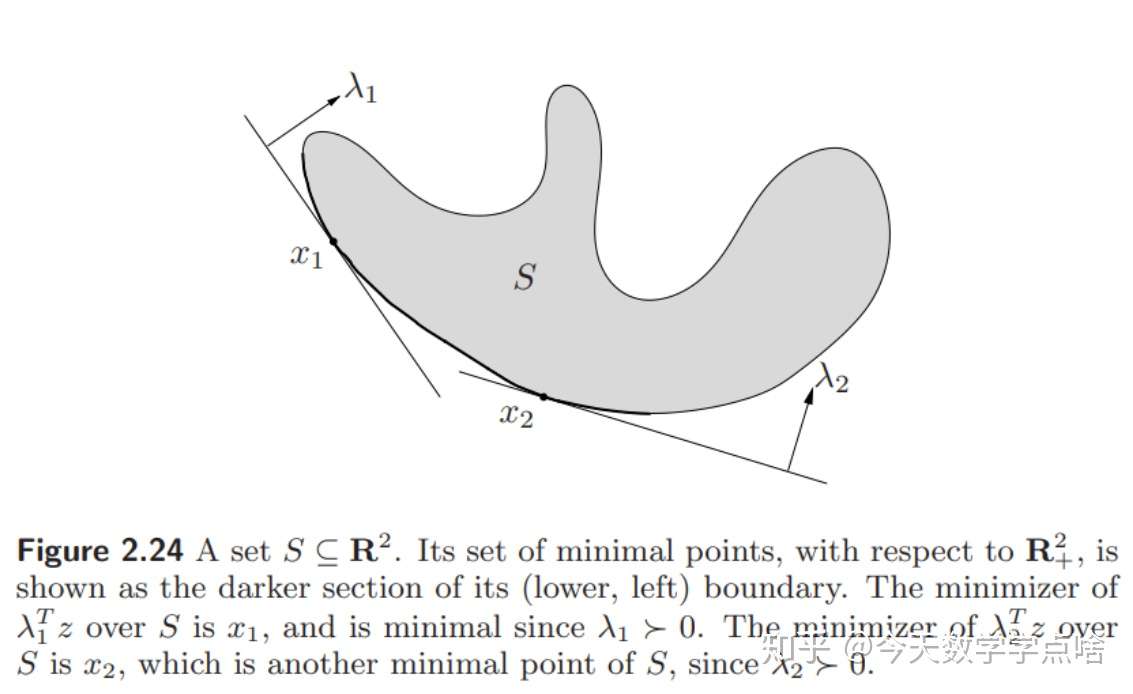
定理反过来是不对的,也就是存在这种情况: \(x\) 是极小元素,但不能使任何的 \(\lambda^Tz, z\in S\) 取最小值,如图:
方形阴影是锥 \((x-K)\) , 回顾广义不等关系那节: \(x\) 是极小元素,当且仅当锥 \((x-K)\) 与 \(S\) 仅在 \(x\) 点相交。同时,对于任意的 \(\lambda\) , \(\lambda^Tx\) 都不是最小的,最小值总是在凸的地方取到。
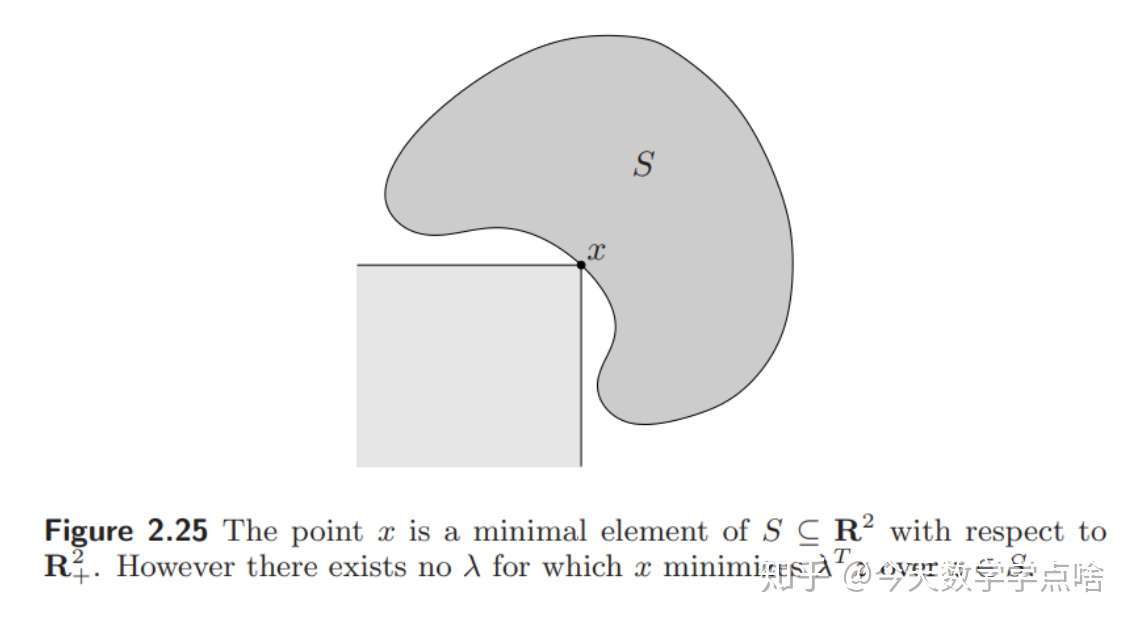
如果加上条件: \(S\) 是凸集,那么以上逆定理就正确了,对于任意极小元素 \(x\) ,有非零的 \(\lambda\succeq_{K^*}0\) 使得 \(\lambda^Tz, z\in S\) 在 \(x\) 处取得最小值。
- 但是如果此时,把条件强化为 \(\lambda\succ_{K^*}0\) 就又不对了,如图:

七、最小元和极小元和对偶锥的再解释
复习:最小元与极小元
下面两幅图分别表示最小元和极小元
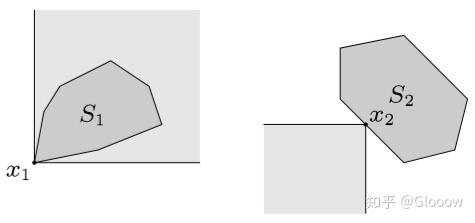
利用对偶锥,我们可以获得最小元的等价定义,即
\(x\) 是集合 \(S\) 关于 \(\preceq_{K}\) 的最小元 \(\iff\) 对任意的 \(\lambda \succ_{K*} 0\),\(x\) 为 \(\lambda^Tz\) 在集合 \(S\) 上的唯一最小解
什么意思呢?也就是说任意的 \(\lambda\in K^*\),实际上都代表了一个法向量,也就是一个支撑超平面。如果 \(x\) 是最小元,则意味着对任意一个 (\(K^*\)所定义的) 支撑超平面来说,\(x\) 都是支撑点,就像下面这条幅图一样
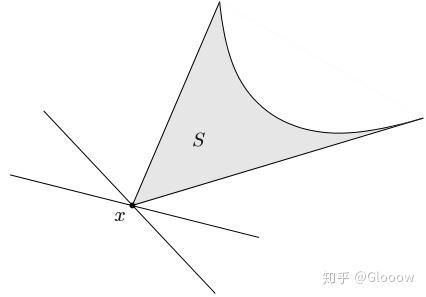
而极小元的定义是什么呢?
- 充分条件:若对于某些 \(\lambda \succ_{K*} 0\),\(x\) minimizes \(\lambda^Tz\) over \(S\),\(\Longrightarrow\)\(x\) 为极小元
- 必要条件:\(x\) 为凸集\(S\) 的极小元,\(\Longrightarrow\) 存在非 0 的 \(\lambda \succ_{K*} 0\) 使得 \(x\) minimizes \(\lambda^Tz\) over \(S\)
我们来看充分条件,只需要存在某一个 \(\lambda\in K^*\),使得 \(x\) 为对应支撑超平面的支撑点就可以了。比如下面这幅图,蓝色的点,我们可以找到这样一个蓝色的支撑超平面,使其为支撑点,所以它就是一个极小元;而对于红色的点来说,无论如何不可能找到一个支撑超平面,使其为支撑点,因此他就有可能不是极小元,因为这只是充分条件(对这个例子来说他就不是极小元)。
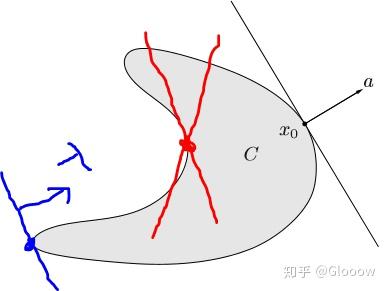
简单总结一下:
- 最小元:无论沿着锥 \(K^*\) 里边哪一个方向走,\(x\) 都是最小值点,那么他就是最小元;
- 极小元:如果沿着其中某一个方向走,\(x\) 是最小值点,那么他就是极小元。
参考文献:Stephen Boyd, Lieven Vandenberghe: Convex Optimization


