计应193第二组吕志江郑州地铁收费系统
| PSP阶段 | 预计花费时间(小时) | 实际花费时间 |
| 计划 | 2 | 2 |
| 明确需求和其他相关因素,估计每个阶段的时间成本 | 2 | 2 |
| 开发 | 22 | 2 |
| 需求分析 | 2 | 2 |
| 代码规范 | 1 | 1 |
| 具体设计 | 2 | 2 |
| 具体编码 | 12 | 12 |
| 代码复审 | 2 | 2 |
| 测试(自测、修改代码、提交修改) | 3 | 3 |
明确需求和其他相关因素,估计每个阶段的时间成本:
通过对地铁项目的了解(原文链接:现代软件工程讲义 个人项目和结对项目练习 地铁)。得出以下信息:

- 计费算法仅仅是随意写的。具体收费标准要依据郑州市地铁计费标准计算。由于计费标准规定是按照公里数进行计费的。而难以获取详细的各站点之间的距离参数,所以改成按站点计费。
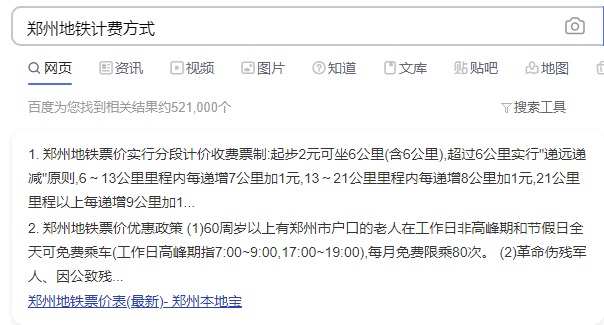
- 对于最短路径算法,通过研究发现是这个项目的核心内容。计费算法与查找最短路线算法都要依据其而计算。应优先进行考虑。
- 查找最短路线算法,需要知道最短路线,即可将最短路线打印输出。
- 对于各个站点的代码转换计划使用类进行表示。属性应具备:当前站点、上一临近站点、下一临近站点、是否为换乘点、当前站点所属线路等等属性及对应的方法。
需求分析:
- 用户要进行输入操作,应具备接收输入的功能。
- 要在后台计算出起点和终点的最短距离,应该计算出路径所经过的站点总数,选择最短的一条路径,并将其值传递给计算计费算法模块,同时输出所需花费。
- 要将最短路线打印输出,需要在寻找最短路径时加以留心,将各个结果存储下来,再提取所需的最短路径,进行处理,得到最短路线方案。
具体设计:
原计划写接口,再写类,将所有站点转换成类,使用集合进行管理。对于在同一条线上的站点,直接计算两个站点之间的差值的绝对值就知道了最短路线以及最短距离。但是不在一条线上呢?如果是跨一条线(例一号线转三号线),我们可以找到这两条线之间的换乘点,进行一次换乘,实现最短路线。但是如果是跨两条线呢?(例一号线转三号线再转五号线)。再延续之前的算法:找到距离出发点最近的换乘点,再找到距离终点最近的换乘点,再计算这两个换乘点之间的距离。但是会出现:下图情况(从东十里铺出发去北二十里铺,图一跨两条线,共十四站,图二跨一条线,十五站)

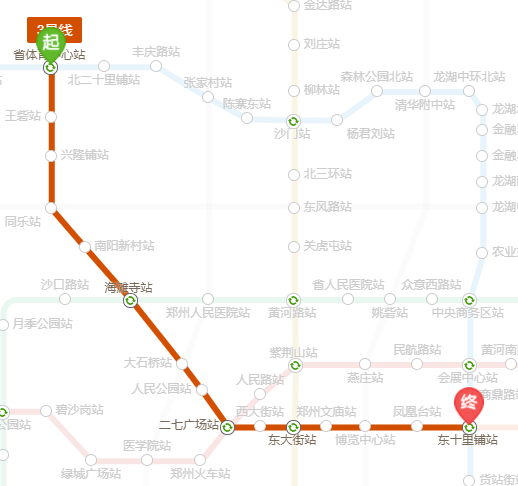
由此可知:并非跨线少就是最短路线,有时候跨线多了反而还是最短路线。所以不能使用简单的算法。这个算法成为了我们前进路上的一块石头。原计划使用A*算法(通过不断计算当前点和终点的直线距离,从而一步步指引当前点到达终点的算法)。然而无法计算当前点和终点的距离。需要知道各个站点之间的距离参数。
研究陷入了困境。
经过上网查找资料,发现了Dijkstra算法。这个算法非常巧妙,它并不关注终点在哪里,它是从起点出发,然后寻找最短路线去遍历整张图,直到,有一条路线碰到了目标点,那此时,最短路线便被找到了。由此又引入了图的概念,图是一种程序结构。图。在此处可理解为郑州地铁路线图。
该算法是:从起点出发,尝试去走到距离它最近的相邻节点。当它比较过后,会移动到最近的相邻节点上,然后再以此为“根据地”,再向当前节点的相邻节点探索,,同时与之前的路径比较,就是第一轮探索,我知道了去其他点要多远,当我在“根据地”向周围探索时,如果总共走的路径要比第一轮探索的路径要远,那我就不走了,走第一轮探索的那些路径。这样由会找到新的根据地,再重复上述步骤。找到最近的,就停下来。(好难呀,难怪视频里的老师讲的时候频频叹气。)然后不断寻找,直到碰到目标点,则最短路线就被找到了。
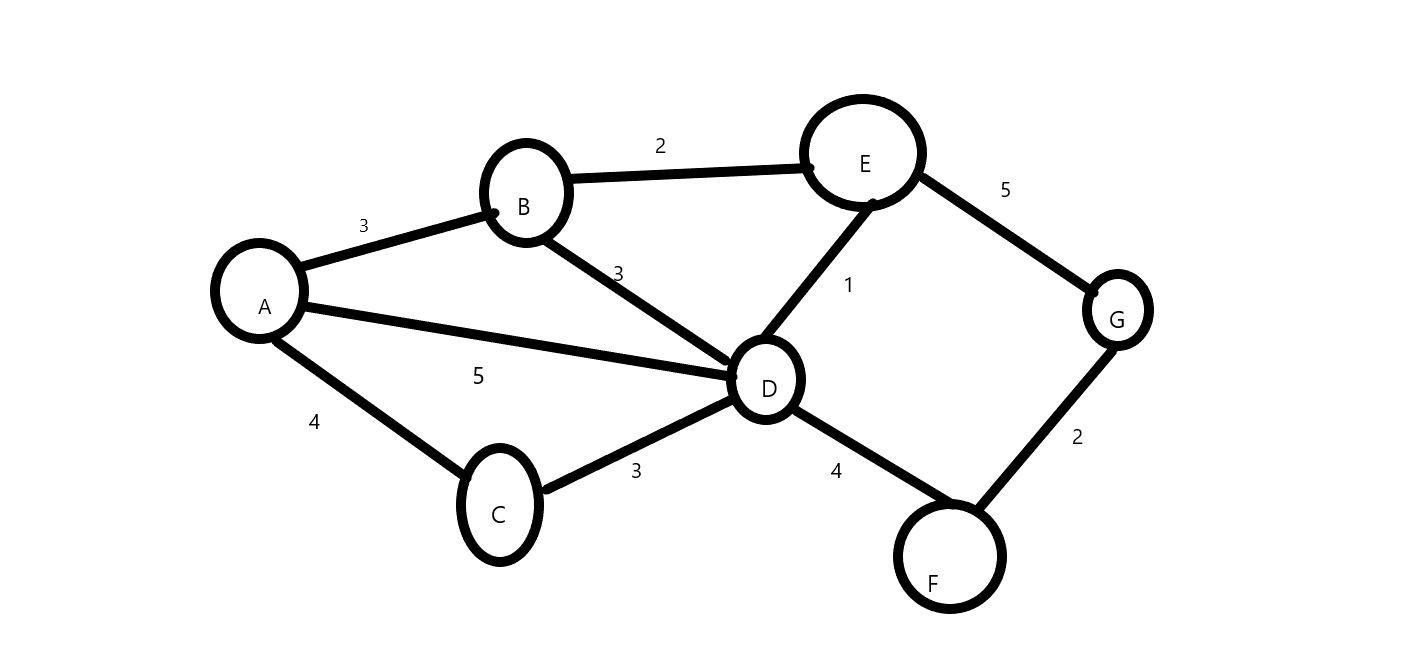
如上图,假设从A去G,那么最短路线是:A->B->E->G。所经过路径长度为:3+2+5=10。那么这条路径(A->B->E->G),其同时也被节点:A、B、E、G共享。那么A->E的最短路路径也一定在这条路径上。B->G的最短路径也在这条路径上。
再来看另一种情况:假设目标是找到A->D的最短路径。那么在刚开始:A会寻找去它相邻节点的最近的路径。它会在A->B 、A->D、A->C中查找。然后发现了A->B最近。于是它就去了B点,然后再次查找:B->D、B->E。然后发现B->E的路径是最短的,但是,A->B->E要大于A->C,这时我们就选择走A->C。并且以C作为新的“根据地”。这个时候我们可以将B节点拿走,拿出这张图,因为我们有了A->E的最短路径,而B节点在这个路径上,所以B节点暂时没有存在的必要了(也许会有人说,那还有B->D的路径呢!在这张图中A->B->E->D与A->B->D所走过的路径相等,所以等价,所以可以拿走。倘若|BD|=2,那A->B->D与A->B->E也等价,也可以拿走。再谈若|BD|=0.5,那当节点走到B之后的下一步,一定是B->D此时路线A-B-D-E要小于A-B-E。简而言之,当点B被作为“根据地”之后,再向下一步进发,B点便可以视作已经找到的最短的路径,便可以不做考虑)。再次寻找去相邻节点的最近的路径,发现有A->C->D(7)和A->B->D(6)以及A->B->E(5)还有A->D(5)这些路线可走,所以我们走了A->D或者A->B->E。假设走的是AD,那么我们会知道从D去F,是A->D->F(9),我们还有A->B->E->G(10)可走.于是我们走了A->D->F。至于A->B->E->D和A->D->E,不走,因为没有探索到新的点。D和E都是已经到达了的点。再走没意义。同时我们碰到了目标节点G,那么由A到G的最短距离便是A->B->E->G。再细细品一品,想一想。
具体编码:
根据上面的分析,我们要开始编码了。首先得有一张上面的图吧。那么我们还是以上面的图为例,写对应的算法程序(最后将上图替换成郑州地铁图,即可。)
上图是一张图,转换成代码语言。。。经过查阅资料,发现图的代码表示(以JAVA为例),是用二维数组表示的。其术语名为邻接矩阵,这样一来,接口也不用写了,实现类、集合统统不写了。
char[] jiedianbiao = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' }; //邻接矩阵(各节点间的距离) int [] [] linjie = new int [jiedianbiao.length][jiedianbiao.length]; final int N = 65535; //表示不可链接 linjie[0] = new int [] {N,3,4,5,N,N,N};//A到各点的距离 linjie[1] = new int [] {3,N,N,3,2,N,N};//B到各点的距离 linjie[2] = new int [] {4,N,3,N,N,N,N};//C到各点的距离 linjie[3] = new int [] {5,3,3,N,1,4,N};//D到各点的距离 linjie[4] = new int [] {N,2,N,1,N,N,5};//E到各点的距离 linjie[5] = new int [] {N,N,N,4,N,N,2};//F到各点的距离 linjie[6] = new int [] {N,N,N,N,5,2,N};//G到各点的距离
上述代码中,将各点之间的距离都用二维数组表示了,不相邻的之间的距离用65535记。
接下来需要创建几个标记信息。用来存储一些标记:
| 节点: | A | B | C | D | E | F | G |
| 是否已选(是否已经作为"根据地") | T | F | F | F | F | F | F |
| 距离出发点的距离 | 0 | 3 | 4 | 5 | N | N | N |
| 上一级节点是 | / | -1 | -1 | -1 | -1 | -1 | -1 |
说明:
- 是否已选行:T表示已经选择(已经遍历过、已经作为“根据地”过)
- 距离出发点的距离:当前节点距离出发点的最短距离
- 其上一级节点是:值是对应节点的下标。(因为是用数组进行存储的)
- 每一次遍历时:
- 会先找当前节点相邻的节点,将两条路都走一遍,然后找到最近、未被访问的节点。更新距离出发点的距离信息。
- 然后走到最近的节点上,然后将该节点的是否已选状态改成T。同时更改其上一级节点信息。
- 重复以上
- 当前表中的数据表示A为出发点,此时的各种数据。
接下来开始遍历:
第二步为:找到A->B、A->C、A->D,更新距离信息(本次不用更新),然后走到B节点,更改B节点以及与B节点相邻的节点的信息。包括:上一级节点信息为1。距离信息为6、5更改后的信息如下:
| 节点: | A | B | C | D | E | F | G |
| 是否已选(是否已经作为"根据地") | T | T | F | F | F | F | F |
| 距离出发点的距离 | 0 | 3 | 4 | 5 | 5 | N | N |
| 上一级节点是 | / | 0 | -1 | 1 | 1 | -1 | -1 |
第三步为:查找表中距离一栏,在未被选择的节点中(状态为F且距离最短的点为目标点)。此时为C点,然后走到C节点,更改C节点以及与C节点相邻的节点的信息。包括:上一级节点信息为1。距离信息因为A->B->D路线的距离要比A->D远,所以不做更新。更改后的信息如下:
| 节点: | A | B | C | D | E | F | G |
| 是否已选(是否已经作为"根据地") | T | T | T | F | F | F | F |
| 距离出发点的距离 | 0 | 3 | 4 | 5 | 5 | N | N |
| 上一级节点是 | / | 0 | 0 | 0 | 1 | -1 | -1 |
第四步为:查找表中距离一栏,在未被选择的节点中(状态为F且距离最短的点为目标点)。此时为D点,然后走到D节点,更改D节点以及与D节点相邻的节点的信息。包括:上一级节点信息为1。E、F距离信息。因A->D->E要远于A->B->E,所以不做更改。更改后的信息如下:
| 节点: | A | B | C | D | E | F | G |
| 是否已选(是否已经作为"根据地") | T | T | T | T | F | F | F |
| 距离出发点的距离 | 0 | 3 | 4 | 5 | 5 | 9 | N |
| 上一级节点是 | / | 0 | 0 | 1 | 1 | 3 | -1 |
第五步为:查找表中距离一栏,在未被选择的节点中(状态为F且距离最短的点为目标点)。此时为E点,然后走到E节点,更改E节点以及与E节点相邻的节点的信息。包括:上一级节点信息为1。G距离信息。更改后的信息如下:
| 节点: | A | B | C | D | E | F | G |
| 是否已选(是否已经作为"根据地") | T | T | F | T | T | F | F |
| 距离出发点的距离 | 0 | 3 | 4 | 5 | 6 | 9 | 10 |
| 上一级节点是 | / | 0 | -1 | 1 | 1 | 3 | 4 |
那么此时便找到了到达节点G最短的路径。
具体编码不做展示(仅分享个人在调试中的一张截图,目标节点图为上面的节点图);
辅助视频:戳我
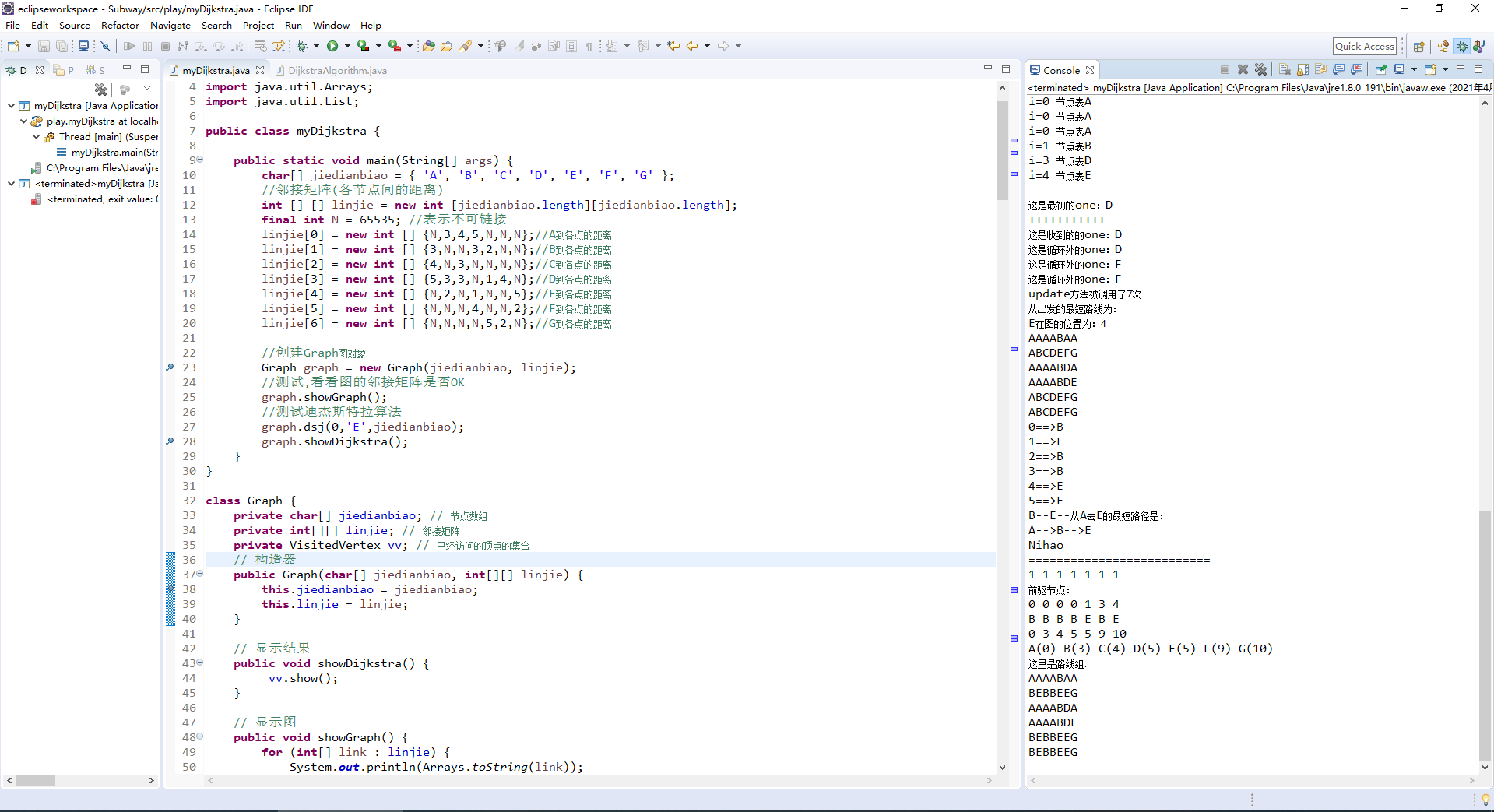
代码复审
在测试中问题还是比较多的。自己打断点用debug模式修改。以及写了很多输出语句来查找BUG。总归还是实现了算法。
测试
就这张图而言,也是经过了很多测试。但是还有部分测试没有覆盖到。将地铁图替换后应该能找到更多改进的地方。
总结
这个项目刚听到的时候没有什么感觉。就是细细一想,才发现都是问题。不过好在分析问题还算可以。找到了问题的核心。同时这个项目也告诉我,方向要更重要。需求分析在软件开发的过程中十分重要。必须要认真仔细。在具体实现的环节。查资料、改BUG。这些流程都是好像很简单->遇到困难停下开发进度->仔细研究->豁然开朗。坚持。继续努力。




