补充作业
第八周:
1、D2等于2时,第2趟排序结果是?(2分)

排序结果13 27 4 49 38 55 48 65 97 76
2、计算题:
1.有1023个结点的完全二叉树,其高度是多少?叶结点数是多少?(2分)
2.高度为h的完全二叉树至少有多少个结点?至多有多少个结点?(2分)
3.已知一棵度为m的树中有n1个度为1的结点,n2个度为2的结点,…,nm个度为m的结点,问该树中有多少个叶结点?(2分)

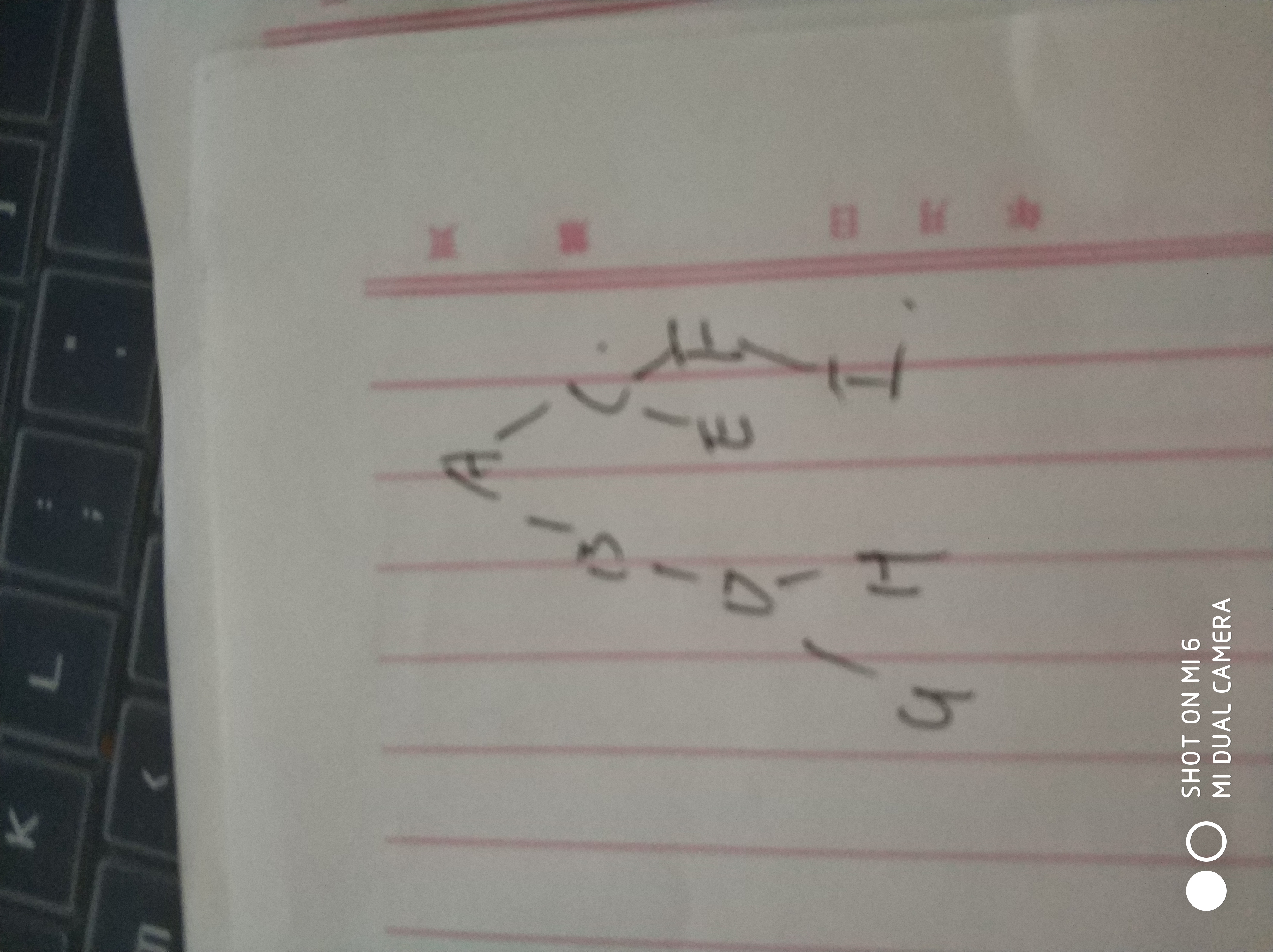
3、若已知中序和先序序列,计算二叉树结构
例:已知一棵二叉树的先序序列和中序序列分别为ABDGHCEFI 和 GDHBAECIF,试确定二叉树结构。(5分)
第十周
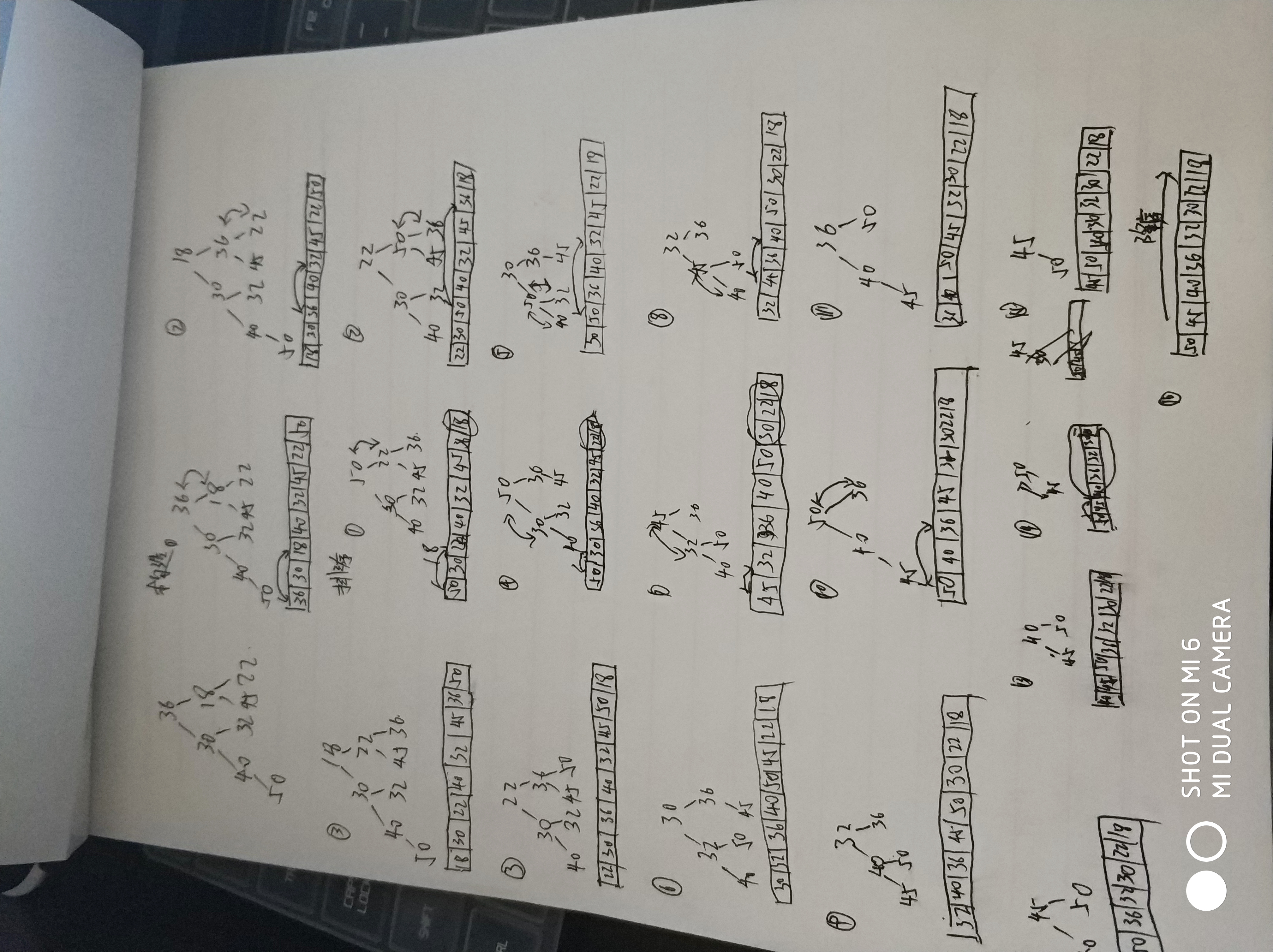
堆构造与排序 根据关键字序列:36,30,18,40,32,45,22,50,构造一颗小顶堆,并排序?
画出构造堆过程(树+数组)
第十一周
时间复杂度分析,用大O记法写出下面各题的时间复杂度:
(1)
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
for(k=1;k<=j;k++)
(2)
void fun(int n) {
int i=l;
while(i<=n)
i=i10;
}
(3)
int i, j,sum;
i=0;
j=0;
sum = i+j;
(4)void fun (int n){
int i=0;
while(ii*i<=n)
i++;
}
1道题1分,共计4分。
O(n^3)
O(lg (n))
O(1)
O( 3次根号下n)
已知线性表具有元素{5,13,19,21,37,56,64,75,80,88,92},如果使用折半查找法,ASL是多少?
(本题目2分,要求写出结题过程)
ASL=(1+22+34+4*4) / 11 = 33/11= 3


第十二周 十一链表练习

第十二周 最小生成树 1.画出Prim算法的最小生成树的生成过程
2.画出Kruscal算法的最小生成树的生成过程
3.计算最小权值
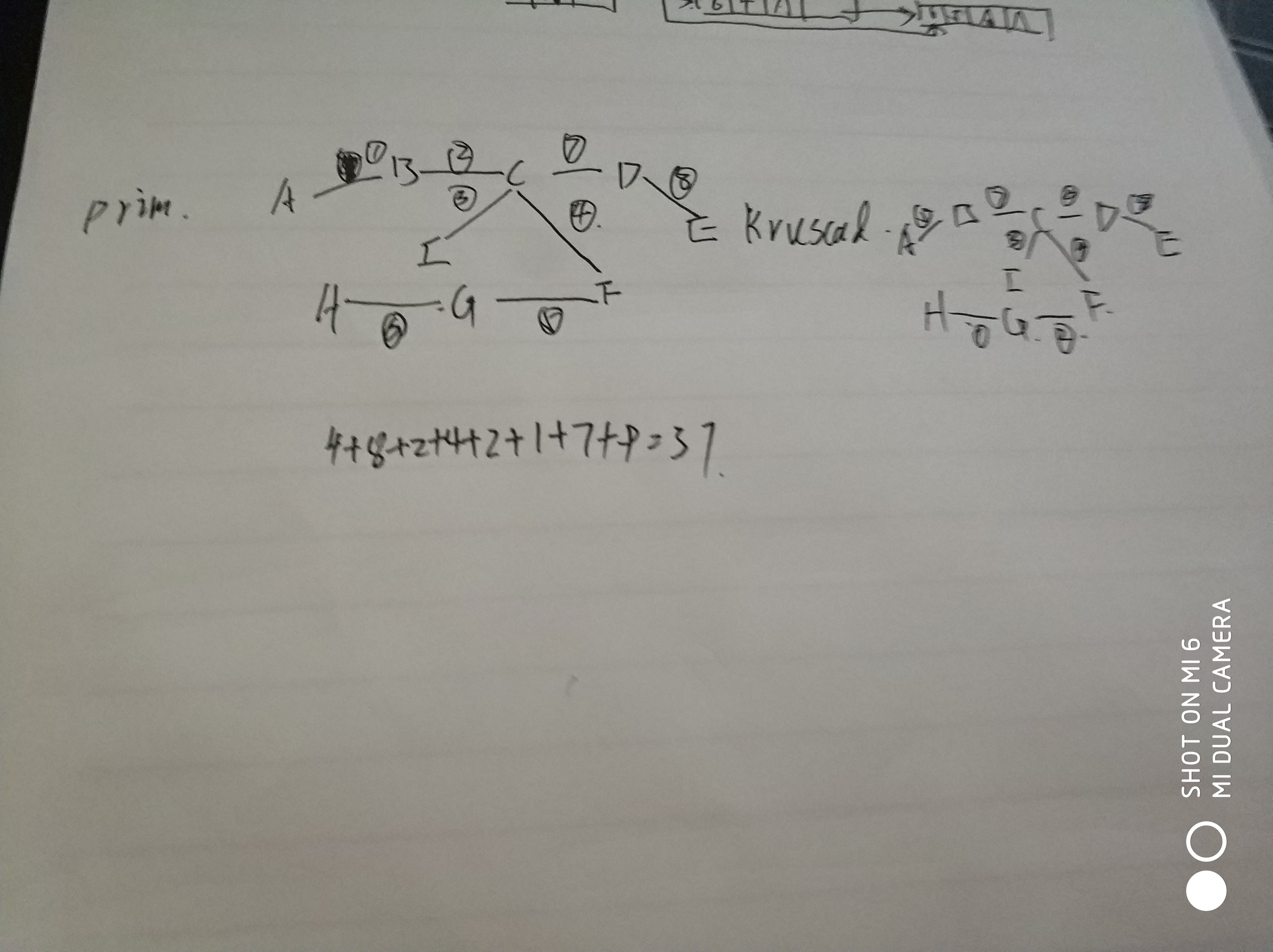
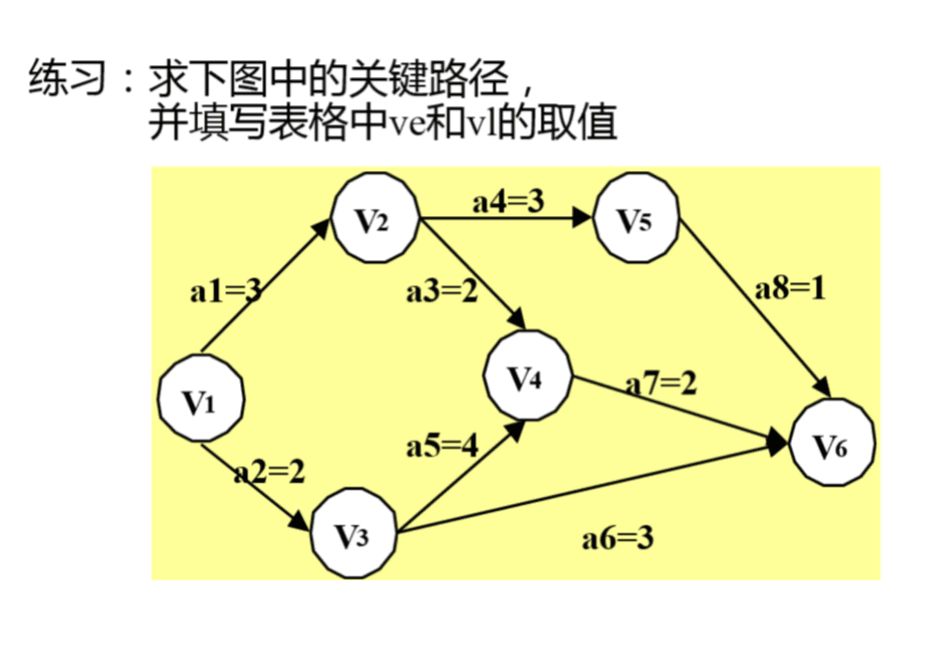
第十四周 AOE练习 1、求关键路径,v1和ve的值并写出具体步骤
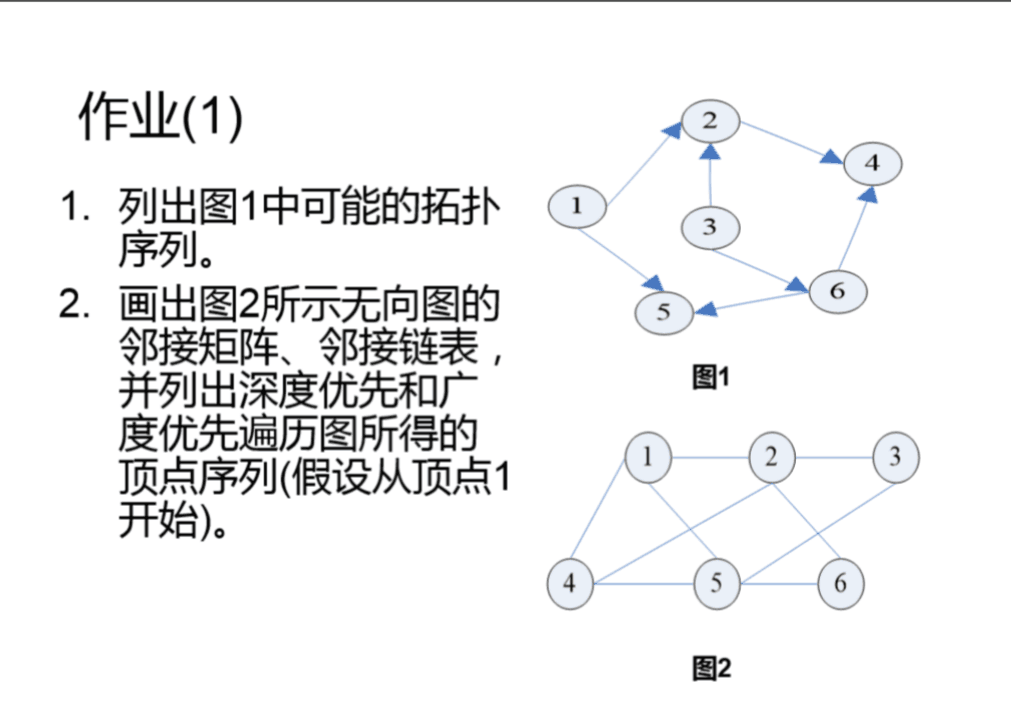
2、画出图一可能的拓扑序列
3、画出图二所示无向图的邻接矩阵、邻接链表,并列出深度优先和广度优先遍历图所得的顶点序列。
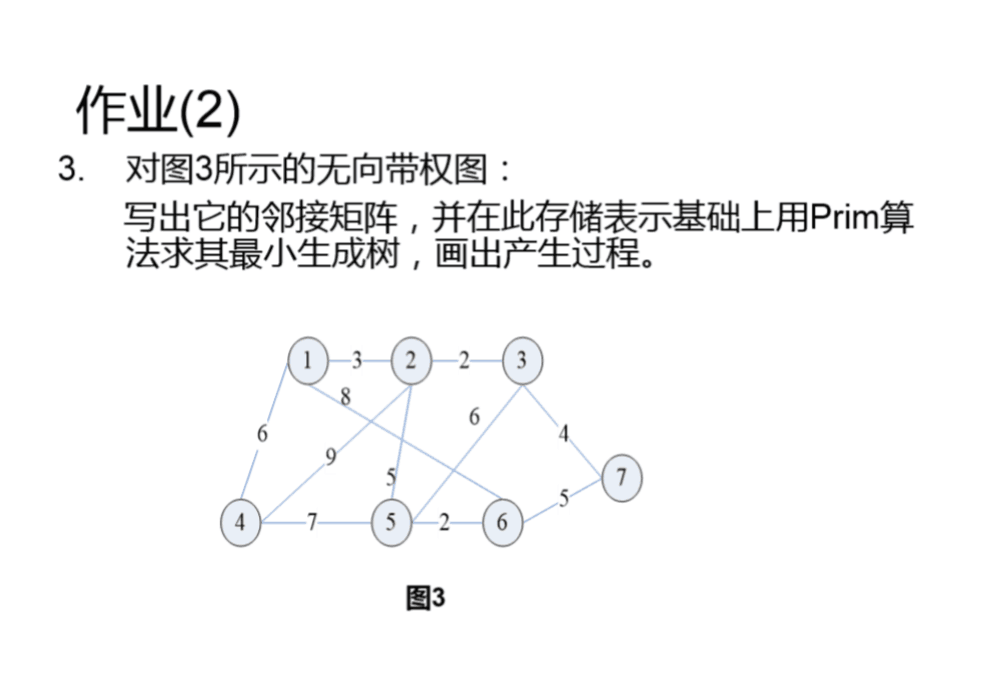
4、写出图三的邻接矩阵,并用prim算法求最小生成树,画出产生过程


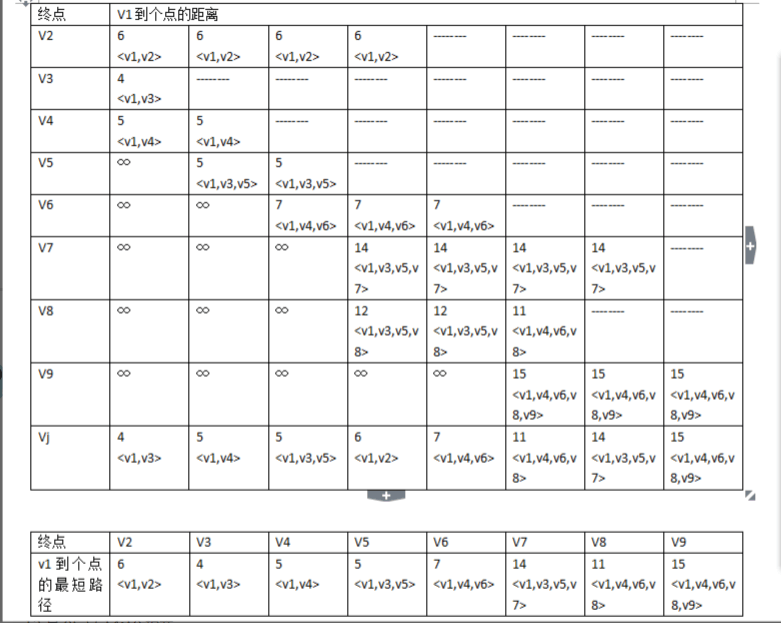
第十四周 Dijkstra(迪杰斯特拉)算法测试 使用Dijkstra(迪杰斯特拉)算法计算单源(V1出发)最短路径。
图2是课堂介绍的示例。
要求
(1)写出V1到各个顶点的最短路径
(2)要求写出最短路径计算过程(类似于图2)
评分(满足4分):
(1)结果正确得2分
(2)过程正确得2分