浅析拉格朗日乘数法及其对偶问题

拉格朗日乘数(Lagrange Multipliers)法

  在数学最优问题中，拉格朗日乘数法（以数学家约瑟夫·路易斯·拉格朗日命名）是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有n个变量与k个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题，其变量不受任何约束。这种方法引入了一种新的标量未知数，即拉格朗日乘数：约束方程的梯度（gradient）的线性组合里每个向量的系数。此方法的证明牵涉到偏微分，全微分或链法，从而找到能让设出的隐函数的微分为零的未知数的值。

引入问题

给定一个函数：$z = f(x, y)$如何求其极值点呢 ？
显然根据多元函数求极值定理(必要条件)：设函数$z = f(x, y)$在点$(x_{0}, y_{0})$具有偏导数，且在点$(x_{0}, y_{0})$处有极值，则有
$f_{x}(x_{0}, y_{0})$ = 0, $f_{y}(x_{0}, y_{0})$ = 0
即：函数在点$(x_{0}, y_{0})$处有偏导且有极值则该点处偏导为0，具体方法不作叙述，参考高等数学Ⅱ
现在将问题难度加大，如果再加上约束条件呢？面积固定，求体积最大？

$V(x,y,z) = xyz$ $2xy+2xz+2yz = S$

---

正文

上图是对拉格朗日乘数法的叙述
假设有两个函数$f(x,y)$和$g(x,y)$，且这两个函数的一阶偏导数都是连续函数，在$g(x,y)=k$   and $\triangledown g(a,b)≠(0,0)$的前提下，函数$f(x,y)$在某个$(a,b)$点产生了局部极值,可以找到一个实数$\lambda$使得$\triangledown f(a,b)=\lambda \triangledown g(a,b)$

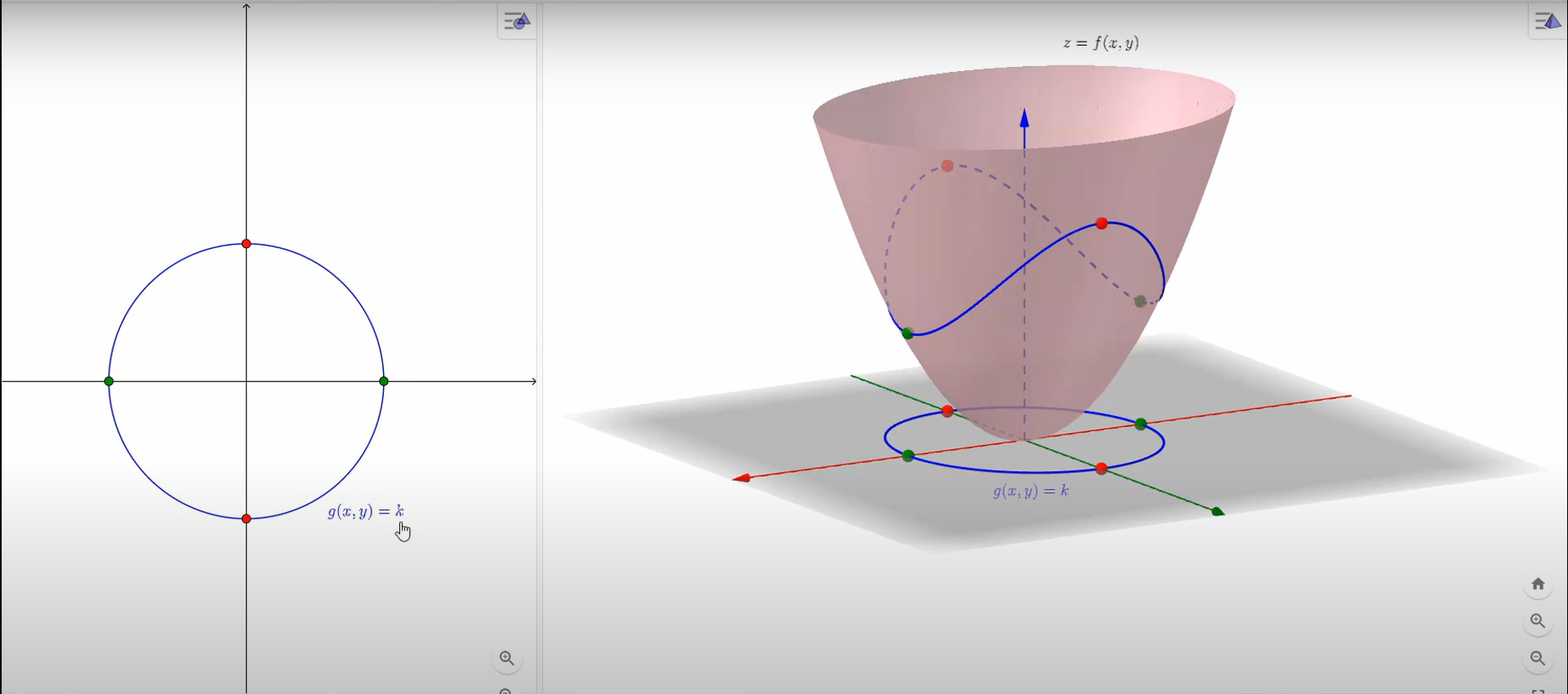
$f(x,y)$是右图中的3D曲面（横截面为椭圆的抛物面），左图中的$g(x,y)$是约束条件,我们将$g(x,y)$向上面的$f(x,y)$进行投影可以得到曲面上有一条蓝色的曲线，这条曲线就是在$g(x,y)$的约束条件下$f(x,y)$的所有取值点，接下来我们就要从中找到最值。

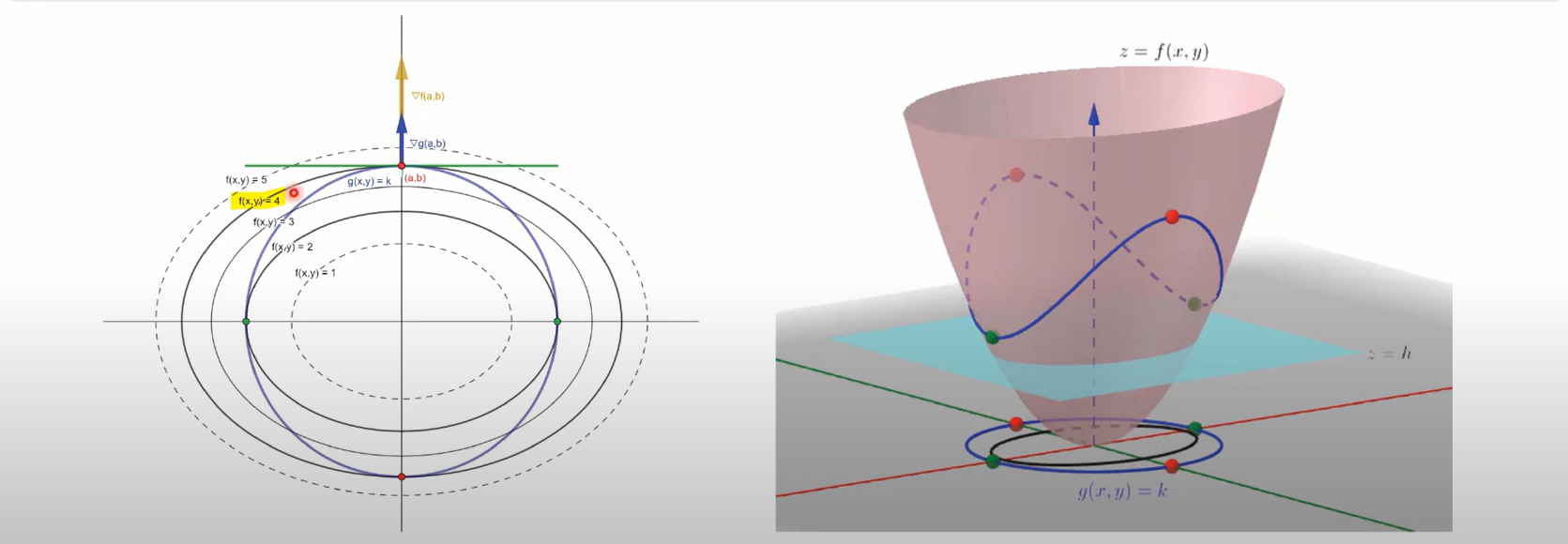
我们引入一个水平面$z=h$,水平面与曲面相交处的投影是一个椭圆，水平面向上移动时，会首先与曲面上蓝色的曲线相交于图上两个绿色的点，此时如左图（投影图）所示，$h=2$。水平面继续向上移动时会与曲面上蓝色的曲线一直相交于4个点，直到相交于两个点时，即为图上的红点，此时如左图所示，$h=4$。当水平面继续向上移动时就再也不可能与曲面上蓝色的曲线相交了。如右图我们可以知道$h=2$和$h=4$时的交点是在约束条件下曲面的极值点，并且此时的蓝色曲线与水平面相切。在左图中可以看出当处于极值点时$f(x,y)$和$g(x,y)$共同相切与同一条直线，所以此时两函数在此交点的处的法向量是共线的，即$\triangledown f(x,y)=\lambda \triangledown g(x,y)$

---

Ep: Find the extreme values of the function $f(x,y)=x^{2}+2y^{2}$ on the circle $x^{2}+y^{2}=1\longrightarrow type1$

Sol: Let $g(x,y)=x^{2}+y^{2}$ and we get circle $\Rightarrow$ $g(x,y)=x^{2}+y^{2}=1$

  If $\triangledown f(x,y)=\lambda \triangledown g(x,y)$, then $(f_{x},f_{y})=\lambda (g_{x},g_{y}) \Rightarrow (2x,4y)=\lambda (2x,2y)$

  $\begin{cases}2x=2\lambda x\Rightarrow& 2x(\lambda-1)=0\Rightarrow x=0,\lambda=1\\4y=2\lambda y\Rightarrow & 2y=\lambda y\longrightarrow type2\end{cases}$

  If x=0, then $type1 \Rightarrow y^{2}=1 \Rightarrow y=±1\Rightarrow(x,y)=(0,1)or(0,-1)$

  If $\lambda$=1, then $type2 \Rightarrow2y=y\Rightarrow y=0\Rightarrow x^{2}=1\Rightarrow x=±1 \\\Rightarrow(x,y)=(1,0)or(-1,0)$

(x,y)	(0,1),(0,-1)	(1,0),(-1,0)
f(x,y)	2,2	1, 1
extremum	abs max value	abs min value

$$f(x,y)\:has\begin{cases}an\:abs\:max\:value\:2\:of\:(0,1),(0,-1)\\an\:abs\:min\:value\:1\:of\:(1,0),(-1,0)\end{cases}$$

简言之

求解函数：$z=f(x,y)$在条件$\phi(x,y)=0$条件下的极值。

解：

1. 构造函数$F(x,y)=f(x,y)+\lambda\phi(x,y)$,其中$\lambda$为拉格朗日乘数

$$\begin{cases}f_{x}(x,y)+\lambda\phi_{x}(x,y)=0 \\f_{y}(x,y)+\lambda\phi_{y}(x,y)=0,\\\phi(x,y)=0.\end{cases}$$

2. 其中$(x,y)$就是极值点坐标

自变量多于两个的条件下

函数：$u=f(x,y,z,t)$在条件$\phi(x,y,z,t)=0, \Psi(x,y,z,t)=0$下的极值

构造函数：$F(x,y,z,t)=f(x,y,z,t)+\lambda_{1}\phi(x,y,z,t)+\lambda_{2}\Psi(x,y,z,t)$

其中$\lambda_{1},\lambda_{2}$均为拉格朗日乘数，同样通过偏导为0以及约束条件求解

如：

函数：$u=x^{3}y^{2}z$，约束条件：$x,y,z$之和为12，求其最大值。

解：

1. 构造函数：$F(x,y,z)=x^{3}y^{2}z+\lambda(x+y+z-12)$

2. 分别求偏导：

$$\begin{cases}F^{’}_{x}=3x^{2}y^{2}z+\lambda=0\\F^{’}_{y}=2x^{3}yz+\lambda=0\\F^{’}_{z}=x^{3}y^{2}+\lambda=0\\x+y+z=12\end{cases}$$

3. 唯一驻点：(6,4,2)

4. $u_{max}=6^{3}\cdot 4^{2}\cdot 2=6912$

例：

在第一卦限内作椭圆球面$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1$的切平面，使切平面与三个坐标面所围成的四面体体积最小，求切点坐标。

解：

设$P(x_{0},y_{0},z_{0})$为椭球面上的一点，令$F(x,y,z)=\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}-1$

则$F^{'}_{x}|_{p}=\frac{2x_{0}}{a^{2}},F^{'}_{y}|_{p}=\frac{2y_{0}}{b^{2}},F^{'}_{z}|_{p}=\frac{2z_{0}}{a^{2}}$

过$P(x_{0},y_{0},z_{0})$的切平面方程为
$\frac{x_{0}}{a^{2}}(x-x_{0})+\frac{y_{0}}{b^{2}}(y-y_{0})+\frac{z_{0}}{c^{2}}(z-z_{0})=0$

化简为$\frac{x·x_{0}}{a^{2}}+\frac{y·y_{0}}{b^{2}}+\frac{z·z_{0}}{c^{2}}=1$

该切平面在三个轴上的截距各为$x=\frac{a^{2}}{x_{0}},y=\frac{b^{2}}{y_{0}},z=\frac{c^{2}}{z_{0}}$

所求四面体的体积$V=\frac{1}{6}xyz=\frac{a^{2}b^{2}c^{2}}{6x_{0}y_{0}z_{0}}$

在条件$\frac{x_{0}^{2}}{a^{2}}+\frac{y_{0}^{2}}{b^{2}}+\frac{z_{0}^{2}}{c^{2}}=1$下求V的最小值，

目标函数$V=\frac{a^{2}b^{2}c^{2}}{6x_{0}y_{0}z_{0}}$, 约束条件$\frac{x_{0}^{2}}{a^{2}}+\frac{y_{0}^{2}}{b^{2}}+\frac{z_{0}^{2}}{c^{2}}=1$

令$u=lnx_{0}+lny_{0}+lnz_{0}$

$L(x_{0},y_{0},z_{0})=lnx_{0}+lny_{0}+lnz_{0}+\lambda(\frac{x_{0}^{2}}{a^{2}}+\frac{y_{0}^{2}}{b^{2}}+\frac{z_{0}^{2}}{c^{2}}-1)$

由$\begin{cases}L^{'}_{x_{0}}=0,L^{'}_{y_{0}}=0,L^{'}_{z_{0}}=0\\\frac{x_{0}^{2}}{a^{2}}+\frac{y_{0}^{2}}{b^{2}}+\frac{z_{0}^{2}}{c^{2}}-1=0\end{cases}$
$L(x_{0},y_{0},z_{0})=lnx_{0}+lny_{0}+lnz_{0}+\lambda(\frac{x_{0}^{2}}{a^{2}}+\frac{y_{0}^{2}}{b^{2}}+\frac{z_{0}^{2}}{c^{2}}-1)$

即$\begin{cases}\frac{1}{x_{0}}+\frac{2\lambda x_{0}}{a^{2}}=0\\\frac{1}{y_{0}}+\frac{2\lambda y_{0}}{b^{2}}=0\\\frac{1}{z_{0}}+\frac{2\lambda z_{0}}{c^{2}}=0\\\frac{x_{0}^{2}}{a^{2}}+\frac{y_{0}^{2}}{b^{2}}+\frac{z_{0}^{2}}{c^{2}}-1=0\end{cases}$, 可得$\begin{cases}x_{0}=\frac{a}{\sqrt{3}}\\y_{0}=\frac{b}{\sqrt{3}}\\z_{0}=\frac{c}{\sqrt{3}}\end{cases}$

故当切点坐标为$(\frac{a}{\sqrt{3}},\frac{b}{\sqrt{3}},\frac{c}{\sqrt{3}})$
四面体的体积最小$V_{min}=\frac{\sqrt{3}}{2}abc$

---

拉格朗日对偶(Lagrange duality)问题

利用拉格朗日对偶性，可以将约束最优化的原始问题(广义拉格朗日极小极大问题)，转变为无约束最优化的对偶问题(拉格朗日极大极小问题)。

原始问题

假设在$x\in R^{n}$下，$f(x),c_{i}(x),h_{j}(x)$连续且可微，约束最优化问题，如下

$$\min \limits_{x\in R^{n}}f(x)\\ s.t\:c_{i}(x)\leqslant0,\:i=1,2,...,k\\ h_{j}(x)=0,\:j=1,2,...,l$$

称为约束最优化问题的原始问题。

引入广义拉格朗日函数(generalized Lagrange function)
$L(x,\alpha,\beta)=f(x)+\displaystyle\sum\limits_{i=1}^k \alpha_{i}c_{i}(x)+\displaystyle\sum\limits_{j=1}^l \beta_{j}h_{j}(x)$
$x=(x^{(1)},x^{(2)},x^{(3)}...x^{(n)})^{T}\in R^{n}$
特别的$\alpha_{i}\geqslant0$

定义$\theta_{p}(x)=\max \limits_{\alpha,\beta:\alpha_{i}\geqslant0}L(x,\alpha,\beta)$

若$x$违背原始的约束条件，$c_{i}(x)>0$则让$\alpha_{i}$为$+\infty$，其他$\alpha和\beta$参数都为0，则$\theta_{p}(x)=+\infty$

若$x$违背原始的约束条件，$h_{i}(x)≠0$则让$\beta_{i}h_{i}(x)=+\infty$，其他$\alpha和\beta$参数都为0，则$\theta_{p}(x)=+\infty$

若$x$满足原始的约束条件，则让全部的$\beta_{i}h_{i}(x)=0和\alpha_{i}c_{i}(x)=0，f(x)$是一个与$\alpha和\beta$无关的常量，则$\theta_{p}(x)=f(x)$，也就是$\theta_{p}(x)=\begin{cases}f(x)，x满足原始问题约束\\+\infty，x不满足原始问题约束\end{cases}$
则原问题(满足约束条件下)等价于：$\min \limits_{x}\theta_{p}(x)=\min \limits_{x}\max \limits_{\alpha,\beta:\alpha_{i}\geqslant0}L(x,\alpha,\beta)=\min \limits_{x}f(x)$

即$\min \limits_{x}\theta_{p}(x)$与原始优化问题等价,所以常用$\min \limits_{x}\theta_{p}(x)$代表原始问题，下标 $P$ 表示原始问题，定义原始问题的最优值为：$p^{*}=\min \limits_{x}\theta_{p}(x)$

通过拉格朗日函数重新定义一个无约束的问题，这个无约束的问题等价于原来的约束优化问题，从而将约束问题无约束化。

对偶问题：

$\theta_{d}(\alpha,\beta)=\min \limits_{x}L(x,\alpha,\beta)$
这里注意等式右边是关于$x$的函数的最小化，$x$确定以后，最小值就只与$\alpha,\beta$有关，所以是一个关于$\alpha,\beta$的函数。

$\max \limits_{\alpha,\beta:\alpha_{i}\geqslant0}\theta_{d}(\alpha,\beta)=\max \limits_{\alpha,\beta:\alpha_{i}\geqslant0}\min \limits_{x}L(x,\alpha,\beta)$

这就是原始问题的对偶问题，再把原始问题写出来：
$\min \limits_{x}\theta_{p}(x)=\min \limits_{x}\max \limits_{\alpha,\beta:\alpha_{i}\geqslant0}L(x,\alpha,\beta)$
形式上可以看出很对称，只不过原始问题是先固定$L(x,\alpha,\beta)$中的$x$，优化出参数$\alpha,\beta$，再优化最优$x$;
而对偶问题是先固定$\alpha,\beta$ ，优化出最优$x$，然后再确定参数$\alpha,\beta$
定义对偶问题的最优值：$d^{*}=\max \limits_{\alpha,\beta:\alpha_{i}\geqslant0}\theta_{d}(\alpha,\beta)$

也就是说原始问题的最优值不小于对偶问题的最优值，但是我们要通过对偶问题来求解原始问题，就必须使得原始问题的最优值与对偶问题的最优值相等，当原始问题与对偶问题的最优值相等时，原始问题和对偶问题的可行解就是最优解。

原始问题与对偶问题的关系

由上述推导有：
$\max \limits_{\alpha,\beta:\alpha_{i}\geqslant0}\theta_{d}(\alpha,\beta)\leqslant\min \limits_{x}\theta_{p}(x)$
即：$d^{*}\leqslant p^{*}$

得出推论：
设$x^{*}和\alpha^{*},\beta^{*}$分别是原始问题和对偶问题的可行解，如果$d^{*}=p^{*}$，则$x^{*}和\alpha^{*},\beta^{*}$分别是原始问题和对偶问题的最优解。

所以，当原始问题和对偶问题的最优值相等：$d^{*}=p^{*}$时，可以用求解对偶问题来求解原始问题（当然是对偶问题求解比直接求解原始问题简单的情况下），满足什么样的条件才能使原始问题的最优值与对偶问题的最优值相等，KKT条件：

$$\nabla_{x}L(x,\alpha,\beta)=0\\ \nabla_{\alpha}L(x,\alpha,\beta)=0\\ \nabla_{\beta}L(x,\alpha,\beta)=0\\ \alpha_{i}c_{i}(x)=0,\:i=1,2,...,k\\ c_{i}(x)\leqslant0,\:i=1,2,...,k\\ \alpha_{i}\geqslant0,\:i=1,2,...,k\\ h_{j}(x)=0,\:j=1,2,...,l$$

前面三个条件对应各个变量的偏导数为0（这里需要假设三个函数连续可微，若不连续，这里的偏导数存在与否就不能够保证），后面四个条件就是原始问题的约束条件以及拉格朗日乘子需要满足的约束，其中$\alpha_{i}c_{i}=0$为对偶互补条件。