日常学习随笔-用链表的形式实现普通二叉树的删除(源码+说明)(补充篇)
一、二叉树删除的三种情况
删除二叉树查找树的节点吧。总共有三种情况
1.被删除的节点是叶子节点,这时候只要把这个节点删除,再把指向这个节点的父节点指针置为空就行
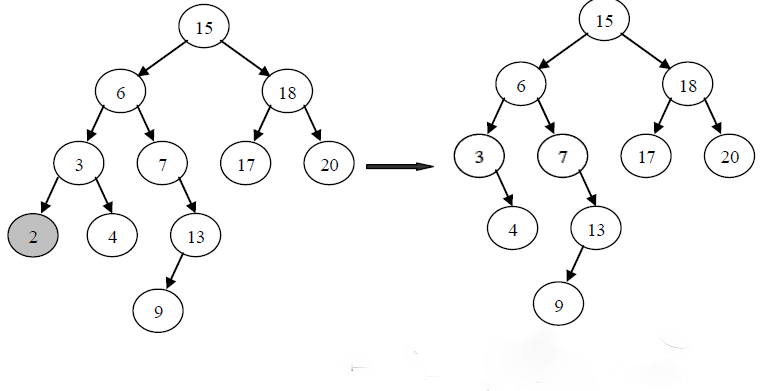
2.被删除的节点有左子树,或者有右子树,而且只有其中一个,那么只要把当前删除节点的父节点指向被删除节点的左子树或者右子树就行。
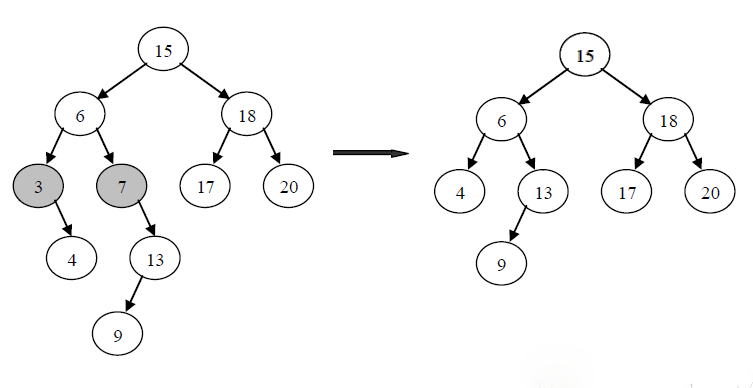
3.被删除的节点既有左子树而且又有右子树,这时候需要把左子树的最右边的节点或者右子树最左边的节点提到被删除节点的位置,为什么要这样呢,根据二叉查找树的性质,父节点的指针一定比所有左子树的节点值大而且比右子树的节点的值小,为了删除父节点不破坏二叉查找树的平衡性,应当把左子树最大的节点或者右子树最小的节点放在父节点的位置,这样的话才能维护二叉查找树的平衡性。(我是找的左子树的最大节点)
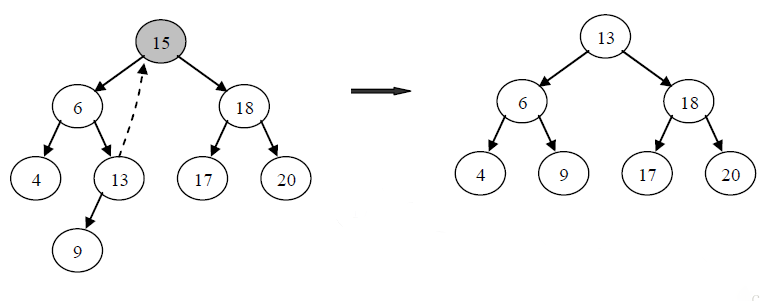
或者
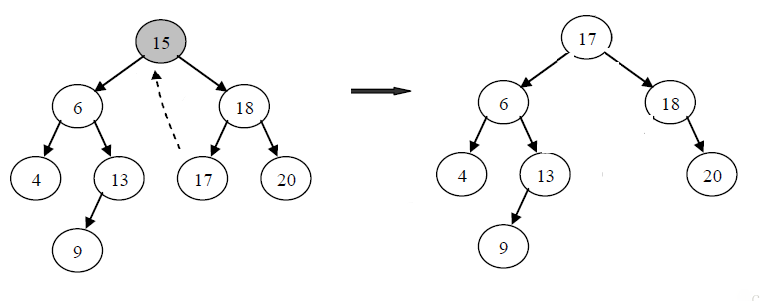
二、源码案例:
完整的二叉树类:

二叉树完整自定义源码:

1 package com.xfwl.algorithmAnalysis.trees; 2 /** 3 * 二叉树结构分析 4 * @function 日常学习测试 5 * @author 小风微凉 6 * @time 2018-5-20 下午12:28:50 7 */ 8 public class MyTreeDefin<T extends Comparable<? super T>>{ 9 /** 10 * 每棵树都有一个根节点 11 */ 12 private BinaryNode<T> root; 13 /** 14 * 整棵树的节点个数 15 */ 16 private int nodeCount; 17 /** 18 * 二叉树构造器 19 */ 20 public MyTreeDefin(){ 21 this.reset(); 22 } 23 /** 24 * 重置整棵树的结构 25 */ 26 private void reset(){ 27 //二叉树的根节点初始化 28 root=null; 29 //二叉树的节点总数:归0 30 this.nodeCount=0; 31 } 32 /** 33 * 清空整棵二叉树 34 * @return 35 */ 36 public boolean makeEmpty(){ 37 this.reset(); 38 return this.isEmpty(); 39 } 40 /** 41 * 获取树的节点个数 42 * @return 43 */ 44 public int getSize(){ 45 return this.nodeCount; 46 } 47 /** 48 * 判断整棵树是否为空树 49 * @return 50 */ 51 public boolean isEmpty(){ 52 return this.nodeCount==0?true:false; 53 } 54 /** 55 * 判断二叉树中指定节点后面是否包含指定数据 56 * @param target 检索数据target 57 * @param node 指定的节点(包含当前节点) 58 * @return 59 */ 60 public boolean contains(T target,BinaryNode<T> node){ 61 //判空检查 62 if(node==null){ 63 return false; 64 } 65 //先和当前节点的数据比较 66 int compareResult=target.compareTo(node.elem); 67 if(compareResult>0){//进入右子树中继续判断 68 return contains(target,node.right); 69 }else if(compareResult<0){//进入左子树中继续判断 70 return contains(target,node.left); 71 }else{//相等 72 return true; 73 } 74 } 75 /** 76 * 从根节点开始查找整棵树是否包含指定的数据 77 * @param target 检索数据target 78 * @return 79 */ 80 public boolean contains(T target){ 81 return this.contains(target, this.root); 82 } 83 /** 84 * 查找整棵树中的最小数据 85 * 左子树最后一个节点数据 86 * @return 87 */ 88 public T findMin(){ 89 return this.findMin(this.root).elem; 90 } 91 /** 92 * 查找指定树节点下面的最小节点[查找指定节点后面的最小节点] 93 * @param node 指定的节点 94 * @return 95 */ 96 public BinaryNode<T> findMin(BinaryNode<T> node){ 97 //如果节点为空 98 if(node==null){ 99 return null; 100 }else if(node.left==null){//递归基准情况 101 return node; 102 }else{//递归流程 103 return findMin(node.left); 104 } 105 } 106 /** 107 * 查找指定树节点下面的最大节点[最大的数据在右子树的最深叶子节点] 108 * @param node 指定的查找起点节点 109 * @return 110 */ 111 public BinaryNode<T> findMax(BinaryNode<T> node){ 112 //如果节点为空 113 if(node==null){ 114 return null; 115 }else if(node.right==null){//递归基准情况 116 return node; 117 }else{//递归流程 118 return findMax(node.right); 119 } 120 } 121 /** 122 * 查找整棵树中的最大数据 123 * @return 124 */ 125 public T findMax(){ 126 return this.findMax(this.root).elem; 127 } 128 /** 129 * 为二叉树添加新的节点(对外) 130 * @param data 要添加的数据 131 * @return 132 */ 133 public BinaryNode<T> add(T data){ 134 if(this.isEmpty()){ 135 this.nodeCount++; 136 this.root=new BinaryNode<>(data,null,null); 137 return this.root; 138 }else{ 139 this.nodeCount++; 140 return this.add(data, this.root); 141 } 142 } 143 /** 144 * 为二叉树添加新的节点(对内) 145 * @param data 要添加的数据 146 * @param curNode 要添加的节点(递归比较) 147 */ 148 private BinaryNode<T> add(T data,BinaryNode<T> curNode){ 149 //如果节点不存在:递归基准情况 150 if(curNode==null){ 151 return new BinaryNode<>(data,null,null); 152 } 153 //按照:左>根>右 的大小顺序插入二叉树中 154 //比较起点:先和根节点数据比较 155 int compareResult=data.compareTo(curNode.elem); 156 if(compareResult<0){//走左子树 157 System.out.println("左<--"); 158 curNode.left=this.add(data,curNode.left); 159 }else if(compareResult>0){//走右子树 160 System.out.println("-->右"); 161 curNode.right=this.add(data,curNode.right); 162 }else{//如果添加的节点数据和当前比较的根节点相同 163 //不做任何处理,可在此继续扩展 164 } 165 //返回的是根节点 166 return curNode; 167 } 168 /** 169 * 非递归添加树节点 170 * @param data 节点数据 171 * @return 172 */ 173 public void push(T data){ 174 if(this.isEmpty()){//空树结构 175 this.nodeCount++; 176 this.root=new BinaryNode<>(data,null,null); 177 }else{//至少含有一个根节点 178 BinaryNode<T> tmpNode =this.root; 179 System.out.println("--------------------根节点数据:"+tmpNode.elem+",--------------------"); 180 while(true){ 181 System.out.println("while----:tmpNode.elem="+tmpNode.elem+",data="+data); 182 int compareResult=data.compareTo(tmpNode.elem); 183 if(compareResult<0){//走左子树 184 System.out.println("左<--"); 185 if(tmpNode.left==null){ 186 tmpNode.left=new BinaryNode<>(data,null,null); 187 break; 188 } 189 tmpNode=tmpNode.left; 190 }else if(compareResult>0){//走右子树 191 System.out.println("-->右"); 192 if(tmpNode.right==null){ 193 tmpNode.right=new BinaryNode<>(data,null,null); 194 break; 195 } 196 tmpNode=tmpNode.right; 197 }else{//替换当前节点数据(压入相同数据,没改变) 198 //也即不做处理 199 break; 200 } 201 } 202 this.nodeCount++; 203 } 204 } 205 /** 206 * 移除二叉树中根节点后面的指定数据(所在的节点) 207 * @param data 指定的数据 208 */ 209 public boolean remove(T data){ 210 boolean ret=false; 211 //要删除的数据所在的结点存在 212 if(!this.contains(data)){ 213 return ret; 214 } 215 //要删除的节点 216 BinaryNode<T> target=this.getNode(data, this.root); 217 if(target!=null){ 218 //要删除的节点的上一级节点 219 BinaryNode<T> parNode= this.getPrevNode(data); 220 System.out.println("parNode==null:"+(parNode==null)); 221 //(1)当前节点为叶子节点 222 if(target.left==null && target.right==null){ 223 target=null; 224 if(parNode!=null){ 225 if(data.compareTo(parNode.elem)>0){//右子树 226 parNode.right=null; 227 }else if(data.compareTo(parNode.elem)<0){//左子树 228 parNode.left=null; 229 } 230 }else{//删除的是根节点 231 this.root=null; 232 } 233 ret=true; 234 } 235 //(2)只有一个子树(左或者右) 236 else if(target.left!=null && target.right==null){ 237 target=target.left; 238 if(parNode!=null){ 239 if(data.compareTo(parNode.elem)>0){//右子树 240 parNode.right=target; 241 }else if(data.compareTo(parNode.elem)<0){//左子树 242 parNode.left=target; 243 } 244 }else{//删除的是根节点 245 this.root=this.root.left; 246 } 247 ret=true; 248 }else if(target.left==null && target.right!=null){ 249 target=target.right; 250 if(parNode!=null){ 251 if(data.compareTo(parNode.elem)>0){//右子树 252 parNode.right=target; 253 }else if(data.compareTo(parNode.elem)<0){//左子树 254 parNode.left=target; 255 } 256 }else{//删除的是根节点 257 this.root=this.root.right; 258 } 259 ret=true; 260 } 261 //(3)左右子树都有 262 /** 263 * 最麻烦的一种删除方式: 264 * [1]找到要删除节点的父节点,判断当前节点是在父节点的左子树还是右子树。 265 * [2]找到当前删除节点的左子树的最大节点,替换当前删除节点。 266 * [3]当前删除节点的左子树的最大节点的父节点(针对这个节点的指向清空) 267 * [4]重新设置新结点的左右子树的指向 268 */ 269 else if(target.left!=null && target.right!=null){ 270 //1.取左子树的最大数据节点 271 BinaryNode<T> lmaxNode=this.findMax(target.left); 272 if(parNode!=null){//删除的非根节点 273 if(data.compareTo(parNode.elem)>0){//右子树 274 //2.左子树最大数据节点的上级节点 275 BinaryNode<T> maxParNode=this.getPrevNode(lmaxNode.getElem()); 276 if(lmaxNode.getElem().compareTo(maxParNode.elem)>0){ 277 if(lmaxNode.left!=null){ 278 maxParNode.right=lmaxNode.left; 279 }else{ 280 maxParNode.right=null; 281 } 282 }else if(lmaxNode.getElem().compareTo(maxParNode.elem)<0){ 283 //特别注意:当maxParNode的上一级就是target的时候,需要特殊处理 284 if(maxParNode.elem.equals(target.elem)){ 285 maxParNode.left=lmaxNode.left; 286 }else{ 287 maxParNode.left=null; 288 } 289 } 290 //3.替换当前删除节点 291 lmaxNode.left=target.left; 292 lmaxNode.right=target.right; 293 parNode.right=lmaxNode; 294 }else if(data.compareTo(parNode.elem)<0){//左子树 295 //2.左子树最大数据节点的上级节点 296 BinaryNode<T> maxParNode=this.getPrevNode(lmaxNode.getElem()); 297 if(lmaxNode.getElem().compareTo(maxParNode.elem)>0){ 298 if(lmaxNode.left!=null){ 299 maxParNode.right=lmaxNode.left; 300 }else{ 301 maxParNode.right=null; 302 } 303 }else if(lmaxNode.getElem().compareTo(maxParNode.elem)<0){ 304 //特别注意:当maxParNode的上一级就是target的时候,需要特殊处理 305 if(maxParNode.elem.equals(target.elem)){ 306 maxParNode.left=lmaxNode.left; 307 }else{ 308 maxParNode.left=null; 309 } 310 } 311 //3.替换当前删除节点 312 lmaxNode.left=target.left; 313 lmaxNode.right=target.right; 314 parNode.left=lmaxNode; 315 } 316 }else{//删除的是根节点 317 //2.左子树最大数据节点的上级节点 318 BinaryNode<T> maxParNode=this.getPrevNode(lmaxNode.getElem()); 319 if(lmaxNode.getElem().compareTo(maxParNode.elem)>0){ 320 if(lmaxNode.left!=null){ 321 maxParNode.right=lmaxNode.left; 322 }else{ 323 maxParNode.right=null; 324 } 325 }else if(lmaxNode.getElem().compareTo(maxParNode.elem)<0){ 326 //特别注意:当maxParNode的上一级就是target的时候,需要特殊处理 327 if(maxParNode.elem.equals(target.elem)){ 328 maxParNode.left=lmaxNode.left; 329 }else{ 330 maxParNode.left=null; 331 } 332 } 333 //3.替换当前删除节点 334 lmaxNode.left=target.left; 335 lmaxNode.right=target.right; 336 this.root=lmaxNode; 337 } 338 ret=true; 339 } 340 } 341 this.nodeCount=(ret==true?--this.nodeCount:this.nodeCount); 342 //找到要删除的节点 343 return ret; 344 } 345 public T getPrevNodeElem(T data){ 346 return this.getPrevNode(data).getElem(); 347 } 348 /** 349 * 根据节点数据找到对应的节点的父节点 350 * @param data 节点数据 351 * @return 352 */ 353 public BinaryNode<T> getPrevNode(T data){ 354 if(this.isEmpty()){//空树 355 return null; 356 } 357 if(data.equals(root.getElem())){ 358 return null; 359 } 360 BinaryNode<T> parNode=this.root;//父节点 361 BinaryNode<T> curNode=this.root;//当前节点 362 while(true){ 363 int compareResult=data.compareTo(curNode.elem); 364 if(compareResult>0){//进入右子树中继续判断 365 /*parNode.elem=curNode.elem; 366 parNode.left=curNode.left; 367 parNode.right=curNode.right;*/ 368 parNode=curNode; 369 curNode=curNode.right; 370 }else if(compareResult<0){//进入左子树中继续判断 371 /*parNode.elem=curNode.elem; 372 parNode.left=curNode.left; 373 parNode.right=curNode.right;*/ 374 parNode=curNode; 375 376 curNode=curNode.left; 377 }else{//相等 378 break; 379 } 380 } 381 return parNode; 382 } 383 /** 384 * 根据节点数据找到对应的节点 385 * @param data 节点数据 386 * @param node 387 * @return 388 */ 389 public BinaryNode<T> getNode(T data,BinaryNode<T> node){ 390 //不存在节点 391 if(this.isEmpty()){ 392 return null; 393 } 394 //先和当前节点的数据比较 395 int compareResult=data.compareTo(node.elem); 396 if(compareResult>0){//进入右子树中继续判断 397 return getNode(data,node.right); 398 }else if(compareResult<0){//进入左子树中继续判断 399 return getNode(data,node.left); 400 }else{//相等 401 return node; 402 } 403 } 404 /** 405 * 打印树结构信息 406 * @param index 遍历的类型 407 * 一般用到的遍历方式有三种: 408 * (1)前序遍历 0 409 * (2)中序遍历 1 410 * (3)后序遍历 2 411 */ 412 public void printTree(int index){ 413 String type=(index==0?"前序":index==1?"中序":"后序")+"遍历"; 414 System.out.println("------------【开始遍历打印·"+type+"】------------"); 415 switch(index){ 416 case 0:preOrder(this.root);break; 417 case 1:inOrder(this.root);break; 418 case 2:postOrder(this.root);break; 419 } 420 System.out.println("------------【打印结束】------------"); 421 } 422 /** 423 * 前序遍历 424 * @param node 遍历的起始节点 425 * 采用递归思想 426 * 对左子节点进行遍历 427 * 对右子节点进行遍历 428 * 递归基值是node是否是null 429 */ 430 private void preOrder(BinaryNode<T> node) 431 { 432 if(node==null){ 433 return; 434 }else{ 435 System.out.print(node.elem+" ");//输出数据节点信息 436 preOrder(node.left); 437 preOrder(node.right); 438 } 439 } 440 /** 441 * 中序遍历 442 * @param node 443 */ 444 private void inOrder(BinaryNode<T> node){ 445 if(node==null){ 446 return; 447 }else{ 448 inOrder(node.left); 449 System.out.print(node.elem+" "); 450 inOrder(node.right); 451 } 452 } 453 /** 454 * 后序遍历 455 * @param node 456 */ 457 private void postOrder(BinaryNode<T> node){ 458 if(node==null){ 459 return; 460 }else{ 461 postOrder(node.left); 462 postOrder(node.right); 463 System.out.print(node.elem+" "); 464 } 465 } 466 /** 467 * 获取指定节点的数据 468 * @param node 469 * @return 470 */ 471 public T getElem(BinaryNode<T> node){ 472 if(node==null){ 473 return null; 474 } 475 return node.elem; 476 } 477 /** 478 * 内置一个树节点类 479 */ 480 private static class BinaryNode<T>{ 481 /** 482 * 树节点存放数据域 483 */ 484 T elem; 485 /** 486 * 左子树节点域 487 */ 488 BinaryNode<T> left; 489 /** 490 * 右子树节点域 491 */ 492 BinaryNode<T> right; 493 /** 494 * 构造器 495 */ 496 public BinaryNode(T elem,BinaryNode<T> left,BinaryNode<T> right){ 497 this.elem=elem; 498 this.left=left; 499 this.right=right; 500 } 501 public T getElem(){ 502 return this.elem; 503 } 504 } 505 } 506
删除功能的代码如下:
(1)根据数据找到二叉树中的结点
1 /** 2 * 根据节点数据找到对应的节点 3 * @param data 节点数据 4 * @param node 5 * @return 6 */ 7 public BinaryNode<T> getNode(T data,BinaryNode<T> node){ 8 //不存在节点 9 if(this.isEmpty()){ 10 return null; 11 } 12 //先和当前节点的数据比较 13 int compareResult=data.compareTo(node.elem); 14 if(compareResult>0){//进入右子树中继续判断 15 return getNode(data,node.right); 16 }else if(compareResult<0){//进入左子树中继续判断 17 return getNode(data,node.left); 18 }else{//相等 19 return node; 20 } 21 }
(2)查找删除数据的上一级节点
1 /** 2 * 根据节点数据找到对应的节点的父节点 3 * @param data 节点数据 4 * @return 5 */ 6 public BinaryNode<T> getPrevNode(T data){ 7 if(this.isEmpty()){//空树 8 return null; 9 } 10 if(data.equals(root.getElem())){ 11 return null; 12 } 13 BinaryNode<T> parNode=this.root;//父节点 14 BinaryNode<T> curNode=this.root;//当前节点 15 while(true){ 16 int compareResult=data.compareTo(curNode.elem); 17 if(compareResult>0){//进入右子树中继续判断 18 /*parNode.elem=curNode.elem; 19 parNode.left=curNode.left; 20 parNode.right=curNode.right;*/ 21 parNode=curNode; 22 curNode=curNode.right; 23 }else if(compareResult<0){//进入左子树中继续判断 24 /*parNode.elem=curNode.elem; 25 parNode.left=curNode.left; 26 parNode.right=curNode.right;*/ 27 parNode=curNode; 28 29 curNode=curNode.left; 30 }else{//相等 31 break; 32 } 33 } 34 return parNode; 35 }
(3)判断二叉树是否包含要删除的数据
1 /** 2 * 判断二叉树中指定节点后面是否包含指定数据 3 * @param target 检索数据target 4 * @param node 指定的节点(包含当前节点) 5 * @return 6 */ 7 public boolean contains(T target,BinaryNode<T> node){ 8 //判空检查 9 if(node==null){ 10 return false; 11 } 12 //先和当前节点的数据比较 13 int compareResult=target.compareTo(node.elem); 14 if(compareResult>0){//进入右子树中继续判断 15 return contains(target,node.right); 16 }else if(compareResult<0){//进入左子树中继续判断 17 return contains(target,node.left); 18 }else{//相等 19 return true; 20 } 21 }
(4)查找二叉树指定结点的左子树中最大的节点
1 /** 2 * 查找指定树节点下面的最大节点[最大的数据在右子树的最深叶子节点] 3 * @param node 指定的查找起点节点 4 * @return 5 */ 6 public BinaryNode<T> findMax(BinaryNode<T> node){ 7 //如果节点为空 8 if(node==null){ 9 return null; 10 }else if(node.right==null){//递归基准情况 11 return node; 12 }else{//递归流程 13 return findMax(node.right); 14 } 15 } 16 /** 17 * 查找整棵树中的最大数据 18 * @return 19 */ 20 public T findMax(){ 21 return this.findMax(this.root).elem; 22 }
(5)*删除指定数据所在的节点
1 /** 2 * 移除二叉树中根节点后面的指定数据(所在的节点) 3 * @param data 指定的数据 4 */ 5 public boolean remove(T data){ 6 boolean ret=false; 7 //要删除的数据所在的结点存在 8 if(!this.contains(data)){ 9 return ret; 10 } 11 //要删除的节点 12 BinaryNode<T> target=this.getNode(data, this.root); 13 if(target!=null){ 14 //要删除的节点的上一级节点 15 BinaryNode<T> parNode= this.getPrevNode(data); 16 System.out.println("parNode==null:"+(parNode==null)); 17 //(1)当前节点为叶子节点 18 if(target.left==null && target.right==null){ 19 target=null; 20 if(parNode!=null){ 21 if(data.compareTo(parNode.elem)>0){//右子树 22 parNode.right=null; 23 }else if(data.compareTo(parNode.elem)<0){//左子树 24 parNode.left=null; 25 } 26 }else{//删除的是根节点 27 this.root=null; 28 } 29 ret=true; 30 } 31 //(2)只有一个子树(左或者右) 32 else if(target.left!=null && target.right==null){ 33 target=target.left; 34 if(parNode!=null){ 35 if(data.compareTo(parNode.elem)>0){//右子树 36 parNode.right=target; 37 }else if(data.compareTo(parNode.elem)<0){//左子树 38 parNode.left=target; 39 } 40 }else{//删除的是根节点 41 this.root=this.root.left; 42 } 43 ret=true; 44 }else if(target.left==null && target.right!=null){ 45 target=target.right; 46 if(parNode!=null){ 47 if(data.compareTo(parNode.elem)>0){//右子树 48 parNode.right=target; 49 }else if(data.compareTo(parNode.elem)<0){//左子树 50 parNode.left=target; 51 } 52 }else{//删除的是根节点 53 this.root=this.root.right; 54 } 55 ret=true; 56 } 57 //(3)左右子树都有 58 /** 59 * 最麻烦的一种删除方式: 60 * [1]找到要删除节点的父节点,判断当前节点是在父节点的左子树还是右子树。 61 * [2]找到当前删除节点的左子树的最大节点,替换当前删除节点。 62 * [3]当前删除节点的左子树的最大节点的父节点(针对这个节点的指向清空) 63 * [4]重新设置新结点的左右子树的指向 64 */ 65 else if(target.left!=null && target.right!=null){ 66 //1.取左子树的最大数据节点 67 BinaryNode<T> lmaxNode=this.findMax(target.left); 68 if(parNode!=null){//删除的非根节点 69 if(data.compareTo(parNode.elem)>0){//右子树 70 //2.左子树最大数据节点的上级节点 71 BinaryNode<T> maxParNode=this.getPrevNode(lmaxNode.getElem()); 72 if(lmaxNode.getElem().compareTo(maxParNode.elem)>0){ 73 if(lmaxNode.left!=null){ 74 maxParNode.right=lmaxNode.left; 75 }else{ 76 maxParNode.right=null; 77 } 78 }else if(lmaxNode.getElem().compareTo(maxParNode.elem)<0){ 79 //特别注意:当maxParNode的上一级就是target的时候,需要特殊处理 80 if(maxParNode.elem.equals(target.elem)){ 81 maxParNode.left=lmaxNode.left; 82 }else{ 83 maxParNode.left=null; 84 } 85 } 86 //3.替换当前删除节点 87 lmaxNode.left=target.left; 88 lmaxNode.right=target.right; 89 parNode.right=lmaxNode; 90 }else if(data.compareTo(parNode.elem)<0){//左子树 91 //2.左子树最大数据节点的上级节点 92 BinaryNode<T> maxParNode=this.getPrevNode(lmaxNode.getElem()); 93 if(lmaxNode.getElem().compareTo(maxParNode.elem)>0){ 94 if(lmaxNode.left!=null){ 95 maxParNode.right=lmaxNode.left; 96 }else{ 97 maxParNode.right=null; 98 } 99 }else if(lmaxNode.getElem().compareTo(maxParNode.elem)<0){ 100 //特别注意:当maxParNode的上一级就是target的时候,需要特殊处理 101 if(maxParNode.elem.equals(target.elem)){ 102 maxParNode.left=lmaxNode.left; 103 }else{ 104 maxParNode.left=null; 105 } 106 } 107 //3.替换当前删除节点 108 lmaxNode.left=target.left; 109 lmaxNode.right=target.right; 110 parNode.left=lmaxNode; 111 } 112 }else{//删除的是根节点 113 //2.左子树最大数据节点的上级节点 114 BinaryNode<T> maxParNode=this.getPrevNode(lmaxNode.getElem()); 115 if(lmaxNode.getElem().compareTo(maxParNode.elem)>0){ 116 if(lmaxNode.left!=null){ 117 maxParNode.right=lmaxNode.left; 118 }else{ 119 maxParNode.right=null; 120 } 121 }else if(lmaxNode.getElem().compareTo(maxParNode.elem)<0){ 122 //特别注意:当maxParNode的上一级就是target的时候,需要特殊处理 123 if(maxParNode.elem.equals(target.elem)){ 124 maxParNode.left=lmaxNode.left; 125 }else{ 126 maxParNode.left=null; 127 } 128 } 129 //3.替换当前删除节点 130 lmaxNode.left=target.left; 131 lmaxNode.right=target.right; 132 this.root=lmaxNode; 133 } 134 ret=true; 135 } 136 } 137 this.nodeCount=(ret==true?--this.nodeCount:this.nodeCount); 138 //找到要删除的节点 139 return ret; 140 }
测试类:
1 package com.xfwl.algorithmAnalysis.trees; 2 3 public class Test { 4 /** 5 * @param args 6 */ 7 public static void main(String[] args) { 8 //创建一棵树 9 MyTreeDefin<Integer> tree=new MyTreeDefin<>(); 10 //压入数据 11 tree.push(5); 12 tree.push(2); 13 tree.push(4); 14 tree.push(8); 15 tree.push(7); 16 tree.push(11); 17 tree.push(3); 18 tree.push(9); 19 tree.push(6); 20 tree.push(1); 21 tree.push(0); 22 tree.push(10); 23 System.out.println(tree.getSize()); 24 //开始遍历显示 25 //tree.printTree(0); 26 //tree.printTree(1); 27 //tree.printTree(2); 28 //删除 29 tree.remove(5); 30 tree.printTree(1); 31 //System.out.println(tree.getSize()); 32 33 //System.out.println(tree.getPrevNodeElem(2)); 34 } 35 }
运行结果比较多,就不一一展示在这里了!
研究技术需要静下心来,一点一点地深究.......



 浙公网安备 33010602011771号
浙公网安备 33010602011771号