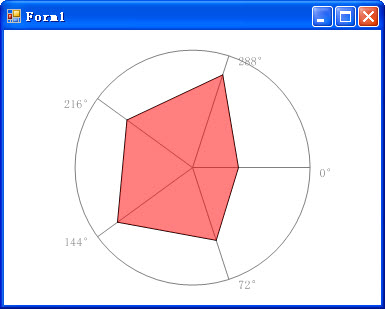
这是一个简单的GDI+的例子。讲的是怎么从无到有绘制一个极坐标系，以及在此基础上绘制数据图。按照类似的思路，你可以画出直角坐标系、对数直角系、外太空银河系……
本文比较浅显，觉得没有帮助者请按组合键：Alt+F4，走好。
欢迎大家指教，欢迎改造，然后把代码和图贴在这里。大家一起看看能把自己的创造力激发到什么程度。
你可以通过本文学到怎么用非数学的方法解决数学问题，以此类推，就算碰到不懂的东西，也可以用自己懂的东西来代替。编程序，尤其是界面编程，只需要「看起来一样」，更敬业点就「用起来一样」。至于你要不要用什么jjyy的技术，的技巧，的手段，都是浮云。
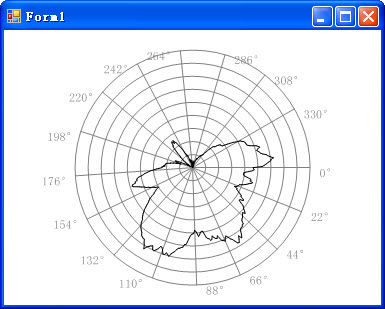
不多说了。我们要做的东西最后效果是这样的。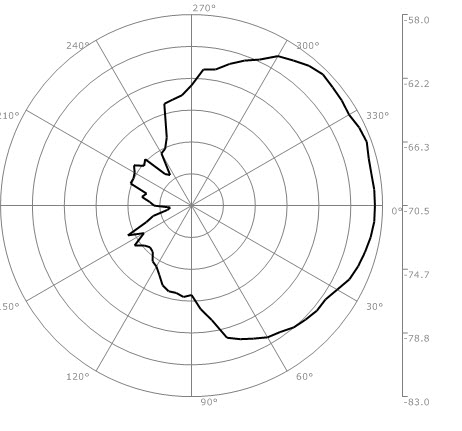
图中曲线是一个天线方向图，非常适合在极坐标下描绘。 文中是直接在窗体上绘制，你完全可以自行封装到控件里，这样用起来更加方便。
（正文开始） 写在前面的话 做事情，一切以目标为出发点，倒着找过去，看有哪些方法技术资源，具体的方法技术手段都是次要的，只要能达到目的。 我不会多线程，如果你需要让它运行在单独的线程上，还请自己改造。（似乎还真有这样ocd的人吧，哈哈）
目标设定 （下面是例子，不针对任何人物、事件、团体、星球） boss接到了一单生意，是帮某山寨厂做一个山寨手机天线的信号测试系统。其中，我分到的部分是做天线方向图的显示界面模块。其实我懂个p的天线、方向图之类的啊，于是boss告诉我，并强调：我不管你怎么做，总之要「看起来」像这样。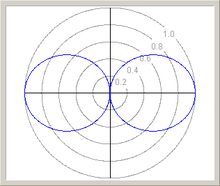
ok，不管会不会，山寨是本行，拿着原版开始分析。
分析坐标系 说实话，数学那套玩意老早就还给老师了，现在要让我玩坐标系这样高深的东西。得亏哥们还有点印象，这样圆不拉叽的图，一般用极坐标来画是比较方便的。连上Wikipedia复习一下：极坐标是一个二维坐标系统。该坐标系统中的点由一个夹角和一段相对中心点——极点（相当于我们较为熟知的直角坐标系中的原点）的距离来表示。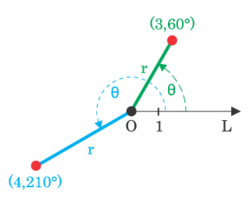
嗯，很好，乱七八糟的，看不太懂啊，怎么办。不管了，把这东西先放一遍，还是用山寨的方法解决。把boss给的那张图拿来分析下，其实就是很多同心圆，和过圆心的辐条（借用自行车术语，虽然不知道正确的名字，就这么叫了吧）。
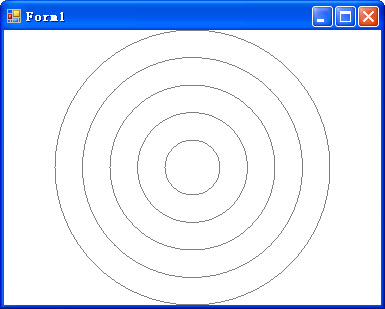
那么我只需要画出同心圆，再画辐条，就ok了吧。画同心圆怎么画呢？嗯，我可以这样，从外面的大圆开始，用DrawEllipse()画一个圆，然后收缩下半径，再画一个，如此这般……好了，有想法就行动，管他是nb方法还是sb方法，一直坐那zb，最后被炒了那才sb。
画出同心圆的方法。
View Code
// 画圆 private void drawCircles(Graphics g, Rectangle rect) { // 圆的直径等于绘图区域最短边 float diameter = Math.Min(rect.Width, rect.Height); // 半径 float radius = diameter / 2; // 计算圆心（其实就是绘图区域矩形中心） PointF center = new PointF( rect.X + rect.Width / 2, rect.Y + rect.Height / 2 ); // 画几个圆，先试试5个 int count = 5; float diameterStep = diameter / count; float radiusStep = radius / count; // 生成圆的范围 RectangleF cirleRect = new RectangleF(); cirleRect.X = center.X - radius; cirleRect.Y = center.Y - radius; cirleRect.Width = cirleRect.Height = diameter; // 画同心圆 for (int i = 0; i < count; i++) { g.DrawEllipse(Pens.Gray, cirleRect); cirleRect.X += radiusStep; cirleRect.Y += radiusStep; cirleRect.Width -= diameterStep; cirleRect.Height -= diameterStep; } }
把这段代码添加到Paint事件里，看看效果如何。
Good，效果还凑合，好像有点锯齿哦，那我就把抗锯齿打开，顺手把文字抗锯齿也打开。
|
1
2
|
e.Graphics.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias; // 图形抗锯齿 e.Graphics.TextRenderingHint = System.Drawing.Text.TextRenderingHint.AntiAlias; // 文字抗锯齿 |
接下来就要画辐条了。那个线可不能就像图里一个十字叉就完事了的，肯定要能自己设n条。想当初就是曾经思维简单了没有考虑到这种变数，被客户和boss烦得天昏地暗。再也不会上当了。
辐条怎么画呢，思考下，在草稿纸上画画先。
（以下都是中学数学，本人上了大学以后数学从没及格过）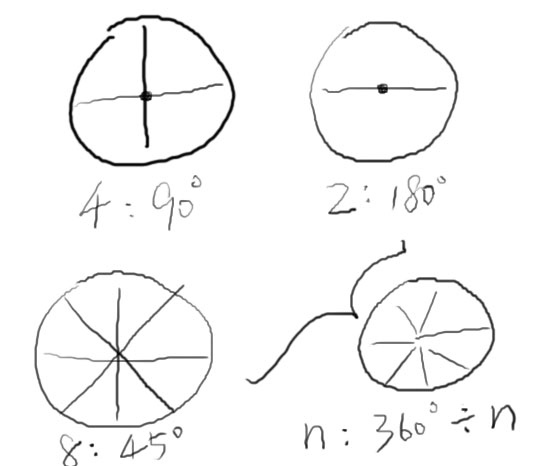
从少到多看看辐条的规律。啊，原来是这样啊，我不一定非要把辐条看成穿过圆心的，我可以看成从圆心发出的n个射线，把圆切成了n个扇面，每个角度就是360°÷n。这样那就好办了，刚才我画圆的时候已经算出来圆心位置了，只要再算出射线终点的坐标，就可以用DrawLine()画线了。但是，射线终点又要怎么算呢，我可是要画到GDI+里哦。
用黑色的笔画出圆，红色的画出GDI+坐标系，那么就可以算出来终点在GDI+下的坐标。圆心(x0,y0)和r半径刚才我已经算出来了，θ就是360/n。现在所有参数都确定了，只要把圆心、半径这几个我需要使用的变量从画圆的方法里拿出来大家用，我就可以开始写画辐条的方法了。
// 提出来公用 float diameter, radius; PointF center; // 画圆 private void drawCircles(Graphics g, Rectangle rect) { // （略） } // 辐射线 private void drawCrosshair(Graphics g) { int count = 8; if (count > 0) { // 计算角度 float angle = 0; float angleStep = 360 / count; PointF endPoint = new PointF(); for (int i = 0; i < count; i++) { // 得到终点 endPoint = getPoint(angle); g.DrawLine(Pens.Gray, center, endPoint); angle += angleStep; angle %= 360; } } } // 计算终点 private PointF getPoint(double angle) { PointF pt = new PointF(); pt.X = (float)(radius * Math.Cos(angle * Math.PI / 180) + center.X); pt.Y = (float)(radius * Math.Sin(angle * Math.PI / 180) + center.Y); return pt; }
把代码加到Paint事件画圆的后面，看看效果。
Yeah, baby，你太听话了。
永不满足的客户·永不结束的工作
没过半天，客户就找到boss，要求在辐射线边上加上角度数字。于是，我「义不容辞」的开始了新一轮改造。
说起加上数字，先前我已经得到了每个射线终点的坐标，那我直接在那坐标上DrawString()出角度数字就行了吧？嗯，在void drawCrosshair()里面先加上这句试试。
|
1
2
|
// 画角度值 g.DrawString(angle.ToString("0") + "°", this.Font, Brushes.Gray, endPoint); |
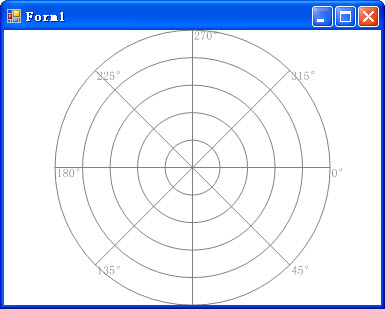
哦，卖糕的，问题多多哦。最下面的字跑出画面了，上面的和左边的字跑到圆圈里面，右边的字也有点往里靠。改改试试看。先把画圆的区域缩小一点，以便下面的标签能显示出来。
|
1
2
3
4
5
|
//drawDiagramCircles(e.Graphics, this.ClientRectangle); // 缩小点画圆的区域 Rectangle rect = this.ClientRectangle; rect.Inflate(0, -20); drawDiagramCircles(e.Graphics, rect); |
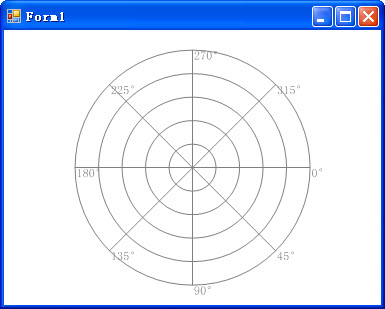
ok，解决下一个问题。先思考下，什么情况下字会跑到圆里去：θ∈(90°, 270°)这个区间。那我就在这个区间画文字的时候，把文字往左平移出去就行了。而270°时，我把文字往上移动试试看。在drawCrosshair()画文字的地方。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
// 把要画的字符串提出来便于操作 string angleString = angle.ToString("0") + "°"; // 画角度值，如果文字在90-270度区间内， PointF textPoint = endPoint; if (angle == 270) textPoint.Y -= TextRenderer.MeasureText(angleString, this.Font).Height; // 用TextRenderer测量字符串大小 else if (angle < 270 && angle > 90) textPoint.X -= TextRenderer.MeasureText(angleString, this.Font).Width; else textPoint.X += 8; // 随便来点漂移 g.DrawString(angleString, this.Font, Brushes.Gray, textPoint); |
看看效果。
嗯哼，很好。（其实我觉得最好的办法是分象限，比如第一象限就增加x、增加y，第二象限就增加x、减少y，第三象限减少x、减少y，第四象限减少x、增加y）
加入数据点
光画一副坐标系那肯定是什么都干不了的，所以还有最重要的添加数据。所谓一个数据，就是包含了角度、数值的这样一组数，比如天线对着某个方向（角度）的接收信号强度（数值）。角度很好理解，就是0到360°，然后转圈。数值就要费点功夫了。用户添加的数据，肯定是他们采集到的真实数据。这个数据，要映射到我这里做的坐标图里面，使其同样大小数值具有同样的映射点，最小数值映射在圆心，最大数值映射在射线终点。这样，所有的数据就都可以用这张图来记录了。下面使用最简单的线性映射来设计。所谓线性映射，其实就是这样。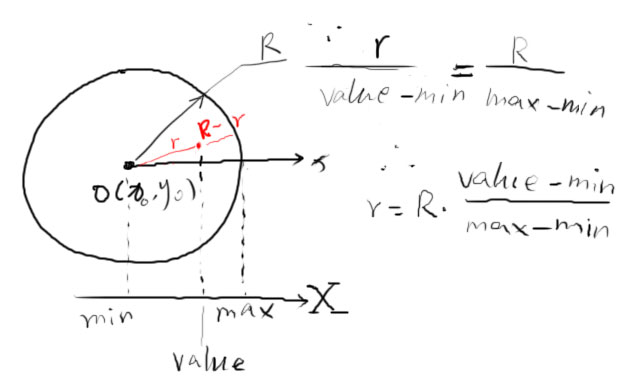
所以，在全局变量里，我加入了数据范围的上下限。（可以任意，只要max大于min，不能等于）
|
1
2
|
float min = 0; float max = 100; |
为了便于后续操作，我决定把「角度 - 数值」这样一组数据封装在一个类里，然后用一个列表来存储管理。
View Code
public class PolarValue { float ang = 0; float val = 0; // 角度 public float Angle { get { return ang; } set { ang = value; } } // 数值 public float Value { get { return val; } set { val = value; } } public PolarValue(float angle, float value) { this.ang = angle; this.val = value; } } // 数据列表 public List<PolarValue> values = new List<PolarValue>();
现在我有了一组数据点，我需要做的就是把数据点映射到坐标图上，如此遍历每一点并连接之，就画出了我所需要的方向图。这就是映射的方法。
|
1
2
3
4
5
6
7
8
9
10
|
private PointF getMappedPoint(PolarValue pv) { // 计算映射在坐标图中的半径 float r = radius * (pv.Value - min) / (max - min); // 计算GDI+坐标 PointF pt = new PointF(); pt.X = (float)(r * Math.Cos(pv.Angle * Math.PI / 180) + center.X); pt.Y = (float)(r * Math.Sin(pv.Angle * Math.PI / 180) + center.Y); return pt; } |
写到这里，我不由得回头看了看刚才画辐条时，为了计算辐条终点而写的getPoint()方法。这两个方法实在是太像了，唯一区别就是getMappedPoint()使用变化的数值，而getPoint()使用固定的数值（辐条终点可以认为是r=R，即value=max）。现在合并这两个方法，并修改相应调用的地方。
|
1
2
3
4
5
6
7
8
9
10
11
|
// 合并后的映射方法 private PointF getMappedPoint(float angle, float value) { // 计算映射在坐标图中的半径 float r = radius * (value - min) / (max - min); // 计算GDI+坐标 PointF pt = new PointF(); pt.X = (float)(r * Math.Cos(angle * Math.PI / 180) + center.X); pt.Y = (float)(r * Math.Sin(angle * Math.PI / 180) + center.Y); return pt; } |
修改调用的地方
|
1
2
3
4
|
// 在drawCrosshair()中 // （略） // 得到终点 endPoint = getMappedPoint(angle, max); |
现在可以一口气把所有数据点画出来了。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
private void drawPoints(Graphics g, List<PolarValue> pointList) { // 计算下一点 PointF nextPt; for (int i = 0; i < pointList.Count; i++) { if ((i + 1) < pointList.Count) nextPt = getMappedPoint(pointList[i + 1].Angle, pointList[i + 1].Value); else nextPt = getMappedPoint(pointList[0].Angle, pointList[0].Value); // 连接当前点和下一点 g.DrawLine(Pens.Black, nextPt, getMappedPoint(pointList[i].Angle, pointList[i].Value)); } } |
随便添加几个数据，顺便设置下圆圈数和辐条数，看看效果如何。
圆圈=3，辐条=4
圆圈=6，辐条=8
圆圈=9，辐条=16
一些变化
（以下内容为搞笑） 好了，我们做完了这个项目，送走了天线的客户。现在又来了一个游戏的客户。他要求我们要制作一个类似FIFA或者实况的运动游戏，游戏里面要有一个运动员个人素质参数的查看界面。 我们要怎么做？重新做？不，就着上一个客户的稍微那么改上一改，就像这样。
