java实现组合数_n!_杨辉三角_组合数递推公式_回文数_汉诺塔问题
一,使用计算机计算组合数
1,设计思想
(1)使用组合数公式利用n!来计算Cn^k=n!/k!(n-k)!用递推计算阶乘
(2)使用递推的方法用杨辉三角计算Cn+1^k=Cn^k-1+Cn^k
通过数组写出杨辉三角,对应的几排几列就对应这组合数的n和k
(3)使用递归的方法用组合数递推公式计算
定义带参数的方法,将不同的参数传递给方法,然后计算出阶乘
2,程序流程图
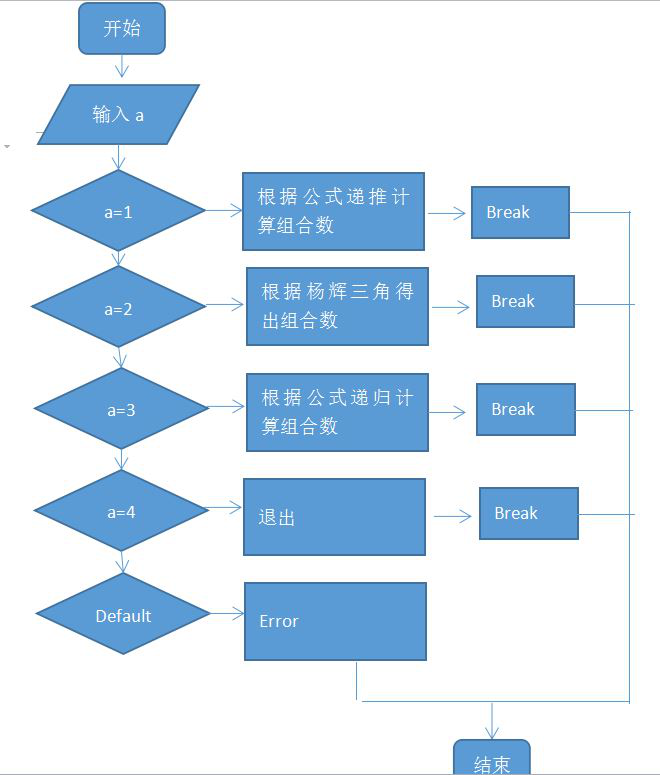
3,程序源代码
package 计算组合数;
import java.util.Scanner;
public class Caculate {
int n,k;//定义私有成员变量
static Scanner input=new Scanner(System.in);
public void caculate1(){
System.out.println("请输入n和k的值");
System.out.print("n:");
n=input.nextInt();
System.out.print("k:");
k=input.nextInt();
if(k>n)
System.out.println("k不能大于n");
else if(k==n)
System.out.println(1);//规定当n=k时 输出1
else{
int a=1,b=1,c=1;//初始化a b c为1
int d=n-k;
while(k!=0||d!=0){//当k和n-k都等于0时循环结束
if(n!=0){
a=a*n;//递推
n=n-1;
}
if(k!=0){
b=b*k;//递推
k=k-1;
}
if(d!=0){
c=c*d;//递推
d=d-1;
}
}
int result=a/(b*c);
System.out.println("Cn^k="+result);
}
}
public void caculate2(){
int a[][]=new int [100][100];
for(n=0;n<10;n++){
a[n][0]=1;
for(k=0;k<=n;k++){
if(n==k)a[n][k]=1;
if(n>k&&k!=0)
a[n][k]=a[n-1][k-1]+a[n-1][k];
System.out.print(a[n][k]+" ");
}
System.out.print("\n");
}
System.out.println("计算组合数\n请输入n和k的值:");
n=input.nextInt();
k=input.nextInt();
System.out.println("由杨辉三角可得知C(n+1)^k的值为:"+a[n+1][k]);
System.out.println("由杨辉三角可得知Cn^(k-1)的值为:"+a[n][k-1]);
System.out.println("由杨辉三角可得知Cn^k的值为:"+a[n][k]);
System.out.println("所以得出:\nC(n+1)^k=Cn^(k-1)+Cn^k");
}
public int caculate3(int n){
if(n==0)
System.exit(0);
if(n==1)
return 1;
else
return n*caculate3(n-1); //递归
}
public static void main(String[] args){
int a;
do{
System.out.println("1,使用组合数公式利用n!来计算Cn^k=n!/k!(n-k)!");
System.out.println("2,使用递推的方法用杨辉三角计算Cn+1^k=Cn^k-1+Cn^k");
System.out.println("3,使用递归的方法用组合数递推公式计算");
System.out.println("4,退出");
a=input.nextInt();
Caculate Ca=new Caculate();
switch(a){
case 1:{Ca.caculate1();System.out.println();}break;
case 2:{Ca.caculate2();System.out.println();}break;
case 3:{
int a1=1,b1=1,c1=1,d1=1,e1=1,f1=1;
System.out.println("组合数递推公式为:Cn^k=C(n-1)^(k-1)+C(n-1)^k");
System.out.println("请输入n和k的值:");
System.out.print("n:");
int n1=input.nextInt();
System.out.print("k:");
int k1=input.nextInt();
//组合数递推公式计算
if(n1-1>=k1){
a1=Ca.caculate3(n1); //计算n!
b1=Ca.caculate3(n1-1); //计算(n-1)!
c1=Ca.caculate3(k1); //计算k!
d1=Ca.caculate3(k1-1); // 计算(k-1)!
e1=Ca.caculate3(n1-k1); //计算(n-k)!
if(n1-1-k1>0)
f1=Ca.caculate3(n1-1-k1); //计算(n-k-1)!
if(k1==0)
System.out.println("Cn^k="+1);
else
System.out.println("Cn^k="+a1/(c1*e1));
if(n1-1==k1-1||k1==1)
System.out.println("C(n-1)^(k-1)="+1);
else
System.out.println("C(n-1)^(k-1)="+b1/(d1*e1));
if(n1-1==k1||k1==0)
System.out.println("C(n-1)^k="+1);
else
System.out.println("C(n-1)^k="+b1/(c1*f1));
System.out.println("由上述结果可得知:Cn^k=C(n-1)^(k-1)+C(n-1)^k");
}
else
System.out.println("error! n不能小于k且n-1不能小于k");
System.out.println();
}break;
case 4:{System.exit(0);}break;
default:System.out.println("error");
}
}while(a!=4);
}
}
4,结果截图


二,汉诺塔问题
1,设计思想
定义hanio方法递归调用直到盘子数量等于1
2,程序流程图
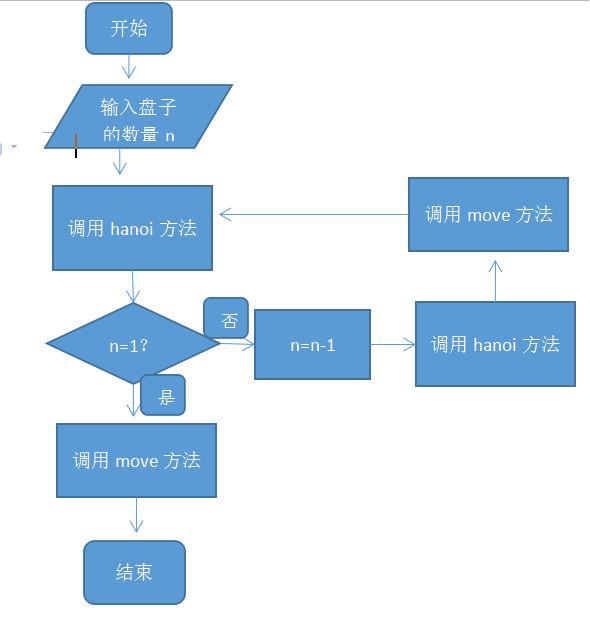
3,程序源代码
package 汉诺塔问题;
import java.util.Scanner;
public class Ta {
public void hanoi(int n,char one,char two,char three){
if(n==1){
move(one,three);
}
else{
hanoi(n-1,one,three,two);
move(one,three);
hanoi(n-1,two,one,three);
}
}
public void move(char x,char y){
System.out.println(x+"->"+y);
}
public static void main(String[] args){
//int A[]=new int[64];
int number;
Scanner input=new Scanner(System.in);
System.out.print("请输入移动的盘子数量:");
number=input.nextInt();
System.out.println("假设有三个底座A、B、C,那么移动盘子的过程如下:");
Ta t=new Ta();
t.hanoi(number,'A','B','C');
}
}
4,结果截图

三,使用递归方式判断某个字符串是否回文
1,设计思想
(1)先输入一个字符串传参进入huiWen方法中
(2)将输入的字符串想加传给temp2
(3)将temp2倒序传给temp1
(4)判断:如果字符串temp1和temp2相同,则回文;否则输出不回文的字样并提示用户继续输入
(5)如果不是回文则调用方法自身继续输入字符串
2,程序流程图
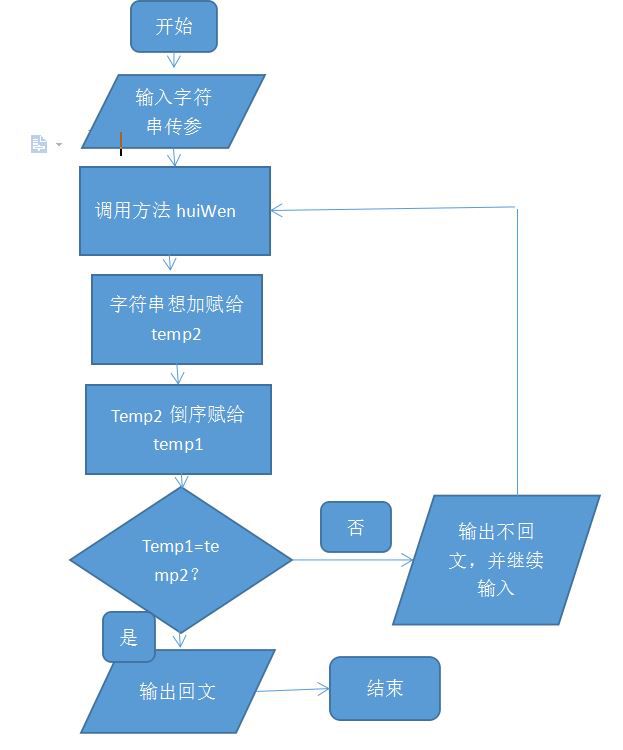
3,程序源代码
package 递归判断字符串是否回文;
import java.util.Scanner;
public class Judge {
String temp2=" ",temp1;
Scanner input=new Scanner(System.in);
public void huiWen(String s1){
temp2=s1+temp2;
temp1=reverseString(temp2); //调用reverse方法使字符串temp2倒序
if(temp2.equals(temp1)){
System.out.println("该字符串回文");
System.out.println("原字符串:"+temp2);
System.out.println("现字符串:"+temp1);
}
else{
if(!temp2.equals(temp1))
System.out.println("以上字符串不回文,请继续输入");
huiWen(input.nextLine()); //调用自身继续输入字符串
}
}
public static String reverseString(String string){ //使字符串倒序的方法
StringBuffer buf=new StringBuffer();
buf.append(string);
return buf.reverse().toString();
}
public static void main(String[] args){
Scanner input=new Scanner(System.in);
Judge j=new Judge();
System.out.println("请输入一个字符串,直到输入空格结束:");
j.huiWen(input.nextLine());
}
}
4,结果截图





 浙公网安备 33010602011771号
浙公网安备 33010602011771号