[Atcoder Grand Contest 004] Tutorial
Link:
A:
……

#include <bits/stdc++.h> using namespace std; long long a,b,c; int main() { scanf("%lld%lld%lld",&a,&b,&c); if(a%2==0||b%2==0||c%2==0) puts("0"); else printf("%lld",min(a*b,min(a*c,b*c))); return 0; }
B:
从0到$n-1$枚举$k$
对于每一个$k$,$res=k*x+\sum_{i=1}^n min(dat[i-1],dat[i-2],..dat[i-k])$
接下来对于每个$i$预处理出$pre[i][j]$表示第$i$个数及其之前$j$个数中的最小值
这样就能在$O(n)$内算出每个$k$时的结果

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int MAXN=2005; ll x,res=1e15; int n,pre[MAXN][MAXN]; int main() { scanf("%d%lld",&n,&x); for(int i=0;i<n;i++) scanf("%d",&pre[i][0]); for(int i=0;i<n;i++) for(int j=1;j<n;j++) { int cur=(i-j+n)%n; pre[i][j]=min(pre[i][j-1],pre[cur][0]); } for(int i=0;i<n;i++) { ll t=i*x; for(int j=0;j<n;j++) t+=pre[j][i]; res=min(res,t); } printf("%lld",res); return 0; }
C:
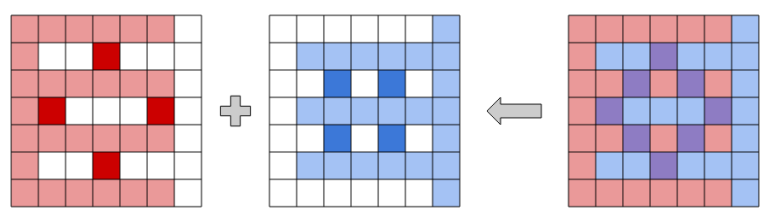
纯构造题
虽然算是奇技淫巧,但还是有些规律可循的……
一个条件:边界上没有紫色的部分
这其实就暗示我们要根据这个条件构造连通性,两颜色各占一条边
接下来可以先让两种颜色完全没有重叠,再对应有重叠的部分特殊处理:
1、奇数行(不含边界)为蓝色,偶数行为红色
2、将紫色部分补成两种颜色
这样就既保证只有紫色部分有两种颜色,有保证两种颜色分别连通了!
官方题解的例子:

#include <bits/stdc++.h> using namespace std; const int MAXN=505; int n,m; char a[MAXN][MAXN],b[MAXN][MAXN],dat[MAXN][MAXN]; int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%s",dat[i]+1); for(int i=1;i<=n;i++) { a[i][1]=b[i][m]='#'; if(i&1) for(int j=2;j<=m-1;j++) a[i][j]='#'; else for(int j=2;j<=m-1;j++) b[i][j]='#'; } for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) a[i][j]=(dat[i][j]!='#'&&a[i][j]!='#')?'.':'#', b[i][j]=(dat[i][j]!='#'&&b[i][j]!='#')?'.':'#'; for(int i=1;i<=n;i++) printf("%s\n",a[i]+1); puts(""); for(int i=1;i<=n;i++) printf("%s\n",b[i]+1); return 0; }
感觉构造题还是有一些通用思想的
对于此题,就利用了弱化条件的思想
(1)先不考虑有部分要重叠,只保证无重叠且各自连通
(2)再考虑怎么保证任意添加都不影响连通性
D:
首先能比较简单得证出1必须为自环(否则包含1的环中的其他点一定不满足要求)
此时$n$个点,$n-1$条边形成一棵树,
于是将问题转化为将一棵树切割成高度不大于$k-1$的子树的最小值
(特判:子树的根为1时高度不大于$k$即可)
这样从叶子节点向上贪心选取即可(一定不能从上向下贪心!)

#include <bits/stdc++.h> using namespace std; const int MAXN=1e5+10; vector<int> G[MAXN]; int n,k,dat[MAXN],dp[MAXN],res=0; void dfs(int x)//要从叶子节点开始推! { for(int i=0;i<G[x].size();i++) if(G[x][i]!=dat[x]) dfs(G[x][i]); if(++dp[x]>=k&&dat[x]!=1) res++,dp[x]=0; dp[dat[x]]=max(dp[dat[x]],dp[x]); } int main() { scanf("%d%d",&n,&k); for(int i=1;i<=n;i++) scanf("%d",&dat[i]); if(dat[1]!=1) res++,dat[1]=1; for(int i=2;i<=n;i++) G[dat[i]].push_back(i); dfs(1);printf("%d",res); return 0; }
一般树上递推/贪心都要从叶子节点向上推
从上往下直接贪心一般都有问题
E:
把所有机器人的移动看成出口的移动
这样出口每向一个方向移动一格会ban掉相反方向的一整行/列
而产生的贡献的长度由其向垂直的两个方向移动的距离及产生的限制限定
这样设$dp[u][d][l][r]$表示出口已向四个方向移动$u,d,l,r$后的最值,加个前缀和$O(1)$算贡献即可

#include <bits/stdc++.h> using namespace std; #define X first #define Y second #define pb push_back typedef double db; typedef long long ll; typedef pair<int,int> P; const int MAXN=101; char s[MAXN][MAXN]; int n,m,x,y; short dp[MAXN][MAXN][MAXN][MAXN]; short line[MAXN][MAXN],col[MAXN][MAXN]; void upd(short &a,short b){a=max(a,b);} int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { scanf("%s",s[i]+1); for(int j=1;j<=m;j++) { if(s[i][j]=='E') x=i,y=j; line[i][j]=line[i][j-1]+(s[i][j]=='o'); col[i][j]=col[i-1][j]+(s[i][j]=='o'); } } short res=0; dp[0][0][0][0]=0; for(int u=0;u<x;u++) for(int d=0;d<=n-x;d++) for(int l=0;l<y;l++) for(int r=0;r<=m-y;r++) { if(!(u+d<max(x,n-x+1)&&l+r<max(y,m-y+1))) continue; short &cur=dp[u][d][l][r];res=max(res,cur); int L=max(r+1,y-l),R=min(y+r,m-l),D=min(x+d,n-u),U=max(x-u,d+1); if(u+1+d<x) upd(dp[u+1][d][l][r],cur+line[x-u-1][R]-line[x-u-1][L-1]); if(d+1+u<=n-x) upd(dp[u][d+1][l][r],cur+line[x+d+1][R]-line[x+d+1][L-1]); if(l+1+r<y) upd(dp[u][d][l+1][r],cur+col[D][y-l-1]-col[U-1][y-l-1]); if(r+1+l<=m-y) upd(dp[u][d][l][r+1],cur+col[D][y+r+1]-col[U-1][y+r+1]); } printf("%d",res); return 0; }
F:
$Atcoder$风格神仙题,第一步就想不到系列……
树的情况:
(不能随便找一个点为根贪心,如果要贪心需要枚举所有点为根)
一般此类相邻点同时操作想到黑白染色!
一棵树必然能黑白染色,每次操作就是将两点颜色取反,目标是所有点皆呈反颜色
由于能翻转的条件是必须要一黑一白,那么就能看成黑点的移动,移动一步就要翻转一次
接下来对每条边计算贡献,考虑儿子的子树中黑白点的差$s[i]$,贡献则为$abs(\sum s[i])$
如果总的黑白点数不等则无解
奇环的情况
由于非树边连接的点同颜色,每次操作相当于同时增加/减少2个黑点
因此只有在黑白点差为偶数时有解,此时将$x,y$到根路径上点的$s[i]$修改后再同样计算即可
偶环的情况
非树边连接的点颜色不同,每次操作相当于移黑点,关键在于确定转移数量
设$x,y$到根路径上的点分别为$a_i,b_i$,$x$向$y$转移了$k$
则要求$min{\sum |a_i-k|+|b_i+k|+|k|}$
此式的几何意义就是$a_i,-b_i,0$到$k$的距离和,明显最优$k$就是中位数,同样修改计算

#include <bits/stdc++.h> using namespace std; #define X first #define Y second #define pb push_back typedef double db; typedef long long ll; typedef pair<int,int> P; const int MAXN=1e5+10; struct edge{int nxt,to;}e[MAXN<<2]; ll res=0; int lca,dep[MAXN],sum[MAXN],f[MAXN]; int n,m,fx,fy,head[MAXN],x,y,tot,TOT,cnt,t[MAXN]; void add_edge(int x,int y) { e[++TOT]=(edge){head[x],y};head[x]=TOT; e[++TOT]=(edge){head[y],x};head[y]=TOT; } void dfs(int x,int anc,int val) { sum[x]=val;tot+=val; dep[x]=dep[anc]+1;f[x]=anc; for(int i=head[x];i;i=e[i].nxt) if(e[i].to!=anc) { if(dep[e[i].to]) {fx=x;fy=e[i].to;continue;} dfs(e[i].to,x,-val),sum[x]+=sum[e[i].to]; } } int LCA(int x,int y) { if(dep[x]<dep[y]) swap(x,y); int t=dep[x]-dep[y]; for(int i=1;i<=t;i++) x=f[x]; while(x!=y) x=f[x],y=f[y]; return x; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) scanf("%d%d",&x,&y),add_edge(x,y); dfs(1,0,1); if(m==n-1) { if(tot) return puts("-1"),0; for(int i=1;i<=n;i++) res+=abs(sum[i]); } else if((dep[fx]-dep[fy])%2==0) { if(tot%2) return puts("-1"),0; lca=LCA(fx,fy);tot=-tot/2;res+=abs(tot); for(int k=fx;k;k=f[k]) sum[k]+=tot; for(int k=fy;k;k=f[k]) sum[k]+=tot; for(int i=1;i<=n;i++) res+=abs(sum[i]); } else { if(tot) return puts("-1"),0; lca=LCA(fx,fy); for(int k=fx;k!=lca;k=f[k]) t[++cnt]=sum[k],dep[k]=-1; for(int k=fy;k!=lca;k=f[k]) t[++cnt]=-sum[k],dep[k]=-1; t[++cnt]=0; sort(t+1,t+cnt+1);int val=t[cnt/2]; for(int i=1;i<=n;i++) if(~dep[i]) res+=abs(sum[i]); for(int i=1;i<=cnt;i++) res+=abs(t[i]-val); } printf("%d",res); return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号