[BZOJ 1177] Oil

Link:https://www.lydsy.com/JudgeOnline/problem.php?id=1177

 

Solution:

相当于将大矩形分为3块，取每块中最大的正方形

 

对于此类分成几块的题目，要想到枚举分割线

 

一共只有这6种情况：

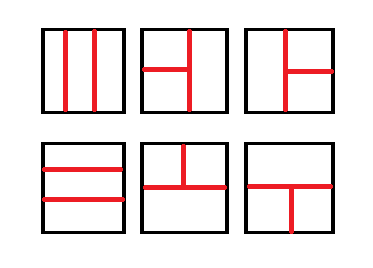
我们只要先预处理左上左下右上右下四个方向最大答案的前缀和，

再对于每种情况枚举分割线即可

 

对于最左边的两种情况，只要将中间一列的宽度保证为k即可

 

Code:

#include <bits/stdc++.h>

using namespace std;
const int MAXN=1500+10;

int n,m,k,t,res=0,s[MAXN][MAXN],a[MAXN][MAXN],b[MAXN][MAXN],c[MAXN][MAXN],d[MAXN][MAXN];

int main()
{
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&t),s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+t;
    for(int i=n;i>=k;i--) for(int j=m;j>=k;j--) s[i][j]-=s[i-k][j]+s[i][j-k]-s[i-k][j-k];
    
    for(int i=k;i<=n;i++) for(int j=k;j<=m;j++) a[i][j]=max(s[i][j],max(a[i-1][j],a[i][j-1]));
    for(int i=k;i<=n;i++) for(int j=m-k+1;j>=1;j--) b[i][j]=max(s[i][j+k-1],max(b[i-1][j],b[i][j+1]));
    for(int i=n-k+1;i>=1;i--) for(int j=k;j<=m;j++) c[i][j]=max(s[i+k-1][j],max(c[i+1][j],c[i][j-1]));
    for(int i=n-k+1;i>=1;i--) for(int j=m-k+1;j>=1;j--) d[i][j]=max(s[i+k-1][j+k-1],max(d[i+1][j],d[i][j+1]));
    
    for(int i=k;i<=n;i++) for(int j=k;j<=m;j++) res=max(res,a[i][j]+b[i][j+1]+c[i+1][m]);
    for(int i=n-k+1;i>=1;i--) for(int j=k;j<=m;j++) res=max(res,c[i][j]+d[i][j+1]+a[i-1][m]);
    for(int i=k;i<=n;i++) for(int j=k;j<=m;j++) res=max(res,a[i][j]+c[i+1][j]+d[1][j+1]);
    for(int i=k;i<=n;i++) for(int j=m-k+1;j>=1;j--) res=max(res,b[i][j]+d[i+1][j]+c[1][j-1]);
    
    for(int i=2*k;i<=n;i++) for(int j=k;j<=m;j++) res=max(res,s[i][j]+a[i-k][m]+c[i+1][m]);
    for(int j=2*k;j<=m;j++) for(int i=k;i<=n;i++) res=max(res,s[i][j]+a[n][j-k]+b[n][j+1]);
    
    printf("%d",res);
    return 0;
}

 

Review:

由求三块权值和最大的不交叉的正方形  ------->  将矩形分为3块  -------->  枚举分割线

 

碰到求不相交的最值问题时，想到切割+枚举切割线的方法