4.4 Graph Nerual Networks(GNN)
1. Introduction
GNN简单来说就是Graph + Nerual Networks,关键问题就是将图的结构和图中每个节点和边的特征转化为一般的神经网络的输入(张量).
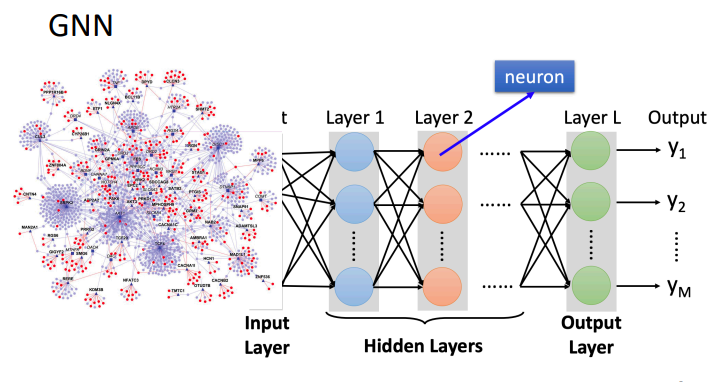
1.1 Why do we need GNN?
GNN可以做的事情主要包括:分类和生成.
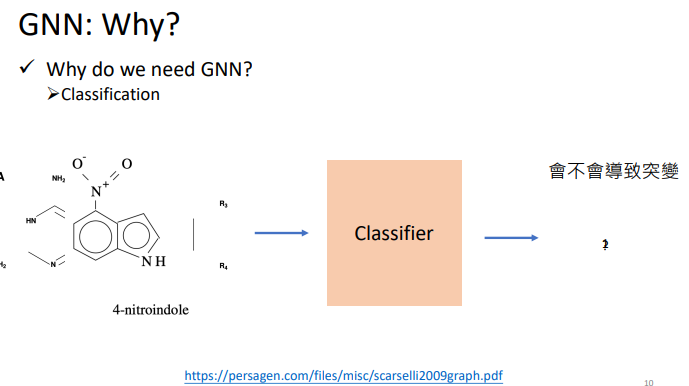
1.2 How can we train GNN model
我们将图作为输入的时候,很容易遇到如下问题,这种问题要怎么解决呢?
我们联想到做CNN的时候,当输入一个很大的\(image\)时,我们使用卷积核来获得它的\(feature\ map\).但这个要怎么generalize到graph上呢?
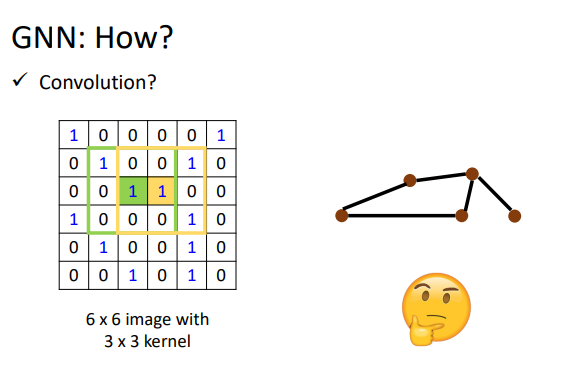
这里有两种解决思路:基于空间的卷积(Spatial-based convolution)和基于频域的卷积(Spectral-based convolution)
2. GNN Roadmap
本章的主要内容如下:
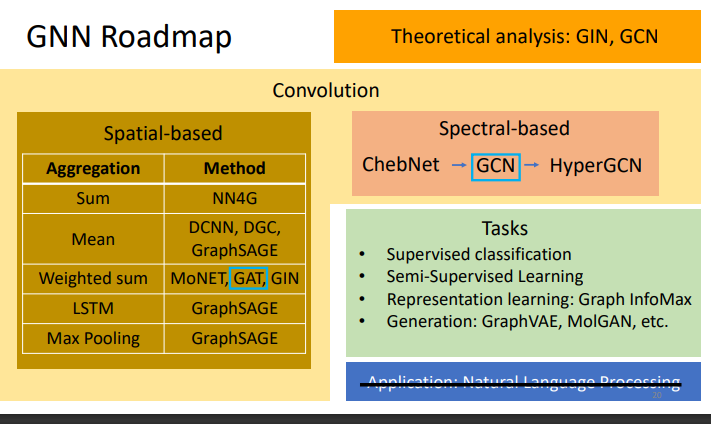
2.1 Tasks, Dataset, and Benchmark
我们提出一个模型必须说明这个模型到底有多好.但是如果不同的人用不同的数据集,衡量标准就很难定义.因此下面是GNN模型评价性能的共同标准:
3. Spatial-based GNN
主要的思想就是模仿之前的卷积操作，之前的卷积操作的是某个点的所有邻居,因此在GNN当中也是通过这样的方式下更新下一层(在GNN中叫做aggregation).当然图上所说的Aggregate也会包括这个节点本身的特征feature.
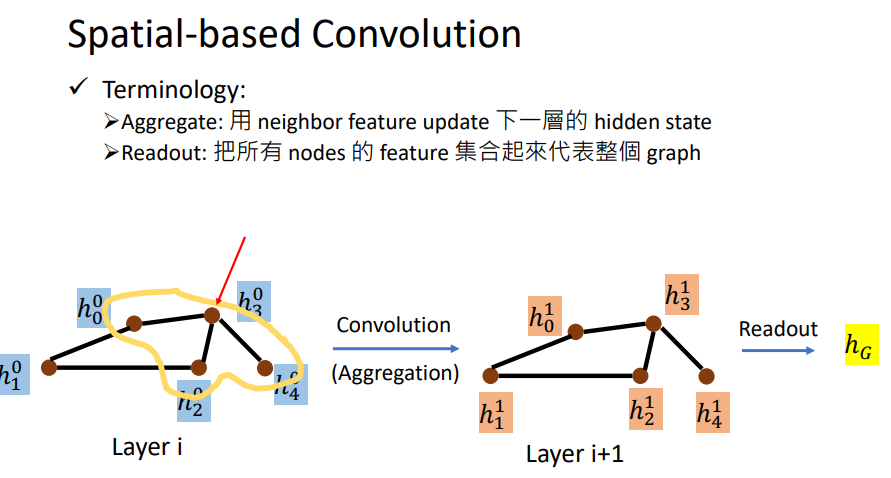
我们得到新一层的每个结点的\(feature\),但是最后还是要得到整个图的\(feature\),这个操作叫做readout.我们可以拿这个做prediction或classification.
3.1 NN4G (Neural Networks for Graph)
这里开始介绍实际的Model.
input layer经过embedding之后到hidden layer 0。然后更新的话是将其相邻的节点相加然后乘以权重再加上之前input layer的原始输入。
关于为什么要相加的问题：如果不用相加的话，你就很难去处理节点间邻居数量不同这个巨大的区别 。另外，相加是最简单也是被证实最有效的利用邻点信息的方法。
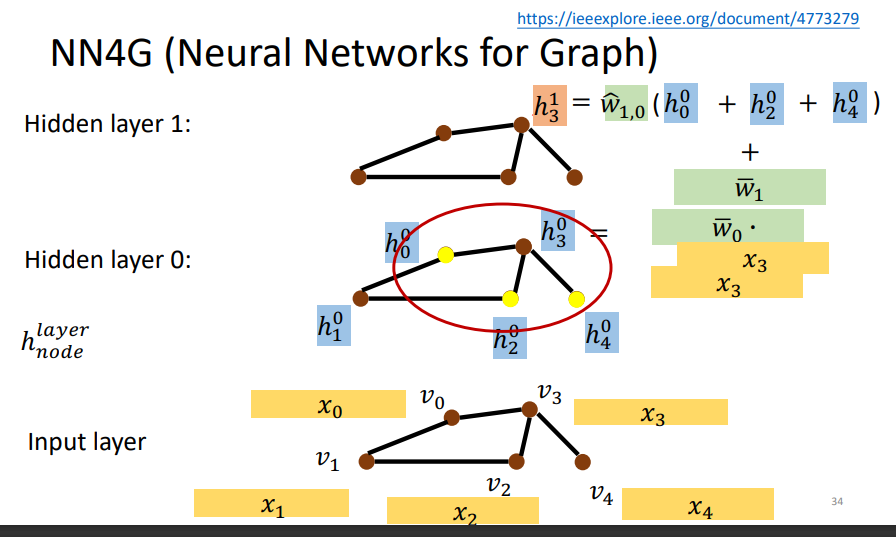
下图是如何得到readout.整个图的表示是通过求出每一层整个图中的顶点间的特征均值，然后各自乘以相应的权重再把每一层得到的结果相加。
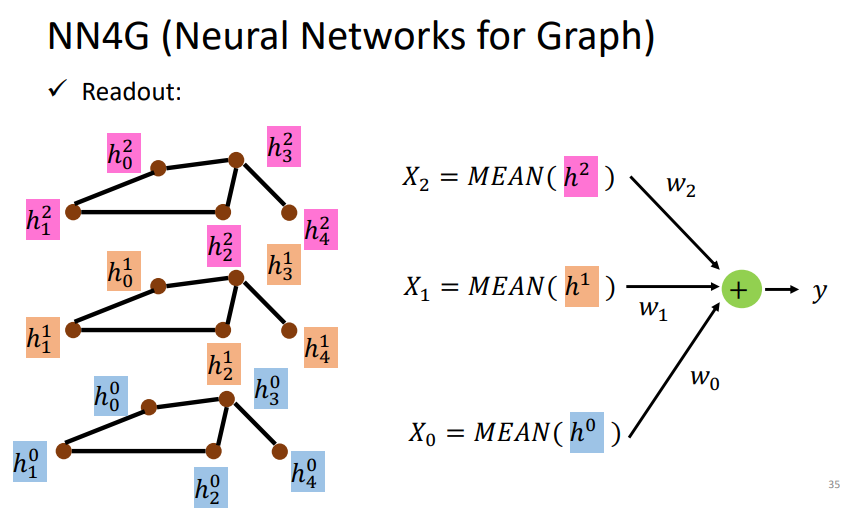
3.2 DCNN(Diffusion-Convolution Neural Network)
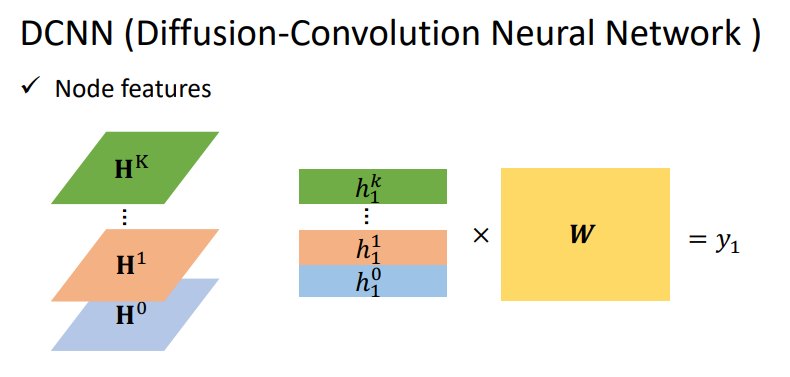
每一层的更新方式：如第一层，更新某个节点首先找到与它距离为1的节点（也就是邻居节点），然后用原始的输入相加取平均值再乘以权重。第二层，更新更新某个节点首先找到与它距离为2的节点（这样也包括了它自自己本身）.然后用原始的输入相加取平均值再乘以权重。
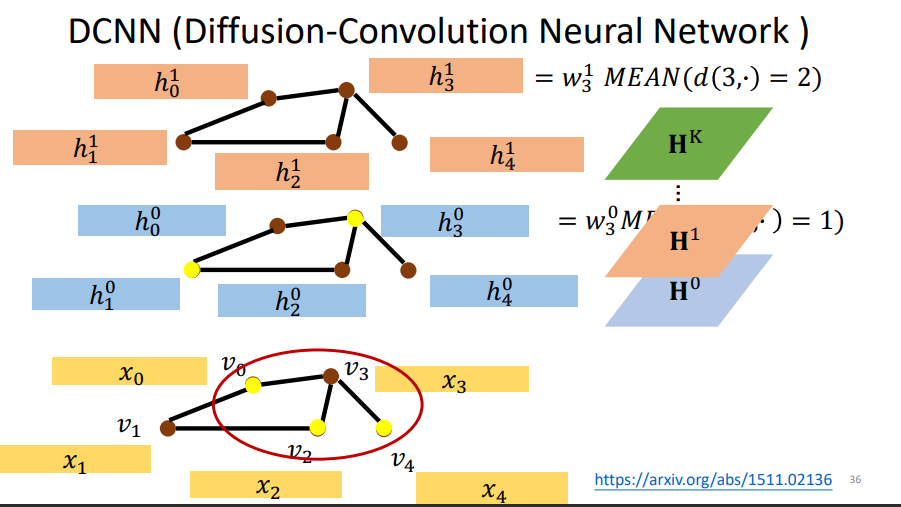
d(3,·) = 1表示与3号结点距离为1的结点.
这样就可以将每一层的节点特征组成一个矩阵，然后叠在一起。当我们需要整个图的feature时候，采用一下的方式来表示图中每个节点的特征：
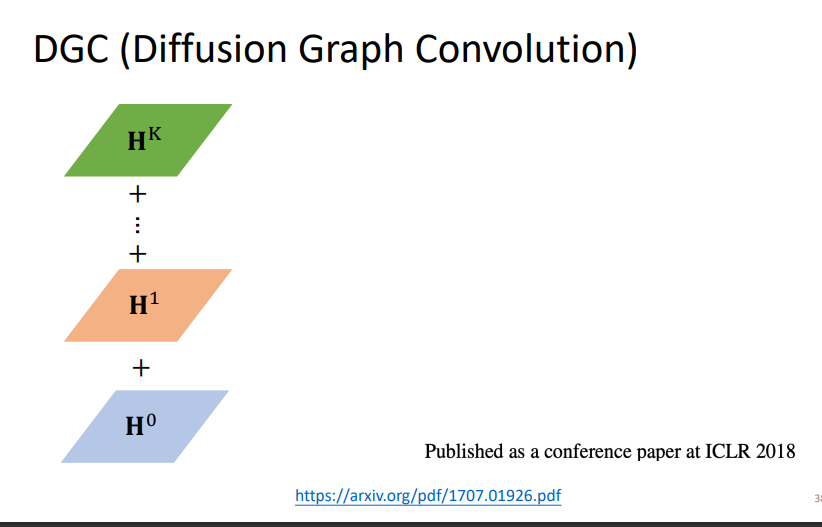
3.3 DGC (Diffusion Graph Convolution)
与上面不同的是,DGC是将叠加的矩阵全部加起来.但是直接相加没有考虑到每层代表距离之间的权重,下面的model处理这个问题.
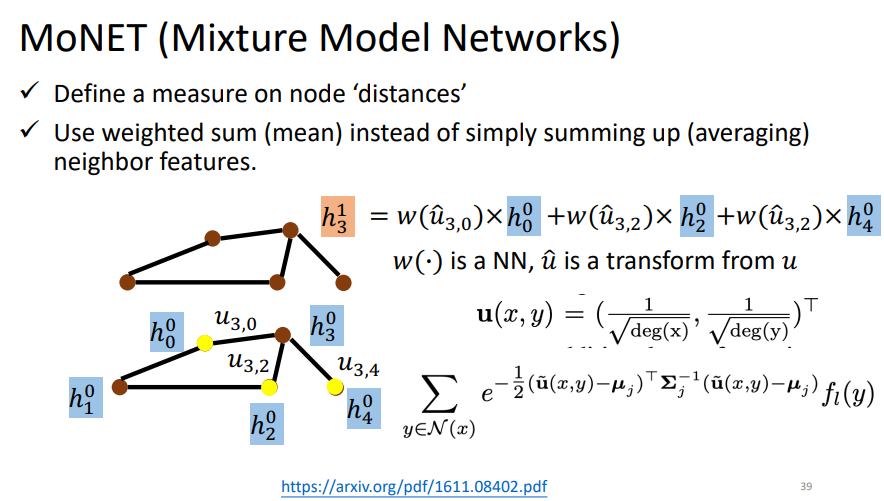
3.4 MoNET (Mixture Model Networks)
之前只是简单的相加，并没有考虑到一个节点的邻居跟之间的区别(有的邻居可能更重要一点).
其中的deg表示的是节点的度.无向图当中也就是说有几个和它相连接的节点.这里定义的距离公式是不同的(可以自己定义),可以看成每个节点不同的权重weighted sum.
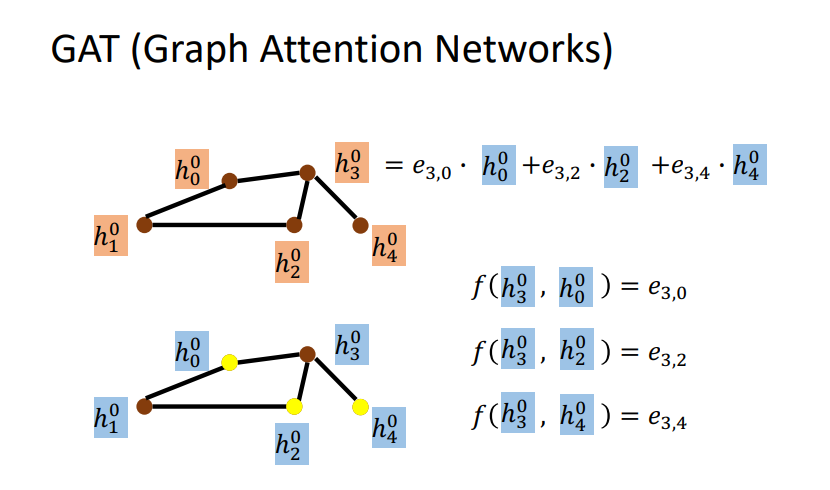
3.5 GAT (Graph Attention Networks)
不止是简单的weighted sum, 不是像之前那样定的weight ，而且要让他自己去学习这个weight。对邻居做Attention,就是不同的邻居给出不同的weight.
这是目前应用最广的.\(f(i,0)\)是一种方式计算\(energy\)表示\(i\)对0有多重要
3.6 GIN (Graph Isomorphism Network)
提供了一些关于图神经网络什么方式的aggregate能够work的理论证明和结论。
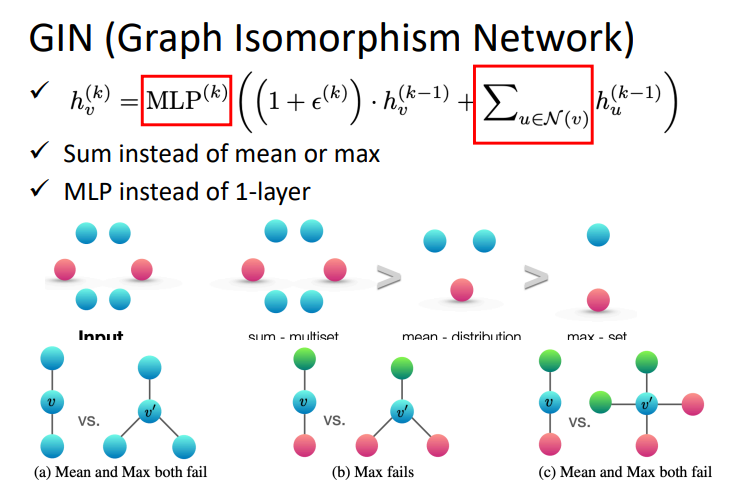
结论就是：用sum的方式，然后用多层感知器而不是一层。
下面的就是例子证明max和mean的缺点。对比的两个图，如果用max或者mean的话是看不出来两个图的区别的。
公式中epsilon可以为\(0\),也可以自己学,因此也就是所有相邻节点和其本身节点相加就可以的。
