3.3 Spatial Transformer

请复习线性代数

1. Spatial Transformer Layer

1.1 CNN is not invariant to scaling and rotation

(1) CNN并不能真正做到scaling和rotation.
(2) 如下图所示,在通常情况下,左右两边的图片对于CNN来说是不一样的.

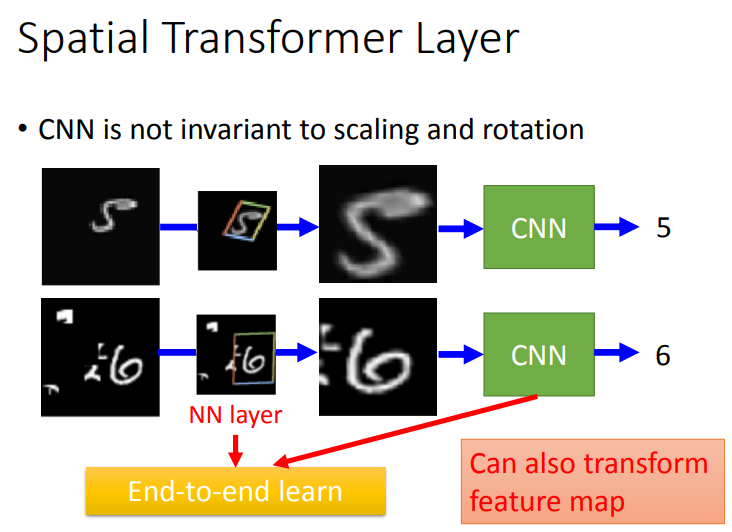
  所以,我们考虑一层layer,这层layer能够对input image进行旋转缩放,以便更好地识别.
  如上图所示,Spatial Transformer Layer是Neuron Network,而它的作用是多学习一层layer,对左边的图片做scaling和rotation后,能够被CNN识别出来.当然,这个Layer也可以transform CNN的feature map.

1.2 How to transform an image/feature map

  Spatial Transformer Layer可以由fully connected neural network训练而来,平移其实是调整weight的过程.如下图所示，weight相同的颜色代表了权值相同,这里就是要将目标向下移动.

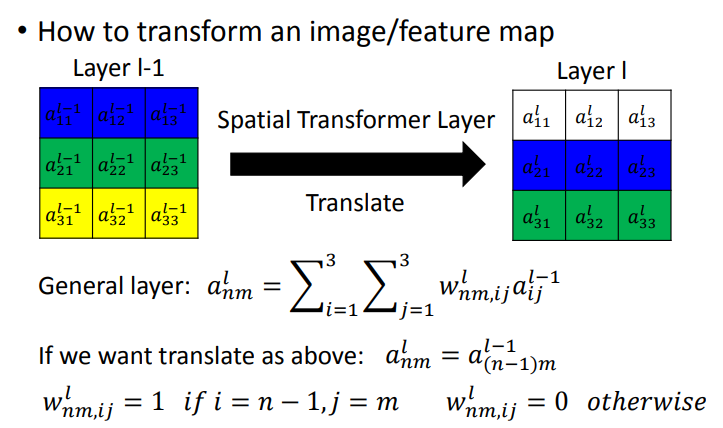
  所以将\(weight\)做不同的设计,就能做到旋转平移.比如,我们要将\(Layer\ l-1\)按红箭头平移.把\(a_{13}^{l-1}\)移动到\(a_{23}^{l}\)的位置上,\(a_{13}^{l-1}\)与\(a_{23}^{l}\)的权值为1,\(a_{23}^{l}\)与左图的其他位置连接\(w\)为0.
  再比如向右旋转,把\(a_{13}^{l-1}\)移动到\(a_{33}^l\)的位置上,\(a_{13}^{l-1}\)与\(a_{33}^l\)对应的\(w\)是1,\(a_{33}^l\)与左图的其他位置连接\(w\)为0.

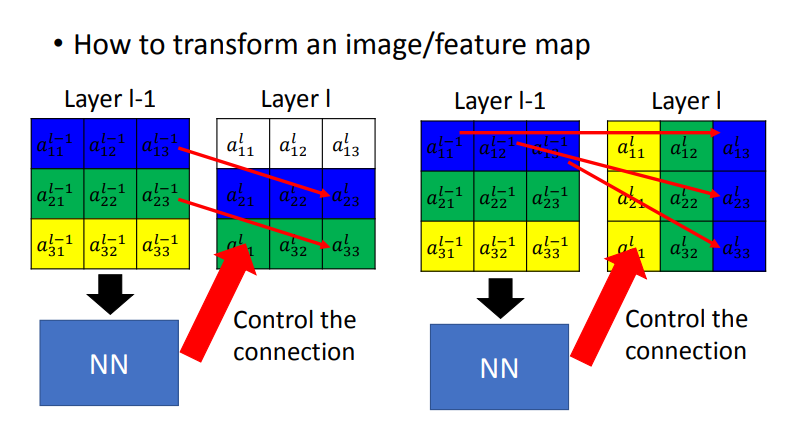
  显而易见,我们只要适当的\(w\)就能做到选择缩放,但问题是怎么找这些\(w\)呢?这里我们使用\(NN\)来连接,也就是我们将\(Layer\ l-1\)的输出放入NN的输入,然后NN的输出来决定\(layer\ l\)与\(layer\ l-1\)的连接方式.

2. Image Transformation

  以图片的例子来说明.我们将图片中的每一个像素坐标化,我们将某个像素的坐标\([x,y]\)移动到新坐标\([x',y']\),只要妥当设计这两点的关系,就能将\(image\)放大.比如乘上参数2,不做平移,即可放大.图下范例为缩小两倍并且移至右上，因此乘上参数0.5最后加上平移值0.5.

  如果要做旋转,可以使用\(sin\)或者\(cos\).

  因此,要将图片旋转缩放的话,实际只需要6个参数.

  所以我们用来转换的NN,实际只需要输出6个参数而已.

  刚才说的是很刚好的得到的解都是整数,但如果不是的话就会有上图的结果,\(a_{22}^l\)接到小数点的索引,但这种索引是不存在的，因此我们可以将计算所得的索引取四舍五入，得到\(a_{22}^{l-1}\),怪怪的对吧,不能这么做.

  注意到,这种情况下是无法利用梯度下降来求解的,梯度是一种将参数做小小的变化,它对Output会有多少影响.如果对Spatial Transformer Layer的NN参数做小小的改变,也许\(x'y'\)变为1.61,2.39.但四舍五入之后它接到的位置还是一样,代表Output没有任何变化,因此微分是0.这样没法更新.

3. Interpolation

  要处理小数点问题,就需要利用Interpolation，求出来的数值是有小数的,而这个小数索引实际上是在四个点的区间内,我们不单纯的参考它跟距离最近的那个点的\(a_{22}^{l-1}\),而是四个点的数值都参考.

  这种情况下NN参数有些微的变化的时候Output也会有些微的变化，就可以利用梯度下降来优化求解了。

4. Spatial Transformer Layer Structure

• U: Input的Image，也可以是feature map，因此画成立方体。
• Localisation net: 稍早所提会Output六个参数的NN
  
    用菱形来表示，搭配手写辨识，它不仅可以放置于Input后面，也可以放置于任何feature map的后面，同一层conv layer后面也可以放多个Transformer layer