2.6 再探宝可梦、数码宝贝分类器 — 浅谈机器学习原理-2022
1. 引入问题
在之前的课程中,我们对"参数过多就会导致过拟合"这个概念处于提出但没有证明的状态,现在来以宝可梦和数码宝贝的分类例子来说明这个问题.
2. 分类器定义
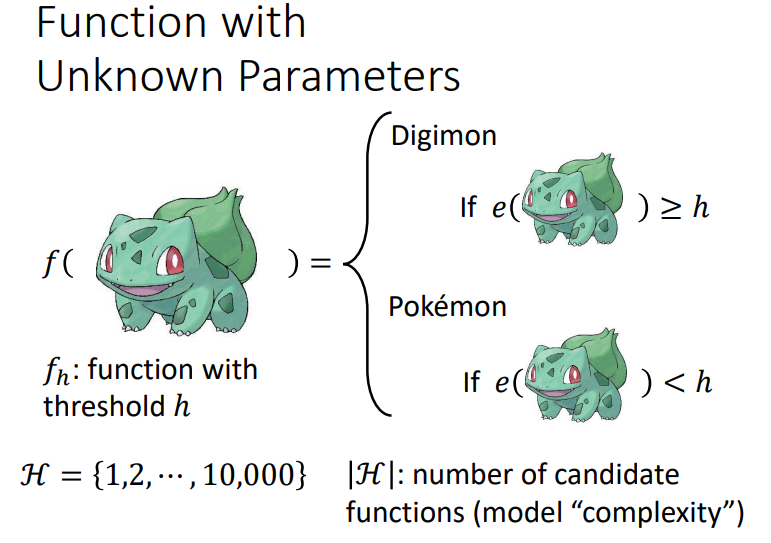
我们观察宝可梦和数码宝贝的图片可以发现,宝可梦的图片线条比较少,而数码宝贝的线条比较多.或许可以以边缘检测探查线条数量作为分类器.图中\(e\)是一个function来检测图片线条的数量.将宝可梦和数码宝贝区分开的门槛是\(h\),\(h\)是一个未知的参数,我们将\(h\)的集合定义为\(H\).\(|H|\)意为\(h\)的待选值个数,也称为模型的复杂程度.也就是定义模型的参数可选择很多,也称为模型复杂程度高.
3. Loss function 定义
给予一个数据集\(D\),一个门槛\(h\)来计算\(loss\).取所有数据集loss的平均值作为dataset D的loss.\(l\)计算\(loss\)的方式可以有很多,蓝色方框是将\(f_h(x^n)\)与\(\hat y^n\)做对比,如果一样就输出\(1\),不一样就输出\(0\).

4. Training Examples
定义了loss function后,假设我们拥有所有的宝可梦和数码宝贝作为数据集,那我们就可以将所有的数据集放在上面计算,然后找到最好的门槛\(h\).这里不适合用梯度下降,因为无法微分,使用枚举就可以了.
但实际上是很难收集全部的数据,只能取一些范例,一般会假设这些范例是由完整数据集\(sample\)出来的,每次\(sample\)都假设为独立同分布,然后希望两者计算出的\(h\)代入\(L(h,D_{all})\),两者\(loss\)尽量接近.

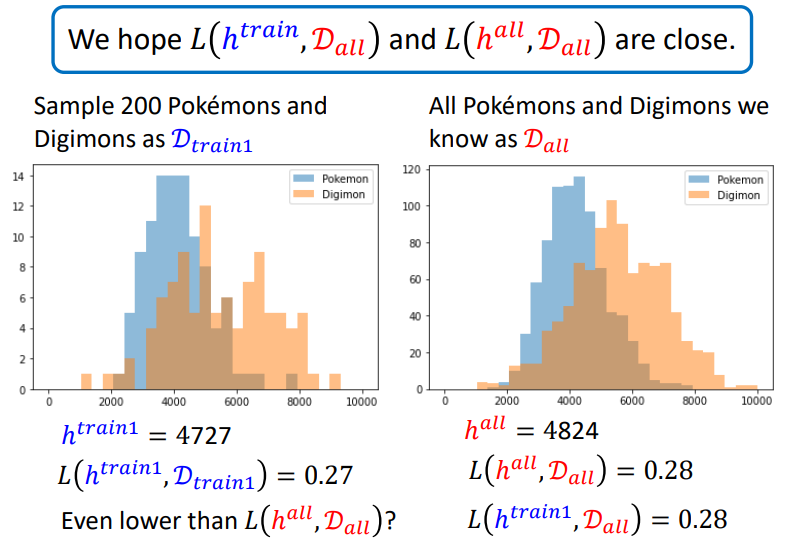
取819只宝可梦,971只数码宝贝,假设这个数字与真实数据很接近,以至于当成真实数据.绘制这些生物(?)的线条与对应数量的条状图.可以计算最好的\(h\)是4824,对应的\(loss\)是0.28

再实践\(sample\)数据作为训练集.训练集分布如下,可以计算出此训练集最好的\(h\)是4727.
我们可以多测试几次.
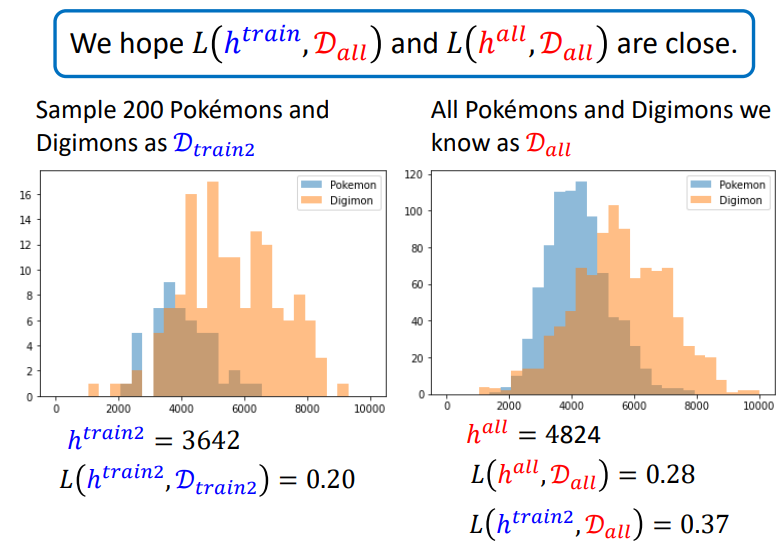
我们用数学式表达就是这样:

那么怎样才能让数学式得到满足呢?当\(D_{train}\)满足上图下面的式子即可.下面的式子代表了\(D_{train}\)和\(D_{all}\)很像.数学推导见下图,将第二个蓝色框的数学式子作为条件去推导第一个蓝色框的结论:

5. Probability of Failure
如果\(D_{train}\)满足第二个蓝色框才算成功,那么\(sample\)失败的概率有多大呢?

上图每个点代表一组训练资料,怎么计算橙色点的概率有多大?直接一个个点算显然很麻烦.有一个方法来估测:
设\(P(D_{train}\quad is\quad bad\quad due\quad to \quad h_1)\)为训练集因为\(h_1\)阈值而不好的概率.以此类推,其他定义

\(sample\)失败的概率就是这些概率的并集,它不会大于这些概率纯粹相加.

首先需要思考一下\(P(D_{train}\quad is\quad bad\quad due\quad to \quad h_1)\)怎么计算.参考下图它的定义,在所有训练集上作平均是\(L(h,D_{all})\).

加入Loss满足条件的话,就有霍夫丁不等式(Hoeffding's inequality):

代入第一个红框有:

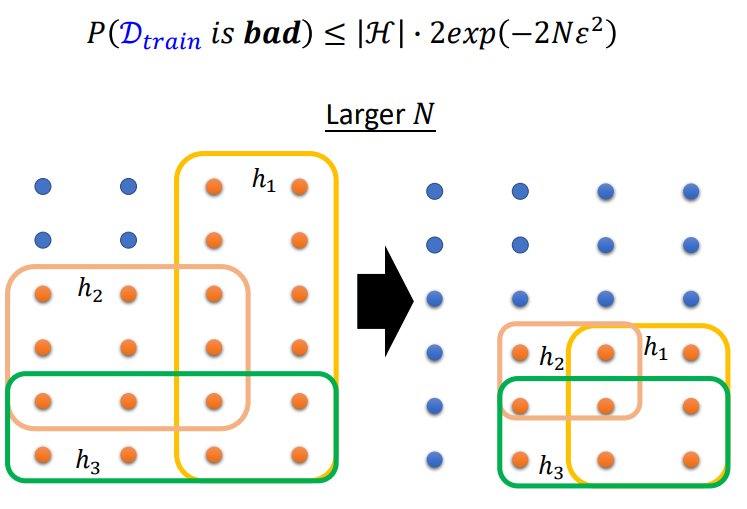
那么怎么让失败的概率变小呢?\(N\)(训练资料的数目)越大,概率会越低,同理\(h\)可取的范围越少,概率也会越低.
将\(N\)调大的效果,\(h\)将训练集弄坏的概率就会降低:
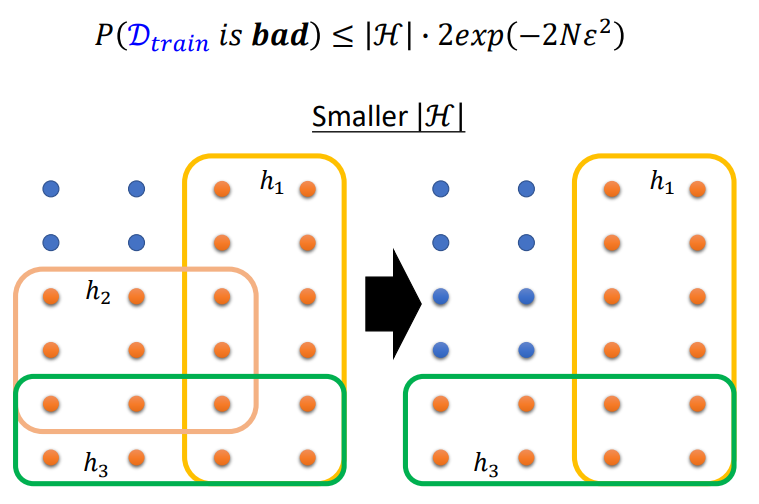
H调小的效果:
6. 公式 Example
N是训练集大小,\(\varepsilon\)是自己定义的,下面是几个例子:

公式经常计算出来\(>1\),所以在实际应用很少使用.这个公式的本来意义是解释训练集和模型复杂度为机器学习的影响.
换一个角度考虑,如果希望\(sample\)出坏data的概率小于某个数值:

7. Model Complexity
可能有人会质疑,参数在模型里的取值都是连续的,H根本毫无意义,这个问题有两个回答方向:

第一个回答可能有点牵强,第二个回答实际才是更确切,VC-dimension是一种计算连续取值参数模型复杂度的方法.本节课不介绍.
此外还有一个问题,如果要选择好的\(D_{train}\).为什么不考虑将H调小呢?考虑一下好的\(D_{train}\)的定义,这意味着\(h_{train}\)在\(D_{train}\)和\(D_{all}\)上的loss很接近.但如果减小了H,可能会导致\(L(h^{all},D_{all})\)增大.所以此时即使\(h_{train}\)在\(D_{train}\)和\(D_{all}\)上的loss很接近,但Loss很大也没有意义了.

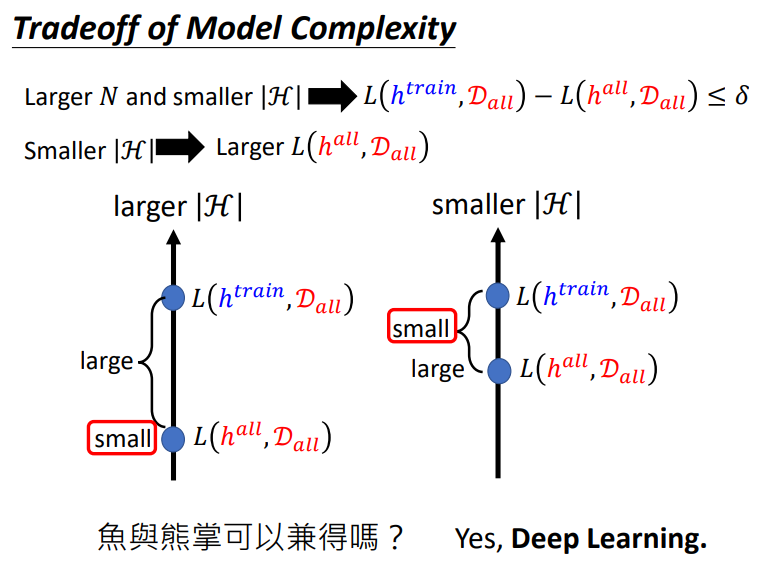
8. 两难困境
\(H\)和loss取舍问题.我们想要\(L(h^{all},D_{all})\)很小,又希望理想与现实之间比较接近.能做到这两件事的就是深度学习.