2.3 类神经网路训练不起来怎么办 (三):自动调整学习速率 (Learning Rate)
1. 自适应学习率调整(Adaptive Learning Rate)
1.1 为什么需要调整学习率
首先认识一个现象.Training stuck ≠ Small Gradient
训练卡住的原因不一定是因为 gradient 太小,即critical point,也有可能是因为振荡.
怎么看出是因为振荡导致训练 loss 降不下去呢:在训练过程中,gradient的大小有较大的波动(红色框中),loss的变化可能就是左图的绿箭头.而产生振荡的原因就是learning rate设定太大.
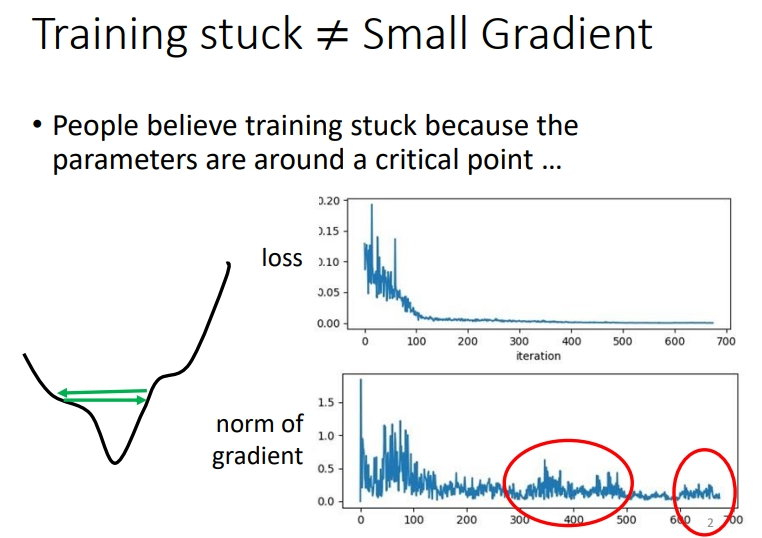
实际上,如果仅仅使用gradient下降的方式,是很难走大局部最小点或者鞍点的,我们往往需要采用其他优化方式.比如下面那张图,使用gradient下降的方式是很难画出来的.所以在实际训练中,如果训练卡住了不一定是因为 critical point.
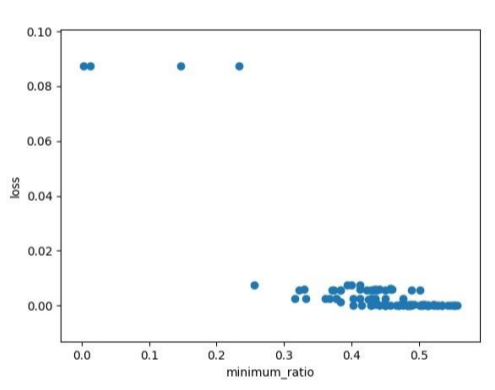
1.2 为什么非critical point训练也可能被卡住
我们举一个简单的例子.有个error surface 是凸面,横轴参数的loss变化很小,而纵轴参数的loss变化快,坡度陡峭.黑点是初始点,叉叉是 loss 最低点.假如设置个较大的 learning rate,纵轴参数更新时会振荡;假如设置个较小的 learning rate,纵轴参数能较好更新,而横轴参数却更新很慢,因为横轴坡度本来就平缓,再设个小的 lr 更新速度当然更慢了!!所以没有哪个 learning rate能一劳永逸,适应所有参数更新速度!!
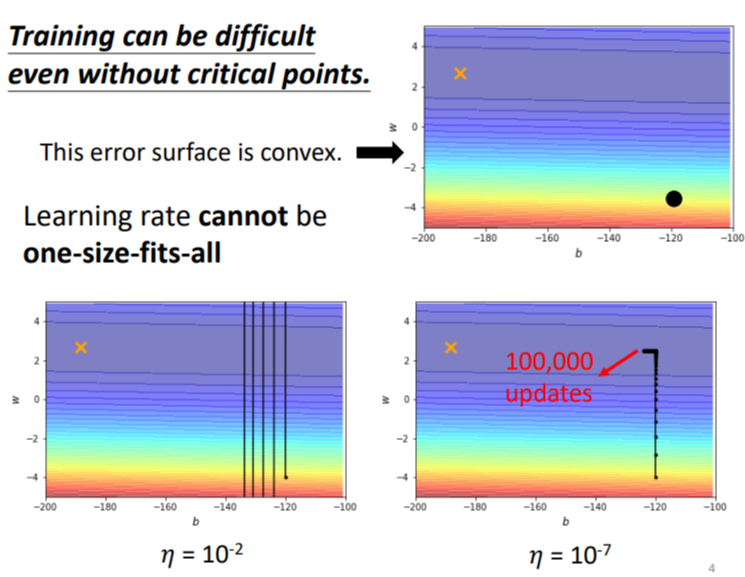
1.3 对参数特制化
我们在参数更新时,其实有一个大原则:不同的参数采用不同的 learning rate,当参数变化快时,设定小的 learning rate 防止振荡;当参数变化慢时,设定大的 learning rate 加快更新速度.那么我们要怎么做到这一点呢?
(1) 对于一个参数而言,使用常规的梯度下降法,参数更新方式为:

(2) 对于一个参数而言,使用自适应的学习率\(\eta\)的梯度下降法,参数更新方式为:

注意:不同的参数要给不同的\(\sigma\).同时它也是iteration dependent的,不同的iteration我们也会有不同的\(\sigma\).
1.4 计算\(\sigma\)的方式
对于\(\sigma\)可以采取不同的计算方式.
1.4.1 Root Mean Square
一种常见的计算方式是计算gradient的Root Mean Square.

利用root mean square计算\(\sigma\)的方法通常使用在Adagrad中.那么为什么会有自适应的效果呢?
这个方法算出来的\(\sigma\)可理解成梯度的平均值.当整体的梯度 g 越大,即越陡,\(\frac{g}{\sigma}\)就会越小!从而减小了更新步伐大小.蓝色曲线的 loss 曲线总体趋势更加平缓,就是整体梯度更小,算出来的\(\sigma\)就会比较小,更新的时候就会有更大的步伐.
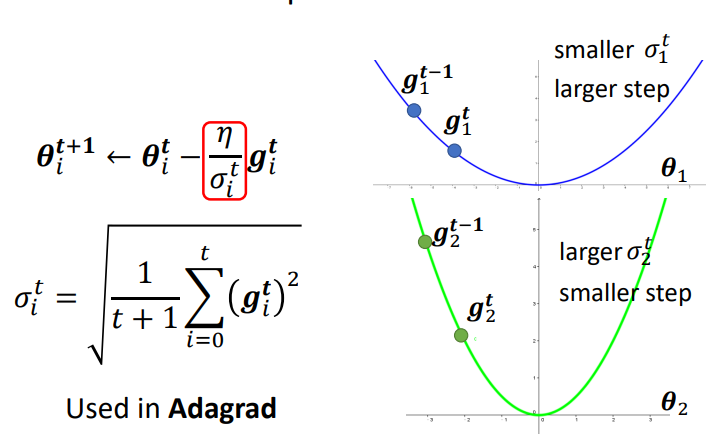
这个方法当然也存在问题.这个方法将同一个参数的gradient视为均匀变化的.但实际上同一个参数不一定是均匀变化的,比如下图:
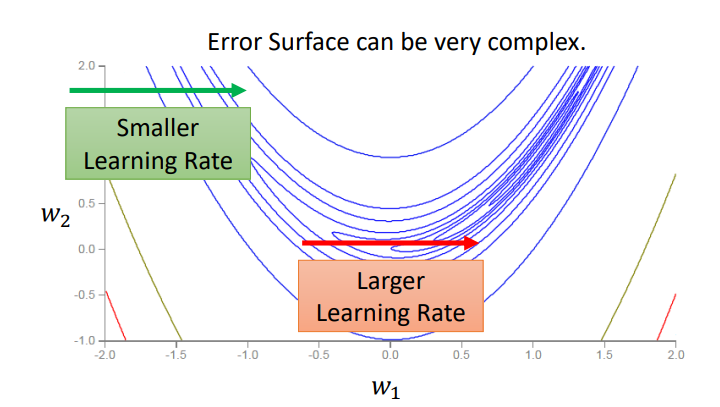
但我们期待同一个参数的 learning rate 能随其位置而变化.在loss 变化快的时候,有更小的 lr;在loss 变化慢的时候,有更大的 lr.
1.4.2 RMSProp
整体思路:Root Mean Square方式中,learning rate随着训练不断降低,可以达到梯度随着训练逐步降低,最终达到收敛的效果.然而当一个参数在训练过程中,其梯度的大小往往会出现实大实小的情况,这个时候需要在梯度较小时采用较大的 learning rate,在梯度较大时采用较小的learning rate,从而保证正确而快速的收敛.
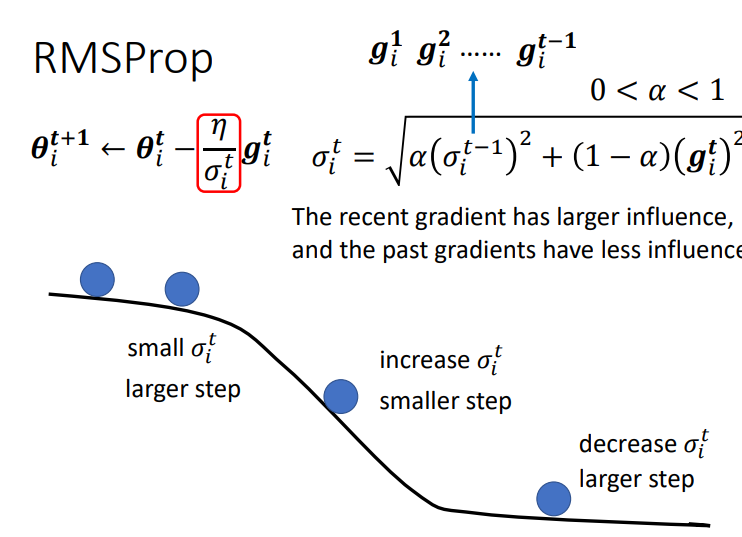
方法:添加参数\(\alpha\),表示当前梯度大小对于 learning rate 的影响比重,是一个超参数(hyperparameter)
- \(\alpha\)设很小趋近于0,就代表这一步算出的 \(g_i\) 相较于之前所算出来的 gradient 而言比较重要.
- \(\alpha\)设很大趋近于1,就代表这一步算出的 \(g_i\) 比较不重要,之前算出来的 gradient 比较重要.
之前的Root Mean Square可以看作各个时刻的梯度占比相同求均值,但这个是占比不同.
![image]()
用图示进一步解释一下,一开始坡度很缓,这时\(\sigma\)会比较小,此时的步子就会比较大(注意是\(\sigma\)而不是\(\alpha\)).当进行到坡度比较大的地方,梯度比较大,就会增大\(\sigma\)(也就是将\(\alpha\)设小一点),从而减小步伐.当回到坡度比较缓的地方,又会减小\(\sigma\),从而让步伐变大.
![image]()
1.4.3 Adam
现在最常用的优化方式是Adam.Adam = RMSProp + Momentum.具体的论文链接在Click.在课上并没有细讲.

1.5 使用参数特制化的效果
最下面这张图是使用了 adagrad 方法的效果,对不同参数采用不同的 lr,最后能到达loss 最低点.
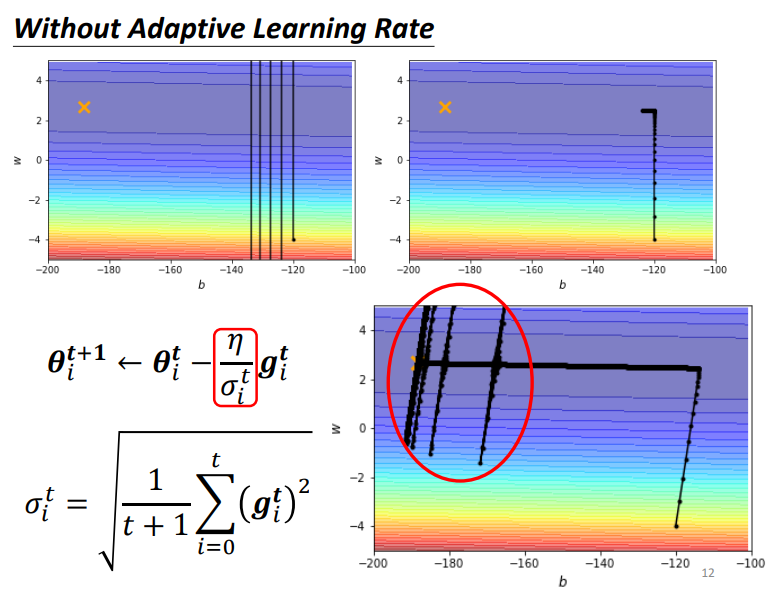
但是有个奇怪的现象,也就是在临近终点的时候出现了奇怪的上下不断移动.
为什么会产生喷发呢:在前面阶段,纵轴参数的 loss 的梯度都很大,而\(\sigma\)是计算以前的整体梯度,所以刚到达低谷的时候,\(\sigma\)还是很大的,新进步伐依旧很小,等在低谷走了一段后,在\(w\)轴方向累积了许多小的 g,导致\(\sigma\)变小,所以步伐就变大了,就会在某次更新时喷到很远.
请注意,上图是只列了一个参数的梯度,实际在画上面的\(loss\)图时,要看两个参数的梯度.
为什么走一段之后\(\sigma\)就变小了:因为\(\sigma\)的分子每次 + 很小的 g,而分母是 +1,分子加的比分母少,所以总体上\(\sigma\)是减小的.但后来喷射到比较远的地方,这些地方梯度比较大,\(\sigma\)又会增大,从而导致步伐变小,最后趋于稳定回到低谷.可以理解为摩擦力.但是累计一段时间还是会喷射.
1.6 如何解决累积导致的喷发问题
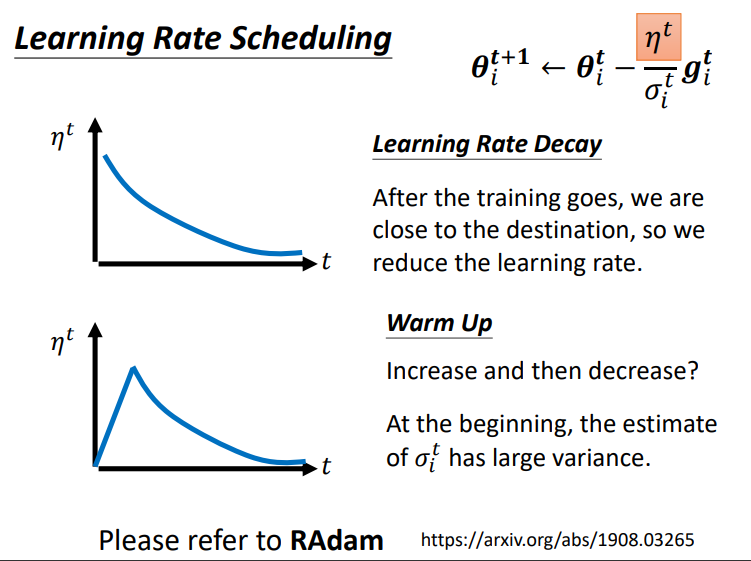
提出Learning Rate Scheduling.让 LearningRate 与 "训练时间" 有关.当\(\sigma\)在低谷中累积减小时,\(\eta\)也在慢慢减小,所以可以使得\(\frac{\eta}{\sigma}\)的整体变大趋势不明显,步伐也就不会太大导致喷发了.理想的情况是,随之训练的进行,会越来越接近目的地,所以我们希望 learning rate 能随着时间慢慢降低,从而使得在接近目的地时移动步伐能够缓慢前进,避免幅度太大导致出现抖动现象.
上面的方法就是经典的Learning Rate Decay,当然还有Warm Up的方法,即让LearningRate先上升再下降.这是一种黑科技,也不太能解释为什么这样做效果能好,不过普遍认为的原因是:在开始时\(\sigma\)搜集的数据不多(\(\sigma\)是过去梯度总结的结果),所以统计整体梯度不够有代表性,而刚开始的 lr 设置小点,能让\(\sigma\)搜集多点数据,统计出来的整体梯度就更精准更有代表性.
因此,我们需要将分子 \(\eta\) 也进行调整,将其升级为与时间相关的一个变量 \(\eta^t\)
2. 优化总结
针对优化我们有以下的tips,不只看当前梯度,还加上上一步方向的momentum,他主要考虑方向.加上\(\sigma\)对参数进行特制化,主要考虑大小.还能让\(\eta\)随时间变化.

(1) 使用动量,考虑过去梯度的 "大小" 与 "方向".
(2) 引入\(\sigma_i^t\),考虑过去梯度的 "大小" (RMSProp),不考虑方向.
(3) 使用 LearningRate Schedule,调整 \(\eta\) 让 LearningRate 与 "训练时间" 有关.
Adam可能是今天最常用的Optimizer,但除了Adam以外,还有各式各样的变形,但其实各式各样的变形大都三种模式,要么不同的方法算\(m_i^t\),要么不同的方法算\(σ_i^t\),要么采用不同的Learning Rate Scheduling的方式.

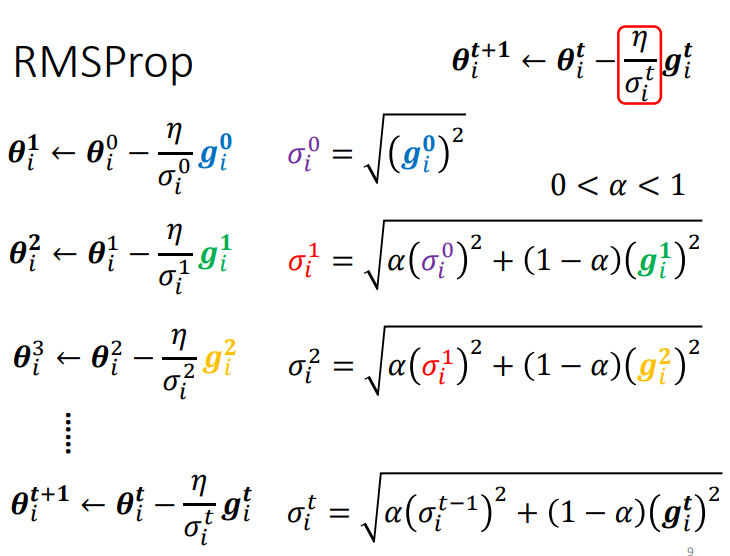

 浙公网安备 33010602011771号
浙公网安备 33010602011771号