2.2 类神经网路训练不起来怎么办 (二): 批次 (batch) 与动量 (momentum)
1. Batch(批次)
对抗临界点的两个方法就是batch 和 momentum
将一笔大型资料分若干批次计算 loss 和梯度,从而更新参数.每看完一个epoch就把这笔大型资料打乱(shuffle),然后重新分批次.这样能保证每个epoch中的 batch 资料不同,避免偶然性.
epoch是指将数据集分成batch后,将所有batch训练一遍,就是一个epoch
那么,为什么使用\(batch\)呢?
1.1 大小批次的运算时间对比
下图是两种\(batch\)的情况,第一种是\(full\) \(batch\),所有数据集都归于一个\(Batch\).第二种是极端的反面,一次只看一笔训练资料.

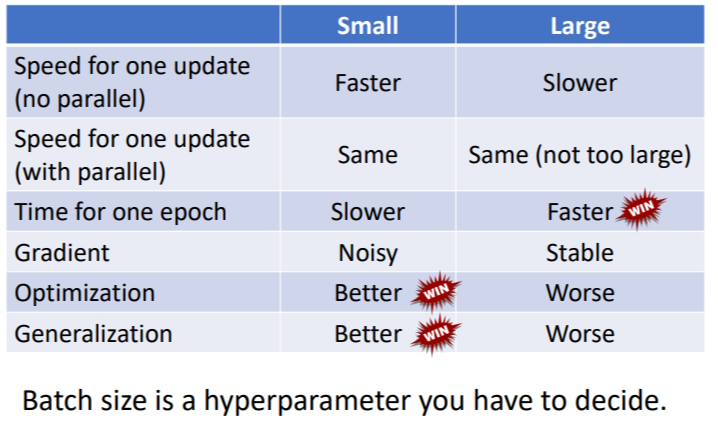
设大批次含有20笔资料,小批次含有1笔资料,那么大批次就是看完20笔资料后再更新参数,而小批次则是看1笔资料就更新一次参数,总共更新20次.我们可以看到大批次的单次运算时间长但效果好,小批次的单次运算时间短但效果差,需要运算多次效果才好.可以把大批次想象成迫击炮,小批次想象成加特林.
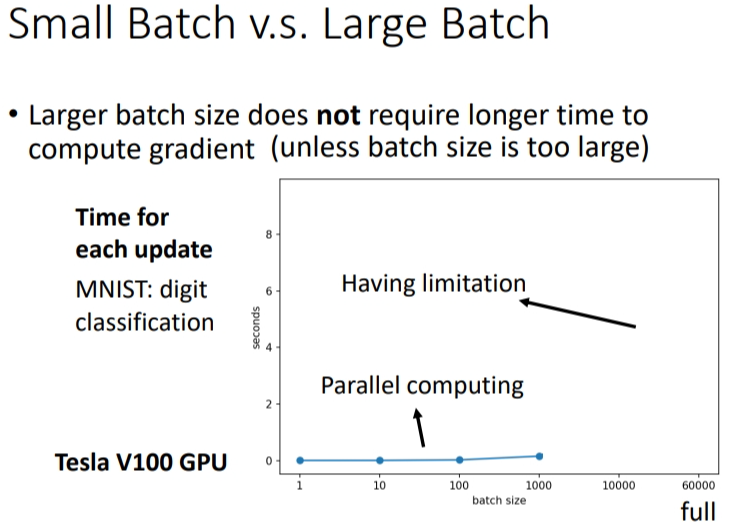
但是大批次时间长是没有考虑使用\(gpu\)(并行运算)的结果.如果采用GPU就可以做平行运算,从下图运算结果可以看出来:含有10笔资料和含有1000笔资料的批次,每次更新的运算时间差不多,但是含有的资料再增加,超过\(gpu\)的承受能力,运算时间就会急剧增加了.
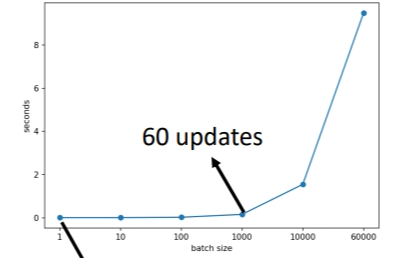
刚刚讲的运算时间是针对单次更新.而在1 个 epoch 中,小批次反而耗时更长,大批次耗时更短.原因是:同样是60000笔资料,小批次要更新60000次,而大批次只要更新60次,一次更新花费的时间又是差不多的,最后叠加起来肯定是大批次耗时更少.
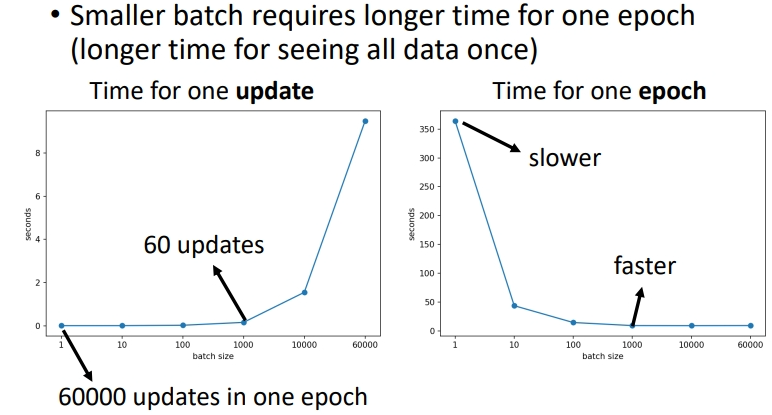
总结:没有平行运算时,单次更新大批次耗时更长;有平行运算时,单次更新大小批次耗时差不多,而 1 个 epoch中大批次耗时更短.

1.2 大小批次的性能对比
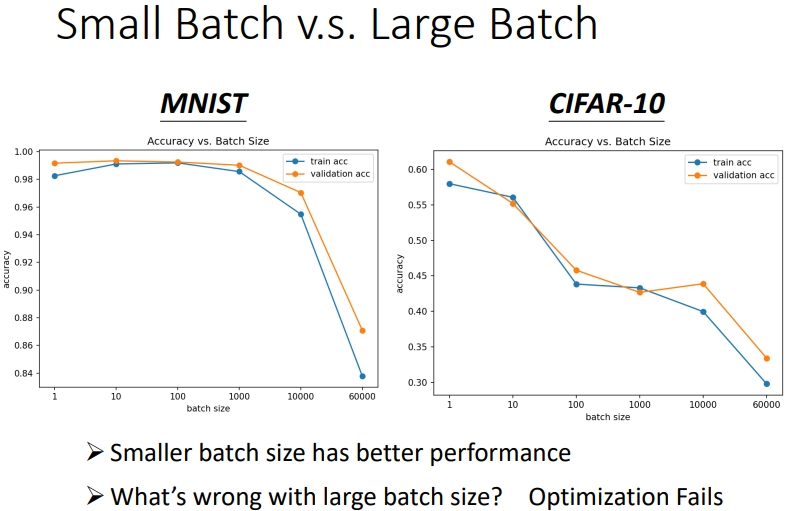
小批次有更好的性能.由图可知同一个模型,同一个网络,\(training\)误差随着\(batch\) \(size\)的增大而增大,\(testing\)的误差也是.如果是 model bias 的问题,那么在 size 小的时候也会表现差,而不会等到 size 变大才差.同样也不是过拟合问题,因为在这张图上并没有改变模型,按道理模型能表示的function space是一样的.所以这是Optimization issue(优化问题)导致大批次性能差.
1.2.1 为什么small batch训练结果会比较好
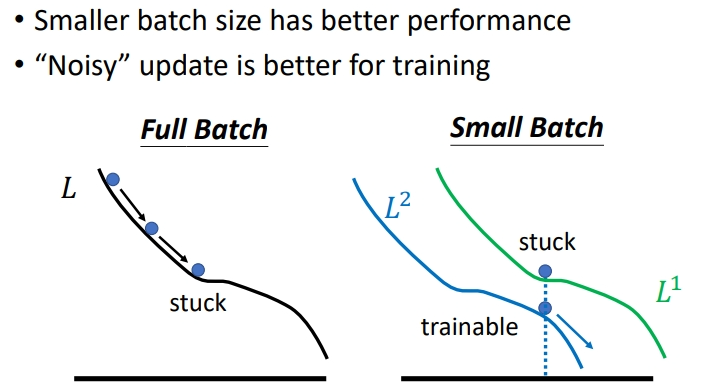
每次更新的时候,用的\(loss\)函数会有差异(如右图),因为不同的 batch 用不同的 loss function.换了个 loss 函数就更不容易卡住.
个人理解:我们绿色那条线是根据第一个Batch作的loss曲线,那么参数的更新方向也是根据第一个\(batch\)的数据更新.当运行到第二个batch时,数据点变化了,曲线也就变化了,所以当前参数在曲线上的位置也变化了.
1.2.2 为什么small batch测试结果会比较好
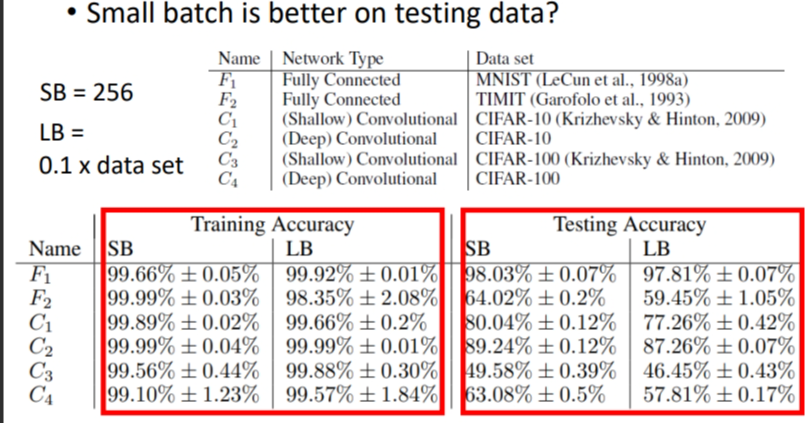
那这边还有另外一个更神奇的事情,其实小的 Batch 也对 Testing 有帮助.
data set的大小是60000.上面的例子在Traning和Testing是一起下降,而这里不一样.红框框中可以看出在训练时 SB(小批次)和 LB(大批次)的准确率都高,但是在testing 时,SB的准确率还是比较高,而LB的准确率则更差点,此时 LB面临的问题是overfitting.
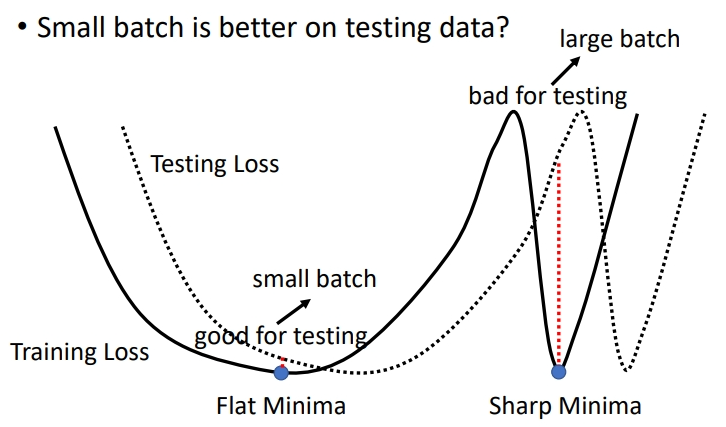
那么为什么会有这种测试集过拟合的现象?有一个猜想如下(还没有试验证明的).
训练和测试时的数据分布有差异,所以两者的 loss 也有差异(如下图).小批次是在平滑的最低点,大批次是在陡峭的最低点,只要 testing loss 有一点变化,陡峭处就会发生大变化,从而导致大批次在测试时表现不好.
至于为什么大批次会让模型走到陡峭的最低点,这是很多人的说法,直觉是小batch很容易变动,陡峭的最低点没有办法困住小batch,而平原上的最低点才有可能困住小batch,还没有证明.
总结:小批次在 1 个 epoch 中的速度很慢,耗时很长,但是小批次在优化过程性能更好,在测试时的性能也更好.而批次大小是一个超参数,需要自行设定.
2. Momentum(动量)
2.1 Momentum如何使用在梯度下降中
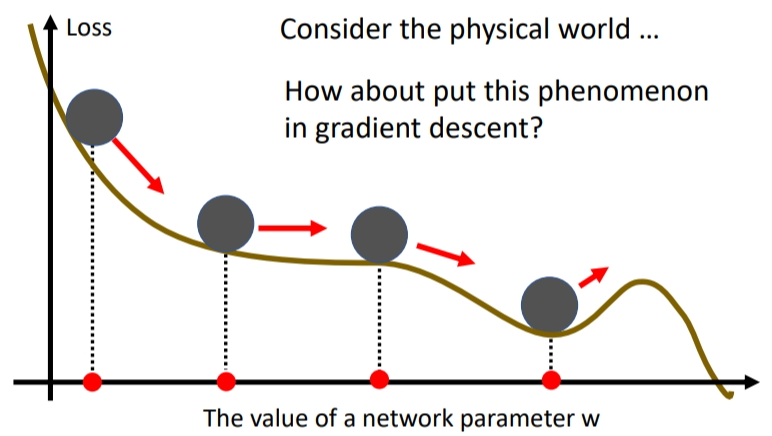
在物理中,重物借用惯性,能够滚得更远.将这种思想应用于梯度下降中,用这种思想能使参数越过临界点!!
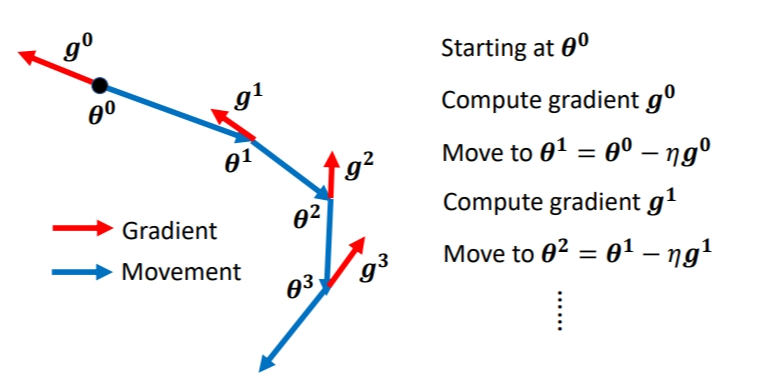
我们先复习一下原来的Gradient Descent是怎么运作的.即往梯度移动的反方向更新参数.
- 特点:在更新现在的梯度下降方向的时候,每一次仅利用前一次的梯度下降方向.
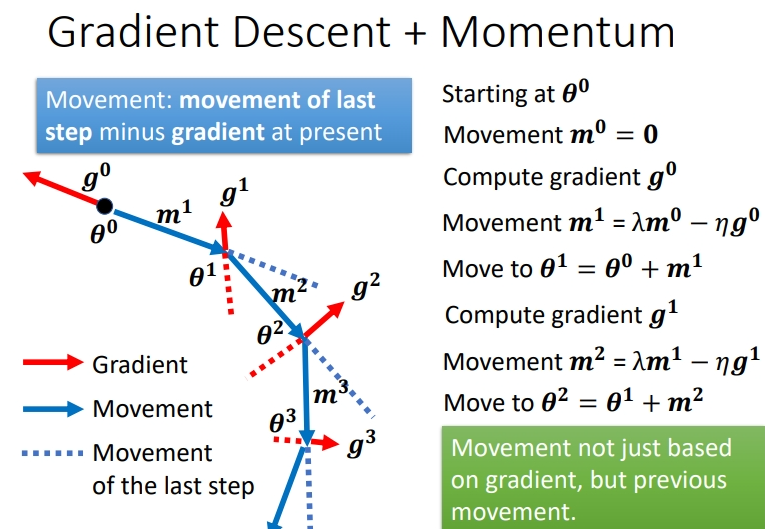
而 momentum 则是在gradient 的反方向上加上上一步的方向(在式子中用 m表示),这两个方向是向量相加,用平行四边形法则.上一步的方向就相当于惯性力量. - 在更新现在的梯度下降方向的时候,考虑在此之前计算过的所有的梯度下降方向.注意看图,下一次下降方法考虑了上一次的方向和本次梯度下降方向,取了两者的折中.
2.2 另一种解读方式
m 是前面所有gradient 的综合,只不过乘上了不同的系数.注意\(\lambda\)也是一个参数和\(lr\)一样需要调整.这就是不同的解读方式,可以看作考虑了所有梯度下降的方向.

2.3 如何理解动量可以帮助解决局部最小值问题
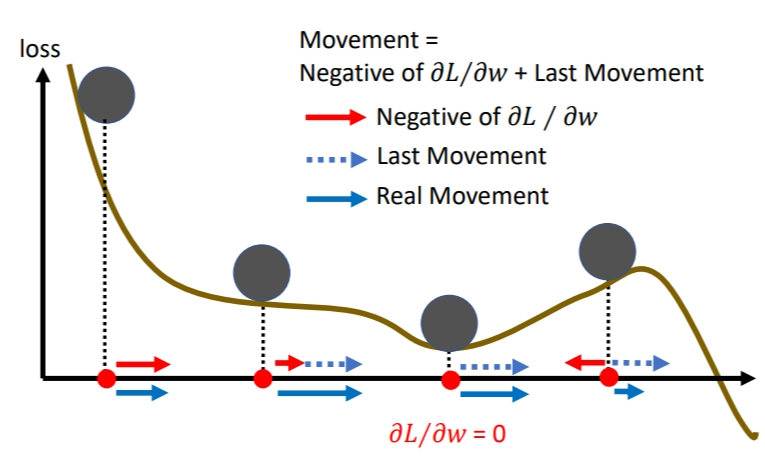
当我们考虑了动量,方向变成了梯度更新产生的距离和上一步产生的惯性距离之和.第三个球位于临界点,梯度更新产生的距离虽然是\(0\),但是还有上一步惯性距离,所以球能越过临界点,假如第四个球的上一步惯性距离大于梯度距离,则球可能可以越过山顶.
3. 总结
临界点的梯度为零.临界点可能是局部最小值或者鞍点:可通过 H矩阵判断临界点是哪一个,假如通过 H矩阵判断出是鞍点,那么可以沿着 H矩阵的负的特征向量方向更新参数,从而逃离鞍点.从试验中得知局部最小值很少存在.
小批次和动量能够帮助鞍点.