选修-3-Gradient Descent
1. Review:梯度下降法
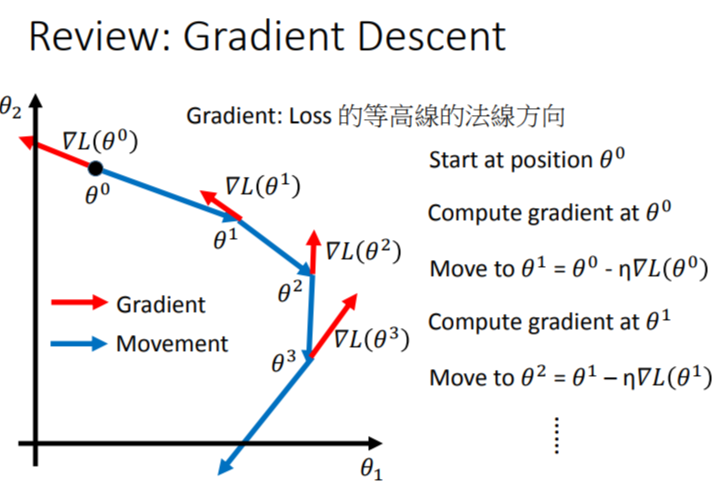
我们建立一个模型,需要为这个模型找到一组参数,这个参数可以最小化\(Loss\).我们使用梯度下降法来找到这个参数.注意,下图的\(▽L\)就是梯度.

梯度下降以可视化表现如下:
2. 梯度下降的tips
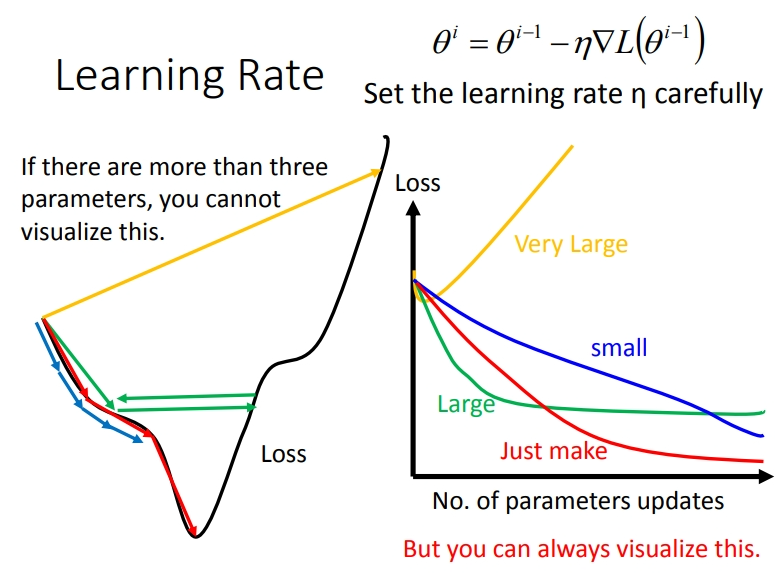
2.1 小心调整lr
学习率控制梯度下降速度.
2.1.1 自适应学习率
学习率的调整是很麻烦的,但也有一些\(ideas\),在初始的时候,离局部最小点比较远,此时的学习率会比较大,但随着\(epochs\)进行,学习率会逐渐减小.比如设置成\(\eta^t = \frac{\eta}{\sqrt{t+1}}\).但这只是一种情况,最好的情况是每个不同的参数都给予不同的学习率.

2.1.2 Adagrad
这个算法让每个参数的学习率都把它除上之前微分的均方根.
-
对于普通的梯度下降,我们要控制它的学习率,可能会这样做:

-
但Adagrad可以做得更好:

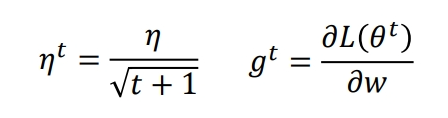
那么之前微分的均方根到底是什么意思呢?举个例子就明白了.请注意\(\eta\)的式子就是上面的式子,同理\(g\).

总结一下,就是下面这个式子:

这只是Adagrad算法的其中之一的方法,还有很多属于Adagrad的算法,比如大名鼎鼎的\(Adam\)算法.
2.1.3 Adagrad存在的矛盾
在\(Adagrad\)中,当梯度越大时,步伐应该越大,但是分母又导致当梯度越大的时候,步伐越小.
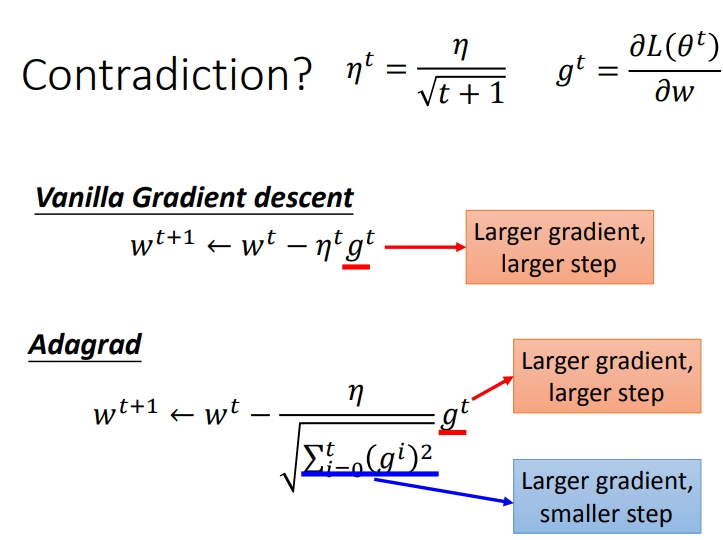
有\(paper\)给了直观解释,我个人有点理解不了为什么给予这种反差,这是一位\(po\)主的笔记.
\(update\):把\(\frac{\eta}{\sqrt{\sum_{i=0}^{t}(g^i)^2}}\)看作学习率的话,如果前四格\(grad\)一直很小,\(lr\)就会适当增大.如果\(grad\)一直很大,那么\(lr\)就会适当减小.这是弹幕的解释.


李宏毅老师也给了自己的解释.下面是其他博主对李老师观点的总结,最好的步伐与该点的梯度成正比,当梯度越大,说明这个点与最低点也越远:

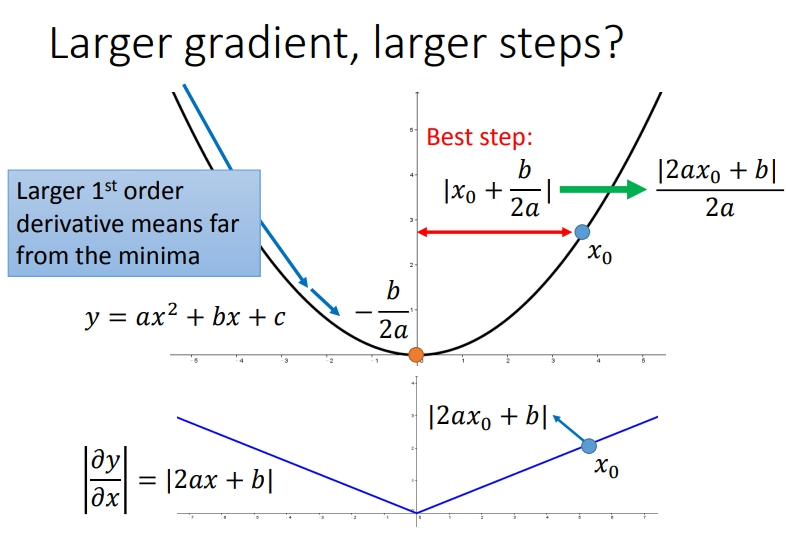
考虑多个参数的时候,情况又是不同的.从下图是两个参数与Loss之间的关系图.
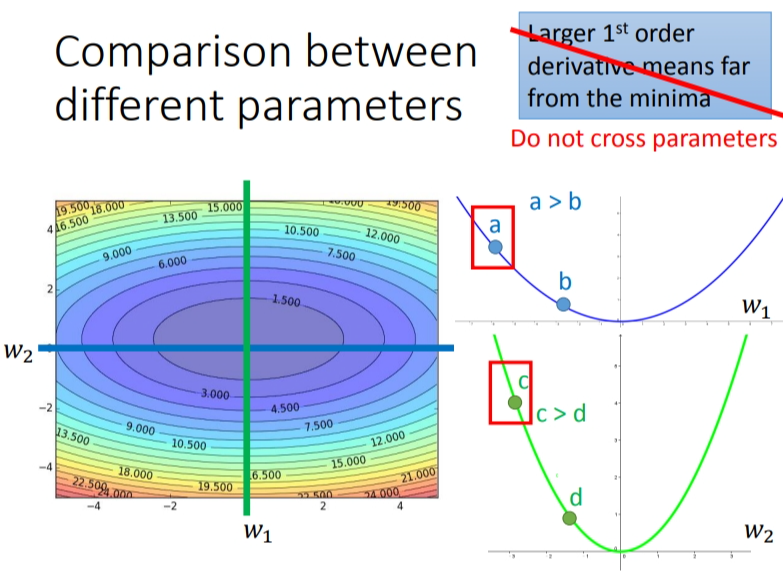
如果我们只考虑\(w_1\),也就是只看蓝色那条线,那么\(a\)的梯度大于\(b\)的梯度,\(a\)离最低点越远.同理绿色那条线.但如果我们对比\(a\)对\(w_1\)的微分,\(c\)对\(w_2\)的微分,这个结论又不成立了.但如果我要考虑多个参数,到底应该怎么想呢?
前面我们得到的最佳距离\(\frac{2ax_0+b}{2a}\),还有个分母\(2a\),对\(function\)进行二次微分刚好可以得到:
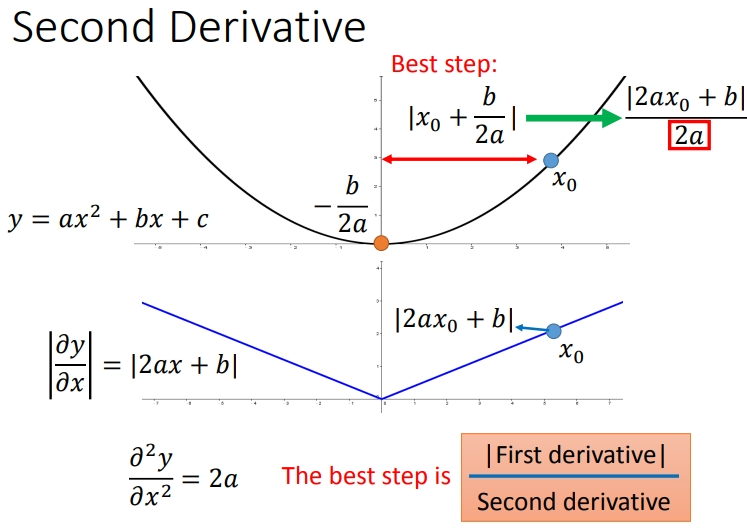
所以最好的\(step\)应该将二次微分考虑进来.我们继续看上上图的蓝线,可以发现蓝线的二次微分比较小,而绿线的二次微分比较大.因此比较一次微分是不够的,需要一起考虑.
2.1.4 Adagrad进一步解释
前面篇幅介绍的与矛盾有什么关系呢?我们用上面函数计算出\(best\) \(step\)是一次微分和二次微分的分式.实际下面的分母就是在不增加计算成本的情况下,尽可能去估测二次微分的值.为什么这样可以预估呢?下图的折线是一次微分的变化图像,\(\sqrt{\sum_{i=0}^{t}(g^i)^2}\)实际类似于在一维微分图像上取样点,绿线取到一次微分值大的点比较多,因此\(\sqrt{\sum_{i=0}^{t}(g^i)^2}\)的值求平均就会比蓝线大,从而反映二次微分的大小(不是近似).
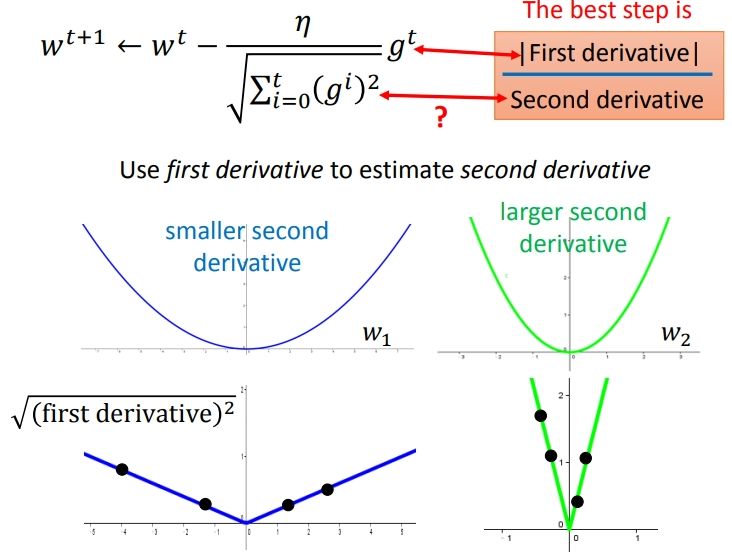
从这里到上面讲的都是为什么要这样构造\(\frac{\eta}{\sqrt{\sum_{i=0}^{t}(g^i)^2}}g^i\),个人感觉get不到和前面矛盾的关系
2.2 Stochastic Gradicent Descent
我们在之前的计算梯度下降中,\(Loss\)的计算是基于所有样本,然后再算梯度.而随机梯度下降先只拿一个样本出来,然后计算它的\(Loss\),再根据这个样本\(Loss\)计算梯度.也就是说一般的梯度下降,我们求梯度的时候,它的\(Loss\)是所有样本的\(loss\)式子和,再针对式子和求导.而随机梯度下降,只看一个样本的\(Loss\)就求导.

下图是两种方法的对比.常规的梯度下降算法走一步要处理二十个\(example\),但随机算法此时已经走了二十步(每处理一个\(example\)就更新)

2.3 Feature Scaling
当模型的特征分布很不一样时,我们就会考虑做\(Scaling\).

那么为什么要这样呢?举个例子,见下图:
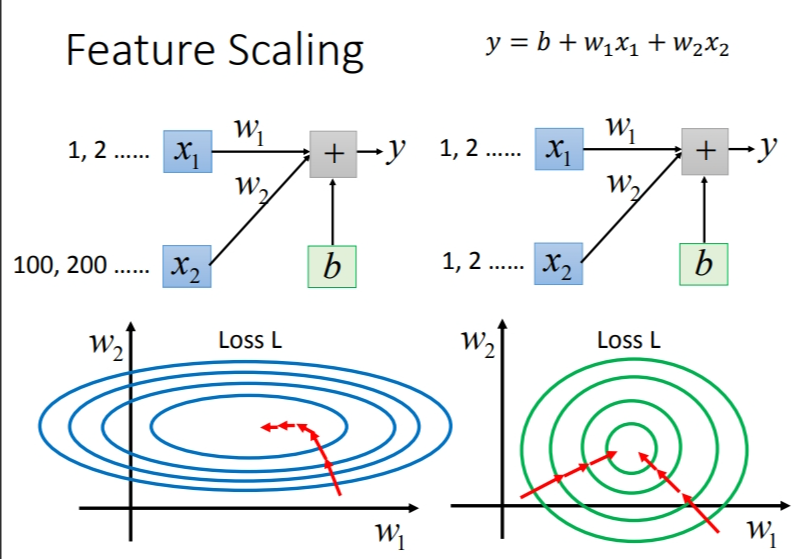
如果我们的\(x_2\)都比较大的话,那么\(w_2\)变化就会对\(Loss\)影响很大.它们与\(Loss\)的变化见上图蓝色部分.\(w_1\)变化影响比较小,所以当\(w_2\)不变时,它的微分曲线比较平滑..但\(x_1\)和\(x_2\)差不多的话,它们与\(Loss\)的变化见上图绿色部分.
那么,这个对\(Gradicent\) \(Descent\)有什么影响呢?当参数与\(Loss\)的图像是椭圆形时,对于不同的参数,可能就需要不同的学习率,才能移动到局部最低点.


2.3.1 怎么做Feature Scaling
方法有很多,比较常见的方法就是利用平均值和标准差对绿色框的数值做归一化:
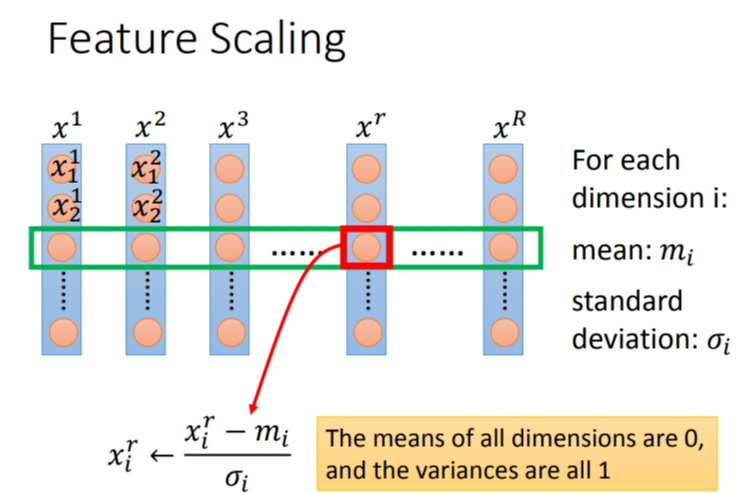

这实际是将每一个参数都归一化为标准正态分布.

3. Gradient Descent的理论基础
我们在参数与\(Loss\)的图像上,瞬间找到最低点是不大可能的.但是如果先给予我们一个点,再限定一个范围,找该范围的最低点会更加容易.
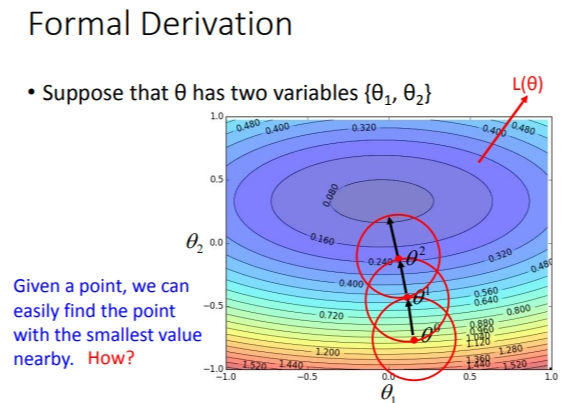
那么怎么在限定范围内找到最低点呢?首先来看一个理论,如果\(h(x)\)在\(x=x_0\)处无限次可微,那么\(h(x_0)\)可以用泰勒展开为:

但是,当\(x\)很接近\(x_0\),\(x-x_0\)会远大于\((x-x_0)^2\)、\((x-x_0)^3\),所以后面的可以省略掉.
上面是单参数泰勒展开,当然也存在多参数的情况.

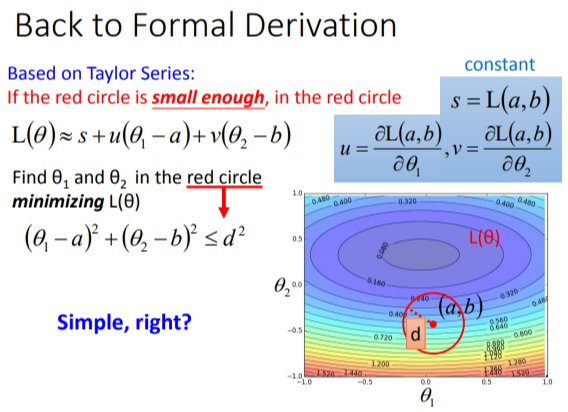
我们将泰勒展开应用在Gradicent Descent上.红线的足够小类似于上面的当\(x\)很接近\(x_0\)的情况.这样\(L(\theta)\)就可以简化为简单的式子.

问题就变成了,\(\theta_1\)和\(\theta_2\)在圆心为\((a,b)\)内移动.然后求\(\theta_1\)和\(\theta_2\)的取值,让\(L(\theta)\)最小.
这样的问题可以转为向量的\(inner\) \(product\).\(L(\theta)\)是\((u,v)\)和\(\theta\)的内积.参考内积公式,可以得出当\(\theta\)和\((u,v)\)完全反方向时,得到的值最小.

请注意一下,仅仅反方向不是最小,最小还是需要用一个\(scale\)将向量的长度调整到弧线处.

这样我们就求到了\(\theta_1\)和\(\theta_2\)最合适的值.再将原来的\(u,v\)代回去.我们可以发现带回去的这个式子,就是Gradient Descent.但是成立的前提是\(L(\theta)\)的展开要成立.同时,\(\eta\)的大小需要让长度不能超过红圈,这代表学习率也不能太大.

也可以对泰勒展开到二次式、三次式等等,但是这种计算对\(deep\) \(learning\)来说成本太大.
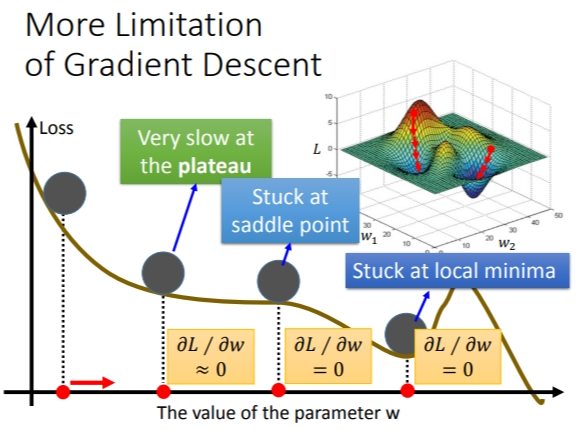
4. Gradient Descent的限制

\(saddle\) \(point\)就是鞍点,一级微分\(=0\),但是左右导数符号相同.