选修-2-Where does the error come from?

CLICK,这个写得更好.

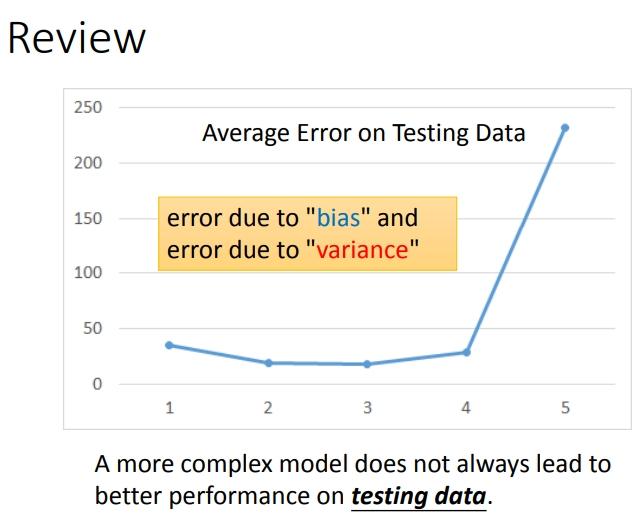
1. Error的来源

  error实际来源于bias和variance.

2. Estimator

  我们用回归模型预测宝可梦的战斗力时,是不知道宝可梦实际计算函数的,我们只能使用自己估测的函数去尽可能靠近这个函数.

  那么一个Estimator的bias和variance是指什么呢?以概率与统计来说明:

  假设预测一个变量的均值和方差.直接预测是不可能的,所以取\(N\)个样本点.\(N\)个样本点的均值\(m\)只有在\(Sample\)无穷多个点时,(大概率)才会与\(\mu\)相同.我们进行多次实验\(Sample\),每次\(m\)都不同.但如果我们算\(m\)的期望值,这个值会恰好是\(\mu\).
  每次实验计算\(m\)都与实际\(\mu\)有偏差,这个偏差大小取决于\(\sigma^2\).

  我们用\(m\)计算\(s^2\)来估测\(\sigma^2\).注意右边的\(s_i\)都是\(s_i^2\),图里没标.\(s^2\)是一次采集的样本方差,\(\sigma^2\)是实际方差,这两关系如下.

  variance和bias的意义可以用打靶来类比,一次实验得出的函数是\(f^*\),多次实验求期望得到的函数是\(f^-\),实际准确的函数是\(\hat{f}\):

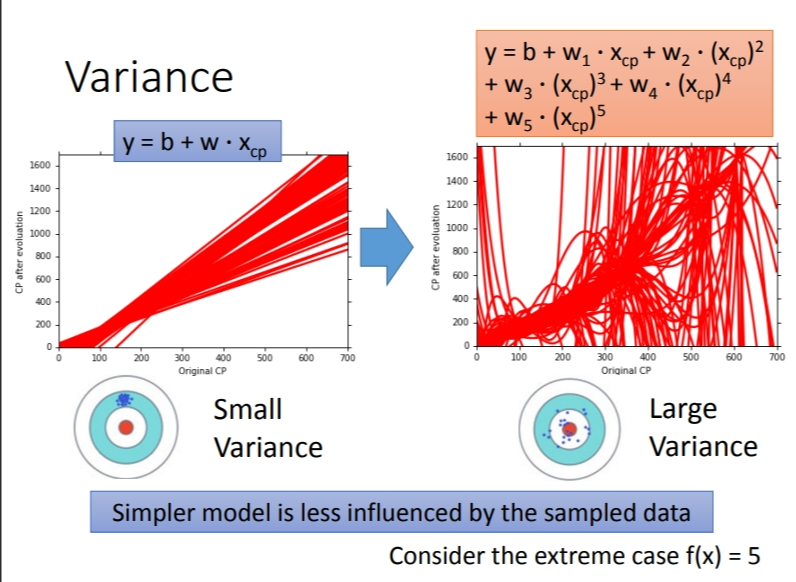
2.1 考虑不同模型的方差

  一次模型的方差就比较小的，也就是比较集中，离散程度小。而5次模型的方差就比较大，同理散布比较广，离散程度较大。所以用比较简单的模型，方差是比较小的（就像是射击的时候，每次射击都集中在一个比较小的区域内）。如果用了复杂的模型，方差就很大，分散就比较开。这也是因为简单的模型受到不同训练集的影响是比较小的。

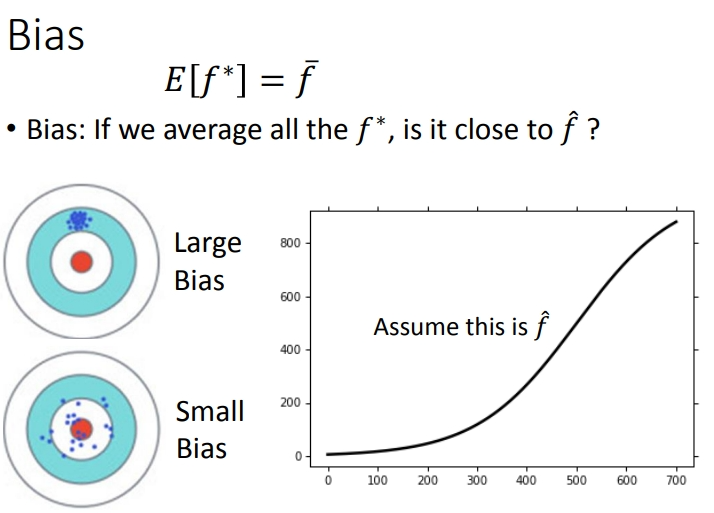
2.2 考虑不同模型的偏差

  一次模型的偏差较大,而复杂的\(5\)次模型,偏差较小.简单的模型函数集的\(space\)比较小，所以可能\(space\)里面就没有包含靶心,肯定射不中，而复杂的模型函数集的\(space\)比较大,可能就包含靶心,只是没有办法找到确切的靶心在哪,但是足够多了,就能找到真正的\(f\)

  下图是一次式,三次式,五次式分别做五次实验的情况.

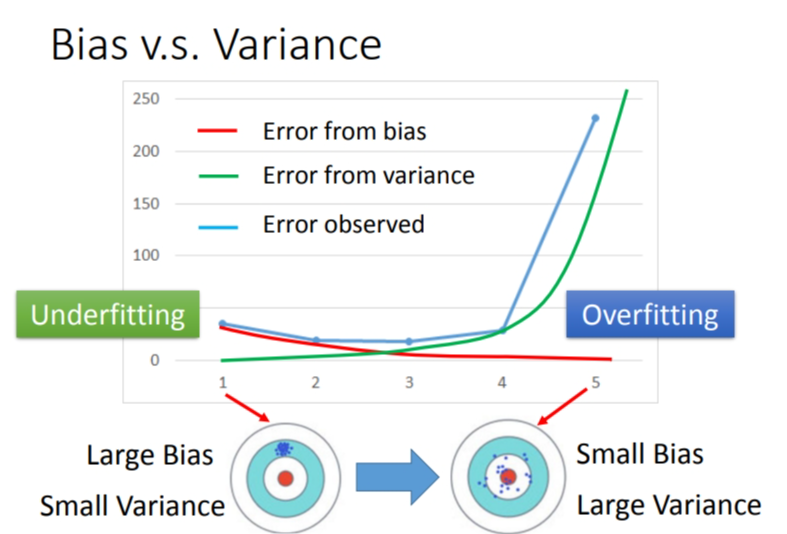
2.3 偏差 vs 方差

  简单模型(左边)是偏差比较大造成的误差,这种情况叫做欠拟合,而复杂模型(右边)是方差过大造成的误差,这种情况叫做过拟合.偏差小表示瞄地准,方差小表示射击稳定.

3. 怎么判断高偏差和高方差

  如果模型没有很好的训练训练集,就是偏差过大,也就是欠拟合.如果模型很好的训练训练集,即再训练集上得到很小的错误,但在测试集上得到大的错误,这意味着模型可能是方差比较大,就是过拟合.对于欠拟合和过拟合,是用不同的方式来处理的.

3.1 怎么处理欠拟合

  这个时候就要重新设计模型,因为之前的函数里面可能根本没有包含\(\hat{f}\).可以：将更多的特征加进去，比如考虑高度重量等，或者考虑更多次幂，使用更加复杂的模型。

3.2 怎么处理过拟合

  最简单的方法就是，增加更多的数据，但是很多时候不一定能做到收集更多的data。可以针对对问题的理解对数据集做调整。比如识别手写数字的时候，偏转角度的数据集不够，那就将正常的数据集左转15度，右转15度，类似这样的处理。

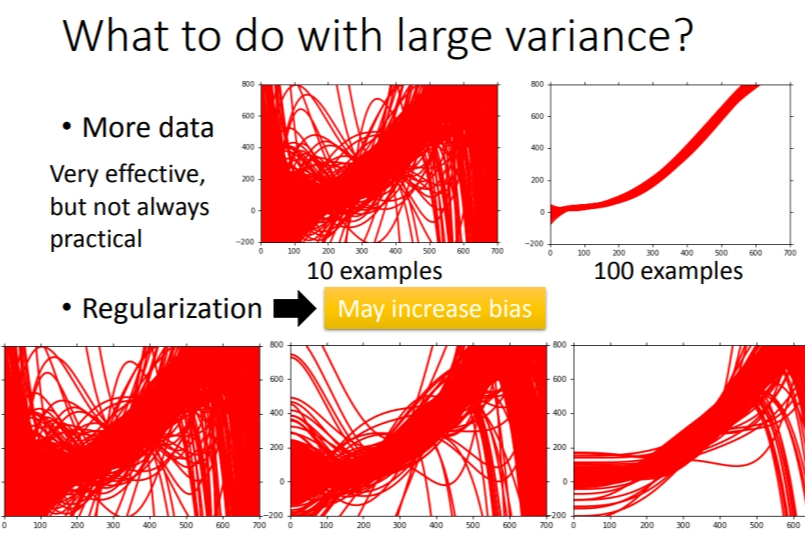
  其次就是正则化,增加惩罚项.让曲线更加平滑(平滑的意思是曲线波折没有那么多,受数据影响比较小)

4. 模型选择

  在\(bias\)和\(variance\)之间需要一个平衡,平衡\(bias\)和\(variance\)产生的错误,使得总错误最小.但是我们不能盲目的选择不同的训练集训练不同的模型,然后在测试集上比较错误,模型的错误小,就认为该模型效果好.

4.1 交叉验证

  我们做老师布置的作业的时候,\(public\)测试集是已有的,\(private\)是没有的.交叉验证就是将训练集再分为两部分,一部分作为训练集,一部分作为验证集.用训练集训练模型,然后再验证集上比较,确认最好的模型(也就是用验证集选择\(model\)).之后,再用全部的训练集训练模型,然后在再用\(public\)的测试集进行测试,此时一般得到的错误大些.但是不我们不建议再回去调整参数,让在模型在\(public\)的测试集上的效果更好.

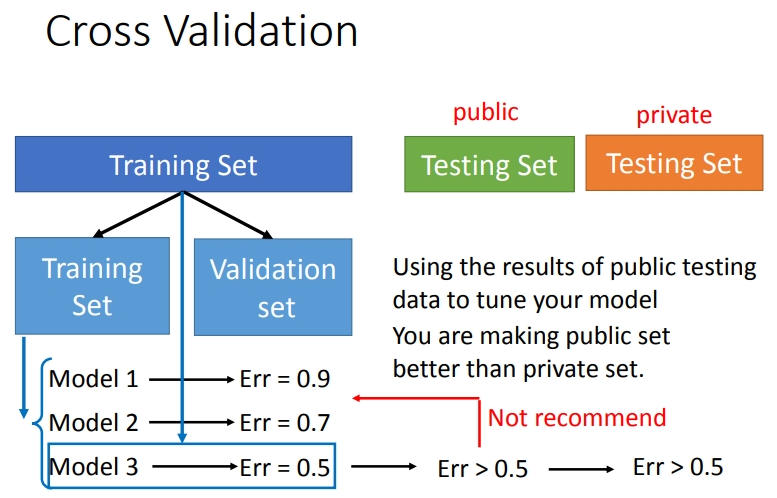
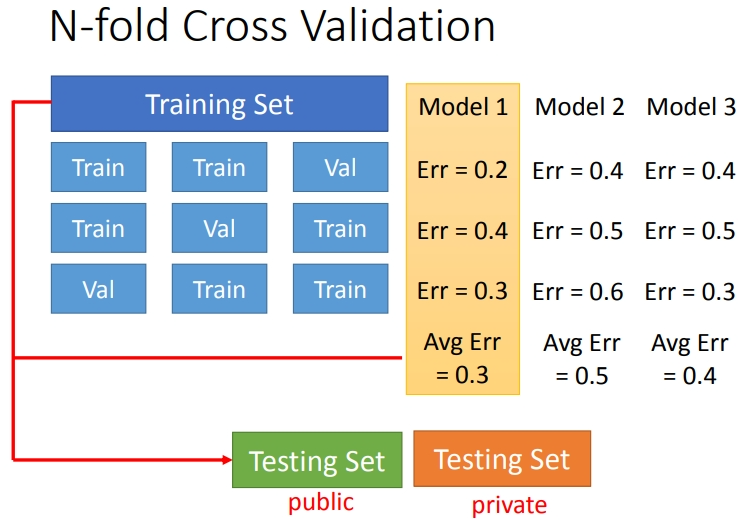
4.2 N折交叉验证

  上述方法可能会担心将训练集拆分的时候分的效果比较差,那么可以用下面的方法,也就是多做几次切分训练集.
  将训练集分成\(N\)份,比如分成\(3\)份,然后在三份中训练结果\(Average\)错误是模型1最好,然后全部训练集训练模型1.