选修-1-预测宝可梦与分类宝可梦-李宏毅
个人建议看这个Click和这个Click.第二个链接解释了生成模型.
啥都会一点的研究生在B站的视频是乱的,但这也不能怪\(up\),因为李老师给的顺序就是乱的,我个人感觉应该先看选修再看主修,选修是youtobe上17年的视频,那个顺序是正常的.
1. Regression
下图是线性回归的应用,比如预测股市、无人车驾驶预测方向角度、推荐系统.

1.1 线性回归的例子
线性回归举得是根据原来的宝可梦基础数值预测进化后宝可梦的战斗力的例子.

要想预测必须先建立model,再找到好的参数.

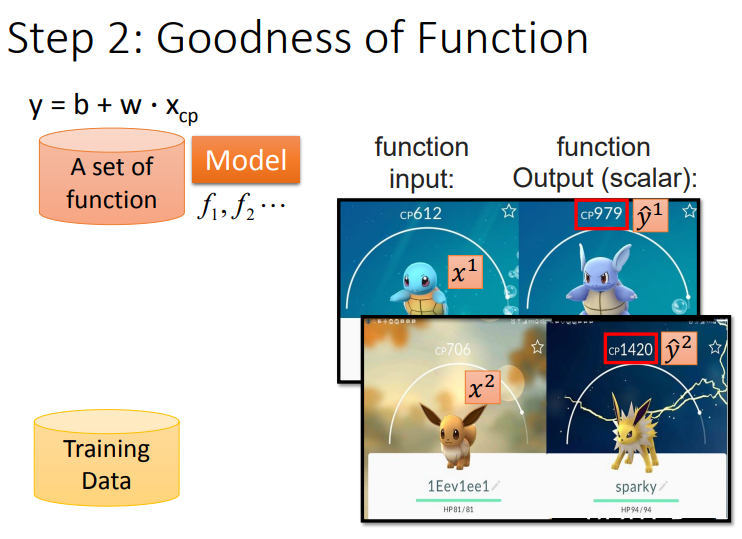
其次定义Loss Functoin.

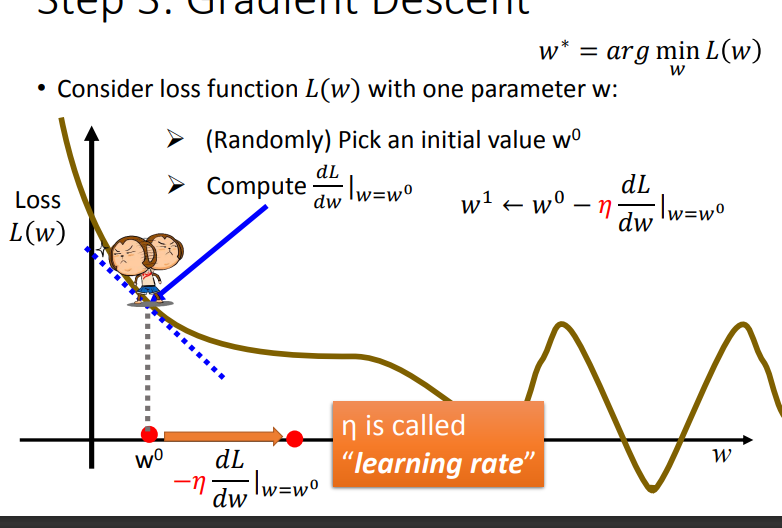
利用梯度下降减小\(Loss\).可以很容易发现梯度下降容易陷入局部最优.但是,当Loss Function定义为凸函数(\(convex\))时,就不存在局部最优解,这是凸函数的一个特性.线性回归的损失函数MSE(Mean Squared Error)平方均值误差是凸函数,这是线性回归不存在局部最优解的原因.

当我们使用一次函数作为模型的函数时,可以发现在测试集上效果不理想.

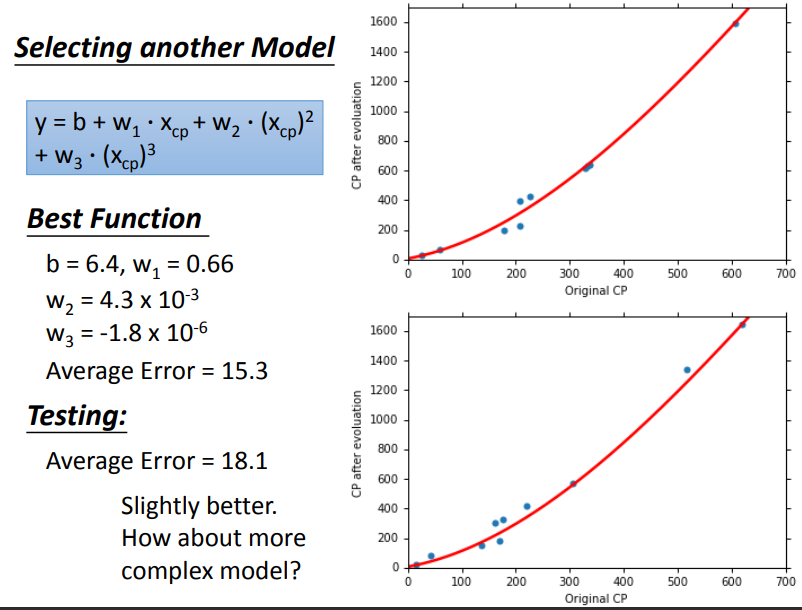
当使用二次函数时,效果变得更好了.

使用三次函数,效果变化不是很大.但四次项,效果就下降了.这就是过拟合现象.
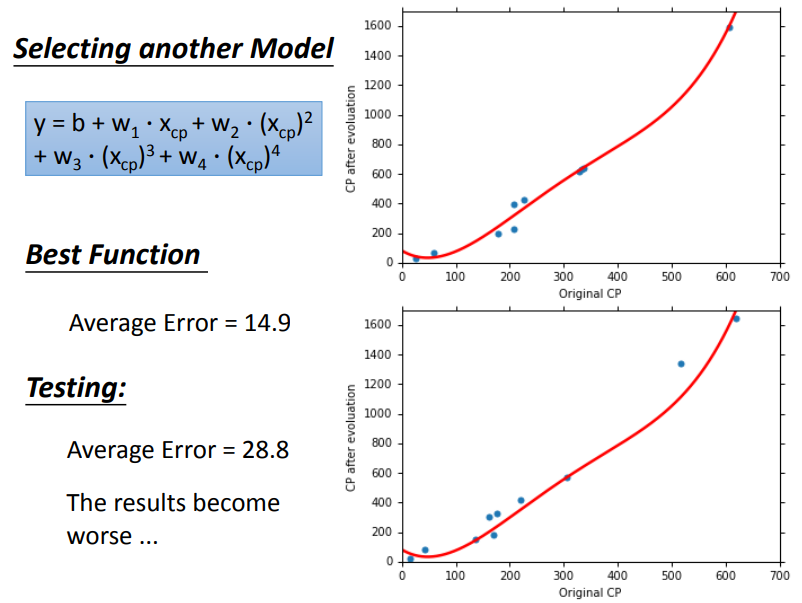
为了提高效果,设计了一个新的模型,这个模型考虑了种类,\(\delta\)x_{cp},可以看作特征,因此也算线性模型.


如果模拟过拟合了,可以使用正则化的方法.正则化可以使得模型对输入的变化不那么敏感.因为正常的数据有可能被噪音干扰导致变化.顺带一提,正则化不会对偏置进行惩罚.因为它不影响模型的平滑程度(模型过于平滑图像会变成直线,不平滑会过拟合,\(bias\)只会影响\(function\)的上下移动)

2. Classification
机器学习用于分类就是模型输入一个\(x\),输出一个\(Class\)类别.
这个\(x\)是宝可梦的矢量表示,我们会抽取宝可梦的一些特征,然后将特征组成一个向量,宝可梦用向量表示.

首先要阐明的是,分类问题不适合用回归模型来做,因为回归模型会惩罚那些过于正确的预测.而且在多分类上,如果我们用1映射类别1,2映射类别2....就表示那些相近的类别存在某种关系,但实际上是不存在的.
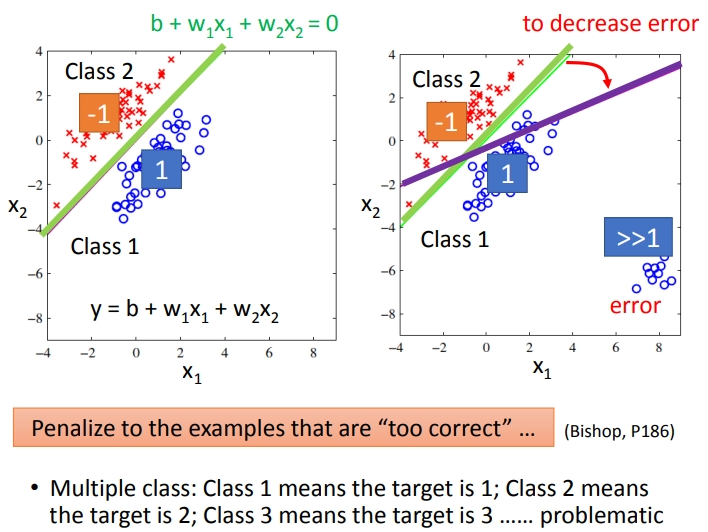
对于分类模型,更理想的方式是输入向量,然后模型的输出是离散的.

对于这种模型的实现有多种方法,下面只是提出其中一种,使用概率计算宝可梦的分类:

以具体例子来说,我们构建一个分类水系和一般系的模型,在宝可梦图鉴里,前400大概有79只水系,61只一般系.从下面的图可以看见,我们要计算\(P(C_{i})\)还是很好计算的.但是我们还需要计算\(P(x|C_1)\)


只考虑宝可梦的特攻和特防,画成二维图观察.假设下图分布是符合高斯分布(正态分布)的,那么我们就可以就训练集的数据计算新出现的水系宝可梦从水系集合里抽出来的概率.
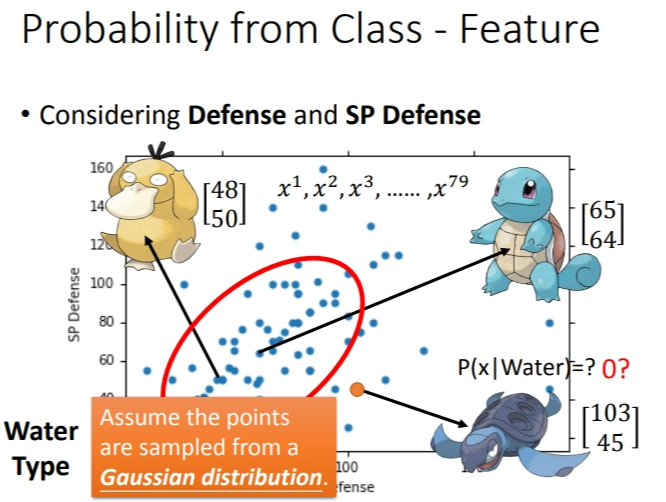
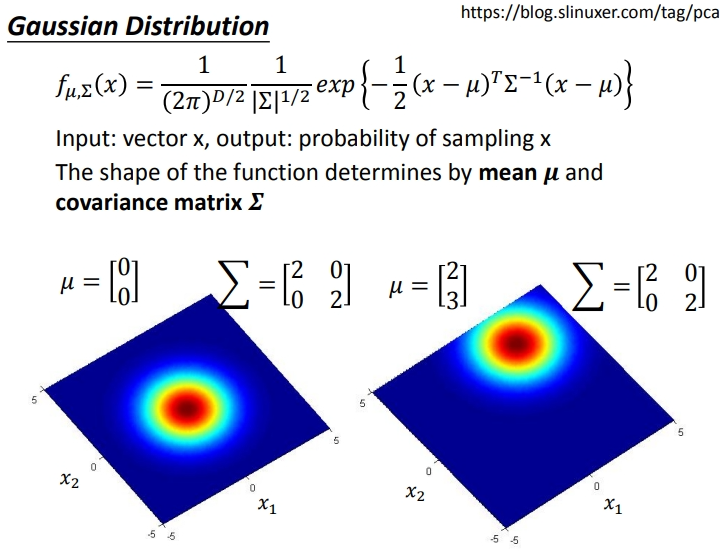

&esmp;接下来就找一个正态分布函数,这个正态分布函数随机出这79个点(训练集)的概率是最大的.再用这个函数预测新样本的概率.

从直觉来看,显然用这79个宝可梦的均值和方差构成的正态分布函数是符合我们需求的.


通过计算\(P(x|C_1)\)和\(P(x|C_2)\),就可以按下面公式计算模型对新数据的预测.

实际取一个阈值作为分类的分界线.可以发现如果只采用两个特征,测试集正确率只有47%.而如果采用7个特征,测试集准确率大概有54%.这也的准确率还是很低,那么怎么修改模型?

2.1 修改模型
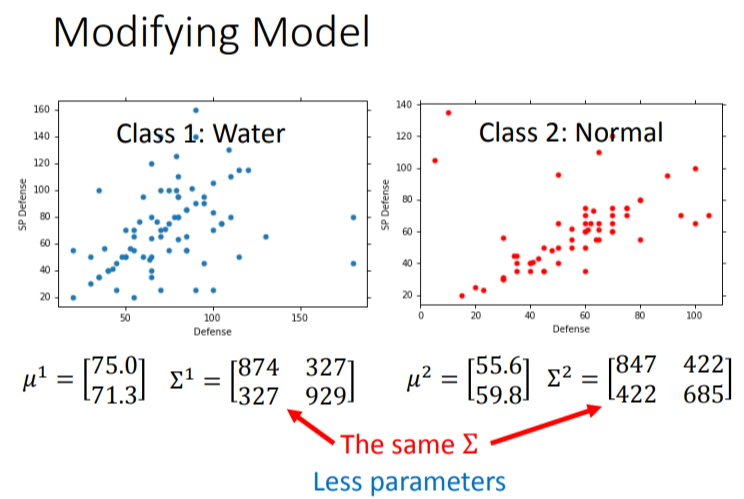
在前一个模型里,我们给每个类都构建了一个高斯函数,但实际上为了避免过拟合,即减少参数,我们可以让不同类共享同一个covariance matrix.
通常来说,不会给每个高斯分布都计算出一套不同的最大似然估计,协方差矩阵是和输入feature大小的平方成正比,所以当feature很大的时候,协方差矩阵是可以增长很快的。此时考虑到model参数过多,容易Overfitting,为了有效减少参数,给描述这两个类别的高斯分布相同的协方差矩阵。


2.2 建模三部曲
实际建立模型也分为三步,我们是使用上面的高斯模型计算\(P(x|C_1)\)等,对\(P(x|C_2)\)又采用不同的高斯模型.再利用Loss function和优化器找到最佳的模型参数.模型参数实际上就是高斯函数里面的均值和协方差.

2.3 概率分布
前面用于计算\(P(x|C_i)\)的使用了正态分布,实际上也可以使用其他分布.我们将宝可梦映射为一个向量,如果向量每个特征是彼此独立的,那么可以得到下面的公式,转化为一维高斯分布连乘的问题.这实际是朴素贝叶斯模型.

2.4 Posterior Probability
我们把后验概率的式子展开,可以变成熟悉的激活函数\(sigmoid\).

可以推导一下\(Z\)到底是什么.



最后推导\(z\)等于下图,但如果我们假设\(\Sigma\)是共用的,那么又可以消掉一些项.最后我们可以将\(P(C_1|x)\)转化为简单的式子.



