1.Introduction of Deep Learning - 李宏毅
先附上链接,看过吴恩达的感觉很多没必要复述了.
this 和 that
hyperparameter:超参数,需要自己设定的参数,来调整跨越步伐的大小.domain knowledge:对手头这个问题的理解,利用一切可用的信息,从各种角度各种先验知识去建一个最适合当前问题的model ——来自知乎
2. 深度学习基本概念简介
2.1 如何表示更为复杂的模型
在上一节介绍的线性模型只能表示线性的情况,但生活中的很多事物是无法用线性表示的.因此需要更为复杂的模型.
2.1.1 连续曲线
最有弹性的模型就是连续曲线,因为它描述复杂问题最为精准!!在高数里面我们就学过,用线段去逼**滑的曲线,这里的思想也是如此:充足的分段线性曲线可以逼*连续曲线!
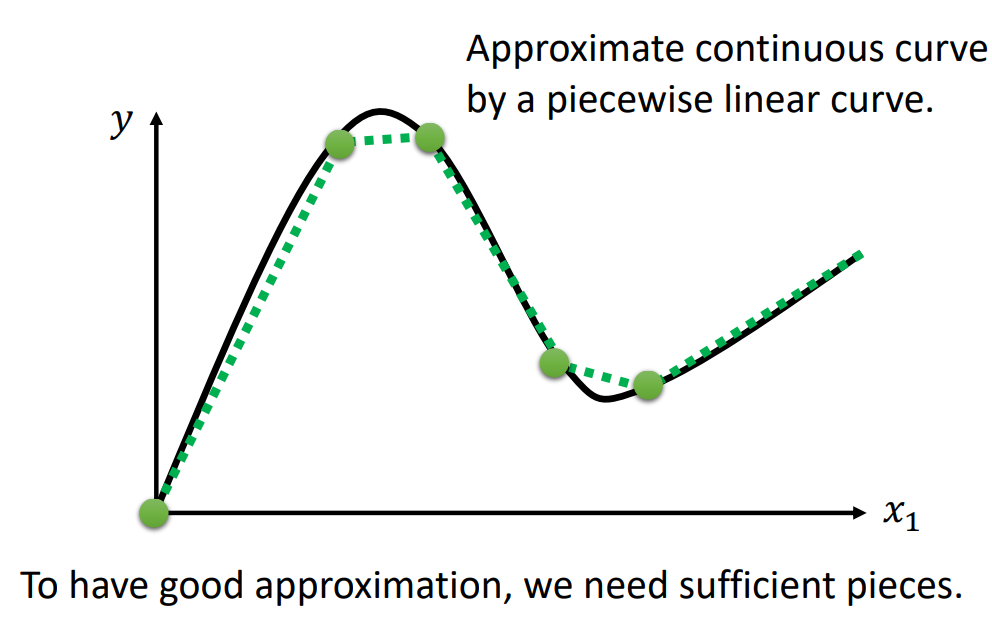
2.1.2 分段线性曲线(piecewise linear curve)
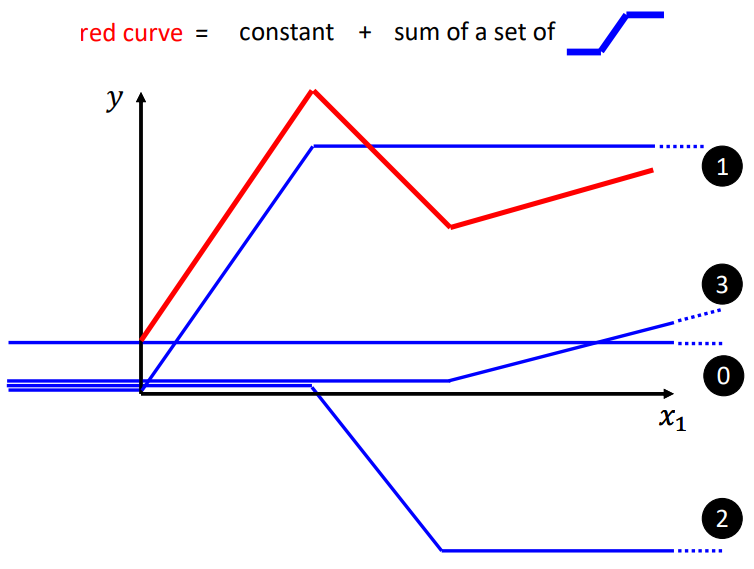
红线是分段线性曲线,它可以由多条蓝色线构成。而蓝线可以由sigmoid函数逼*,因此它也有一个常见的名字:Hard sigmoid.很显然我们需要不同的hard function,因此需要调整w和b、c的值.下图中的 0 + 1 + 2 + 3 加在一起就变成了红线,所以用一堆的 hard sigmoid函数加上一个常数可以组成分段线性曲线.
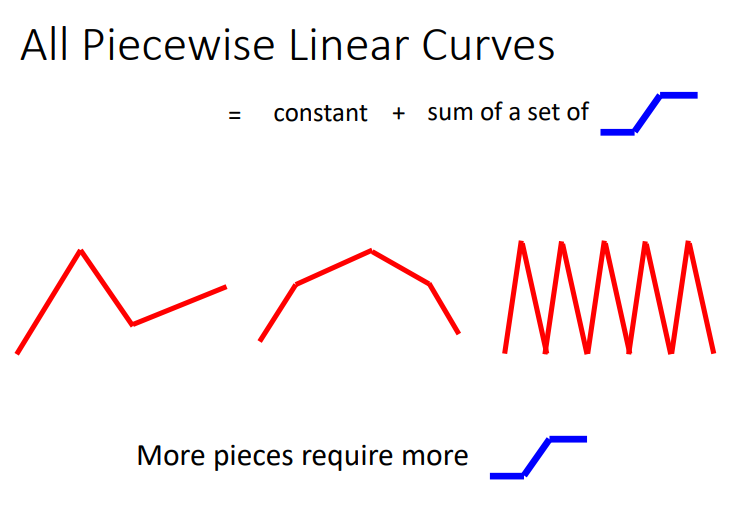
分段线性曲线的折线越多,需要的 hard sigmoid函数就更多,从左到右,需要的 hard sigmoid 在增多!
2.1.3 Hard Sigmoid
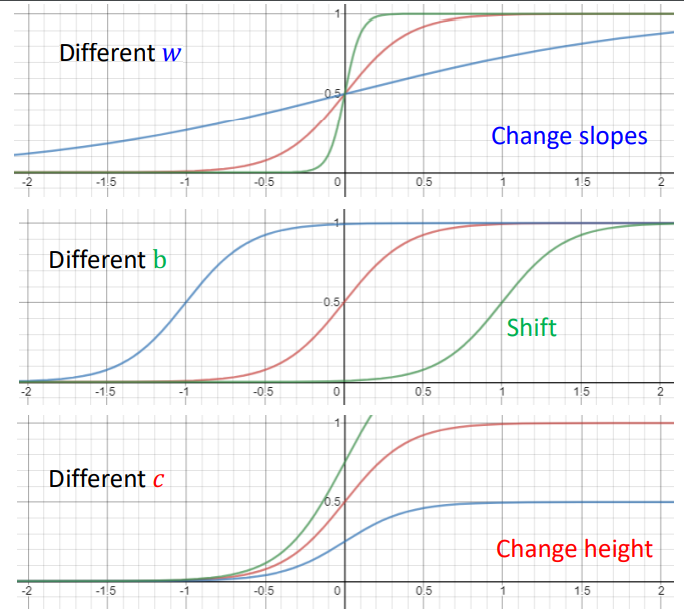
hard sigmoid 可以组成分段线性曲线,而 hard sigmoid 可以用 sigmoid(S型曲线)来代表,因为差别很小可以忽略。S型曲线中的 c、b、w都是参数,需要机器学出来。
为什么不将 hard sigmoid 作为基础函数呢?因为转角处无法求微分,所以要用一个*滑的曲线做基础函数。

改变w、c、b得到的曲线变化情况不同.
2.2 如何表示更复杂的模型:多自变量时
为了减小model bias,我们在寻找更有弹性的模型。前面讲的不用线性曲线,改用分段线性曲线表示,是针对一个feature(自变量)而言;而接下来讲的不用线性曲线,改用分段线性曲线表示,是针对多个feature(自变量)而言.

i表示有i个sigmoid曲线,j表示有j个 feature.总体思想就是分段函数可以分段看,每一段是线性的,每一段由一个sigmoid函数表示,最后将sigmoid函数组合在一起就变成了分段函数。有几个sigmoid就只能产生几段线.sigmoid的括号里面就是sigmoid能表示的线段.
图解上面蓝框框式子.sigmoid的括号里的东西可以用r表示\(r_1\)就是第 1 个\(sigmoid\)表示的线段,\(r_2\)就是第2个sigmoid表示的线段。\(w_{ij}\):在第i个sigmoid中乘给第j个自变量的权重
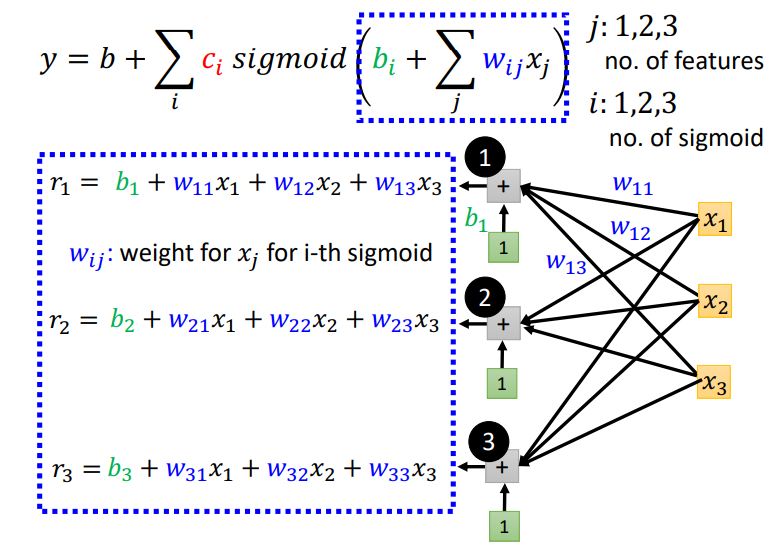
\(r\)可以用矩阵表示,在线性代数中常见.
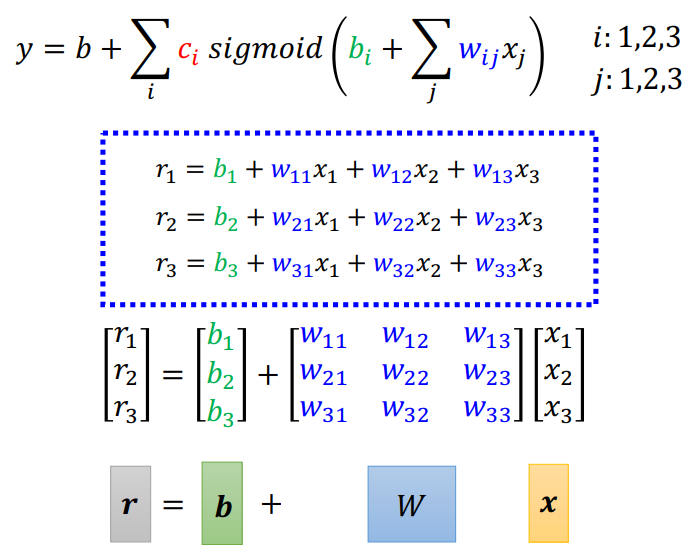
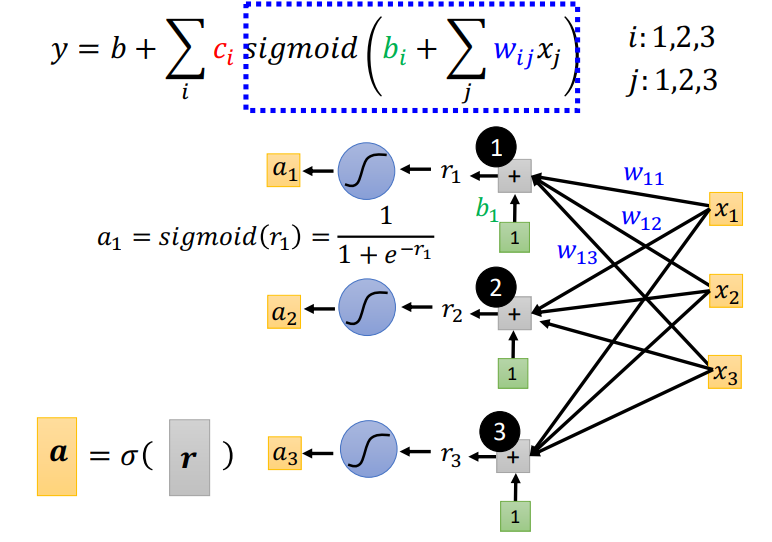
上面讲解了蓝色方框的构成.接着将\(r\)进行\(sigmoid\)操作形成 \(a\),每一个\(a\)对应一个\(sigmoid\)的输出.
然后将每一个\(sigmoid\)的输出\(a\)叠加在一起,再加上一个常数 \(b\),这样就组成了分段线性曲线!!

所以解构分段线性曲线的过程就是下图这样,线性代数的表示在最下一排.针对多个自变量的线段,经过\(sigmoid\)可以用来表示分段线性曲线中的一段,那么多个\(sigmoid\)就可以组成一个完整的分段线性曲线了.
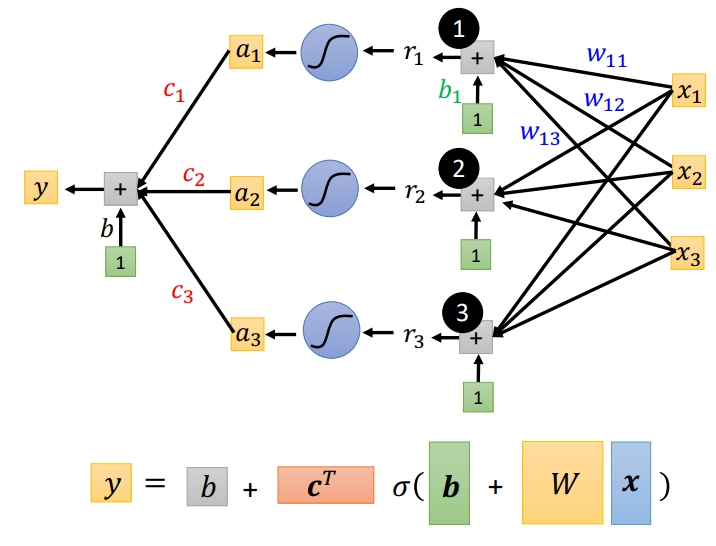
自变量只有x,其他全部都是机器要学习的参数,将这些表示参数的矩阵拉直组合在一起,就抽象成了一组未知参数!(注意:绿色b是向量,而灰色b是数值)
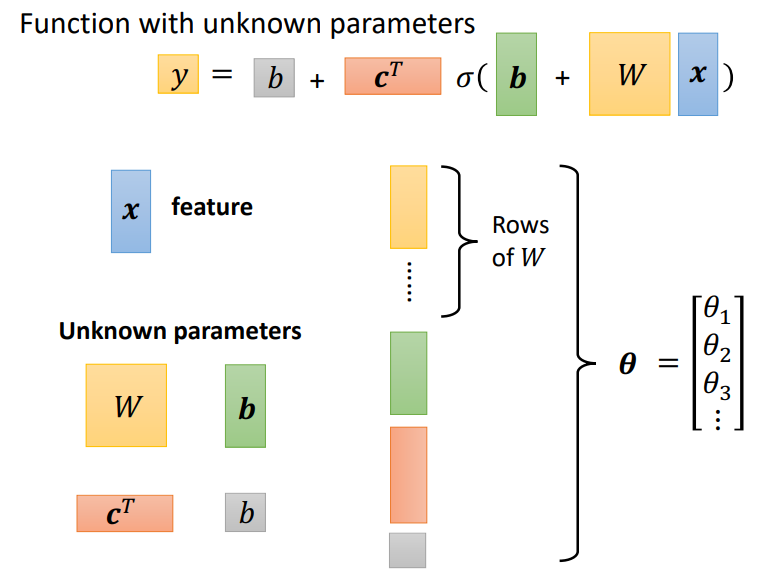
2.3 回到优化:对优化过程进行抽象泛化
所有的未知参数都抽象成\(\theta\),并将所有\(\theta\)放在一起组成一个向量,优化过程就是寻找能使 Loss 最小的\(\theta\)向量。将所有的偏微分放在一起组成一个向量g(梯度),所以更新参数就变成了更新向量了。

泛化后的优化过程如下所示(也就是找参数的过程):
1、定初值参数向量.
2、计算在该点处的梯度,并更新到新的参数位置.
3、迭代更新直至梯度g为0,但是g到0非常难,实际操作中不会算到g为 0,都是自己决定什么时候停下来不更新了.

2.3.1 优化的实际操作
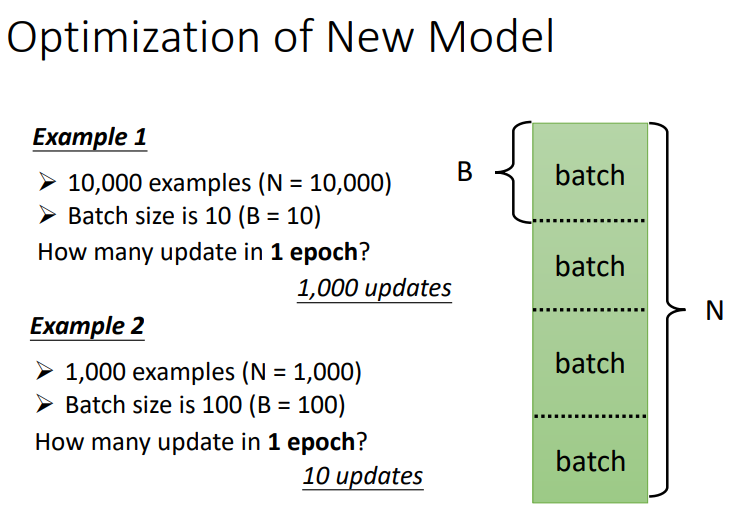
与优化的理论操作不一样的地方是:实际操作不会去算整个资料的\(loss\)然后才求梯度,而是将资料分成很多批,每次更新都只用一批(\(batch\))资料来算梯度!下次更新的时候又换一批资料算梯度.当看完了整个资料,也就是所有\(batch\)都使用到时,就叫一个\(epoch\).

我们可以回忆下深度学习训练过程,都是在一次batch训练后更新参数,因此当N=10000,Batch_size=10时,需要经过了1000次参数更新.
2.4 回到猜测函数:如何表示更复杂的模型
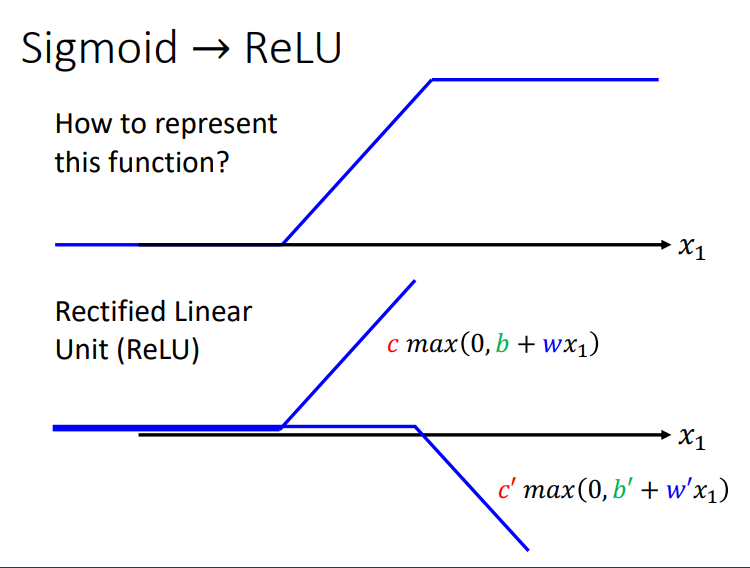
hard sigmoid 不仅可以用\(sigmoid\)来代表,它也可以用\(ReLU\)来代表.仔细看看下图是怎么通过ReLU来表示的,也就是由两段RELU合成,前面两段的合成好理解,最后这一段水*线的合成这样理解:\(ReLU\)中的两条斜线分别为 y = kx + b,y = -kx + b′,两斜线相加得到的 y 就是 b + b′(是一个定值),就能表示最后这一段水*线了.
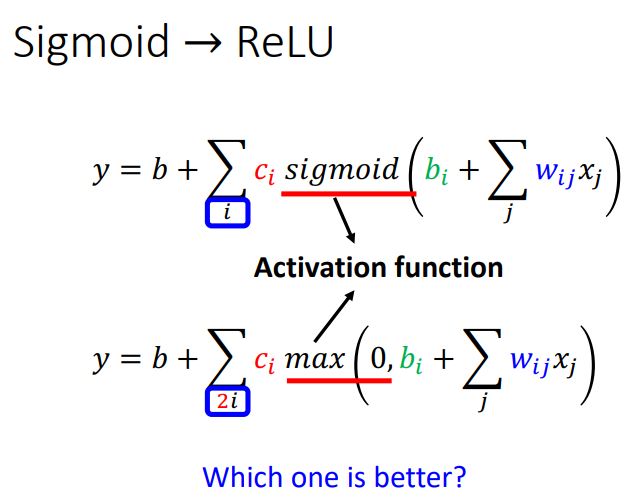
sigmoid 和 ReLU 两者都叫做 activation function(激活函数),两者不同之处在于 sigmoid 是用一个函数逼*一个 hard sigmoid,而 ReLU 则是用两个函数逼*一个 hard sigmoid。ReLU的效果更好,所以 ReLU 是更常用的.
2.5 图解如何表示更复杂的模型
下面两张图中,第一幅是图解单层神经网络,第二幅是图解多层神经网络!!多层神经网络就是先不把激活函数的输出a加在一起,而是再经过多层激活函数之后输出\(a^′\),将\(a^′\)加在一起作为输出.
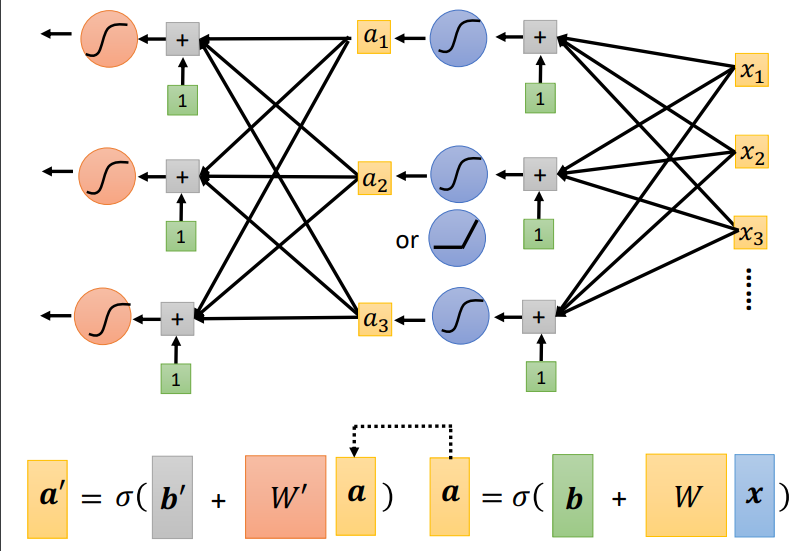
每个激活函数(例如sigmoid、ReLU)都是一个neuron(神经元),每一隐藏层中包含多个神经元.所有的这些东西便组成了neural network(神经网络).
在实际应用中,需要复杂的函数来做任务,一般复杂的函数有连续曲线,分段函数.我们构建的神经网络就是想通过简单的函数来模拟这些复杂的函数,通过激活函数便能用简单线段逼*复杂曲线.
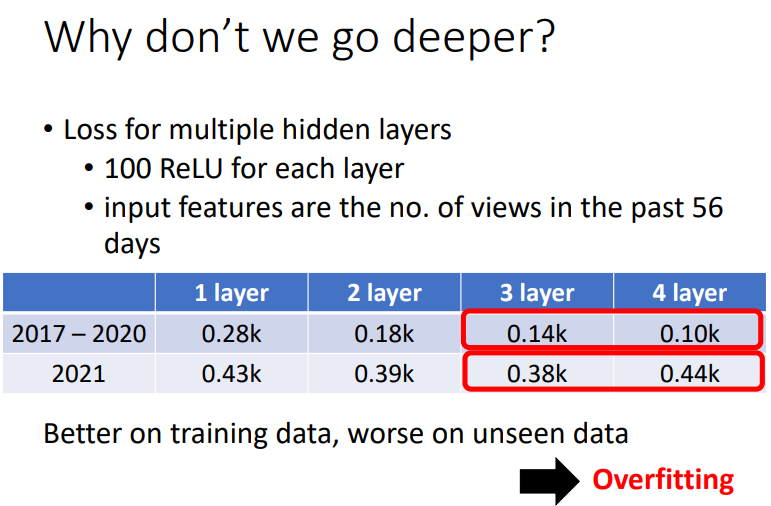
但是隐藏层也不能太多,网络一旦太深,就容易产生 overfitting(过拟合):在训练资料上有很好的表现,但是在测试资料上却表现很差,也就是在实际预测中没卵用!
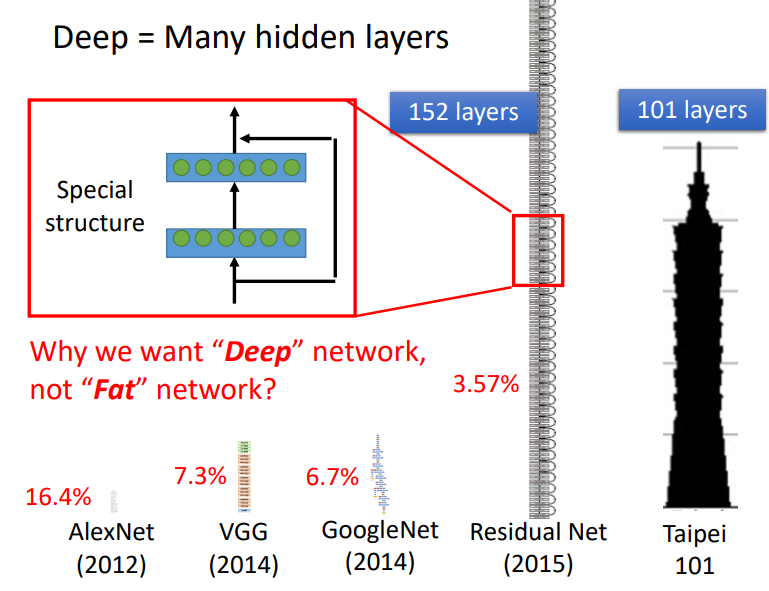
这里注意一下:胖是指网络有更多的特征,而深是指网络有更多的层数.
3. Google Colab
免费使用GPU来训练模型.允许使用Linux和python语法,但是使用Linux时,需要先使用一个!.
3.1 如何通过Google drive下载
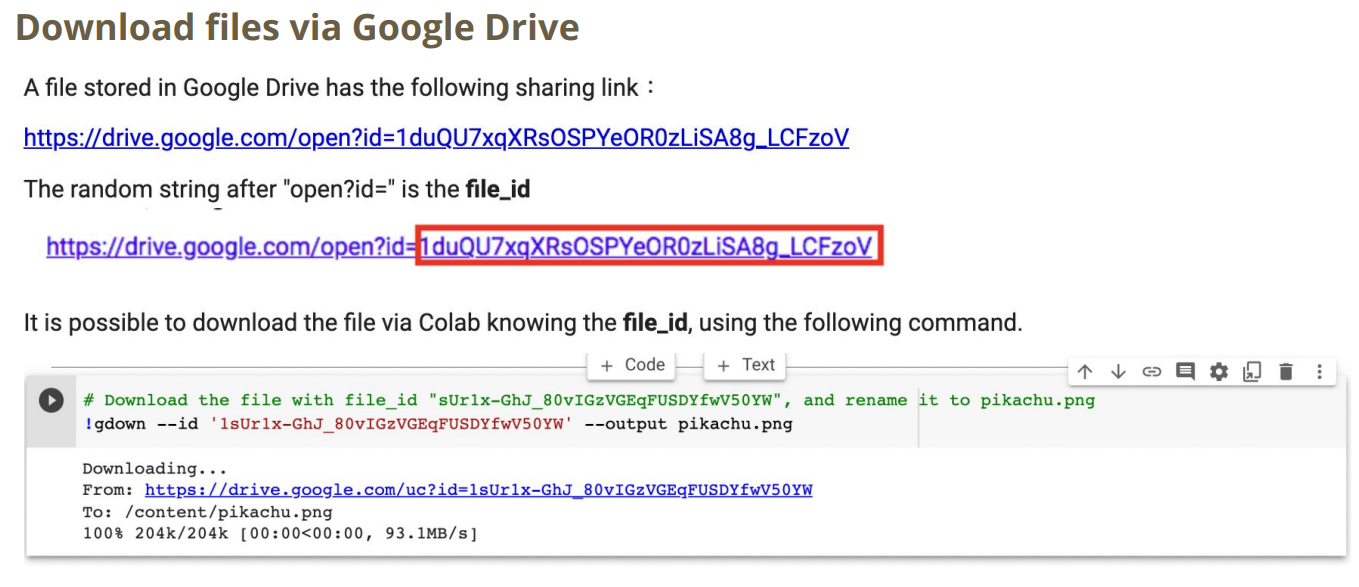
3.2 Colab常用指令

4. Pytorch
4.1 DataSet & DataSetloader
用于处理数据集和批处理数据集.

4.2 Tensor
要处理的数据必须由Pytorch转为Tensor.
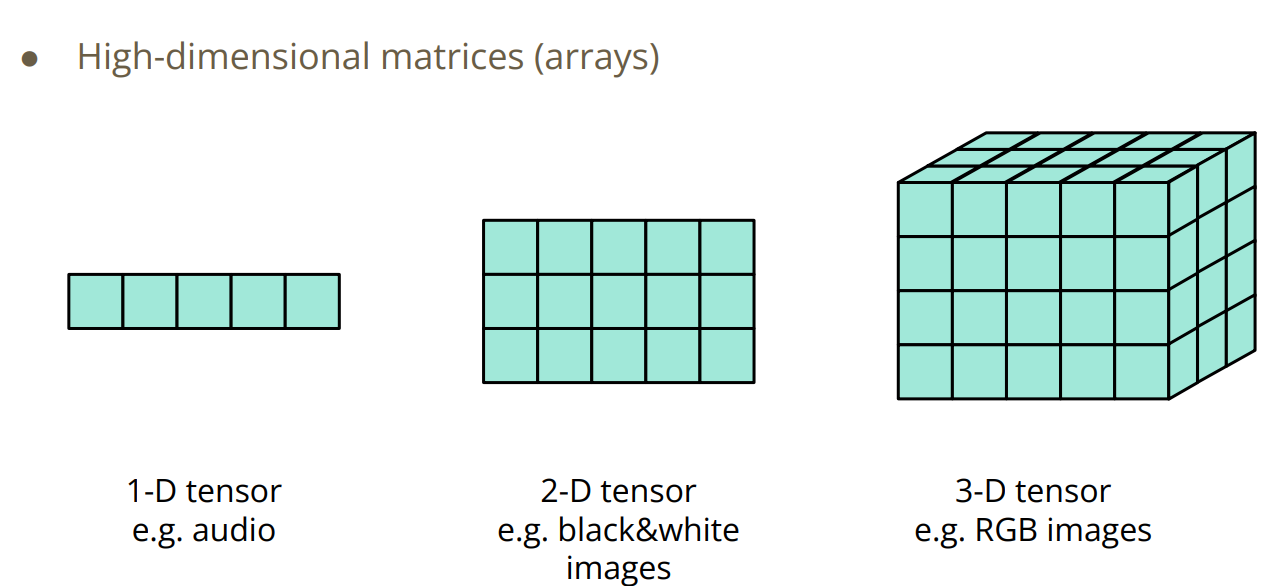
4.2.1 Tensor 基本操作
主要是加减乘除以及转置.


还有一个很重要的操作是降维:

以及升维:

常用的操作还包括concat:

4.2.2 Tensor CUDA
我们经常需要让模型在GPU上运算,这样更快.

4.2.3 Tensor 计算梯度

4.3.4 Pytorch Loss
用于衡量误差.

4.3.5 选择优化算法
大多使用Adam.


4.3.6 训练模型套路
建议不看这个,直接\(Google\)深度学习模型训练模板




我们计算梯度是为了调整模型,当计算测试集和验证集时,梯度计算是不必要的.

4.3.7 模型保存和读取
十分重要的步骤,将模型投入其他应用的操作.

同时解释一下,当官方文档的函数输入存在*,它表明在它后面的参数要在传递参数一定要指明参数名.

5. HW01
作业做到Colab不允许连GPU了,只试到了Strong BaseLine.
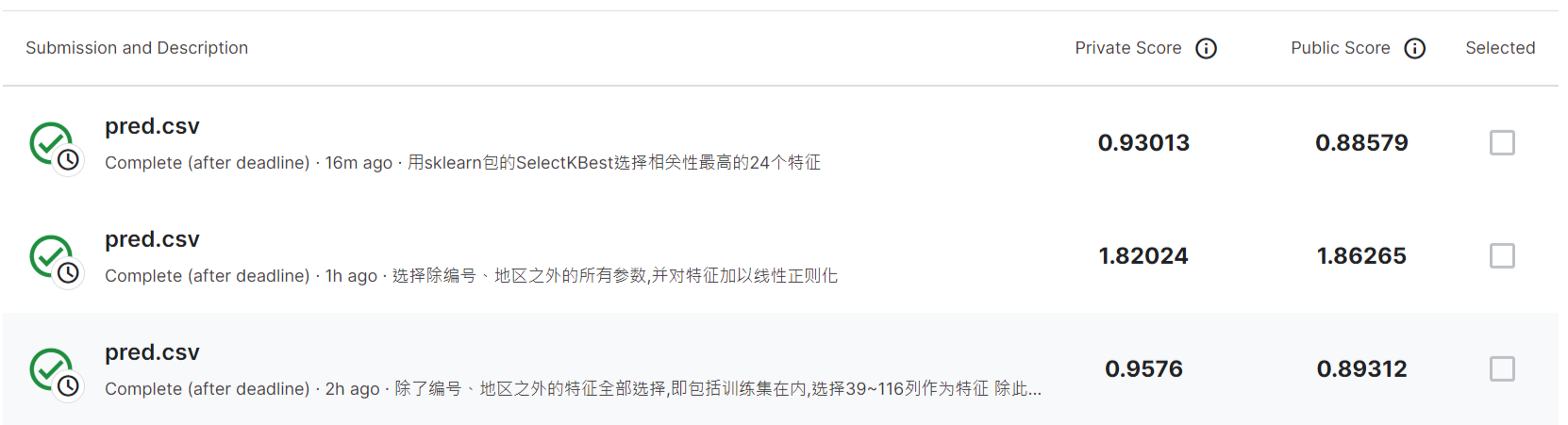
尝试过网上的Boss Baseline方法,结果还没收敛就早停了,可能早停法要设大一点.
6. 深度学习简介(选修)
深度学习的步骤与机器学习类似,参考了把大象放进冰箱的三个步骤.
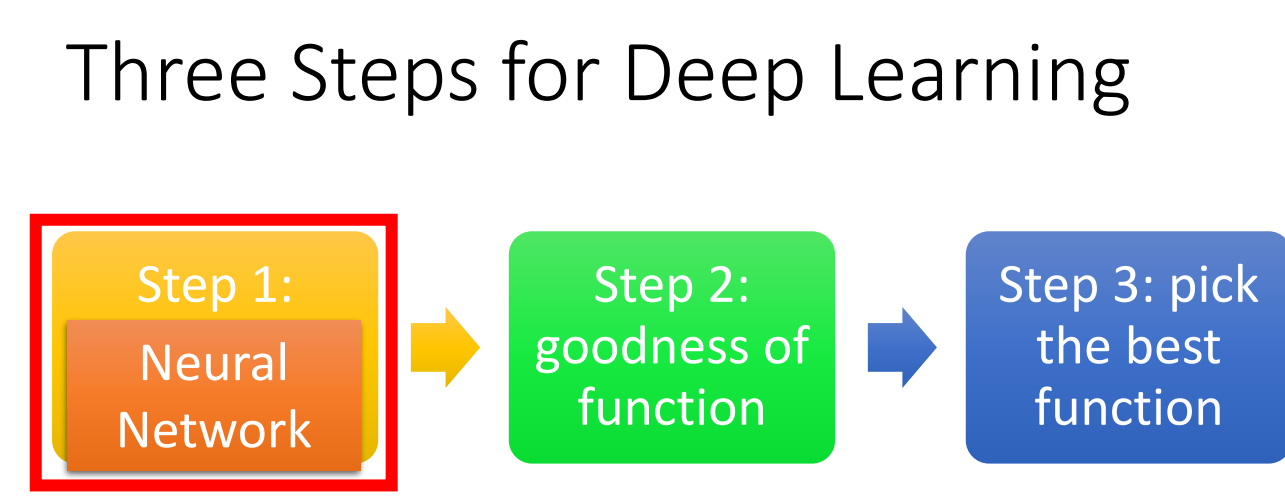
第一步定义网络,实际是定义一堆函数.每个函数的输出作为下一个函数的输入.
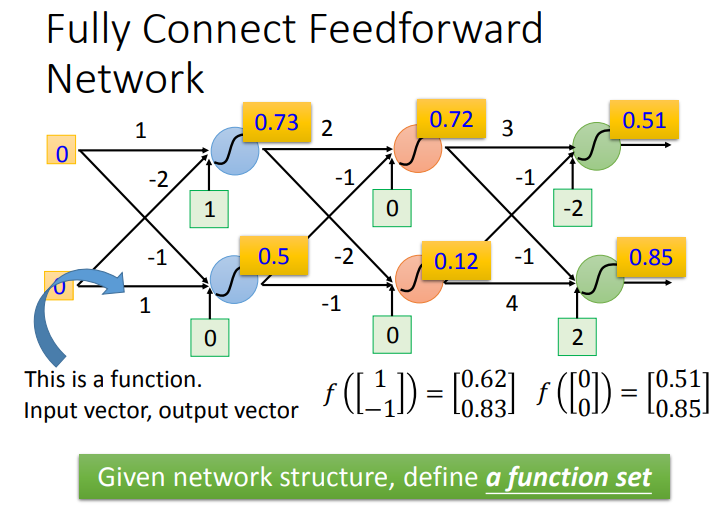
网络中的每层神经元与相邻层是两两相互连接的.这种网络也叫Fully Connect Feedforward Network.
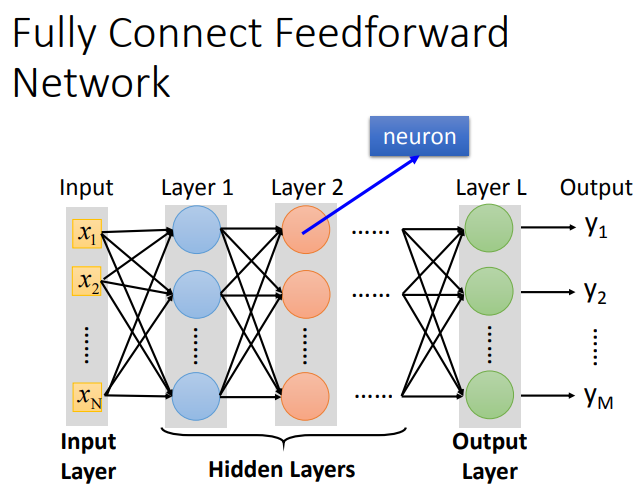
全连接网络分为输入层、隐藏层、以及输出层.当隐藏层数量很多时,这就是Deep的含义.同时,隐藏层可以看作特征提取.
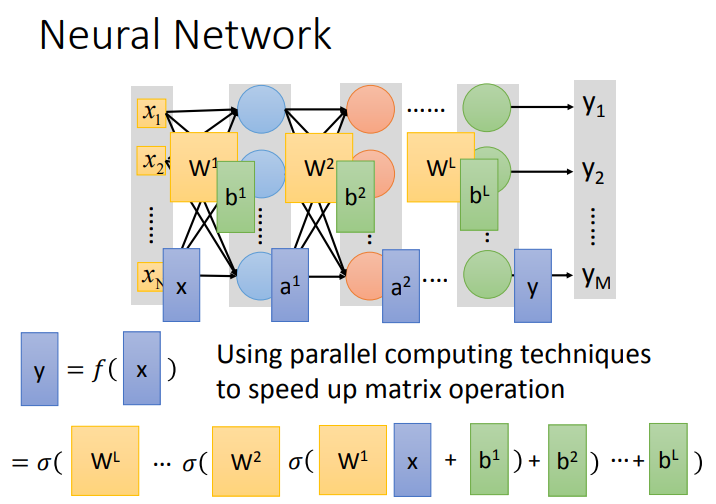
全连接层的计算可以转化为矩阵.不断地计算直到输出output.

二三步是衡量误差以及下降误差.下面举例是梯度下降.

7. 反向传播选修
下图是梯度下降的步骤.在神经网络中存在非常多的参数,为了有效地计算每个梯度的参数,提出了反向传播算法.

反向传播中使用的方法是链式法则.

那么链式法则是怎么在网络中应用的呢?可以知道网络输入一个\(x\),经过计算得到\(y\),它与实际标签\(y^n\)存在一个空间上的距离\(C^n\).将每个参数的\(C^n\)相加即是\(L(\theta)\).w对Loss求微分,可以转换为下面的公式.

我们可以使用链式法则将算式分解.
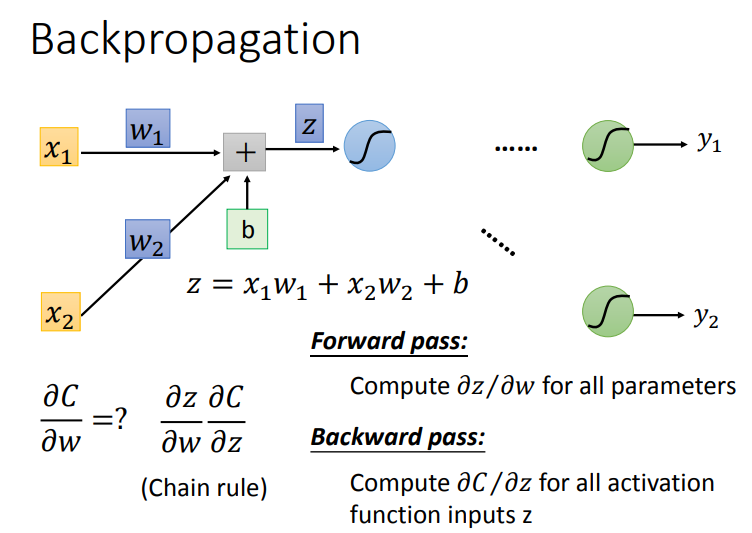
分步讲解一下.Forward Pass根据下面图求解很简单.我们也可以在其中发现规律,也就是微分的结果是当前权重的输入.
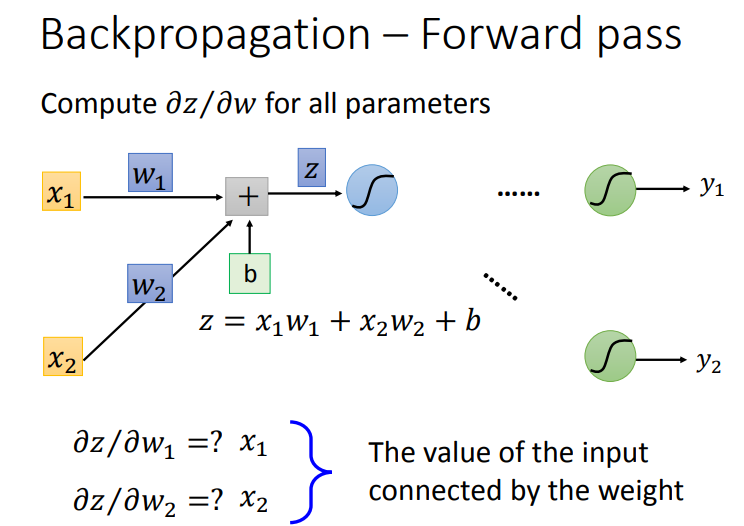
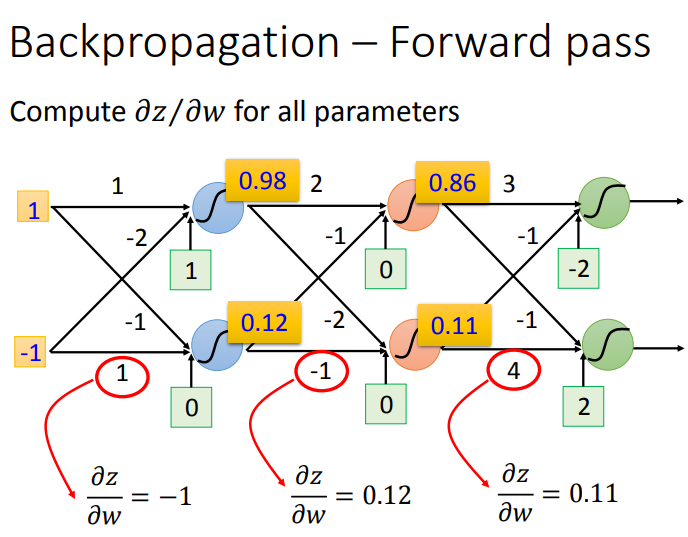
这样就可以很快求出神经网络的每个Forward Pass的值.
在算式的Backward Pass,也是使用链式法则计算.

我们可以发现计算Backward Pass不断地需要后面的微分,但如果我们先计算后面的微分,就不必递归计算,这也是反向传播提出的原因.


