机器学习 吴恩达 第十六章 笔记
十六、大规模机器学习(Large Scale Machine Learning)
16.1 大型数据集的学习
如果我们有一个低偏差的模型,增加数据集的规模可以帮助你获得更好的结果.但是,大部分大数据集学习都有一个计算问题.
以线性回归模型为例,假如我们有一亿样本,每一次梯度下降迭代,我们都需要计算训练集的误差的平方和,如果我们的学习算法需要有20次迭代,这便已经是非常大的计算代价.

此时,首先应该做的事是去检查一个这么大规模的训练集是否真的必要,也许我们只用1000个训练集也能获得较好的效果,我们可以绘制学习曲线来帮助判断.左图是高方差算法的典例,此时增大训练集是有效果的,而右图是高偏差算法,此时增大规模是没意义的.
16.2 随机梯度下降法
我们使用梯度下降算法来优化参数,但普通的梯度下降对大数据集来说计算量太大了,我们可以尝试使用随机梯度下降法来代替批量梯度下降法.
随机梯度算法适用于前面我们介绍的线性回归、神经网络等基于梯度下降的算法.
我们可以稍微复习一下批量梯度下降(叫批量是因为每次我们都要考虑全部样本):

上面的问题是,当\(m\)很大的时候,梯度下降的\(\sum\)就会需要很大的计算量.在随机梯度下降法中,我们定义代价函数为一个单一训练实例的代价:
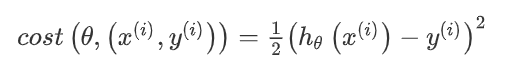
随机梯度下降算法为:首先对训练集随机"洗牌"(打乱样本顺序),然后:

其中,\((h_{\theta}(x^{(i)})-y^{(i)})\times x_j^{(i)}\)是\(cost\)函数对\(\theta_j\)的偏导数.
随机梯度下降算法在每一次计算之后便更新参数\(\theta\),而不需要首先将所有的训练集求和,在梯度下降算法还没有完成一次迭代时,随机梯度下降算法便已经走出了很远.也就是说,随机梯度下降每次都是只考虑拟合当前样本\(x^{(i)}\),而批量梯度下降每次移动是考虑所有样本\(\sum x^{(i)}\).注意循环,随机梯度下降是用一组数据修改全部\(\theta\),而批量梯度下降是每个\(\theta\)修改都用全部数据.
但是这样的算法存在的问题是,不是每一步都是朝着"正确"的方向迈出的.因此算法虽然会逐渐走向全局最小值的位置,但是可能无法站到那个最小值的那一点,而是在最小值点附近徘徊.
最后,随机梯度下降的最外层循环次数取决于数据集规格,一般1次就足够了,最多10次.
Click,看视频会觉得计算量不是一模一样吗?链接的知乎给了解释.
16.3 Mini-Batch梯度下降
小批量梯度下降算法是介于批量梯度下降算法和随机梯度下降算法之间的算法.批量梯度下降每次下降使用全部样本,而随机使用一个样本,那么Mini-Batch每次使用\(b\)个样本.

通常我们会令b在 2-100 之间.

比随机梯度靠谱一点是因为取b个样本更能保证更新是沿着代价函数减少的方向.这样做的好处在于,我们可以用向量化的方式来循环b个训练实例,如果我们用的线性代数函数库比较好,能够支持平行处理(多个样本能够发挥向量化的优势),那么算法的总体表现将不受影响(与随机梯度下降相同).
16.4 随机梯度下降收敛
本节我们探讨如何确定随机梯度下降已经收敛以及如何选择学习率\(\alpha\).
在批量梯度下降中,我们可以令代价函数\(J\)为迭代次数的函数,绘制图表,根据图表来判断梯度下降是否收敛.但是,在大规模的训练集的情况下,这是不现实的,因为计算代价太大了.
在随机梯度下降中,我们在每一次更新\(\theta\)之前都计算一次代价,然后每\(x\)次迭代后,求出这次对训练实例计算代价的平均值,然后绘制这些平均值与\(x\)次迭代的次数之间的函数图表.
注意右上角的图,我们得到了明显下降趋势的图,但如果我们把样本数增加(1000->5000),那么下降趋势会更加平滑(但是这样需要更多数据才能得到一个数据点),得到的算法反馈也越延迟.
当我们绘制这样的图表时,可能会得到一个颠簸不平但是不会明显减少的函数图像(如上面左下图中蓝线所示).我们可以增加样本数(1000->5000)来使得函数更加平缓,也许便能看出下降的趋势了(如上面左下图中红线所示).或者可能函数图表仍然是颠簸不平且不下降的(如洋红色线所示),那么我们的模型本身可能存在一些错误.
随机梯度算法不是直接收敛到全局最小值,而是在一个范围来回振荡,然后收敛到全局最小值的近似值.但是如果我们使用更小的学习率,振荡就会变小,得到更小的结果(但有时候差别不大).
我们观察右下角图,当曲线上升时,我们要考虑使用更小的学习率\(\alpha\)(下降的步长).
如果我们想要让随机梯度下降不是简单地收敛到最小值的近似值(如果\(\alpha\)不变一般就是这种情况),就可以令学习率随着迭代次数的增加而减小,例如令:
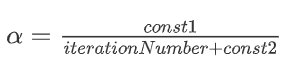
其中,iterationNumber是当前运行随机梯度算法的迭代次数(已经计算过的训练样本数量).随着迭代次数的增加,下降的步子会越来越小,收敛会越来越精准.这种方法需要花时间来尝试const1和const2,因此我们使用很少.
16.5 在线学习
本节讨论一种新的大规模的机器学习机制,叫做在线学习机制.在线学习机制让我们可以模型化问题,也就是我们有连续的数据流,想要用算法从中学习.
许多大型网站或者许多大型网络公司,使用不同版本的在线学习机制算法,从大批的涌入又离开网站的用户身上进行学习.特别要提及的是,如果你有一个由连续的用户流引发的连续的数据流,进入你的网站,你能做的是使用一个在线学习机制,从数据流中学习用户的偏好,然后使用这些信息来优化一些关于网站的决策.
假定你有一个提供运输服务的公司,用户们来向你询问把包裹从A地运到B地的服务,同时假定你有一个网站,让用户们可多次登陆,然后他们告诉你,他们想从哪里寄出包裹,以及包裹要寄到哪里去,也就是出发地与目的地,然后你的网站开出运输包裹的的服务价格.比如,我会收取$50来运输你的包裹,我会收取$20之类的,然后根据你开给用户的这个价格,用户有时会接受这个运输服务,那么这就是个正样本,有时他们会走掉,然后他们拒绝购买你的运输服务.所以,让我们假定我们想要一个学习算法来帮助我们,优化我们想给用户开出的价格.

在线学习算法的一个应用就是产品搜索功能.比如点击率预测学习问题.假设我们经营一家商店,我们贩卖多个手机,当用户点进商店,我们需要根据特征给用户推荐手机,预测用户点击推荐手机的概率.配合这10个样本,我们又可以使用Mini-Batch梯度下降来优化参数.

与之前的学习问题最大的区别是不再有固定的训练集样本,而是使用连续的数据流来学习,学完就丢.
16.6 减少映射与数据并行
映射化简和数据并行对于大规模机器学习问题而言是非常重要的概念.之前提到,如果我们用批量梯度下降算法来求解大规模数据集的最优解,我们需要对整个训练集进行循环,计算偏导数和代价,再求和,计算代价非常大.如果我们能够将我们的数据集分配给不多台计算机,让每一台计算机处理数据集的一个子集,然后我们将计所的结果汇总在求和,这样的方法叫做映射简化.
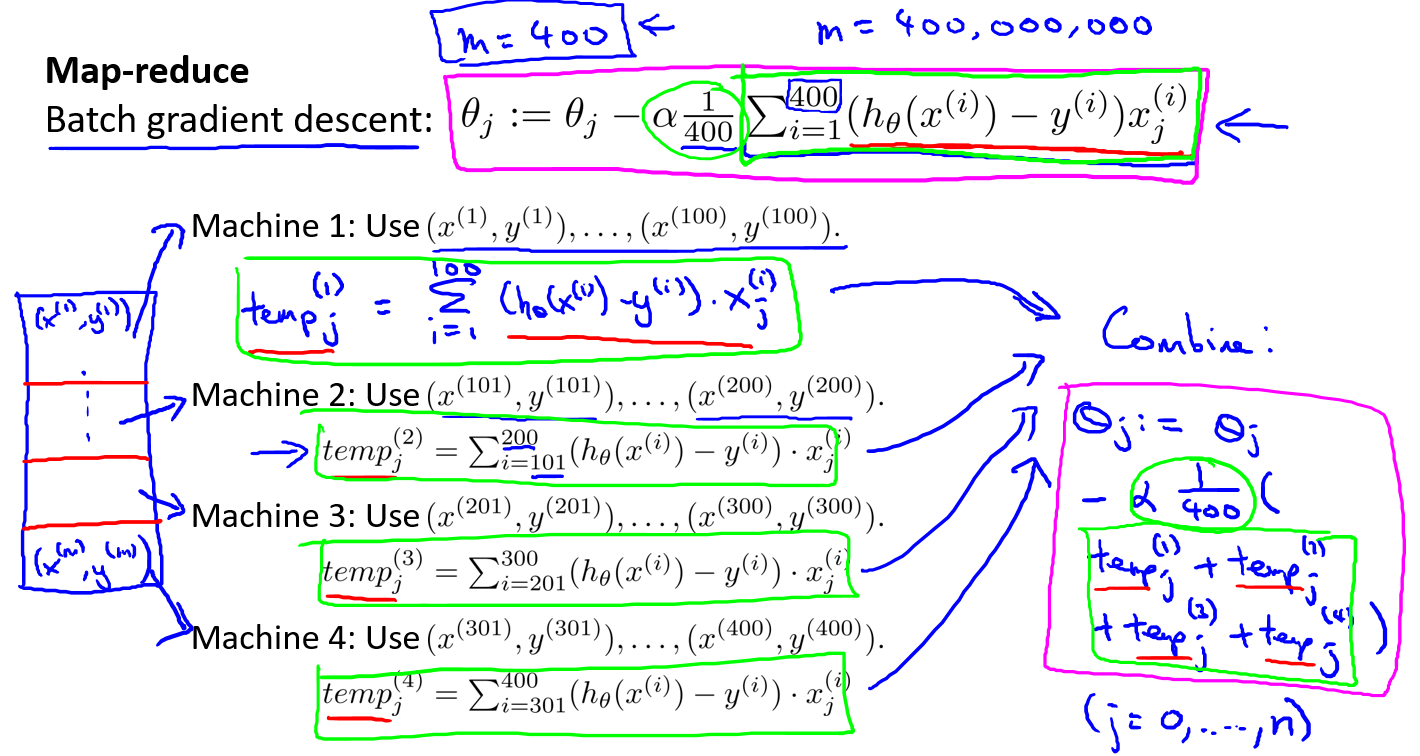
具体而言,如果任何学习算法能够表达为,对训练集的函数的求和,那么便能将这个任务分配给多台计算机(或者同一台计算机的不同CPU 核心),以达到加速处理的目的.

例如,我们有400个训练实例,我们可以将批量梯度下降的求和任务分配给4台计算机进行处理:

很多高级的线性代数函数库已经能够利用多核CPU的多个核心来并行地处理矩阵运算,这也是算法的向量化实现如此重要的缘故(比调用循环快).


