机器学习 吴恩达 第十二章 笔记

十二、聚类(Clustering)

12.1 无监督学习

  从本节开始,我们开始学习无监督学习,我们将要让计算机学习无标签数据,而不是此前的标签数据.
  那么,什么是非监督学习呢?在一个典型的监督学习中,我们有一个有标签的训练集,我们的目标是找到能够区分正样本和负样本的决策边界,在这里的监督学习中,我们有一系列标签，我们需要据此拟合一个假设函数.与此不同的是,在非监督学习中,我们的数据没有附带任何标签,我们拿到的数据就是这样的.

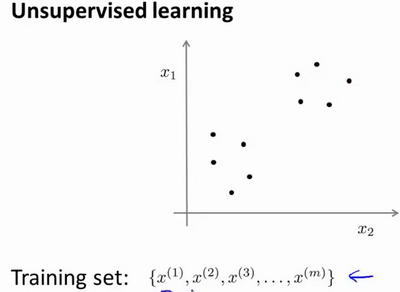
  在非监督学习中，我们需要将一系列无标签的训练数据，输入到一个算法中，然后我们告诉这个算法，快去为我们找找这个数据的内在结构给定数据。我们可能需要某种算法帮助我们寻找一种结构.图上的数据看起来可以分成两个分开的点集(称为簇),一个能够找到我圈出的这些点集的算法，就被称为聚类算法.
  当然还有其他非监督学习算法,它们可以为我们找到其他类型的结构或者其他的一些模式,而不只是簇.
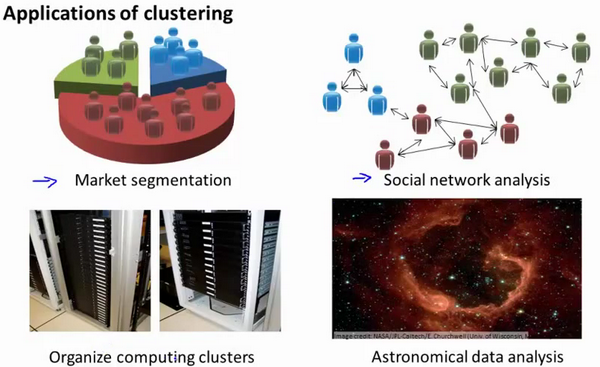
  那么,聚类算法有什么用呢?我们据一些例子,比如市场分割.也许你在数据库中存储了许多客户的信息，而你希望将他们分成不同的客户群,这样你可以对不同类型的客户分别销售产品或者分别提供更适合的服务.社交网络分析：事实上有许多研究人员正在研究这样一些内容，他们关注一群人,关注社交网络，例如Facebook，Google+，或者是其他的一些信息，比如说:你经常跟哪些人联系,而这些人又经常给哪些人发邮件,由此找到关系密切的人群

12.2 K-Means算法

  K-Means是最普及的聚类算法,算法接受一个未标记的数据集，然后将数据聚类成不同的组.
  K-Means是一个迭代算法,假设我们想要将数据聚类成n个组,其方法为:
(1) 首先选择$n$个随机的点,称为聚类中心(cluster centroids).
(2) k-Means方法会做两件事,第一件是簇分配:对于数据集中的每一个数据,按照距离$n$个中心点的距离,将其与距离最近的中心点关联起来,与同一个中心点关联的所有点聚成一类.
(3) 另一件是移动中心点.将该组所关联的所有点求均值,中心点移动到平均值的位置.
(4) 重复2-3直至中心点不再变化.

  正规写出K-Means算法,这个算法接收两个输入:K(簇类个数),X(训练集),顺便,X不需要假如一列$x_0=1$

Repeat {
 
	for i = 1 to m
	#求解离当前样本最近的簇类中心
		c(i) := index (form 1 to K) of cluster centroid closest to x(i)
		#一般距离用平方度量
	for k = 1 to K
		μk := average (mean) of points assigned to cluster k
}

  如果一个簇不存在点的话,一个简单的做法是直接移除那个簇类中心.但如果我们一定要$K$个簇的话,还有一种做法就再次随机化这个簇类中心.
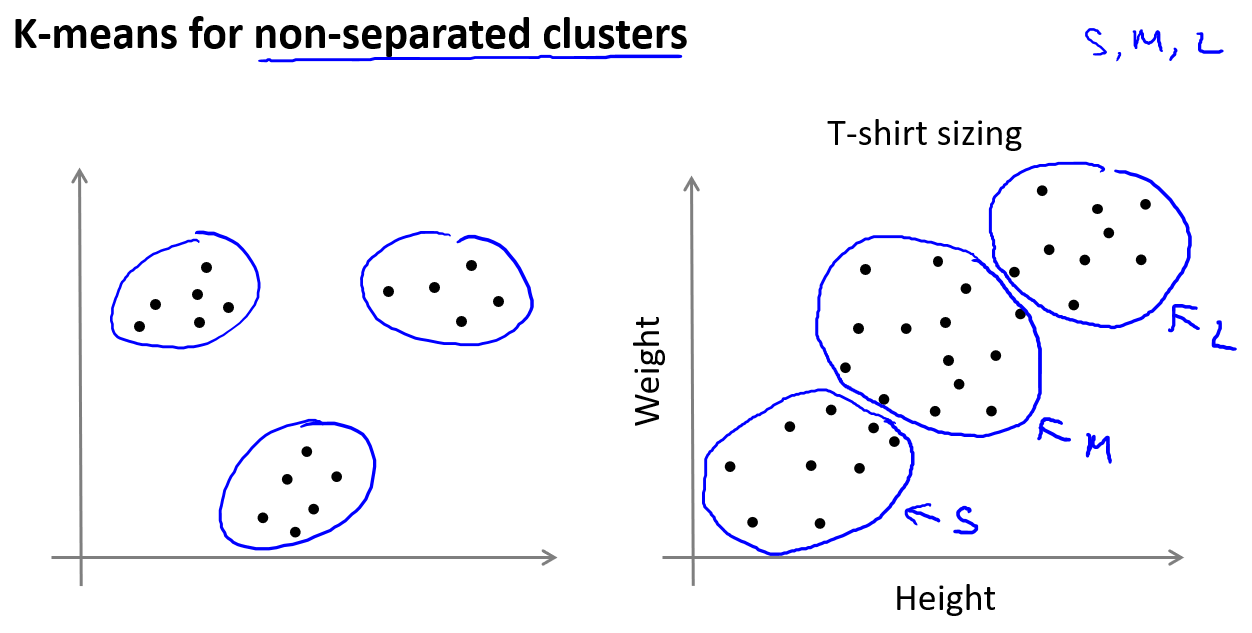
  举一个应用的例子:假设我们有一群人的不同身高体重的数据,我们需要将他们的数据分为三类,以便根据数据制作小号中号大号的衣服尺寸.

12.3 优化目标

  K-均值最小化问题,是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和,因此 K-均值的代价函数(又称畸变函数 Distortion function)为:

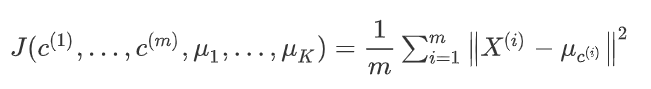
  也就是找到使得代价函数最小的$c^{(1)},c^{(2)},...,c^{(m)}$和$u_1,u_2,...,u_k$,最小化每个样本到其簇类中心点的距离的平方.
  代价函数的运用可以帮助$K-Means$算法避免局部最优解,还有一种好处是可以帮助调试算法.
  在K-means算法里,我们会对两个数值进行追踪,一个是$x^{(i)}$所属的集群$c^{(i)}$,第$k$个集群的均值位置($K$表示的是簇类数量,$k$表示的是簇的下标):

  回顾刚才给出的K-均值迭代算法,可以看出第一个循环是用于减小引起的代价,选出合适的$c^{(i)}$.而第二个循环就是在减小$u_i$引起的代价(均值使簇类中心往该类点密集处实现优化).迭代的过程一定会是每一次迭代都在减小代价函数,不然便是出现了错误.

12.4 随机初始化

  本节我们讨论如何初始化K均值聚类算法,涉及如何使用算法避开局部最优.
  在运行K-均值算法的之前,我们首先要随机初始化所有的聚类中心点,下面介绍怎样做:

1. 我们应该选择$K<m$,即聚类中心点的个数要小于所有训练集实例的数量
2. 随机选择K个训练实例,然后令K个聚类中心分别与这K个训练实例相等

  K-均值的一个问题在于随着初始化的情况不同,最后收敛的局势也可能不同,它有可能会停留在一个局部最小值处,而这取决于初始化的情况.

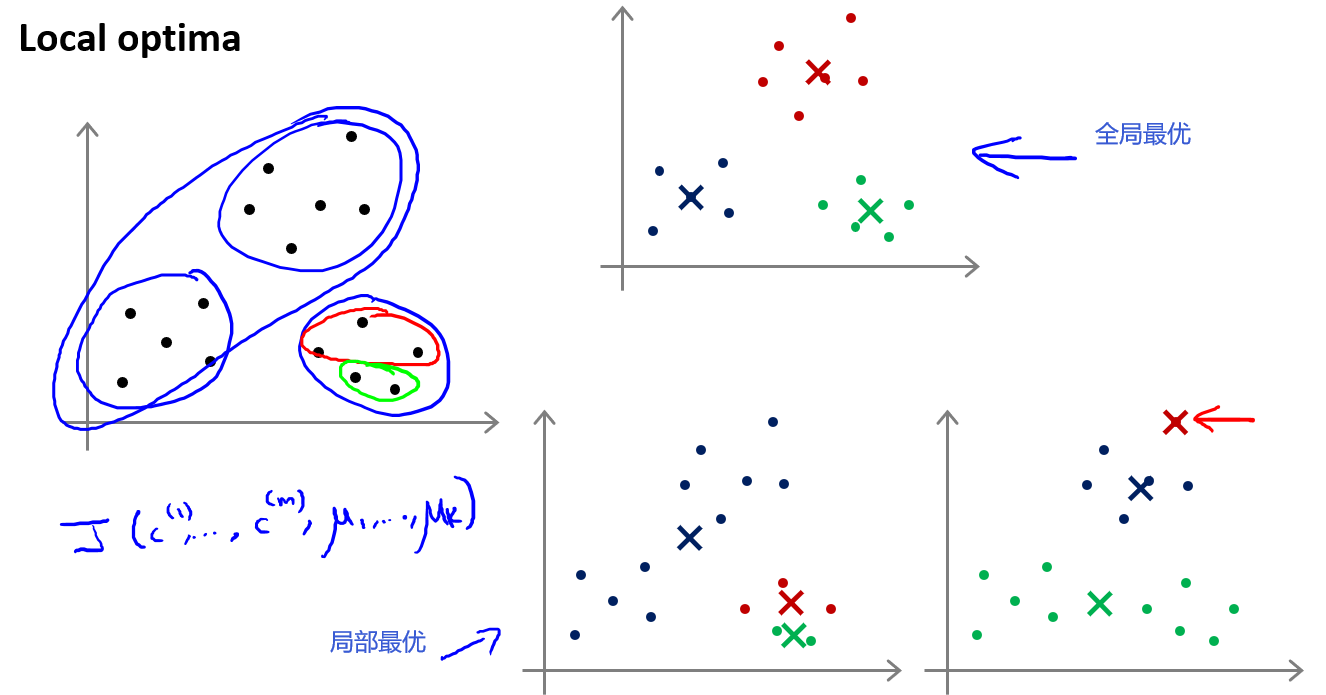
  为了解决这个问题,我们通常需要多次运行K-均值算法,每一次都重新进行随机初始化,最后再比较多次(50-1000)运行K-均值的结果,选择代价函数最小的结果.这种方法在K较小的时候(2--10)还是可行的,但是如果较大,这么做也可能不会有明显地改善.

12.5 选择聚类数

  本节讨论如何选择簇类数量(K).但没有所谓最好的选择聚类数的方法,通常是需要根据不同的问题,人工进行选择的.选择的时候思考我们运用K-均值算法聚类的动机是什么,然后选择能最好服务于该目的标聚类数.
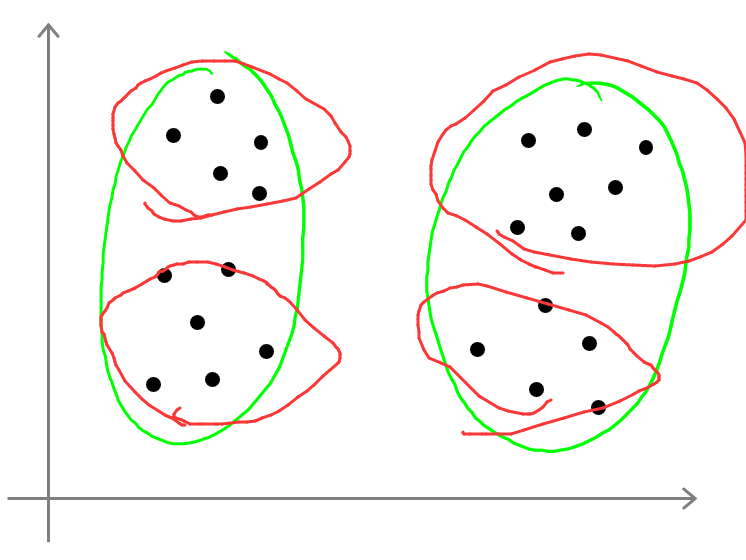
  从下面的图可以看出,簇类数量的选择即使从主观角度也很难选择,因此很难用自动化的方法求解K.

  当人们在讨论,选择聚类数目的方法时,有一个可能会谈及的方法叫作"肘部法则".这个法则我们所需要做的是改变$K$值,然后计算成本函数,最后绘图.

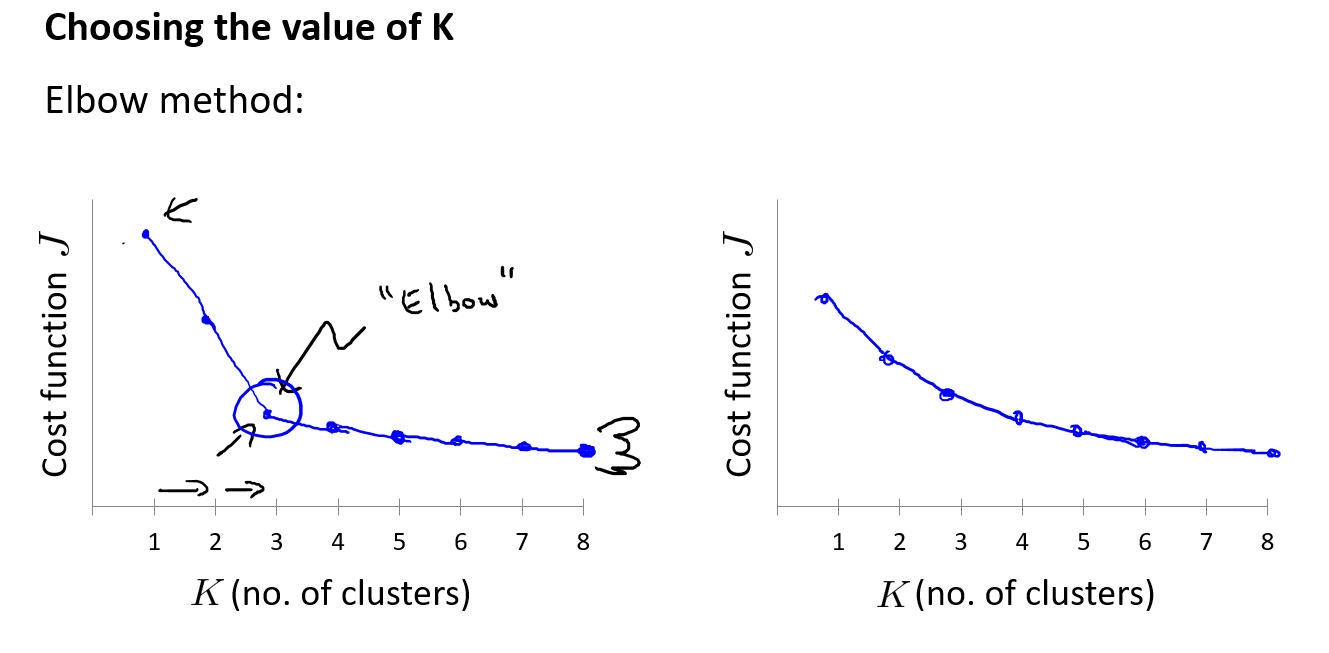
  我们可能会得到一条类似于这样的曲线.像一个人的肘部.这就是"肘部法则"所做的.我们可以发现一开始随着K增加,代价下降很快,当K=3时,下降速度放缓了很多,因此$K=3$是合适的选择.
  但也可能得到的曲线图拐点并不明显,比如上面右边的图.因此这个法则不能解决所有问题.
  还有一种方法选择$k$值是联系问题实际.例如,我们的 T-恤制造例子中,我们要将用户按照身材聚类,我们可以分成3个尺寸:S,M,L.也可以分成5个尺寸:XS,S,M,L,XL.样的选择是建立在回答"聚类后我们制造的T-恤是否能较好地适合我们的客户"这个问题的基础上作出的.