机器学习 吴恩达 第九章 笔记
九、应用机器学习的建议(Advice for Applying Machine Learning)
9.1 决定下一步做什么
确保你在设计机器学习的系统时，你能够明白怎样选择一条最合适、最正确的道路。因此，在这节视频和之后的几段视频中，我将向你介绍一些实用的建议和指导，帮助你明白怎样进行选择。具体来讲，我将重点关注的问题是假如你在开发一个机器学习系统，或者想试着改进一个机器学习系统的性能，你应如何决定接下来应该选择哪条道路？
为了解释这一个问题,我们仍然用预测房价的例子:假如你已经完成了正则化线性回归,也就是最小化代价函数\(J\)的值.你要将你的假设函数放到一组新的房屋样本上进行测试,假如说你发现在预测房价时产生了巨大的误差,现在你的问题是要想改进这个算法,接下来应该怎么办?际上你可以想出很多种方法来改进这个算法的性能:
1.比如给出更多训练样本.具体来讲,也许你能想到通过电话调查或上门调查来获取更多的不同的房屋出售数据.遗憾的是,我看到好多人花费了好多时间想收集更多的训练样本。他们总认为,要是我有两倍甚至十倍数量的训练数据,那就一定会解决问题的是吧?但有时候获得更多的训练数据实际上并没有作用.
2.另一个方法,你也许能想到的是尝试选用更少的特征集.你可以花一点时间从这些特征中仔细挑选一小部分来防止过拟合.
3.或者选取更多的特征.你希望从获取更多特征的角度来收集更多的数据.
4.增加多项式特征.
5.增大或减小正则化参数\(\lambda\).
现实中,大多数人都是凭感觉选择这些优化方法,但我们不应该随机选择上面的某种方法来改进我们的算法,而是运用一些机器学习诊断法来帮助我们知道上面哪些方法对我们的算法是有效的.
在接下来的两节中,我首先介绍怎样评估机器学习算法的性能，然后在之后的几节中,我将开始讨论这些方法,它们也被称为"机器学习诊断法"。“诊断法”的意思是:这是一种测试法,你通过执行这种测试，能够深入了解某种算法到底是否有用.这通常也能够告诉你，要想改进一种算法的效果，什么样的尝试,才是有意义的.
9.2 评估假设
在本节中我想介绍一下怎样用你学过的算法来评估假设函数.在之后的课程中,我们将以此为基础来讨论如何避免过拟合和欠拟合的问题.
当我们确定学习算法的参数的时候，我们考虑的是选择参量来使训练误差最小化,有人认为得到一个非常小的训练误差一定是一件好事，但我们已经知道,仅仅是因为这个假设具有很小的训练误差，并不能说明它就一定是一个好的假设函数(过拟合).
那么,你该如何判断一个假设函数是过拟合的呢?对于这个简单的例子,我们可以对假设函数\(h_{\theta}(x)\)进行画图,然后观察图形趋势,但对于特征变量不止一个的这种一般情况,还有像有很多特征变量的问题.但对于特征变量不止一个的这种一般情况,还有像有很多特征变量的问题,想要通过画出假设函数来进行观察,就会变得很难甚至是不可能实现.
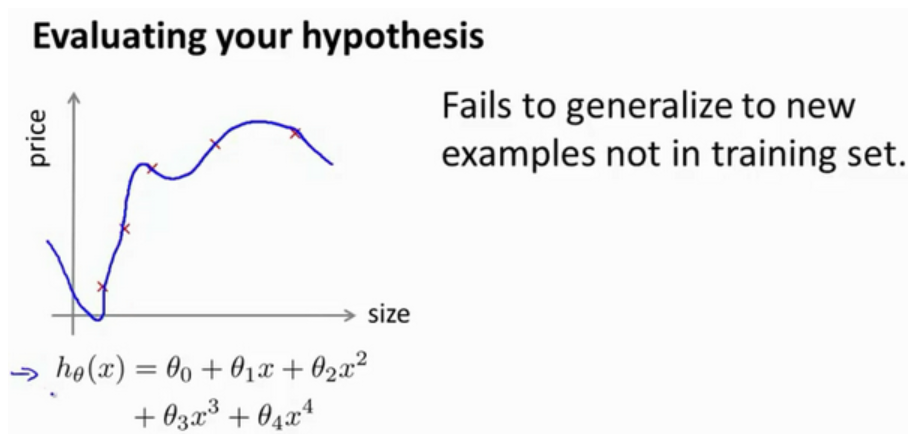
下面是一种评价算法的方法:
为了检验算法是否过拟合,我们将数据分成训练集和测试集,通常用70%的数据作为训练集,用剩下30%的数据作为测试集(最好是随机选择).很重要的一点是训练集和测试集均要含有各种类型的数据,通常我们要对数据进行"洗牌",然后再分成训练集和测试集.
一般而言,我们用下标\(test\)表示测试集.\(m_{test}\)表示测试集总数,而\((x_{test}^{(1)},y_{test}^{(1)})\)表示测试样本的第一组数据.
结合上面我们评价算法的一种方法是:
(1) 根据训练集学习算法得到参数\(\theta\)
(2) 用训练集的参数\(\theta\)计算测试集的误差.
测试集评估在通过训练集让我们的模型学习得出其参数后，对测试集运用该模型，我们有两种方式计算误差:
- 对于线性回归模型,我们利用测试集数据计算代价函数\(J\).
- 对于逻辑回归模型,我们除了可以利用测试数据集来计算代价函数外.
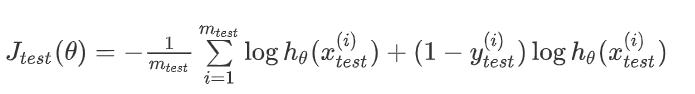
也可以使用错误分类,对于每一个测试集样本,计算:
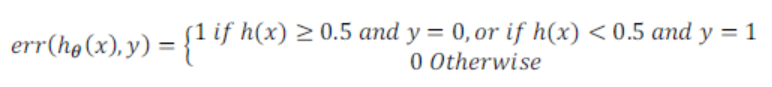
然后对计算结果求平均.
9.3 模型选择和训练、验证、测试集
如果想要确定一个数据集最适合的多项式次数,或者如何选择特征、正则化参数\(\lambda\).这类问题是模型选择问题.
接下来,我们要把数据集分为三部分:训练集、验证集、测试集.我们会讨论这个问题.
假设我们要选出最好拟合数据的多项式次数:
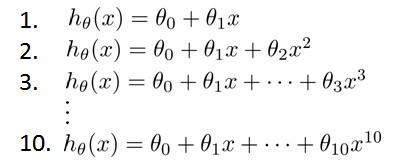
显然越高次数的多项式模型越能够适应我们的训练数据集,但是适应训练数据集并不代表着能推广至一般情况,我们应该选择一个更能适应一般情况的模型.一种做法是用交叉验证集来帮助选择模型. 即:使用60%的数据作为训练集,使用20%的数据作为交叉验证集(其中,交叉验证简称cv),使用20%的数据作为测试集.
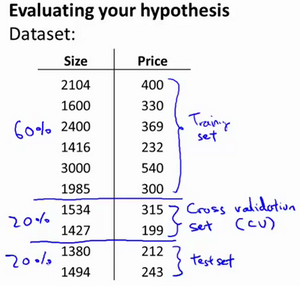
模型选择的方法为:
- 使用训练集训练出10个模型,最小化代价函数的值得到\(\theta\)
- 用10个模型分别对交叉验证集计算得出交叉验证误差(代价函数的值)
- 选取代价函数值最小的模型,这代表用交叉验证集选择最高项次数.
- 用步骤3中选出的模型对测试集计算得出推广误差(代价函数的值),以此计算泛化误差.
9.4 诊断偏差和方差
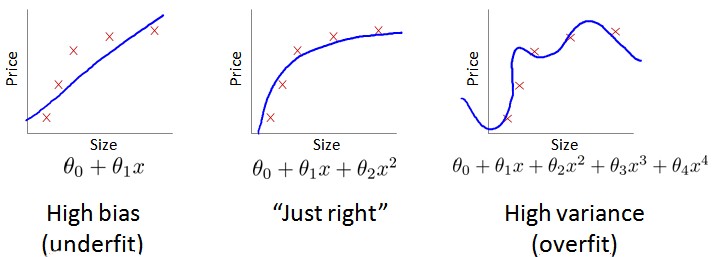
当你运行一个学习算法时,如果这个算法的表现不理想,那么多半是出现两种情况:要么是偏差比较大,要么是方差比较大.换句话说,出现的情况要么是欠拟合,要么是过拟合问题.那么这两种情况,哪个和偏差有关,哪个和方差有关,或者是不是和两个都有关?搞清楚这一点非常重要,因为能判断出现的情况是这两种情况中的哪一种.其实是一个很有效的指示器,指引着可以改进算法的最有效的方法和途径.在这段视频中,我想更深入地探讨一下有关偏差和方差的问题,希望你能对它们有一个更深入的理解,并且也能弄清楚怎样评价一个学习算法,能够判断一个算法是偏差还是方差有问题,因为这个问题对于弄清如何改进学习算法的效果非常重要,高偏差和高方差的问题基本上来说是欠拟合和过拟合的问题.
我们用射箭来理解偏差和方差:偏差小代表射箭准,方差小代表射箭稳.结合下面图理解,欠拟合就是高偏差.
我们通常会通过将训练集和交叉验证集的代价函数误差与多项式的次数绘制在同一张图表上来帮助分析:
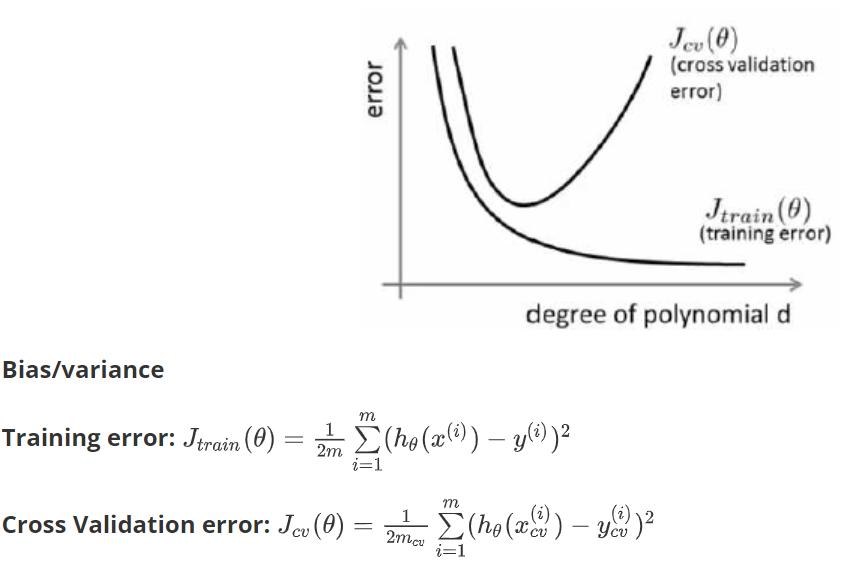
对于训练集,当\(d\)较小时,模型拟合程度更低,误差较大;随着 \(d\)的增长,拟合程度提高,误差减小.对于交叉验证集,当\(d\)较小时,模型拟合程度低,误差较大.但是随着\(d\)的增长,误差呈现先减小后增大的趋势,转折点是我们的模型开始过拟合训练数据集的时候.(虽然它们的计算公式类似,但是集合里的数据是不一样的,所以图像也不一样).
那么,如果我们的交叉验证集(或者训练集)误差较大,我们如何判断是方差还是偏差的问题呢?
对于交叉验证集误差较大的情况,对应于曲线的左右两边,而曲线的左边就是高偏差问题,右边就是高方差问题.
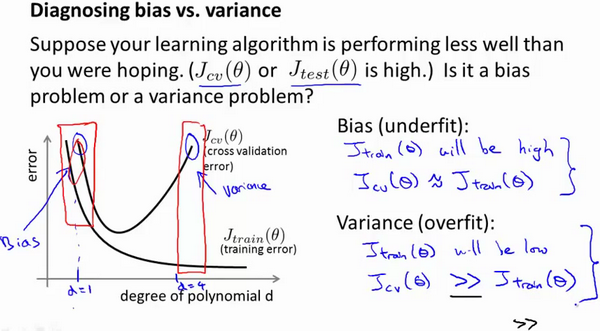
训练集误差和交叉验证集误差近似时(且都比较大):偏差/欠拟合
交叉验证集误差远大于训练集误差时:方差/过拟合
9.5 正则化和偏差/方差
在我们在训练模型的过程中,一般会使用一些正则化方法来防止过拟合.但是我们可能会正则化的程度太高或太小了,即我们在选择λ的值时也需要思考与刚才选择多项式模型次数类似的问题.
假设我们用如下函数拟合数据:
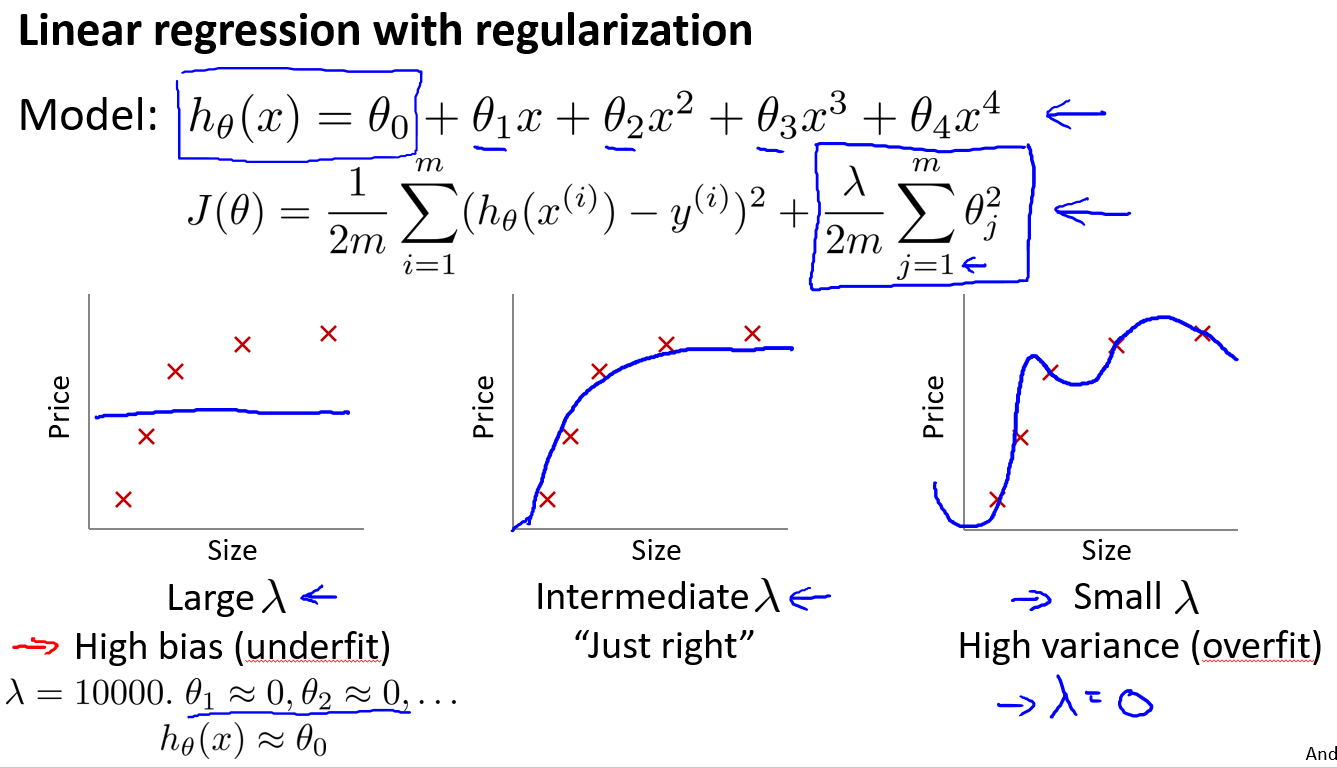
考虑三种\(\lambda\)的情况,当\(\lambda\)很大时,\(\theta\)相当于只有\(\theta_0\),那么\(h(x)\)相当于常数,这就是高偏差欠拟合的情况.同理\(\lambda\)很大时,相当于没有正则化,就是高方差过拟合的情况.
我们选择一系列的想要测试的\(\lambda\)值,通常是 0-10之间的呈现2倍关系的值(如:0,0.01,0.02,0.04,0.08,0.15,0.32,0.64,1.28,2.56,5.12,10.24共12个).我们同样把数据分为训练集、交叉验证集和测试集.
选择\(\lambda\)的方法为:
- 使用训练集训练出12个不同程度正则化的模型
- 用12个模型分别对交叉验证集计算的出交叉验证误差
- 选择得出交叉验证误差最小的模型
- 运用步骤3中选出模型对测试集计算得出推广误差,我们也可以同时将训练集和交叉验证集模型的代价函数误差与λ的值绘制在一张图表上:
这里我们注意一下图里的一点,训练误差、交叉验证集误差都不包括正则化那一项,但是代价函数包括.
• 当\(\lambda\)较小时,训练集误差较小(过拟合)而交叉验证集误差较大 .
• 随着\(\lambda\)的增加,训练集误差不断增加(欠拟合),而交叉验证集误差则是先减小后增加.
9.6 学习曲线
学习曲线就是一种很好的工具,我经常使用学习曲线来判断某一个学习算法是否处于偏差、方差问题.
学习曲线是学习算法的一个很好的合理检验(sanity check).学习曲线是将训练集误差和交叉验证集误差作为训练集样本数量(m)的函数绘制的图表.即,如果我们有100行数据,我们从1行数据开始,逐渐学习更多行的数据.它的思想是:当训练较少行数据的时候,训练的模型将能够非常完美地适应较少的训练数据,但是训练出来的模型却不能很好地适应交叉验证集数据或测试集数据.
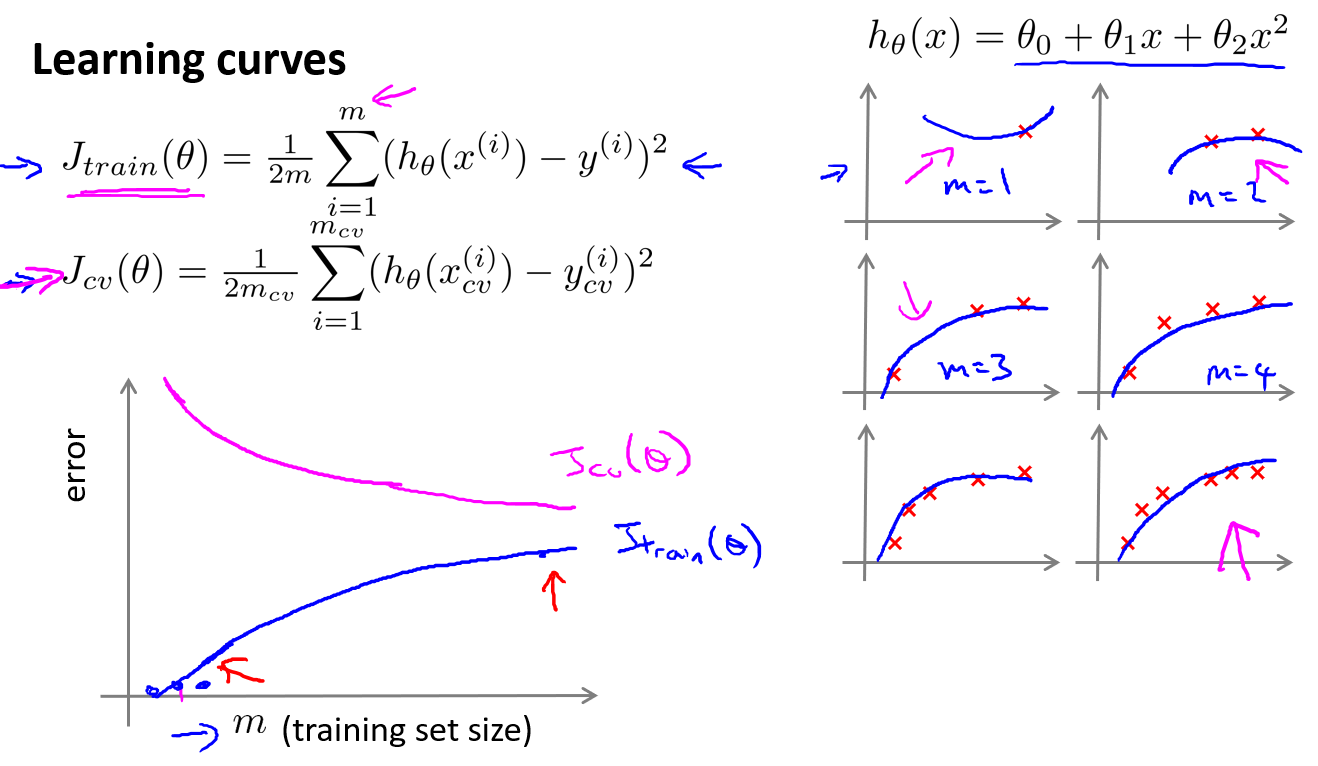
如何利用学习曲线识别高偏差/欠拟合:作为例子,我们尝试用一条直线来适应下面的数据,可以看出,当样本少的时候,训练集误差小,验证集误差大,而样本多的时候两者相近.还有一点是,当样本多的时候,即使它们趋于一致,也是趋于一个很大的值.
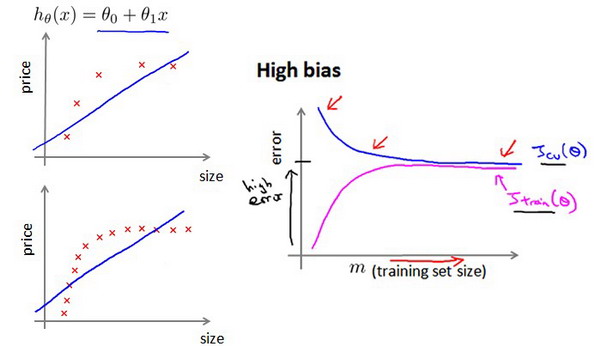
可以得出规律,当学习算法处于高偏差问题时,当样本增大,验证集误差变化曲线基本变平了(因为得到的算法公式基本与之前一致).
如何利用学习曲线识别高方差/过拟合:假设我们使用一个非常高次的多项式模型,并且正则化非常小,可以看出,当交叉验证集误差远大于训练集误差时,往训练集增加更多数据可以提高模型的效果.
高方差的主要特点就是交叉验证集误差远大于训练集误差.还有一点就是:在高方差/过拟合的情况下,增加更多数据到训练集可能可以提高算法效果.
9.7 决定下一步做什么
我们已经介绍了怎样评价一个学习算法,我们讨论了模型选择问题,偏差和方差的问题.那么这些诊断法则怎样帮助我们判断,哪些方法可能有助于改进学习算法的效果,而哪些可能是徒劳的呢?
让我们再次回到最开始的例子,我们试图用正则化线性回归模型拟合数据,发现没有到达预期的效果.我们提出来以下方法,怎么判断哪些方法有效呢?
1.获得更多的训练样本——解决高方差(至少先画出学习曲线,发现有高方差问题)
2.尝试减少特征的数量——解决高方差(一定要先发现有高方差再试图减少,不然是浪费时间)
3.尝试获得更多的特征——解决高偏差
4.尝试增加多项式特征——解决高偏差
5.尝试减少正则化程度λ——解决高偏差
6.尝试增加正则化程度λ——解决高方差
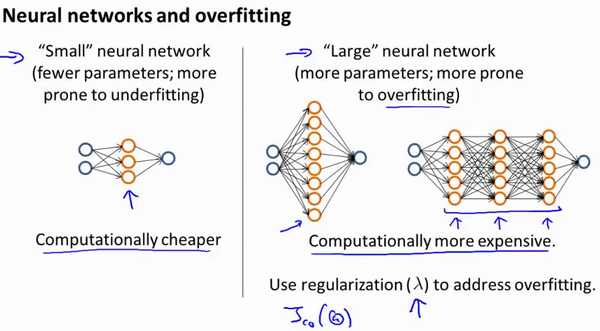
下面介绍一些经验:如何选择神经网络的结构.
使用较小的神经网络,类似于参数较少的情况,容易导致高偏差和欠拟合,但计算代价较小.使用较大的神经网络,类似于参数较多的情况,容易导致高方差和过拟合,虽然计算代价比较大,但是可以通过正则化手段来调整而更加适应数据.
通常选择较大的神经网络并采用正则化处理会比采用较小的神经网络效果要好.对于神经网络中的隐藏层的层数的选择,通常从一层开始逐渐增加层数,为了更好地作选择,可以把数据分为训练集、交叉验证集和测试集,针对不同隐藏层层数的神经网络训练神经网络,然后选择交叉验证集代价最小的神经网络.(测试误差是衡量模型对新样本泛化能力,能不能对新样本做出好的预测.)
