机器学习 吴恩达 第七章 笔记
七、神经网络:表述(Neural Networks: Representation)
7.1 非线性假设
&emsp假设有一个监督学习的训练集如下所示:
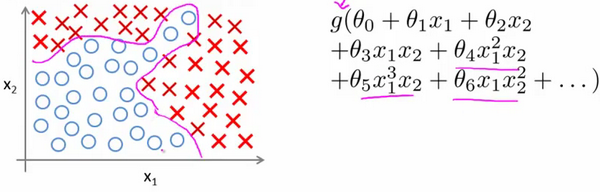
如果我们用逻辑回归来解决问题,可能需要构造多个高次多项式.但这只是有两个特征的情况.如果有多个特征,即使只有二次多项式,最后也会有很多项.这对于一般的逻辑回归来说,要计算的项太多了.
当然我们也可有尝试只包含上面二次多项式的子集,但是这样会造成忽略太多相关数据,当拟合的时候可能不会有很好的效果.所以当特征数量很多时,建立非线性分类器不是一个明智的做法.
机器学习许多问题特征数量都有很多.假设我们希望训练一个模型来识别视觉对象(例如识别一张图片上是否是一辆汽车),我们怎样才能这么做呢?实际上计算机识别图片是识别图片的一个个像素,最后一张图片会构成像素矩阵.

我们要构造一个汽车识别模型,我们要做的就是得到两种训练集,一种都是车,另一些都不是,然后就可以把样本输入给学习算法以训练出一个分类器,并且我们要利用图片上一个个像素的值(饱和度或亮度)来作为特征:
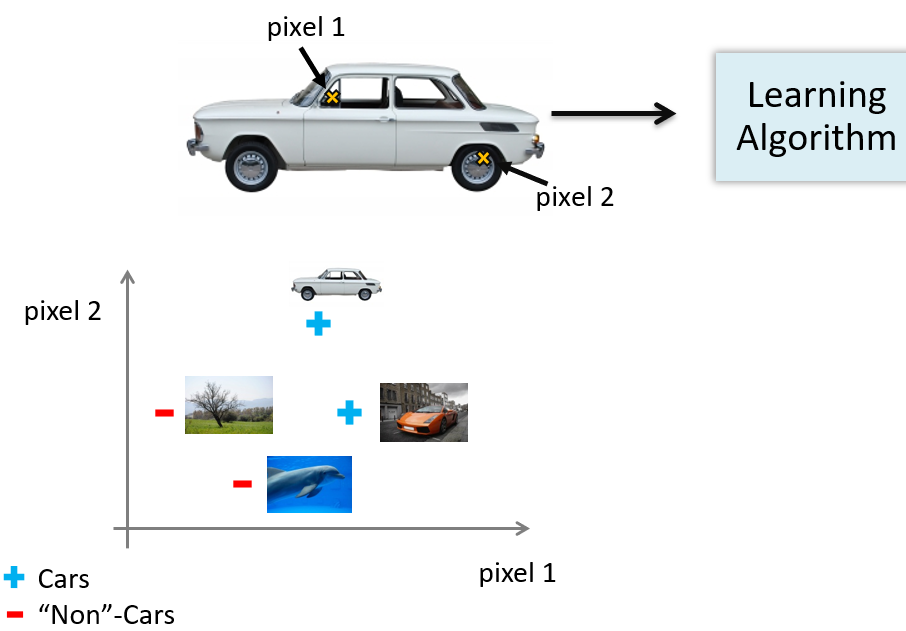
比如上图就是将\(pixel1\)和\(pixel 2\)作为特征,我们在坐标轴上标出车和非车的位置,最后会发现车和非车分布在图像的不同区域.因此我们就需要一个非线性假设来分开这两类样本.
假使我们采用的都是50x50像素的小图片,并且我们将所有的像素视为特征,则会有2500个特征,如果我们要进一步将两两特征组合构成一个多项式模型,则会有约\(\frac{2500^2}{2}\)(接近300,0000个)特征(而这只是一个样本).普通的逻辑回归模型,不能有效地处理这么多的特征,这时候我们需要神经网络,它在学习复杂的非线性假设上被证明是好得多的算法,即使\(n\)特征个数很大时也能轻松搞定.
7.2 神经元和大脑
神经网络是一种很古老的算法,它最初产生的目的是制造能模拟大脑的机器.
我们能学习数学,学着做微积分,而且大脑能处理各种不同的令人惊奇的事情.似乎如果你想要模仿它,你得写很多不同的软件来模拟所有这些五花八门的奇妙的事情.不过能不能假设大脑做所有这些,不同事情的方法,不需要用上千个不同的程序去实现.相反的,大脑处理的方法,只需要一个单一的学习算法就可以了.尽管这只是一个假设,但也有相关的证据.
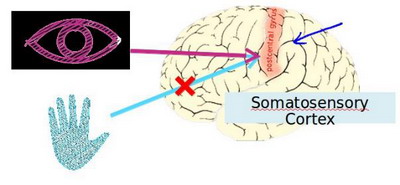
大脑的这一部分这一小片红色区域是你的听觉皮层,你现在正在理解我的话,这靠的是耳朵.耳朵接收到声音信号,并把声音信号传递给你的听觉皮层.正因如此,你才能明白我的话.
神经系统科学家做了下面这个有趣的实验,把耳朵到听觉皮层的神经切断.在这种情况下,将其重新接到一个动物的大脑上,这样从眼睛到视神经的信号最终将传到听觉皮层.如果这样做了,那么结果表明听觉皮层将会学会'看'.这里的'看'代表了我们所知道的每层含义.所以,如果你对动物这样做,那么动物就可以完成视觉辨别任务,它们可以看图像,并根据图像做出适当的决定.它们正是通过脑组织中的这个部分完成的.下面再举另一个例子,这块红色的脑组织是你的躯体感觉皮层,是你用来处理触觉的,如果你做一个和刚才类似的重接实验,那么躯体感觉皮层也能学会'看'.这个实验和其它一些类似的实验,被称为神经重接实验.从这个意义上说,如果人体有同一块脑组织可以处理光、声或触觉信号,那么也许存在一种学习算法,可以同时处理视觉、听觉和触觉,而不是需要运行上千个不同的程序,或者上千个不同的算法来做这些大脑所完成的成千上万的美好事情.也许我们需要做的就是找出一些近似的或实际的大脑学习算法,然后实现它大脑通过自学掌握如何处理这些不同类型的数据.在很大的程度上,可以猜想如果我们把几乎任何一种传感器接入到大脑的几乎任何一个部位的话,大脑就会学会处理它.
下面再举几个例子:
这张图是用舌头学会'看'的一个例子.它的原理是:这实际上是一个名为BrainPort的系统,它现在正在FDA(美国食品和药物管理局)的临床试验阶段,它能帮助失明人士看见事物.它的原理是,你在前额上带一个灰度摄像头,面朝前,它就能获取你面前事物的低分辨率的灰度图像.你连一根线到舌头上安装的电极阵列上,那么每个像素都被映射到你舌头的某个位置上,可能电压值高的点对应一个暗像素,电压值低的点对应于亮像素.依靠它现在的功能,使用这种系统就能让你我在几十分钟里就学会用我们的舌头'看'东西.

这是第二个例子,关于人体回声定位或者说人体声纳.你有两种方法可以实现:你可以弹响指,或者咂舌头.不过现在有失明人士,确实在学校里接受这样的培训,并学会解读从环境反弹回来的声波模式—这就是声纳.

如果你在青蛙身上插入第三只眼,青蛙也能学会使用那只眼睛.
如果你能把几乎任何传感器接入到大脑中,大脑的学习算法就能找出学习数据的方法,并处理这些数据.从某种意义上来说,如果我们能找出大脑的学习算法,然后在计算机上执行大脑学习算法或与之相似的算法,也许这将是我们向人工智能迈进做出的最好的尝试.
7.3 模型表示1
神经网络算法模仿了大脑中的神经元或者神经网络.为了解释如何表示假设模型,让我们先看一下单个神经元在大脑里是什么样的.
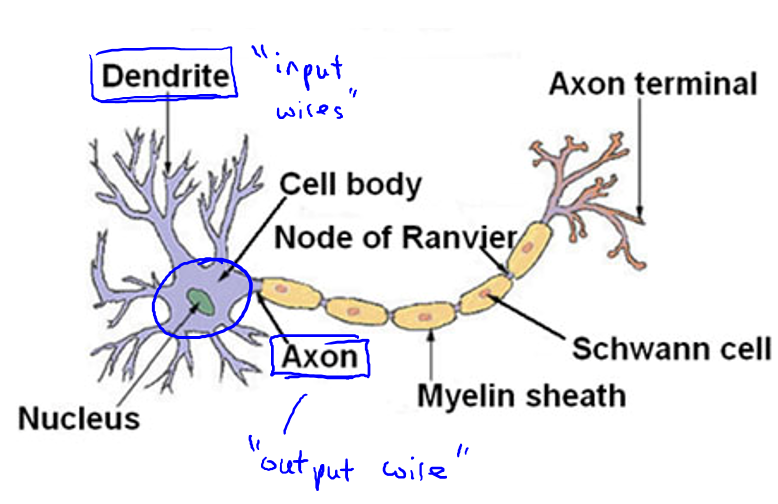
每一个神经元都可以被认为是一个处理单元/神经核(processing unit/Nucleus),它含有许多输入/树突(input/Dendrite),并且有一个输出/轴突(output/Axon).它是一个计算单元,它从树突接收一定数量的信息,并做处理从轴突输出到其他节点.神经网络是大量神经元相互链接并通过电脉冲来交流的一个网络.
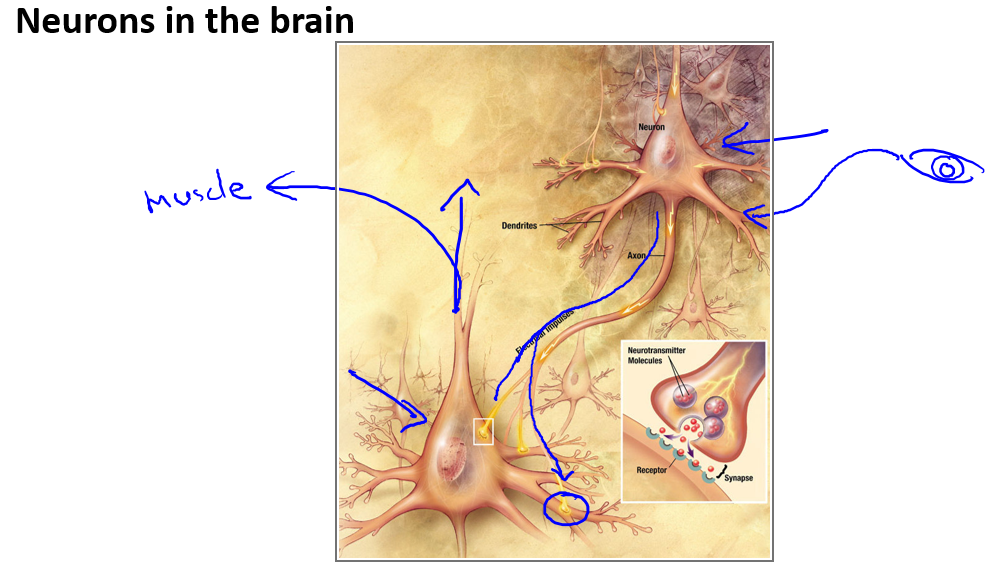
下面是一组神经元的示意图,神经元利用微弱的电流进行沟通.这些弱电流也称作动作电位,其实就是一些微弱的电流.所以如果神经元想要传递一个消息,它就会就通过它的轴突,发送一段微弱电流给其他神经元,这就是轴突.
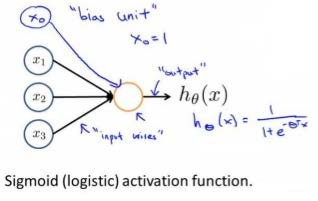
在神经网络或者电脑实现的人工神经网络里,我们用如下模型模拟神经元的工作.下图是用神经网络模拟逻辑回归模型,我们也会称作带有sigmoid或者logistic激活函数的人工神经元.在神经网络的术语中,激活函数是指代非线性函数g(z)的另一种说法.参数又可被称为权重(weight),我们在文献看到的权重和参数是一个东西.其中\(x_1、x_2、x_3\)是输入单元,如果有必要的话,我们有时也会增加一个输入单元\(x_0\),有时也被称作偏置单元和偏置神经元.但\(x_0 = 1\),所以有时不会画出.
上图是单个神经元,而神经网络是一组神经元连接在一起的组合.
其中,\(x_1、x_2、x_3\)是输入单元,我们将原始数据输入给它们.\(a_1、a_2、a_3\)是中间单元,它们负责将数据进行处理,然后呈递到下一层.最后是输出单元,它负责计算\(h_{\theta}(x)\).我们可以在每层都设置一个額外的偏置单元(例如\(x_0\)、\(a_0\)).它的值永远是1.
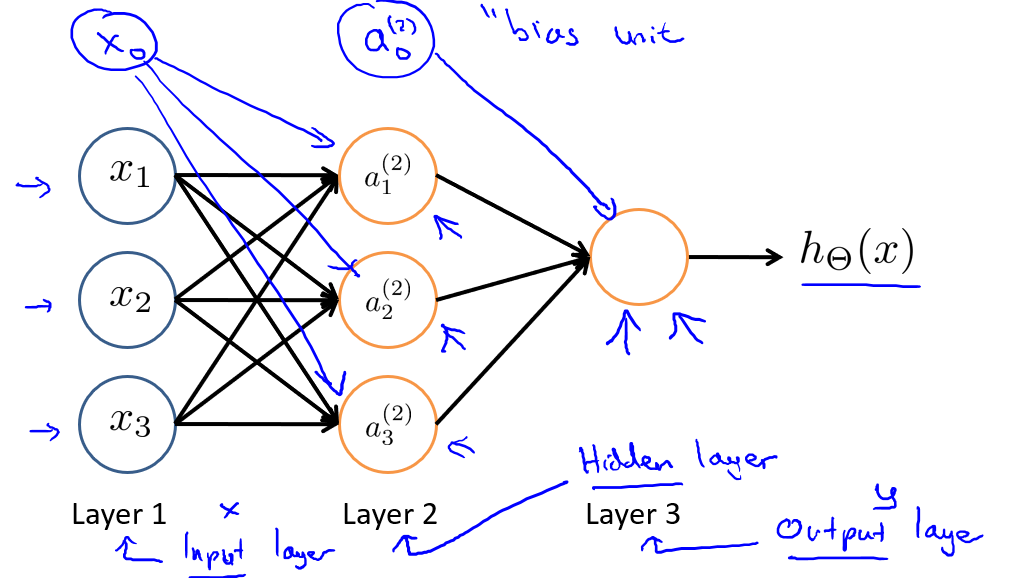
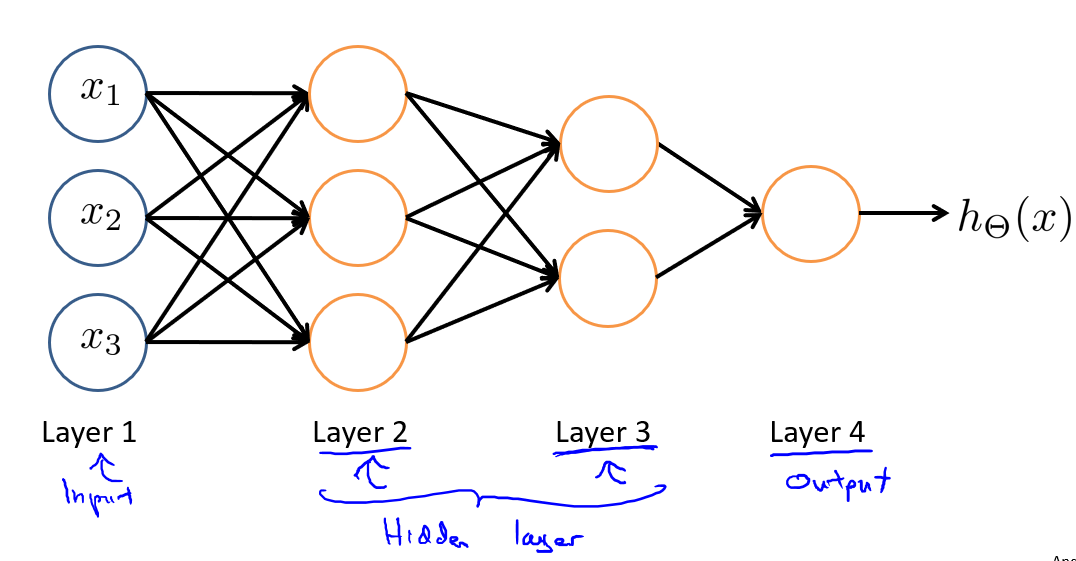
神经网络模型是许多逻辑单元按照不同层级组织起来的网络,每一层的输出变量都是下一层的输入变量.下图为一个3层的神经网络,第一层成为输入层(Input Layer),最后一层称为输出层(Output Layer),中间一层成为隐藏层(Hidden Layers),隐藏层可能不止一个,实际上只要不是输入层和输出层,就被称为隐藏层,它在训练集里不会显示,所以是隐藏的.我们为每一层都增加一个偏差单位(bias unit).
为了理解神经网络的模型,下面引入一些标记法来帮助描述模型:
- \(a_i^{(j)}\):代表第
j层的第i个激活单元 - \(\theta^{(j)}\):代表从第
j层映射到第j+1层时的权重的矩阵.例如\(\theta^{(1)}\)表示从第一层映射到第二层的权重的矩阵.其尺寸为:以第j+1层的激活单元数量为行,以第j层的激活单元数加一为列数的矩阵.下图的\(\theta^{(1)}\)其实是一个3x4的矩阵.(\(x_0\)占了一列,但是\(a_0\)没用输入)
下面是这张图表示的计算:
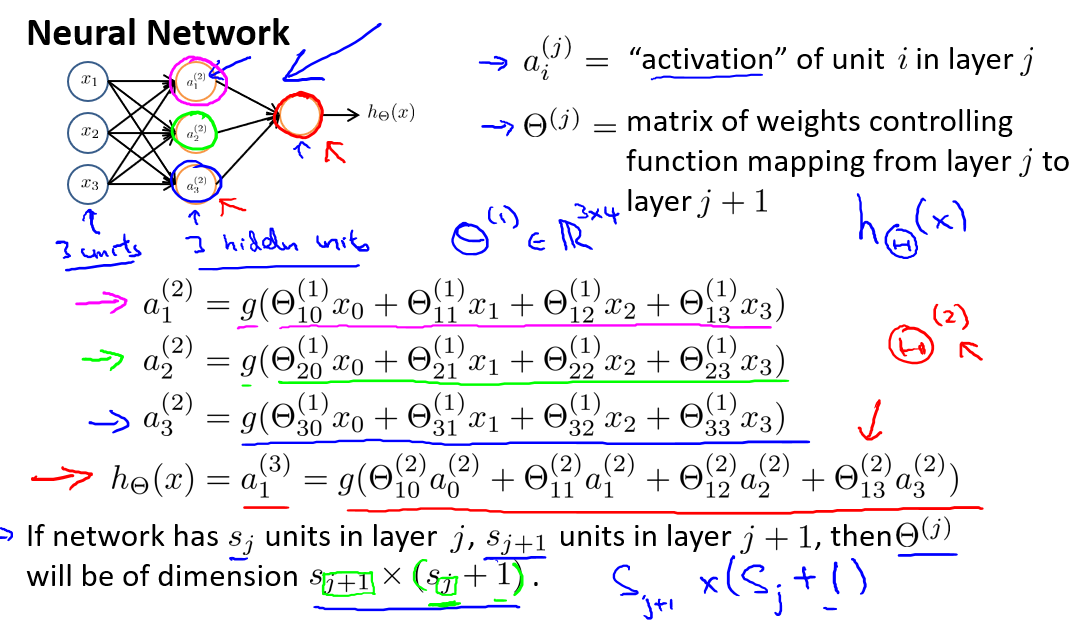
我们来解释一下\(\theta\)的下标什么意思,神经网络中每个连接都有权重:
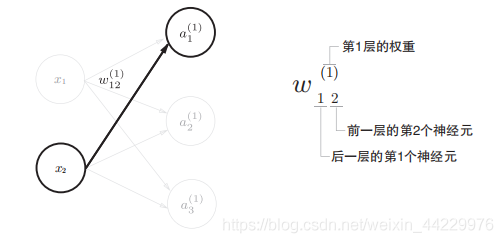
上面进行的讨论中只是将特征矩阵中的一行(一个训练实例)喂给了神经网络,我们需要将整个训练集都喂给我们的神经网络算法来学习模型.
请注意,上面的向量都表现为列向量.
7.4 模型表示2
在上节,我们讲述如何在数学意义计算神经网络的假设函数.在本节,我们讲述如何高效计算,并展示一个向量化的实现方法.
首先,我们定义一些額外的值.我们将\(a_1^{(2)}\) = \(g(z_1^{(2)})\).而\(a_2^{(2)}\)也有类似的定义.也就是\(z\)表示的都是一些线性组合.
接下来以神经网络第二层为例,讲述如何向量化计算\(a^{(2)}\).首先看下面这幅图,我们将\(x\)命名为如下,而\(z^{(2)}\)也如图所示.那么\(z^{2} = \circleddash^{(1)}x\).后面的等式a^{(2)} = g(z^{(2)})实际上是\(g\)也就是S型函数(也称作激活函数)逐个作用于向量\(z^{(2)}\).
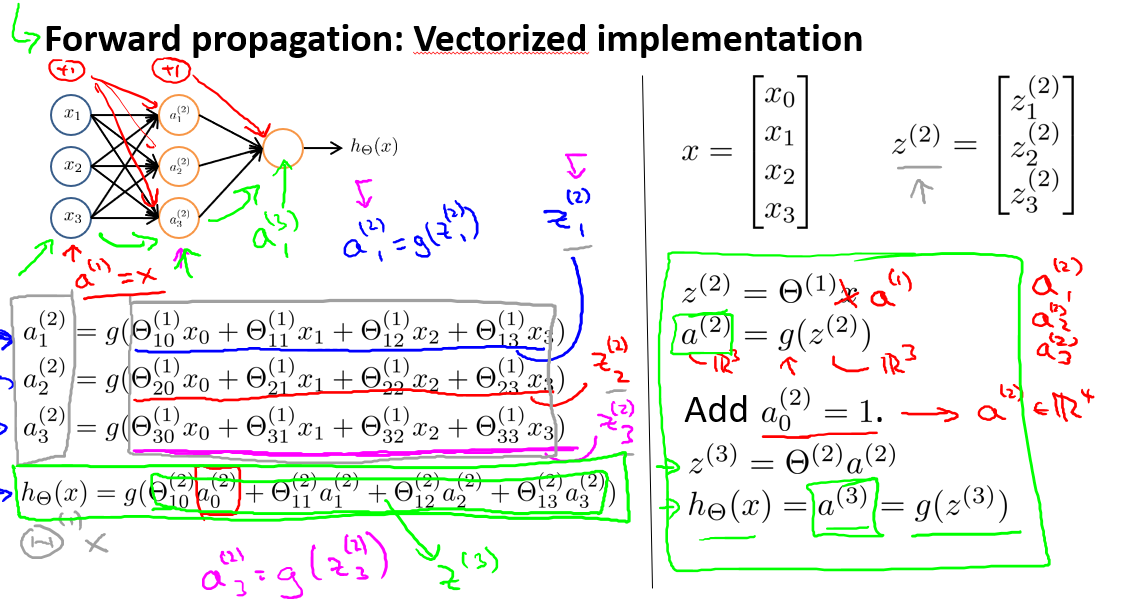
为了方便讲解,我们也把向量\(x\)称作\(a^{(1)}\),所以\(z^{2} = \circleddash^{(1)}x\)也可以改为\(z^{2} = \circleddash^{(1)}a^{(1)}\).
好的,汇总一下,我们以计算神经网络第二层为例,向量化计算方法如下:
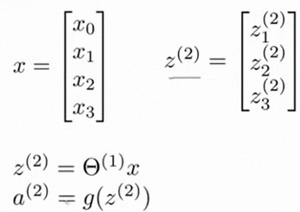
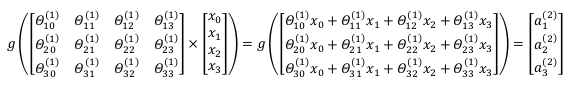
我们令\(z^{(2)} = \theta^{(1)}x\).则\(a^{(2)} = g(z^{(2)})\).计算后添加\(a_2^{(0)} = 1\),计算输出的值为:
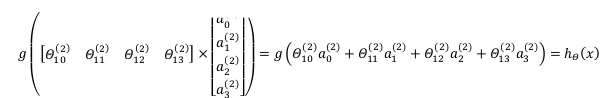
我们令\(z^{(3)} = \theta^{(2)}a^{(2)}\),则\(h_{\theta}(x) = a^{(3)} = g(z^{(3)})\).最后\(h\)输出的是一个实数.但这只是针对训练集中一个训练实例所进行的计算.如果我们要对整个训练集进行计算,我们需要将训练集特征矩阵进行转置,使得同一个实例的特征都在同一列里.即:
这里的\(Z\)不是向量了,而是矩阵.
我们可以知道:每一个\(a\)都是由上一层所有的\(x\)和每一个\(x\)所对应的\(\theta\)决定的.我们把这样从左到右的算法称为前向传播算法( FORWARD PROPAGATION)
为了更好了了解Neuron Networks的工作原理,我们先把左半部分遮住,这看起来很像逻辑回归模型:
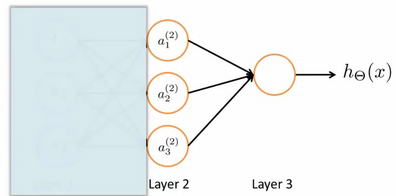
右半部分其实就是以\(a_0,a_1,a_2,a_3\),按照Logistic Regression的方式输出\(h_{\theta}(x)\)
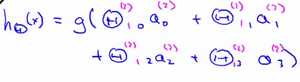
与逻辑回归不同的就是输入的特征\(a_0,a_1,a_2,a_3\),实际是以隐藏层计算得出的.具体可以看下面的解释,比起逻辑回归我们将测试数据喂给算法,神经网络是自己将数据喂给假设算法:

最后,神经网络中神经元连接方式称为神经网络的架构.神经网络中间每层都改变了输入的"特征",最后喂给假设算法可能会得到一些有趣的非线性函数.
7.5 特征和直观理解1
在本节,我们会继续说明神经网络是怎么处理复杂非线性函数的输入的.
从本质上讲,神经网络能够通过学习得出其自身的一系列特征.在普通的逻辑回归中,我们被限制为使用数据中的原始特征\(x_1,x_2,...,x_n\).我们虽然可以使用一些二项式项来组合这些特征,但是我们仍然受到这些原始特征的限制.在神经网络中,原始特征只是输入层,在我们上面三层的神经网络例子中,第三层也就是输出层做出的预测利用的是第二层的特征,而非输入层中的原始特征,我们可以认为第二层中的特征是神经网络通过学习后自己得出的一系列用于预测输出变量的新特征.
神经网络中,单层神经元(无中间层)的计算可用来表示逻辑运算,比如逻辑与(AND)、逻辑或(OR).
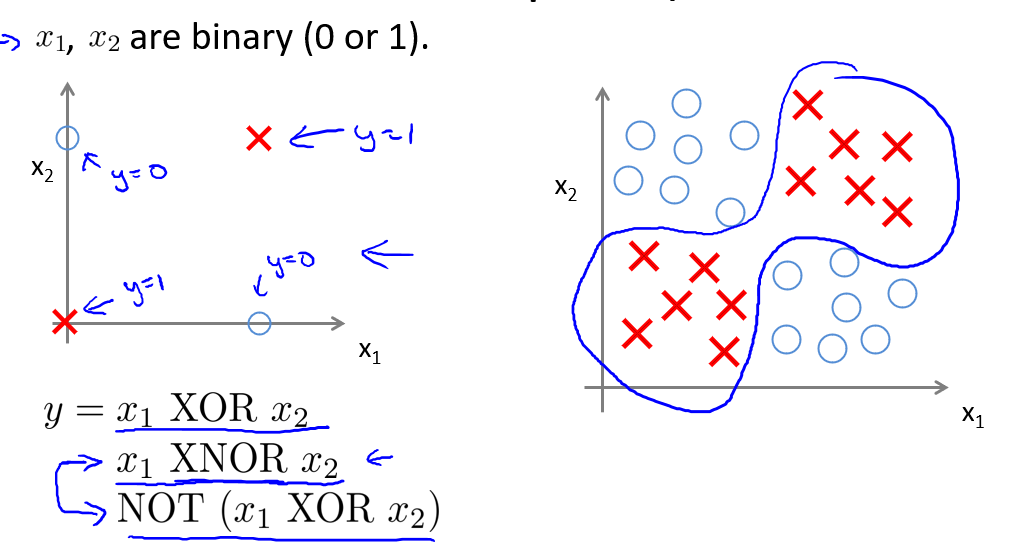
我们举一个例子,我们有\(x_1\)和\(x_2\)两个输入特征,且它们只能取0、1两个值.我们举的例子虽然只有4个样本,但是可以看作右边图的简化版本.我们要做的就是学习一个复杂的非线性边界,来区分正负样本.
具体来说,我们需要建立一个目标函数:\(y = x_1 XOR x_2\)或者\(y = x_1 NXOR x_2\).接下来,我们要建立一个神经网络,拟合这种训练集(因为XNOR更好一点,这里用拟合XNOR运算的神经网络的例子).
为了拟合NXOR的神经网络,我们先从简单的开始,也就是AND运算的神经网络.
如下图,我们有两个输入特征,只能取0和1.目标函数\(y = x_1 AND x_2\).为了拟合拟合这个函数,需要在第一层加入一个偏置单元.随后我们需要对神经网络之间的连接的权重进行赋值.赋值情况如下图,表示我们的假设函数是\(h_{\theta}(x) = g(-30+20x_1+20x_2)\)
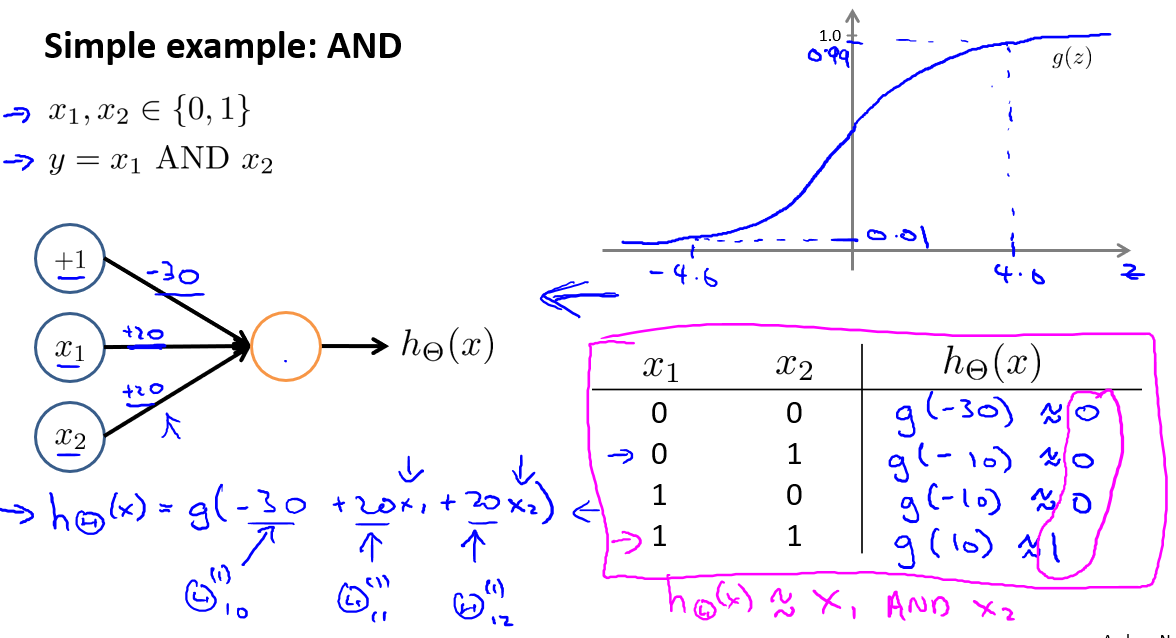
配合\(g(z)\)函数,我们来了解一下到底什么意义.上图的表是\(x_1、x_2\)不同取值时,假设函数的情况.我们可以发现当取不同值时,\(h\)对应的结果刚好是逻辑\(AND\)的结果.所以\(h_{\theta}(x)\)近似等于\(AND\).

下面这张图可以实现逻辑或.将假设函数写出来即可.

7.5 样本和直观理解II
本节继续讲解神经网络如何处理复杂的非线性假设模型的.
二元逻辑运算符(BINARY LOGICAL OPERATORS)当输入特征为布尔值(0或1)时,我们可以用一个单一的激活层可以作为二元逻辑运算符,为了表示不同的运算符,我们只需要选择不同的权重即可.
下图的神经元(两个权重分别为10,-20)可以被视为作用等同于逻辑非(NOT):
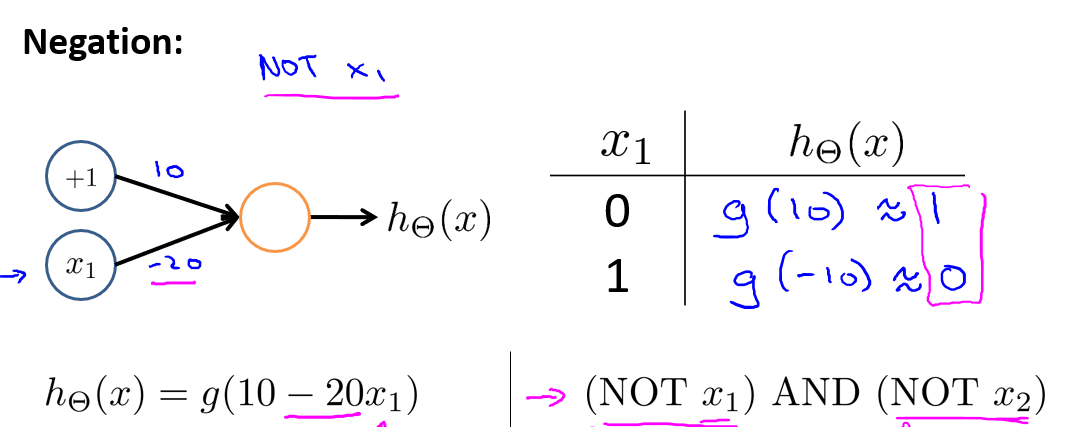
我们可以利用神经元来组合成更为复杂的神经网络以实现更复杂的运算.例如我们要实现XNOR功能(输入的两个值必须一样,均为1或均为0).即
我们可以看出\(XNOR\)是多个神经元的组合.因此先构造\((NOT x_1)AND(NOT x_2)\)神经元:
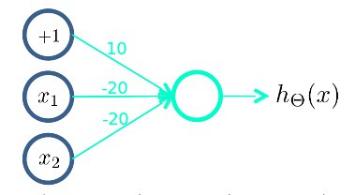
再将它们放在一起,我们就得到了一个能实现 NXOR的神经网络,这样我们也形成了一条非线性边界:
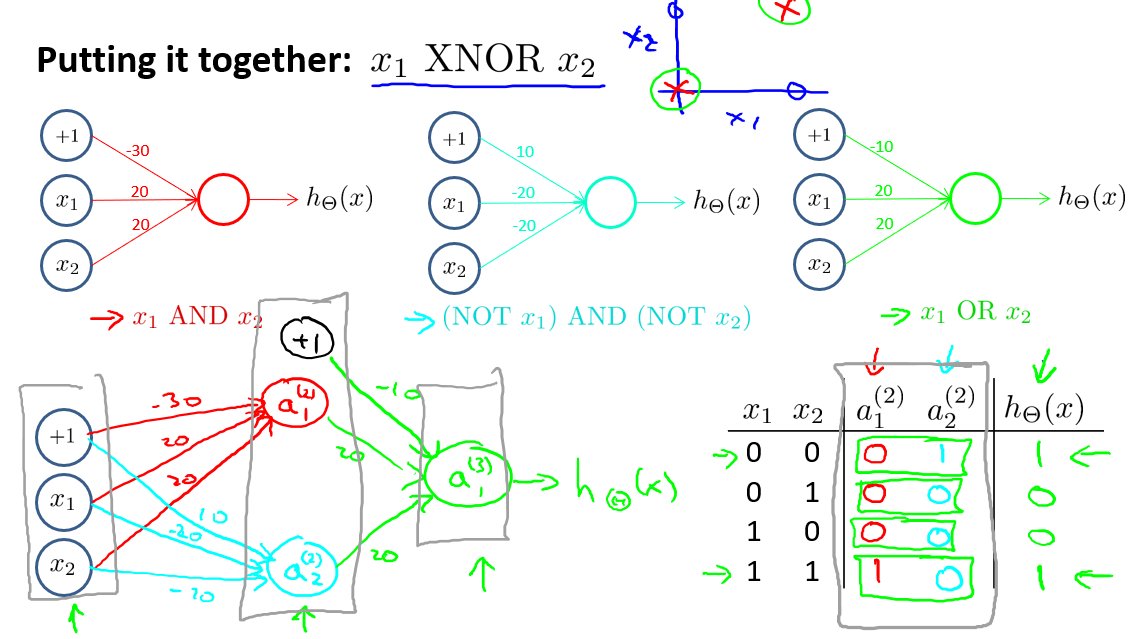
按这种方法我们可以逐渐构造出越来越复杂的函数,也能得到更加厉害的特征值.
7.7 多类分类
本节讲述神经网络如何实现多分类.
神经网络实现多类别实际是一对多的扩展.如果我们要训练一个神经网络算法来识别路人、汽车、摩托车和卡车,在输出层我们应该有4个值.例如,第一个值为1或0用于预测是否是行人,第二个值用于判断是否为汽车.这样的化,我们就要建立有4个输出单元的神经网络(也可说是4维向量).
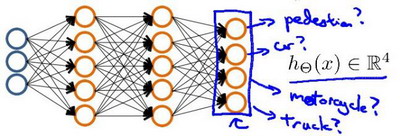
下面是不同类别的输出情况:
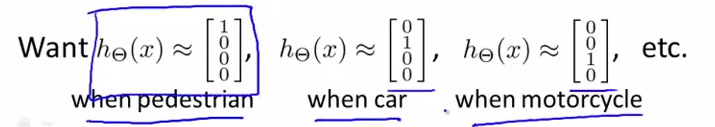
这很像逻辑回归分类的情景,4个输出单元类似4个逻辑回归分类器.
而本模型的训练集可能是如下形式,我们要做的就是找到这样的\(h\)输出这些值: