机器学习 吴恩达 第五章 笔记
五、逻辑回归(Logistic Regression)
5.1 分类问题
在接下来的几节里,我想讨论要预测的变量\(y\)是一个离散值的分类问题.接下来就是讨论逻辑回归算法.
在分类问题中,我们尝试预测的是结果是否属于某一个类(例如正确或错误).分类问题的例子有:判断一封电子邮件是否是垃圾邮件;判断一次金融交易是否是欺诈;之前我们也谈到了肿瘤分类问题的例子,区别一个肿瘤是恶性的还是良性的.
我们从二元的分类问题开始讨论:
我们将\(y\)的范围确定是属于{0,1}两个数.我们常常用0表示没有某种属性,而1表示有我们要寻找的属性.
我们将因变量(dependent variable)可能属于的两个类分别称为负向类(negative class)和正向类(positive class),则因变量\(y \in 0,1\).其中0表示负向类,1表示正向类.
如果我们要用线性回归算法来解决一个分类问题,我们会想到用一条直线取拟合数据.如果想要作出预测,一个做法是设置一个阈值,如果＞阈值,我们设置为正类(如下所示),小于阈值设置为反类.
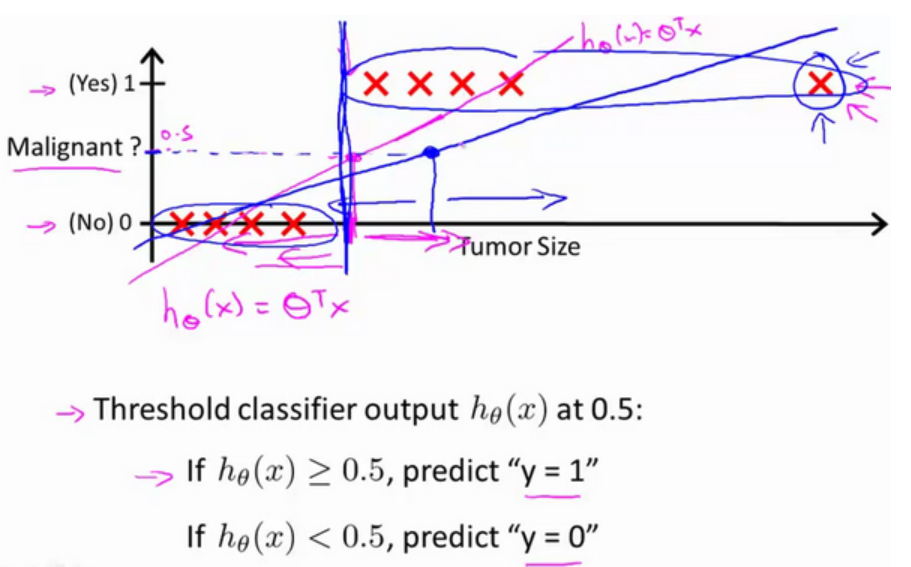
在上图预测肿瘤性质的例子里,线性回归的预测效果似乎还可以.但如果我们把横轴延长一点,假设有另一个训练样本位于右方远处,如果在此样本运行线性回归,就会得到另外一条直线(蓝色)去拟合数据.如果阈值没有改变(仍为$ h_{\theta}(x) = 0.5$),这样的拟合效果就比较差劲.在右方远处的样本没有提供什么有用的信息,但它使得拟合效果不佳.所以考虑到上述问题,将线性回归用于分类问题,通常不是一个好主意.
接下来再思考一个问题,如果我们将线性回归用于分类问题会怎么样?对于分类,y取值0或1.但如果你使用的是线性回归,那么假设函数的输出值可能远大于1,或者远小于0.即使所有训练样本的标签y都等于0或等于1.尽管我们知道y应该取值0 或者1,但是如果算法得到的值远大于1或者远小于0的话，就会感觉很奇怪.在后面几节,我们将介绍逻辑回归算法,这个算法的性质是:它的输出值永远在0到1之间.
5.2 假设陈述
在本节,我要给你展示假设函数的表达式,也就是说,在分类问题中,要用什么样的函数来表示我们的假设.此前我们说过,希望我们的分类器的输出值在0和1之间.因此,我们希望想出一个满足某个性质的假设函数,这个性质是它的预测值要在0和1之间.
当我们使用线性回归时,假设看起来是这样:
这里我们打算修改一点来获得逻辑回归函数,也就是把\(\theta^Tx\)当作g函数(逻辑函数 logistic function)的参数.即:
逻辑函数也称为\(S\)形函数(Sigmoid function),如果我们将\(z = \theta^TX\),那么:
如果我们将上面两式联立的话,就会得到:
科普一下:sigmoid函数可以将一个实数映射到[0,1]的区间,可以用来做二分类.
该函数的图像为:
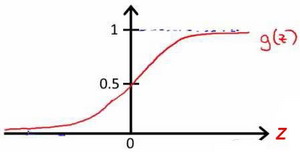
我们需要用参数\(\theta\)来拟合我们的数据.所以拿到训练集时,我们需要给参数\(\theta\)设定一个值.
稍后我们会学习一个方法,帮助我们拟合参数\(\theta\).但现在我们先讨论对这个模型的解释:
当我们的假设\(h_{\theta}(x)\)输出一个数,我们会把它当作,对于一个输入\(x\),y输出1的概率估计.
例如,如果对于给定的\(x\),通过已经确定的参数计算得出$ h_{\theta}(x) = 0.7$.则表示有70%的几率,y为正向类.相应地,y为负向类的几率为1-0.7=0.3.
用数学的方法表示就是
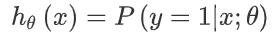
这里解释一下\(P(y=1|x;\theta)\)是什么意思.我们可以参考正态分布的概率密度函数.
.这个函数里有两个参数,均值\(\mu\)和方差\(\sigma\).通过调节这两个参数的取值,我们可以得到不一样的正态分布.以这个概率密度函数也可以用\(f_x(x; \mu , \sigma )\)表示.
5.3 决策界限
本节我们来讲述一下决策界限(decision boundary)的概念.这个概念能更好地帮助我们理解逻辑回归的假设函数在计算什么.
首先我们来思考什么时候y判断为1,什么时候判断为0.之前提过的一个方法:设置阈值,在逻辑回归也同样适用.
当\(h_{\theta}(x) >= 0.5\),预测y=1
当\(h_{\theta}(x) < 0.5\),预测y=0
根据上面绘制出的S形函数图像,我们知道当:
- \(z >= 0\)时,\(g(z) >= 0.5\)
- \(z < 0\)时,\(g(z) < 0.5\)
又因为\(\theta^T x = z\),则转化为\(\theta^T >= 0\)时,预测\(y = 1\).\(\theta^T < 0\)时,预测\(y = 0\).这些有助于我们理解逻辑回归是怎么预测的.
现在假设我们有一个模型和训练集(从这里可以看出\(g\)的参数是不固定的,但是\(g\)是将参数的值映射到[0,1]区间):
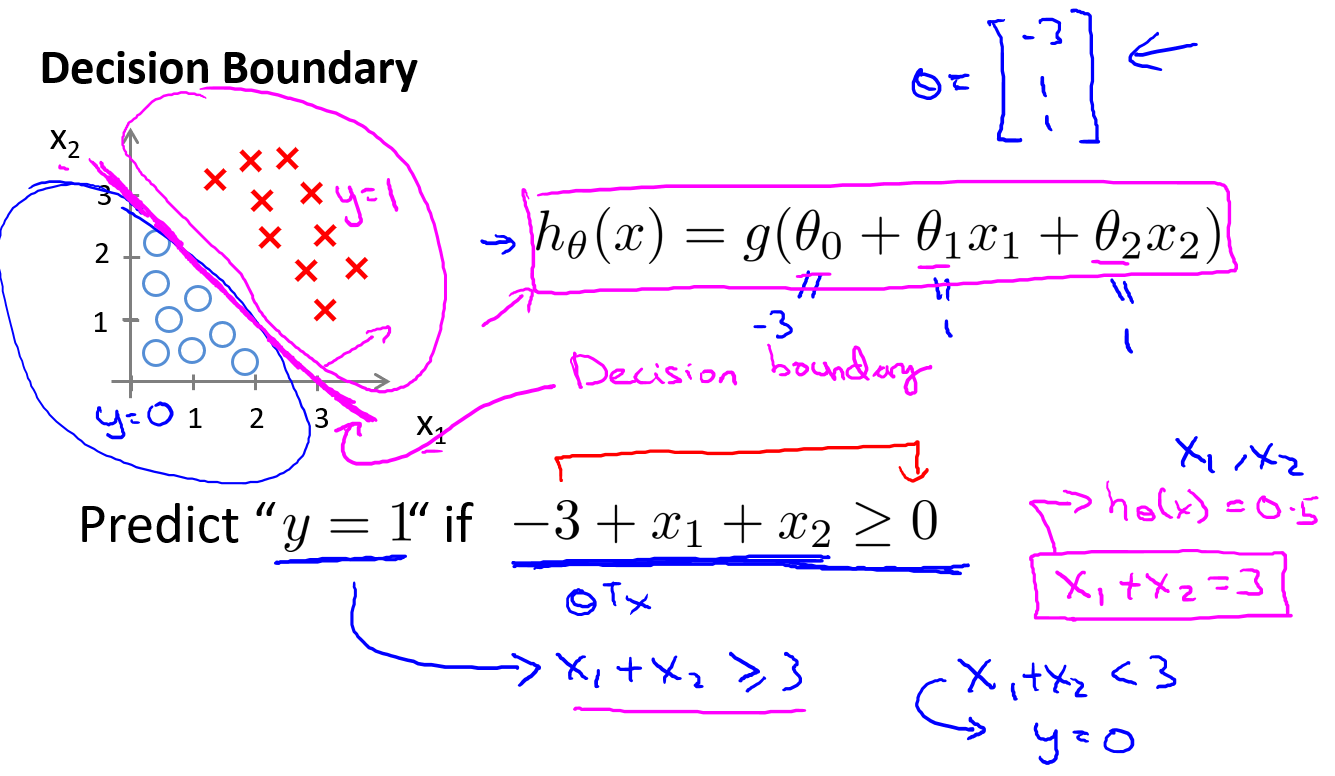
因为我们这里还没讨论如何拟合这里的参数,这里就先假设我们已经拟合好了参数.假设\(\theta_0 = -3,\theta_1=1,\theta_2=1\).有了这些,我们可以构成参数向量.既然有了参数,接下来就是预测什么时候将y预测为1.
使用我们在之前讨论的\(g(z) = 0.5\)的分界点,我们可以发现\(y=1\)当且仅当\(-3+x_1+x_2 >= 0\).我们将不等式变动一下,可以得到:
时,模型认为该样本更有可能是正类.这在图上表示为一条直线.很明显直线划分出了y=1和y=0的区域.我们也把这条线称作决策边界.顺便说明一下,决策边界是假设函数的一个属性,它们由假设函数的参数决定,而不是数据集.当然,我们后续会讨论如何用数据集拟合参数\(\theta\).
现在,来看一个更复杂的例子:
&esmp;假使我们的数据呈现这样的分布情况,怎样的模型才能适合呢?
之前,我们在学习线性回归的时候也学习了多项式回归,将低阶替换为高阶,这里也是同样的做法.
具体来说,我们将假设函数设置成如上,我们添加了額外的两个特征:\(x_1^2\)和\(x_2^2\).这里同样已经求了参数\(\theta\),具体值如上.则我们得到的决策边界恰好是圆点在原点且半径为1的圆形.
通过在特征里增加高阶多项式,我们可以得到更复杂的决策边界.
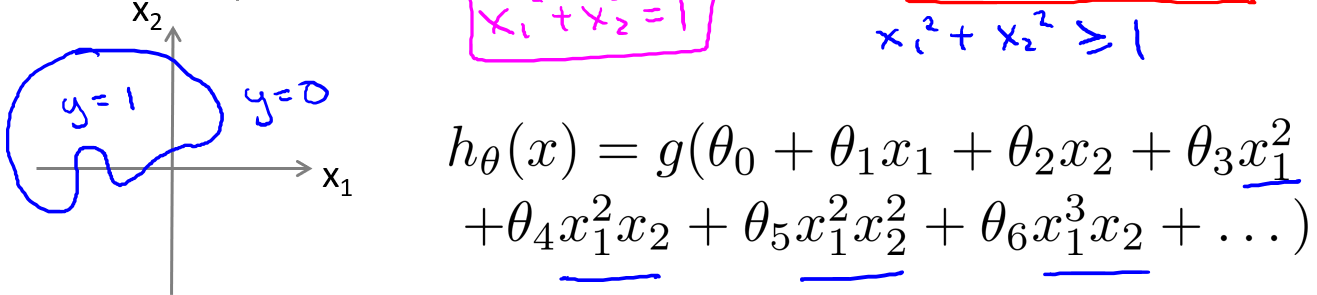
我们可以用非常复杂的模型来适应非常复杂形状的判定边界
5.4 代价函数
在本节,我们要介绍如何拟合逻辑回归模型的参数\(\theta\).具体来说,我要定义用来拟合参数的优化目标或者叫代价函数,这便是监督学习问题中的逻辑回归模型的拟合问题.
理解:什么是拟合?拟合是一种数据处理的方式,不特指哪种方法.简单的说就是你有一组数据,觉得这组数据和一个已知的函数(这个函数的参数未定)很相似,为了得到最能表示这组数据特征的这个函数,通过拟合这种方式(具体的数学方法很多)求得参数Click
从上图给出的mx(n+1)的训练集,我们要找到方法拟合参数\(\theta\).
之前我们讨论线性回归问题时,使用了这个函数:
现在我们要对这个成本函数做一点小变动.我们将\(\frac12\)挪到\(\sum_{i=1}^m\)里面.这样\(\sum\)外面只有一个\(\frac1m\),为了方便,我们将\(\sum\)里的所有命名为\(cost(h_{\theta}(x^{(i)}),y^{(i)})\).那么最后就变成了这样:
我们可以去掉上标为了简便表示(因为实际运算是向量?)在线性回归里我们需要最小化代价函数.在逻辑回归里我们也需要最小化\(cost\).
对于线性回归模型,我们定义的代价函数是所有模型误差的平方和.理论上来说,我们也可以对逻辑回归模型沿用这个定义,但是问题在于,当我们将\(h_{\theta}(x) = \frac1{1+e^{-\theta^Tx}}\)带入到这样定义了的代价函数中时，我们得到的代价函数将是一个非凸函数.
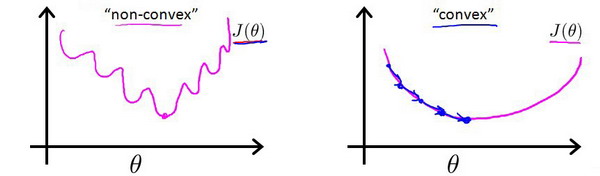
这意味着我们的代价函数有许多局部最小值,这将影响梯度下降算法寻找全局最小值的效率.所以我们要做的就是重新找一个\(cost\)函数,它不像\(cost(h_{\theta}(x^{(i)}),y^{(i)})=\frac12(h_{\theta}(x^{(i)})-y^{(i)})^2\)是一个非凸函数,我们要找到一个函数,使得\(h_{\theta}(x) = \frac1{1+e^{-\theta^Tx}}\)代入仍为凸函数.
因此,我们重新定义逻辑回归的代价函数为:
其中:
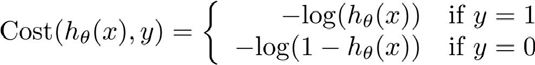
根据函数,我们可以得出\(h_{\theta}(x)\)与\(Cost\)的关系如图:
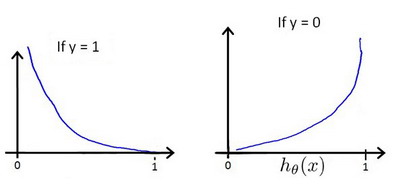
让我们来直观理解一下代价函数\(Cost\).如果样本实际是正类(y=1),而我们的假设函数\(h_{\theta}(x)\)输出也是\(1\)(表示正类的概率100%),这样付出的代价为0.但是如果假设函数输出0,也就是不可能为正类,这会导致Cost的输出非常大.也就是我们要用很大的代价来惩罚我们的代价函数.当\(h\)的输出值越接近\(1\),表示越有可能是正类,这样付出的代价越小.我们可以以同样的思路来理解y=0的图.
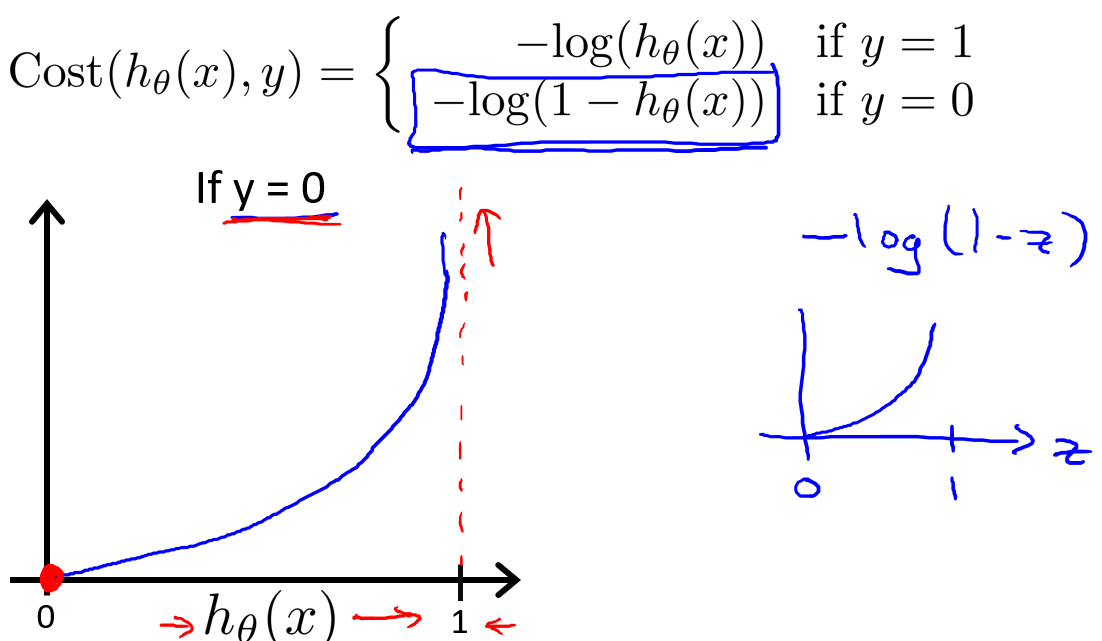
后面我们会将\(Cost\)代入回\(J(\theta)\),利用凸性分析可以发现\(J(\theta)\)是一个凸函数,并且没有局部最优值.但凸性分析的内容是超出这门课的范围的,这里不作细讲.
5.5 简化的成本函数和梯度下降
在本节我们要简化成本函数,以及学习如何使用梯度下降来拟合逻辑回归的参数\(\theta\).
下面是逻辑回归的代价函数:
由于y总是等于1或0,我们有一个简单的方法可以写出代价函数:
我们再将\(Cost\)函数代入回\(J\),可以得到:
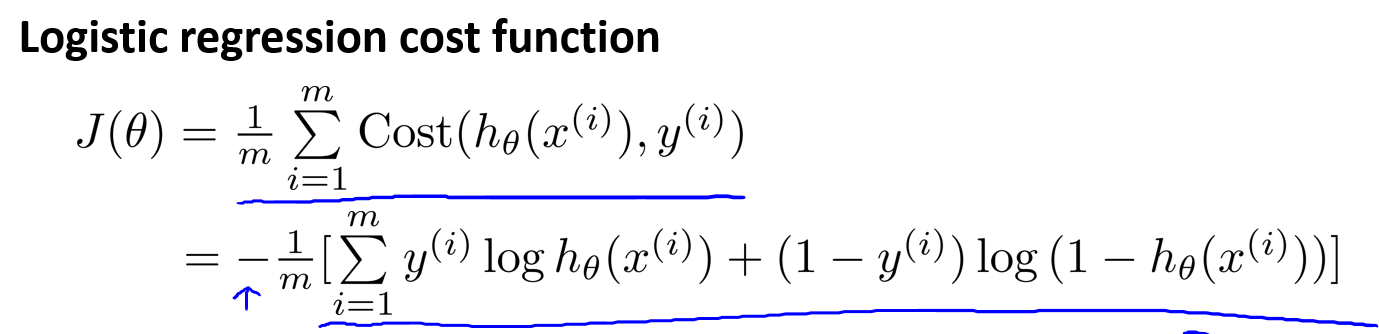
除了这种方式,还有其他方式也能用一行式子表示\(J\)函数.这里不做具体介绍为什么选择这个式子.只是粗略地说明这个式子是由统计学的极大似然估计得出来的.它可以帮助不同模型快速找到参数.而且它还有一个很好的性质,它是凸的.
根据这个代价函数,为了拟合出参数,该怎么做呢?我们要试图找尽量让\(J\)取得最小值的参数\(\theta\).
根据上面的步骤,接下来要考虑的就是如何最小化\(J(\theta)\),这样才能为训练集拟合出参数.最小化代价函数的方法,是使用梯度下降法(gradient descent).这是我们的代价函数:
蓝色笔记部分是求偏导后的结果,我自己在纸上算了是一致的.下面贴下其他佬写的推导过程:
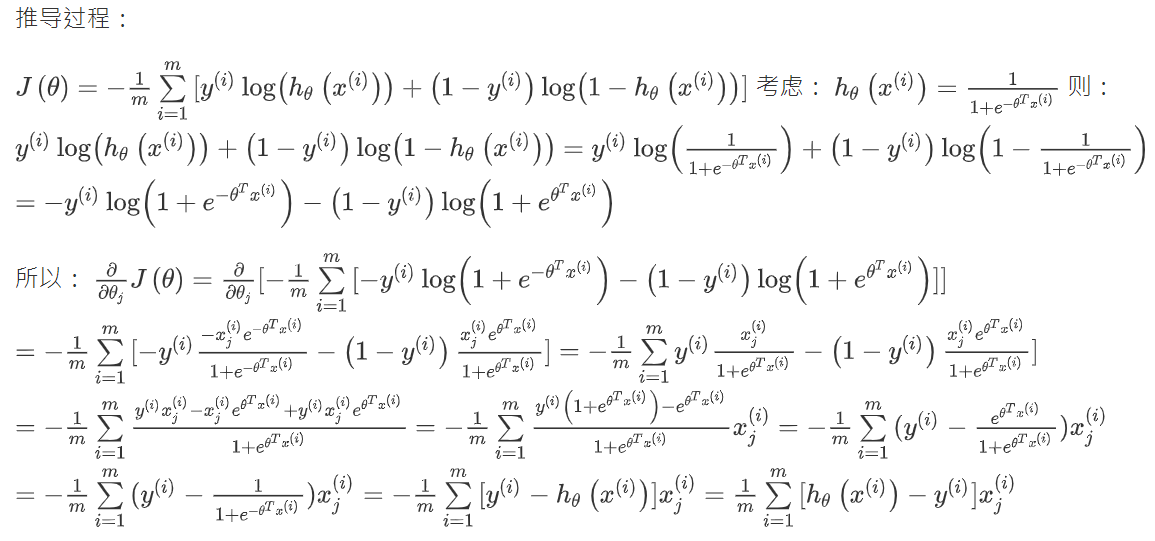
我们将算出来的偏导数带回,就会得到如下结果(图里少了一个\(\frac1m\)):
将\(\theta_j\)的更新规则与之前线性回归的对比,可以发现它与线性回归的式子一模一样.但即使它们的更新规则相同,线性回归和逻辑回归仍然为不同的方法,它们的假设函数也不同.
之前讲线性回归时,检查\(\theta\)收敛的方法也可以用于逻辑回归.
实现迭代更新的一个直接做法就算for循环一个个更新,当然在足够理想的情况下,我们也可以使用矢量化更新.
如何向量化一次性更新\(\theta\)可以参考这个Click
在运行梯度下降算法之前,进行特征缩放依旧是非常必要的.
5.6 高级优化
在上一个视频中,我们讨论了用梯度下降的方法最小化逻辑回归中代价函数\(J(\theta)\).在本次视频中,我会教你们一些高级优化算法和一些高级的优化概念,利用这些方法,我们就能够使通过梯度下降,进行逻辑回归的速度大大提高,而这也将使算法更加适合解决大型的机器学习问题(比如,我们有数目庞大的特征量).
现在我们换个角度来看什么是梯度下降,我们有个代价函数\(J(\theta)\),而我们想要使其最小化,那么我们需要做的是编写代码,当输入参数\(\theta\)时,它们会计算出两样东西:\(J(\theta)\)以及当\(j\)等于0、1直到\(n\)时的偏导数项.
假设我们已经完成了可以实现这两件事的代码,那么梯度下降所做的就是反复执行这些更新.另一种考虑梯度下降的思路是:我们需要写出代码来计算\(J(\theta)\)和这些偏导数,然后把这些插入到梯度下降中,然后它就可以为我们最小化这个函数.于梯度下降来说,我认为从技术上讲,你实际并不需要编写代码来计算代价函数\(J(\theta)\).你只需要编写代码来计算导数项，但是，如果你希望代码还要能够监控这些\(J(\theta)\)的收敛性,那么我们就需要自己编写代码来计算代价函数\(J(\theta)\)和偏导数项.所以,在写完能够计算这两者的代码之后,我们就可以使用梯度下降.然而梯度下降并不是我们可以使用的唯一算法,还有其他一些算法，更高级、更复杂.如果我们能用这些方法来计算代价函数\(J(\theta)\)和偏导数项\(\frac{\partial}{\partial\theta_j} J(\theta)\)两个项的话,那么这些算法就是为我们优化代价函数的不同方法,共轭梯度法 BFGS(变尺度法)和L-BFGS (限制变尺度法)就是其中一些更高级的优化算法,它们需要有一种方法来计算\(J(\theta)\)以及需要一种方法计算导数项,然后使用比梯度下降更复杂的算法来最小化代价函数.这三种算法的具体细节超出了本门课程的范畴.实际上你最后通常会花费很多天,或几周时间研究这些算法,你可以专门学一门课来提高数值计算能力,不过让我来告诉你他们的一些特性:
这三种算法有许多优点:
- 一个是使用这其中任何一个算法,你通常不需要手动选择学习率\(\alpha\).所以对于这些算法的一种理解思路是,给出计算导数项和代价函数的方法,你可以认为算法有一个智能的内部循环尝试多种学习率.而且,事实上,他们确实有一个智能的内部循环,称为线性搜索(
line search)算法,它可以自动尝试不同的学习速率\(\alpha\),并自动选择一个好的学习速率\(\alpha\).因此它甚至可以为每次迭代选择不同的学习速率,那么你就不需要自己选择.这些算法实际上在做更复杂的事情,不仅仅是选择一个好的学习速率,所以它们往往最终比梯度下降收敛得快多了,不过关于它们到底做什么的详细讨论,已经超过了本门课程的范围.
我们实际上完全有可能成功使用这些算法,并应用于许多不同的学习问题,而不需要真正理解这些算法的内环间在做什么,如果说这些算法有缺点的话,那么我想说主要缺点是它们比梯度下降法复杂多了.特别是你最好不要自己实现L-BGFS、BFGS这些算法,除非你是数值计算方面的专家.
实际上,我不会建议你们编写自己的代码来计算数据的平方根,或者计算逆矩阵,因为对于这些算法，我还是会建议你直接使用一个软件库,比如说,要求一个平方根,我们所能做的就是调用一些别人已经写好用来计算数字平方根的函数.
现在让我们来说明,如何使用这些算法:
我们先举一个例子:
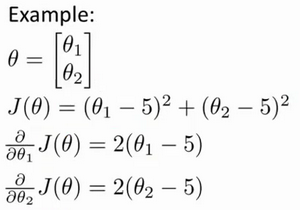
如上,你有一个含两个参数的问题，这两个参数是\(\theta_1\)和\(\theta_2\).因此,通过将代价函数最小化,你可以得到参数值\(\theta_1 = 5\)和\(\theta_2 = 5\).我们也可以得到\(J(\theta)\)的偏导求出来如下:
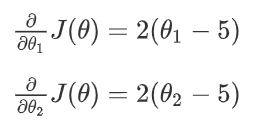
假设我们不知道\(\theta\)的最优值,但你想要应用高级优化算法来最小化代价函数\(J\).
后面涉及Octave 函数的就不写了,直接下一节吧.
5.7 多类别分类:一对多
在本节视频中,我们将谈到如何使用逻辑回归(logistic regression)来解决多类别分类问题,具体来说.我想通过一个叫做"一对多" (one-vs-all)的分类算法.
什么是多类别分类问题?让我们来看下面的例子:
(1) 第一个例子:假如说你现在需要一个学习算法能自动地将邮件归类到不同的文件夹里,或者说可以自动地加上标签,那么,你也许需要一些不同的文件夹,或者不同的标签来完成这件事,来区分开来自工作的邮件、来自朋友的邮件、来自家人的邮件或者是有关兴趣爱好的邮件,那么,我们就有了这样一个分类问题:其类别有四个,分别用\(y=1,2,3,4\)表示.
(2) 第二个例子:如果一个病人因为鼻塞来到你的诊所,他可能并没有生病,用y=1这个类别来代表;或者患了感冒,用y=2来代表;或者得了流感用y=3来代表
强调一下:y从1开始还是0开始并不重要.
我们可以比较一下二分类与多分类的数据集:
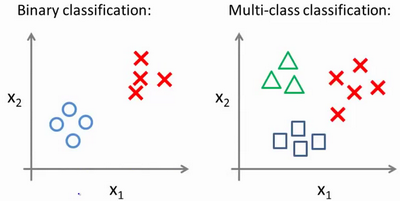
我们已经知道逻辑回归可以用来处理二分类的问题.但是这里如果我们利用一对多的思想,我们也可以将其应用在多分类的问题上.
下面将介绍如何进行一对多的分类原理,有时这个方法也被称为"一对余"方法:
现在我们有一个训练集,好比下图表示的有3个类别:我们用三角形表示y=1,方框表示y=2,叉叉表示y=3.我们下面要做的就是使用一个训练集,将其分成3个独立的二元分类问题.
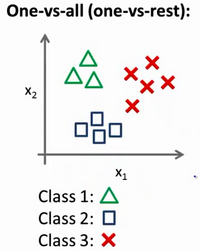
我们先从用三角形代表的类别1开始,实际上我们可以创建一个,新的"伪"训练集,类型2和类型3定为负类,类型1设定为正类,我们创建一个新的训练集,如下图所示的那样,我们要拟合出一个合适的分类器.
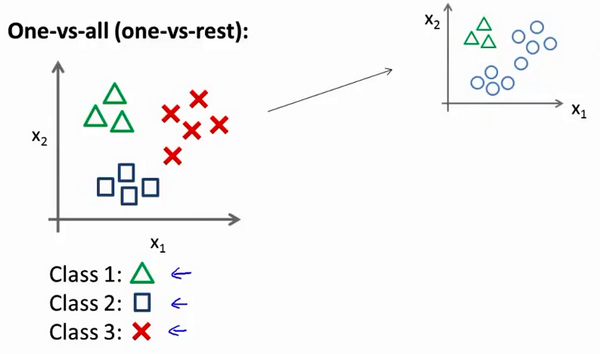
为了能实现这样的转变,我们将多个类中的一个类标记为正向类(\(y=1\)).然后将其他所有类都标记为负向类,这个模型记作\(h_{\theta}^{(1)}(x)\).接着,类似地第我们选择另一个类标记为正向类(\(y=2\)).再将其它类都标记为负向类,将这个模型记作\(h_{\theta}^{(2)}(x)\).依此类推.最后我们得到一系列的模型简记为:
最后,在我们需要做预测时,我们将所有的分类机都运行一遍,然后对每一个输入变量,都选择最高可能性的输出变量.
总之,我们已经把要做的做完了,现在要做的就是训练这个逻辑回归分类器:\(h_{\theta}^{(i)}(x)\),其中\(i\)对应每一个可能的\(y_i\).如果我们给出一个全新的\(x\)值,我们要做的就是在所有分类器里运行一遍,然后选择\(h_{\theta}^{(i)}(x)\)最大的\(i\).
你现在知道了基本的挑选分类器的方法,选择出哪一个分类器是可信度最高效果最好的,那么就可认为得到一个正确的分类,无论\(i\)是多少,我们都有最高的概率值,我们预测\(y\)就是那个值.这就是多类别分类问题,以及一对多的方法,通过这个小方法,你现在也可以将逻辑回归分类器用在多类分类的问题上.
