机器学习 吴恩达 第四章 笔记

四、多变量线性回归(Linear Regression with Multiple Variables)

  在本章节,我们要讨论一种新的线性回归形式.这种形式适用于多个变量(或者说多特征量).在我们之前讨论的线性回归,我们只有一个特征量(房屋面积),我们必须用此特征量来预测房屋价格.但现在我们有多种特征来预测.

4.1 多维特征

  现在我们对房价模型增加更多的特征,例如房间数楼层等、房屋年龄等,构成一个含有多个变量的模型.我们用\(x_1,x_2,x_3,x_4\)等来表示我们房屋的不同特征,然后仍然沿用\(y\) 来表示房屋价格.

  增添更多特征后,我们引入一系列新的注释:

• \(n\):特征的数量
• \(x^i\):第\(i\)个训练实例,是特征矩阵中的第\(i\)行,是一个向量(vector).
• \(x_j^{(i)}\):特征矩阵中第\(i\)行的第\(j\)个特征,也就是第\(i\)个训练实例的第\(j\)个特征.

  比方说,上图的\(x^{(2)}\)表示一个四维的向量:

  再比如说\(x_3^{(2)}\)表示第2行的第3个特征量:2
  既然有了多变量,那么假设的形式也变了:

  这个公式中有\(n+1\)个参数(\(\theta\))和\(n\)个变量.为了使得公式能够简化一些,引入\(x_0 = 1\),也就是代表\(x^{(i)}_0 = 1\),額外定义了第\(0\)个特征量,则公式转化为:

  所以特征向量\(X\)是一个有\(n+1\)维的向:

\[\begin{matrix} x_0 \\ x_1 \\ x_2 \\ ... \\ x_n \\ \end{matrix} \ \]

  如果把参数\(\theta\)也看作一个向量,那么\(\theta\)也是一个\(n+1\)维的向量.
  那么,由于它们都被看作向量,那么假设\(h\)可以写作:

\[h_{\theta}(x) = \theta^TX \]

  这是多特征假设,我们也可以称为多元线性回归.

4.2 多变量梯度下降

  在本节,我们将介绍如何赋值假设的参数\(\theta\),也就是如何使用梯度下降处理多元线性回归.

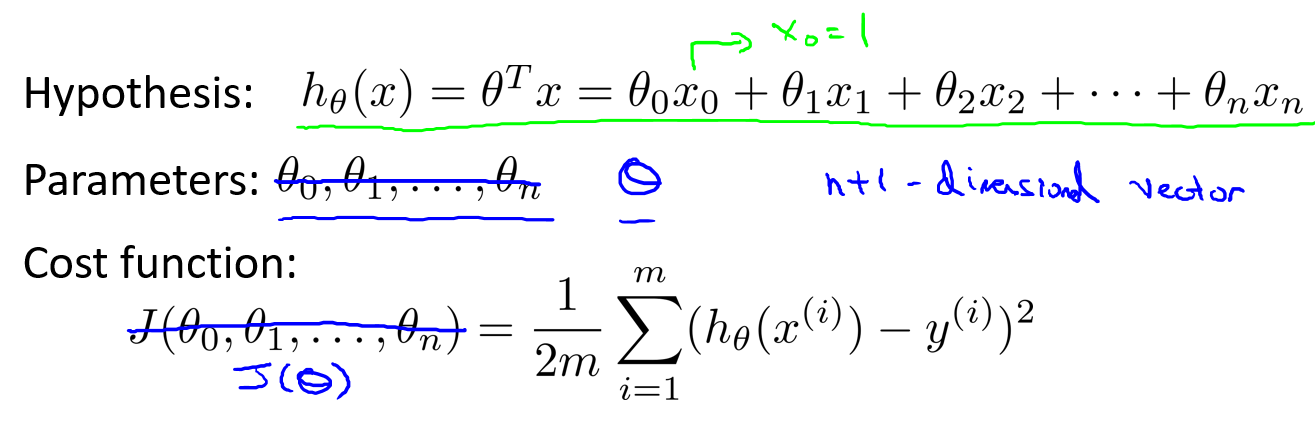
  在这里,我们不把\(\theta\)看作\(n+1\)个参数,而是将它们看作向量.那么,\(J(\theta)\)就是向量的函数.
  下面是多元参数的梯度下降:

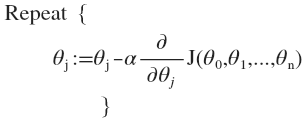
  接下来,我们需要理解梯度下降执行起来是什么样子:
  当线性回归的样本数只有\(1\)时,此时有点类似单元线性回归,只是我们求\(\theta_1\)偏导时,\(x^{(i)}\)在单元线性回归表示第\(i\)个样本,而在多元线性回归只能用\(x_1^{(i)}\)第\(i\)个样本的第1个参数.

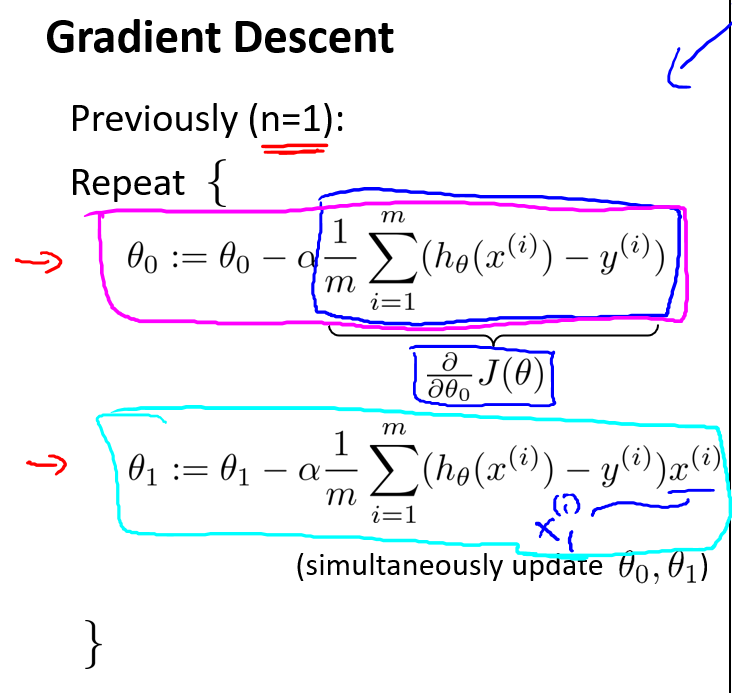
  但是当线性回归的样本数\(>=1\),此时我们就需要求出一个普遍适用的梯度下降收敛的法则.

  我们开始随机选择一系列的参数值,计算所有的预测结果后,再给所有的参数一个新的值,如此循环直到收敛.

4.3 梯度下降法实践1-特征缩放

  当我们有一个机器学习的多特征问题,如果能保证这些特征量都在相近的范围,这将帮助梯度下降算法更快地收敛.
  以房价问题为例,假设我们使用两个特征(这里不考虑第0个特征),房屋的尺寸和房间的数量;尺寸的值为0-2000平方英尺,而房间数量的值则是0-5,以两个参数分别为横纵坐标,绘制代价函数的等高线图能,看出图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛.

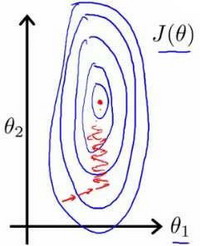
  当椭圆越瘦长,我们需要的迭代次数越多,这样才能找到一条通往全局最小值的路(每次下降都是沿着等高线垂直的方向走).
  当这种情况下,一种有效的方法就是进行特征缩放.

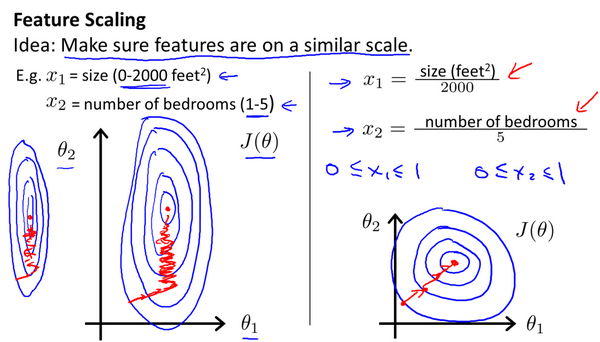
  我们尝试将所有特征的尺度都尽量缩放到-1到1之间,这样图形就会更加圆,我们也更容易找到通往全局最小值的路.
  因为\(x_0\)确定是\(1\),已经在范围内,所以不需要变化.
  请注意,是尽量缩放到$ [-1,1] $,所以不是一定要缩放到,所以范围相近也可以.

  [-100,100]太大了,而[-0.001,0.001]就太小了.一般老师是以竖线右边的为基准.当大于[-3,3]就需要注意,小于\([-\frac{1}{3},\frac{1}{3}]\)也需要注意.
  在特征缩放中,除了除以最大值外,我们也会采用均值标准化的做法,其中\(u_n\)是平均值,而\(s_n\)是标准差(或者范围即最大值-最小值),但实际上用最大值-最小值就可以了.

\[x_n = \frac{x_n - u_n}{s_n} \]

  特征缩放比较随意,但我们只需要将范围缩放至相近就可以了,并不需要太精确.

4.4 梯度下降法实践2-学习率

  本节我们将讲述如何debug梯度下降以及如何选择学习率\(\alpha\)
  一个debug方法是:在梯度下降运行的同时,绘制\(J(\theta)\)的最小值与迭代次数的图表,X轴是迭代次数:

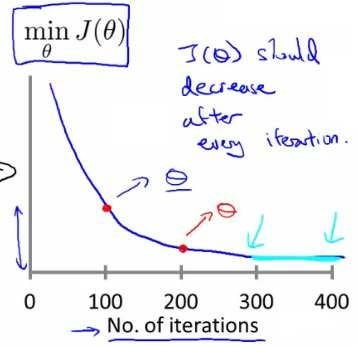
  当横坐标是100的时候,红点表示当迭代100次,参数\(\theta\)取某值时,\(J(\theta)\)能取到的最小值.
  如果梯度下降正常工作,那么每次迭代,成本最小值都会下降.并且通过曲线我们可以判断梯度下降是否收敛了.
  我们也可以写一些函数来判断梯度下降是否收敛,一个典型的例子是如果\(J(\theta)\)一步迭代后下降$ ＜ 10^{-3}$

  实际上面的阈值只要是一个很小的数,则说明收敛.但实际上要选择的阈值有点难挑选,因此老师这里建议我们采用绘图的方法.
  我们可以通过图像对学习率进行一些判断.比如如果\(J(\theta)\)呈如下图,那么通常意味着学习率选择的太大了,导致成本函数冲过了最小值,持续迭代就会在最小值的两边来回振荡(前提是代码没有错误).

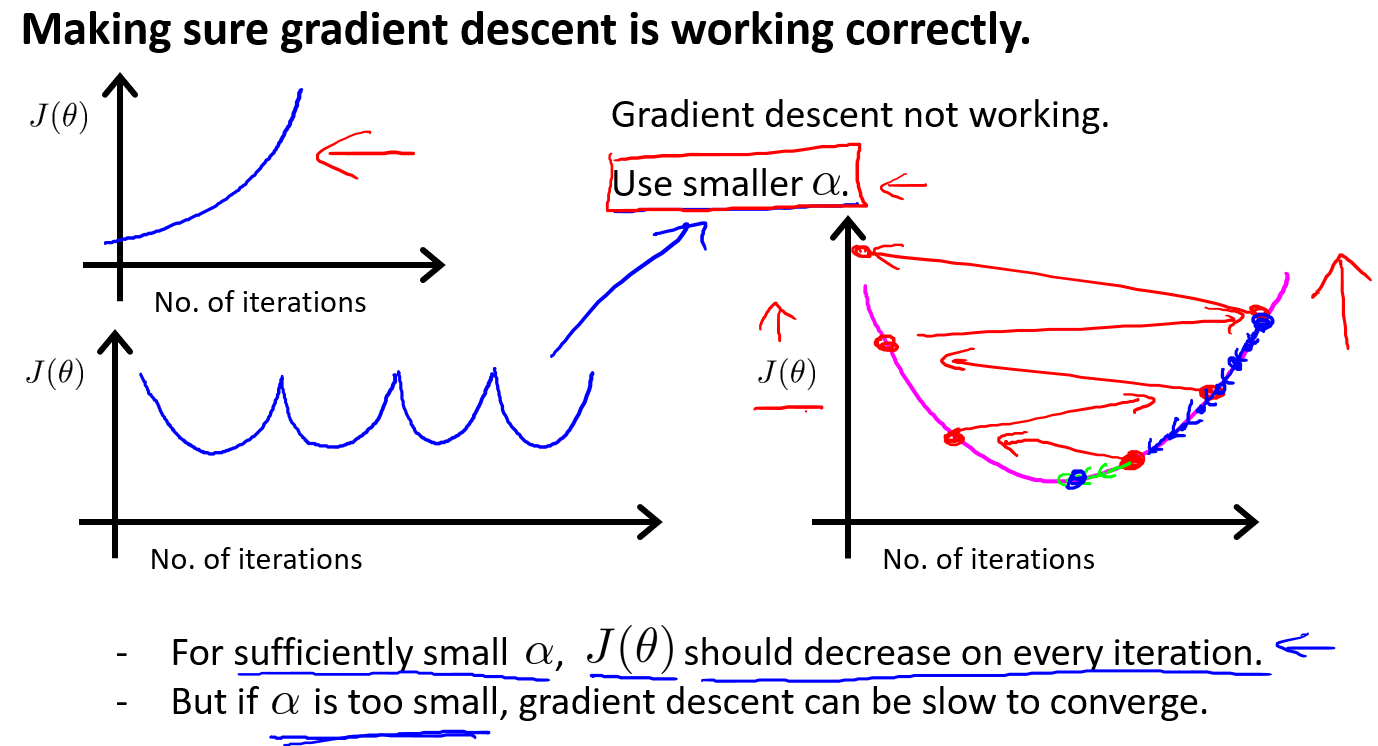
  如果我们看到的成本函数先下降后上升这样循环,这时的解决方法也是选择更小的学习率.
  实际上已经证明,如果学习率\(\alpha\)足够小,那么每次迭代后,成本函数\(J\)都会下降.当然太小就会下降很慢.

  通常可以考虑尝试些学习率:

\[\alpha = ...,0.01,0.03,0.1,0.3,1,3,10,... \]

  我们根据这些值绘制J与迭代次数的曲线,然后选择使得成本函数\(J(\theta)\)下降最快的值.通常我们会找到学习率太大的值和太小的值,然后从大学习率开始逐步下降.
  面对大数据样本,通常我们会选择一个大的学习率\(\alpha\),然后逐步减小查看效果.

4.5 特征和多项式回归

  以预测房价为例,假设有两个特征:房子临街的宽度和垂直宽度(类似模拟人生的土地面积\(30 \times 10\),30是临街宽度,10是垂直宽度).接下来,你可以建立一个这样的线性回归模型:

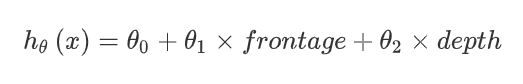
  而$ x_1 = frontage(临街宽度),x_2 = depth(垂直宽度), x = frontage \times depth = area(面积) $

  我们可以自己选择特征,也不一定要\(x_1\)和\(x_2\),比如上面使用面积\(x\)做特征值,那么假设就可以变成$ h(\theta) = \theta_0 + \theta_1 \times x $.
  与选择特征密切相关的一个想法是多项式回归.有时直线并不能拟合某些数据,所以我们需要曲线来拟合我们的数据.比如一个二次方模型:

\[h _\theta(x) = \theta_0+\theta_1x_1+\theta_2x_2^2 \]

但是二次函数是先降后升或先升后降,这种趋势与房子大小与房价的关系不太合理,所以也会用一个三次方模型:

\[h _\theta(x) = \theta_0+\theta_1x_1+\theta_2x_2^2+\theta_3x_3^3 \]

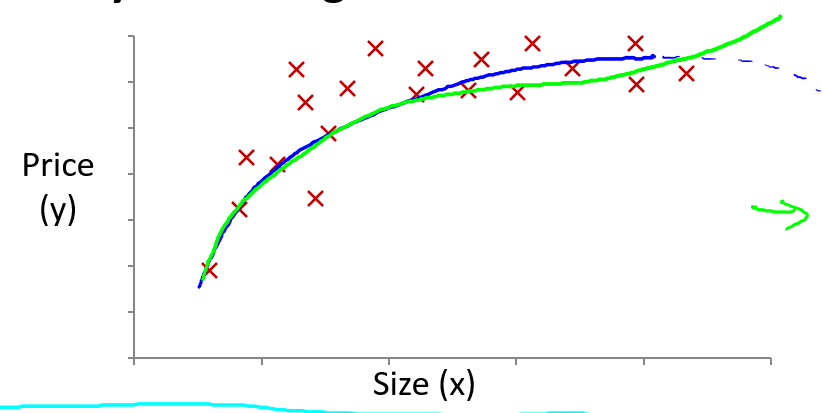
  如果我们想将之前的线性假设:

\[h _\theta(x) = \theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3 \]

转变为多元线性回归,比如三次线性回归,一个方法是将$x_1 = (size),x_2 = (size)^2,x_3 = (size)^3 \( 具体参考如下,将\)x$转换后,再运用线性回归的方法,我们最终可以将一个三次函数拟合到数据上:

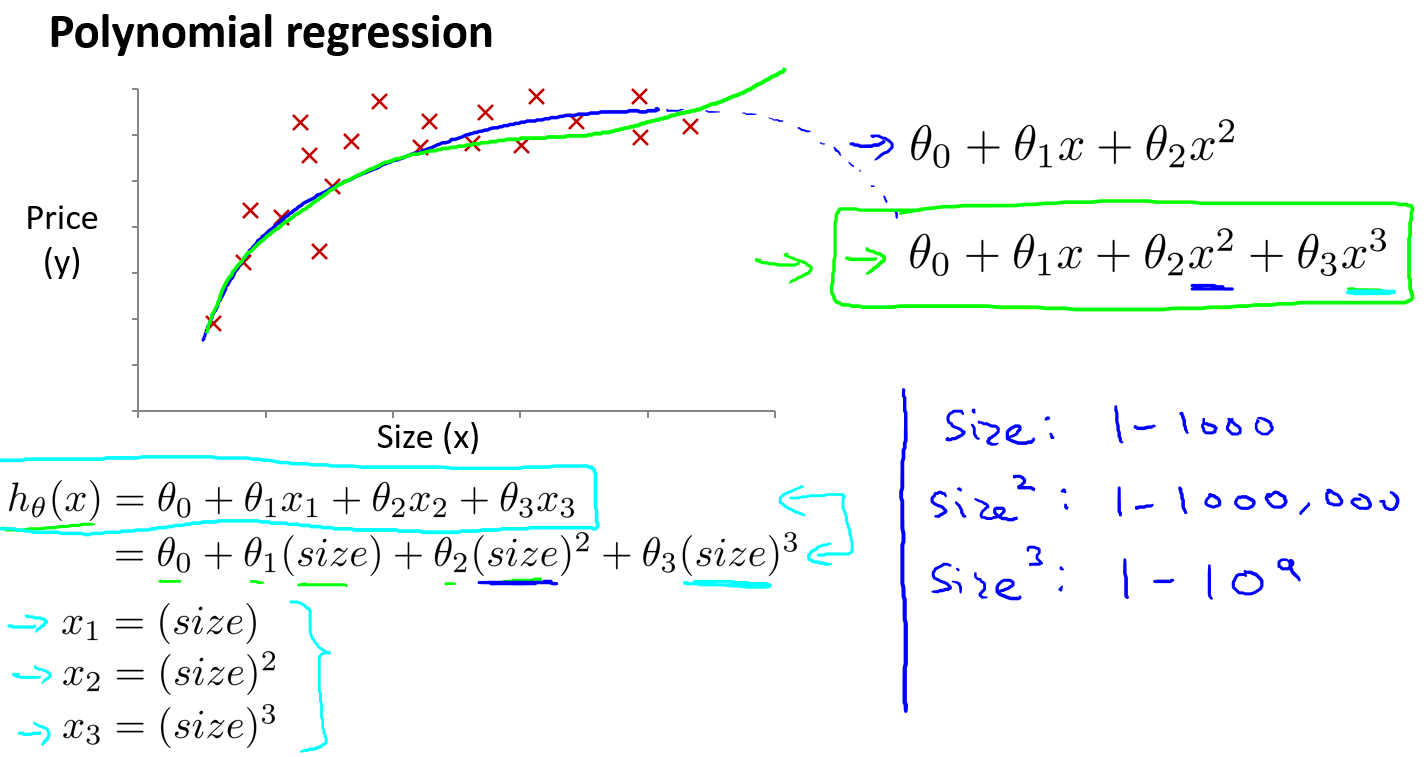
  注意:如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要.
  比如上面\(size\)的一二三次方,范围大小差距很大,只有通过特征缩放,才能将值的范围变得具有可比性.

  最后仍然是房价预测的例子,我们也不一定要选择是三次模型,下面的模型也可以作为参考:

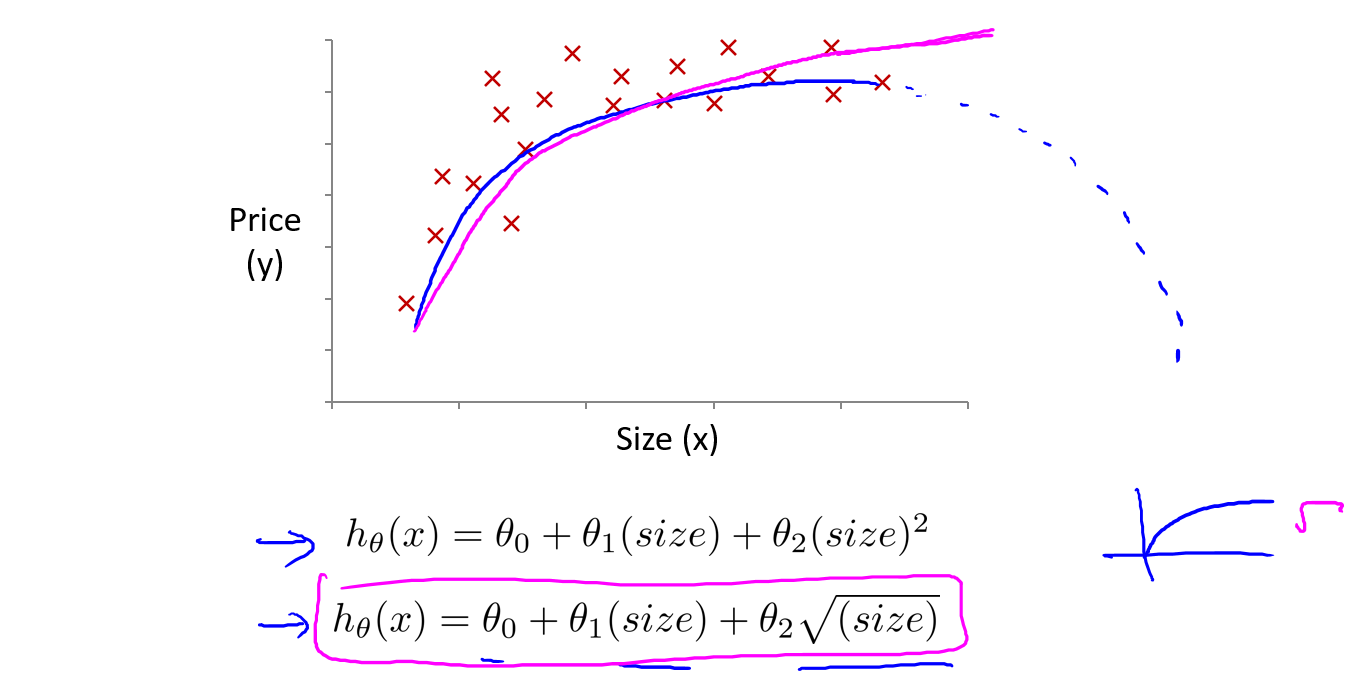
  我们根据数据图像的趋势判断来选择特征,有时可以选择出更好的模型.
  后面会谈到一些算法能够自动选择要使用什么特征.

4.6 正规方程

  对于某些线性回归问题,它会给我们更好的方法来求得参数\(\theta\)的最优值.正规方程可以避免梯度下降的多次迭代,它可以一次性求解\(\theta\)的最优值.
  我们通过下面的例子直观理解正规方程,假设有一个代价函数如下图所示,请注意\(\theta\)是实数不是向量:

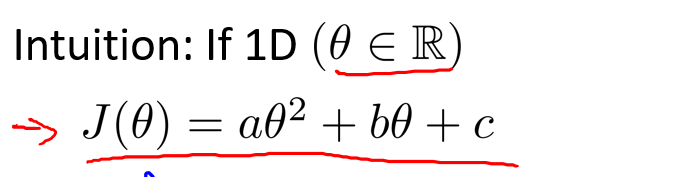
  求解上面函数的最小值的方法是将上面函数求导,得到导函数 = 0的\(\theta\)值,再代入原代价函数,这样就可以求解出最小值.
  延伸到原问题,\(\theta\)是一个向量,而代价函数是这个向量的函数.涉及微积分的一个求解\(J(\theta)\)的最小值的方法,就是对每个参数\(\theta_i\)求偏导,对偏导置0,再求出\(\theta_i\)的值.
  但是一个个求很费事,所以我们需要复习一些微积分的知识.

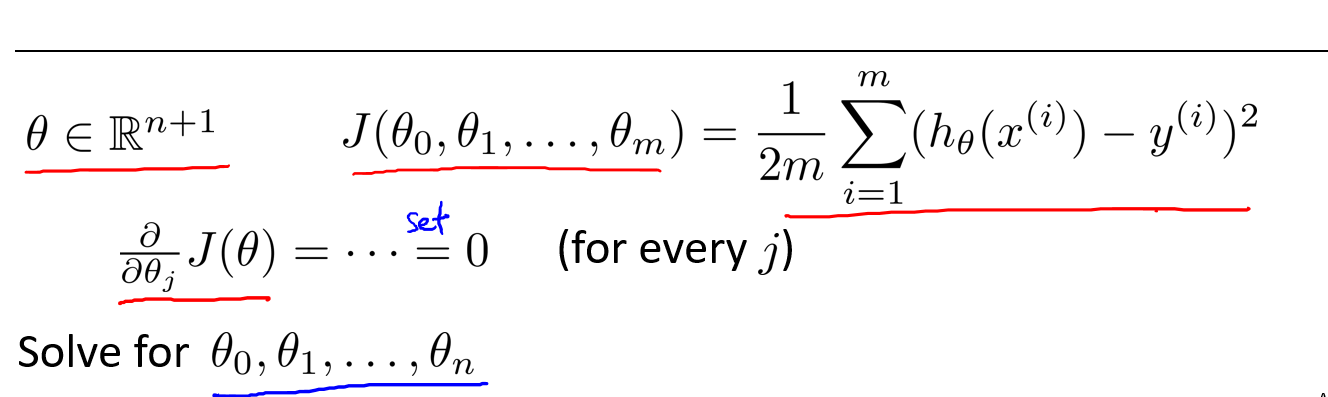
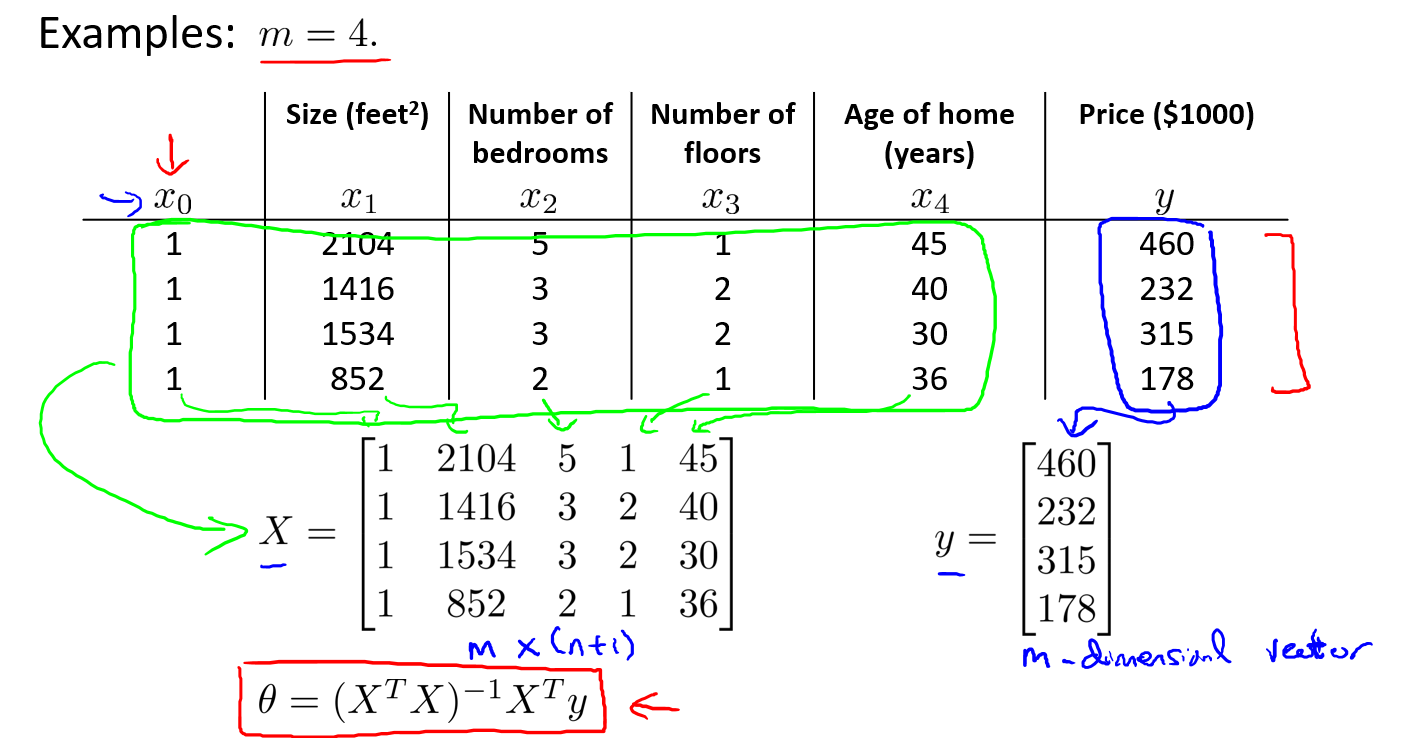
  以下面的房价预测为例,假设有4个训练样本,我们需要在数据集插入一列\(x_0\),这列的值全为1,并且我们需要构建一个矩阵X,这个矩阵包含了训练样本所有的特征值,再构建一个向量y,包含所有的输出值.

  接下来就有一个公式(正规方程):

\[\theta = (X^TX)^{-1}X^Ty \]

可以计算出向量\(\theta\).标T代表矩阵转置,上标-1代表矩阵的逆.
这里可以看推导过程,很详细Click
  将公式代入后,我们可以运用正规方程方法求解参数:

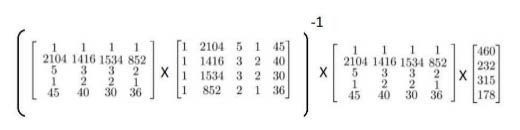
  通过一个样本\(x_{i}\)对应的是一个有\(n+1\)维的向量,我们想构建矩阵,就需要将向量转置作为一行的内容.
  如果我们采用正规方程的方法求最优值,那么就不需要进行特征缩放.
  接下来,我们对梯度下降和正规方程的方法进行对比,这样我们就知道何时应该选择哪种方法.

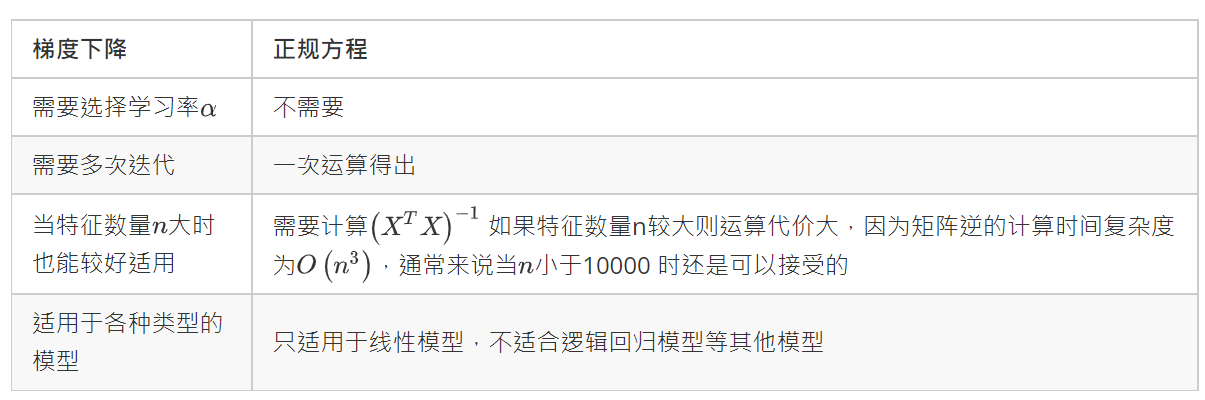
  梯度下降的方法适用性比正规方程广,比如逻辑回归的模型就不能使用正规方程的方法.

  这里列一下正规方程的Python实现:

#这里还是numpy array对象,如果转为matrix对象会更简单.
def normalEqn(X, y):
	X_inv = np.linalg.inv(np.dot(X.T,X))
	return np.dot(np.dot(X_inv,X.T),y)

4.7 正规方程及不可逆性(可选)

  我们要讲的问题如下,当计算\(\theta\)时,如果\(X^TX\)不可逆应该怎么处理:

\[\theta = (X^TX)^{-1}X^Ty \]

  在线性代数里,我们称那些不可逆矩阵为奇异或退化矩阵.问题的重点在于\(X^TX\)的不可逆的问题很少发生.
  那么什么情况会导致不可逆呢?这里没有通过数学的方式证明,但主要有两种情况会导致不可逆:

(1) 在样本中包含了多余的特征.例如,在预测住房价格时,如果\(x_1\)是以英尺为尺寸规格计算的房子,\(x_2\)是以平方米为尺寸规格计算的房子,同时,你也知道1米等于3.28英尺 (四舍五入到两位小数),这样,你的这两个特征值将始终满足约束:$$ x_1 = x_2 \times (3.28)^2 $$.实际上,你可以用这样的一个线性方程,来展示那两个相关联的特征值.这样就会导致$ X^TX$是不可逆的.

  你可以实际测试一下,这会导致X的行列式为0,所以不可逆.

(2) 在运行的训练集特征太多,这也会导致\(X^TX\)不可逆.具体来说,是m <= n时.例如,当m有10个的训练样本,n = 100即有100个特征时,要找到适合的\(n+1\)维向量\(\theta\),即101维的向量.也就是说,我们要使用10个样本来配置101个参数\(\theta\).这样的数据还是有点少的.
  一种直观的理解方式就是当方程的个数<方程的未知数,则有无穷多个解.此时方程构成的矩阵必然相关.
  一种方法解决m <= n的问题就是删除某些特征.还有一种正规化(后面讨论)的方法,它可以让你使用很多的特征来配置很多参数,即使有一个很小的数据集.

  总结:如果你发现\(X^TX\)是奇异矩阵,也即是不可逆的.可以考虑这么做:首先,看特征值里是否有一些多余的特征,比如某些线性相关的特征,如果有则考虑删除其中一个.如果没有多余的特征,就会检查特征的数量,如果数量实在太多,且少一点特征不影响的话,可以考虑删除一些特征.或者考虑正规化的方法.