机器学习by周志华 第一章习题

1.1 表1.1中若只包含编号为1和4的两个样例，试给出相应的版本空间

  很简单我就不写了。

1.2 与使用单个合取式来进行假设表示相比，使用“析合范式”将使得假设空间具有更强的表达能力，例如：

  好瓜←→ ((色泽=)∧（根蒂=蜷缩）∧（敲声=)）∨（（色泽=乌黑）∧(根蒂=*）∧(敲声=沉闷））
  会把"(色泽=青绿)∧（根蒂=蜷缩）∧（敲声=清脆)”以及“(色泽=青绿)∧（根蒂=蜷缩）∧（敲声=清脆)"都分类为"好瓜"。若使用最多包含k个合取式的析合范式来表达下表西瓜分类问题的假设空间，试估算共有多少中可能的假设。

  答案参考这篇文章1.2详细参考。这里只是针对这篇博客再进行解释。不考虑通配符*,只考虑色泽={乌黑、青绿},根蒂={蜷缩,硬挺,稍蜷},敲声={浊响、清脆、沉闷}。这种具体的取值有18个。
  当我们\(k\)=1时,也就是具体取值只有一个正确,那么有18种可能。
  当我们\(k\)=2时,也就是具体取值只有2个正确,就是在这18种可能里,取出两个作为正确的可能,也就是\(C_{18}^2\)
  后面无需举例,只是将2换成\(k\)的不同取值即可.

1.3 若数据包含噪声，则假设空间中有可能不存在与所有训练样本都一致的假设。在此情形下，设计一种归纳偏好用于假设选择

  当这种情况下,符合大多数样本数据但一小部分不符合的假设可以不去除,因此样本数据存在噪声(即错误或者异常)。

1.4 本章1.4节在论述“没有免费的午餐”定理时，默认使用了“分类错误率”作为性能度量来对分类器进行评估。若换用其他性能度量 ，则式（1.1）将改为

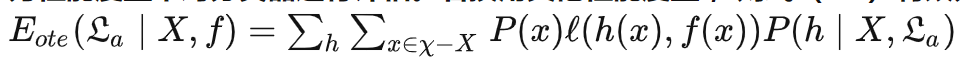
  试证明“没有免费的午餐定理”仍成立。

  下面的视频讲解说得很好,可以配合后面的步骤理解1.4 视频讲解