Climbing the Hill HDU - 4315

原题链接
考察:博弈论
思路:
  这道题像上题一样解释阶梯博弈会发现行不通,因为0位置可以被多个点占据,而上题所有位置都是一个棋子.
  那么怎么解呢?博弈论的快速解法就是去找必败态.我们可以发现:

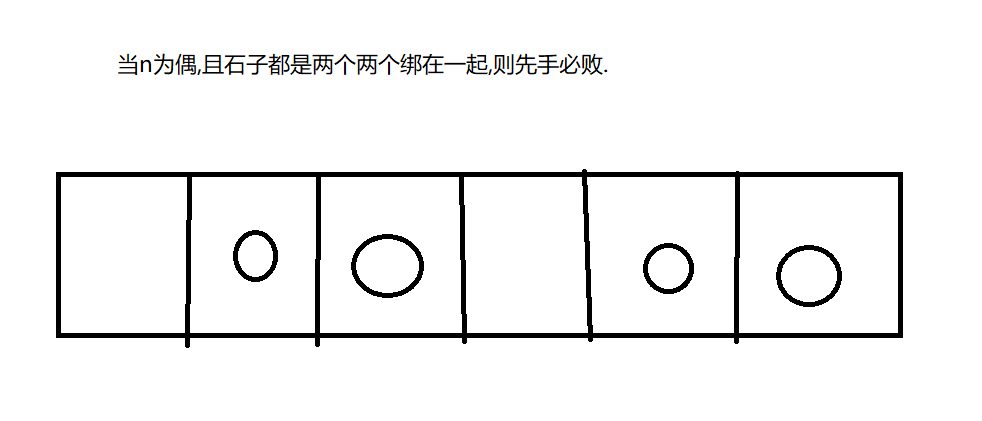
  先手只能移动一组里左边的石子,如果k在组里的第二个,那么先手必败.
  如果k在组里的第一个呢?

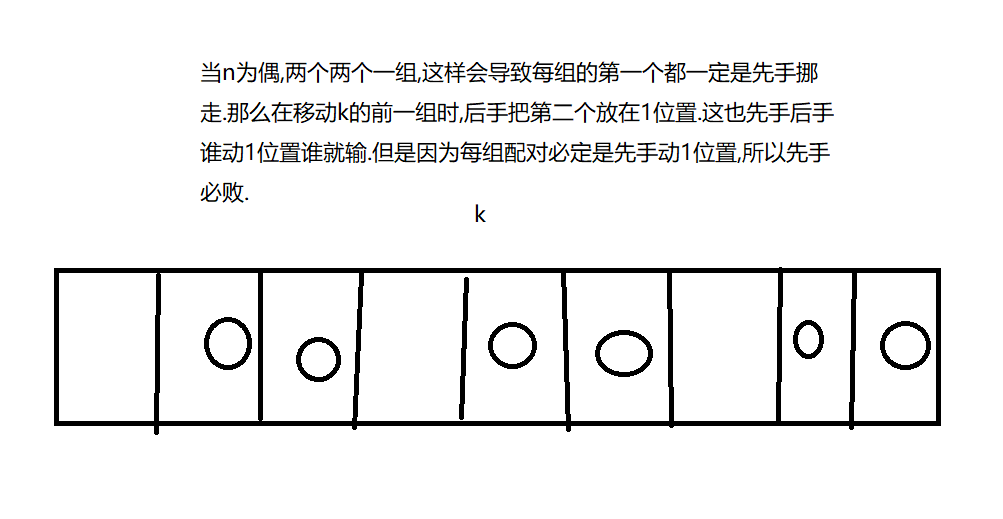
  接下来讨论n为奇,从后往前配对,第1个棋子只能和0号位置配对,可以发现先手必败态也是组内之间可移动距离为0.
  但是这也就会发现特殊情况:

1. k==1,先手必胜.
2. k==2&&n%2==1 如果我们直接把第1个放在山顶处,就会导致后手直接获胜.此时我们发现如果我们把第1个放在1位置,此时还是先手必败态.

  发现这么多先手必败态有什么用呢?取石子游戏里,所有石子数 = 0,石子堆异或和 = 0为判断先手负的依据.而此处,可以把组内可移动距离看成石子堆,移动第二个棋子就是取石子,移动第一个棋子就移动第二个棋子保持不变.但是注意特殊情况2,1号棋子与0号位置距离-1才是必败态.

Code

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int a[N],n,b[N],k;
int main()
{
	while(scanf("%d%d",&n,&k)!=EOF&&(n+k))
	{
		for(int i=1;i<=n;i++) scanf("%d",&a[i]);
		if(k==1) {puts("Alice"); continue;} 
		sort(a+1,a+n+1);
		int res =0;
		a[0] = -1;
		if(k==2&&(n&1)) a[0]++;
		for(int i=n;i>=1;i-=2)
			res^=a[i]-a[i-1]-1;
		if(res) puts("Alice");
		else puts("Bob");
	}
	return 0;
}