AcWing 344. 观光之旅
考察:Floyd
思路:
考察Floyd算法应用之最小环.在应用Floyd之前我们先了解Floyd的本质.
1 for(int k=1;k<=n;k++)//起点到终点之间经过1~k点 2 for(int i=1;i<=n;i++)//枚举起点 3 for(int j=1;j<=n;j++)//枚举终点 4 g[i][j] = min(g[i][k]+g[k][j],g[i][j]);
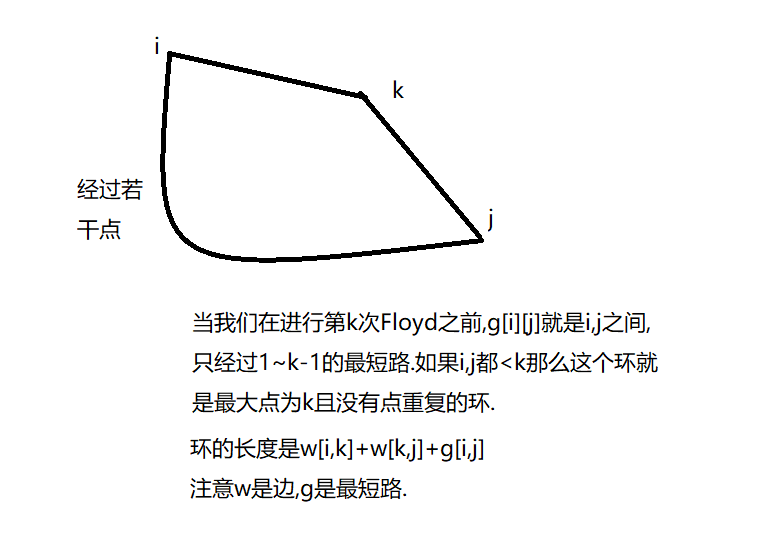
可以发现g[i][j]收缩值都是依靠i与k ,j与k的边.所以当k = m时,此时g[i][j]的最短路途径点最大就是K.
我们知道Floyd算法的思想是动态规划.那么最小环是否能根据dp来求?
我们将最小环集合以途径点最大不超过k来划分.那么这就和Floyd算法产生了联系.我们假设当前起点为i,终点为j,那么:
1 #include <iostream> 2 #include <cstring> 3 #include <vector> 4 using namespace std; 5 const int N = 110,M = 20010,INF = 0x3f3f3f3f; 6 typedef long long LL; 7 int n,m,g[N][N],d[N][N],path[N][N]; 8 int res = INF; 9 vector<int> v; 10 void dfs(int l,int r) 11 { 12 int k = path[l][r]; 13 if(!k) return; 14 dfs(l,k); 15 v.push_back(k); 16 dfs(k,r); 17 } 18 void get_path(int i,int j,int k) 19 { 20 v.clear(); 21 v.push_back(k); 22 v.push_back(i); 23 dfs(i,j); 24 v.push_back(j); 25 } 26 void floyd() 27 { 28 memcpy(d,g,sizeof g); 29 for(int k=1;k<=n;k++) 30 { 31 for(int i=1;i<k;i++) 32 for(int j=i+1;j<k;j++)//还没更新前 d[i][j]包含 1~k-1 g[i][k]与g[k][j]是原图的边 33 if(res>(LL)g[i][k]+g[k][j]+d[i][j])//i,j路段的中间点是k 34 { 35 res = (LL)g[i][k]+g[k][j]+d[i][j]; 36 get_path(i,j,k); 37 } 38 for(int i=1;i<=n;i++)//i,j最短路中,包含1~k的最小值 39 for(int j=1;j<=n;j++) 40 if(d[i][j]>d[i][k]+d[k][j]) 41 { 42 d[i][j] = d[i][k]+d[k][j]; 43 path[i][j] = k; 44 } 45 } 46 } 47 int main() 48 { 49 scanf("%d%d",&n,&m); 50 memset(g,0x3f,sizeof g); 51 while(m--) 52 { 53 int a,b,c; scanf("%d%d%d",&a,&b,&c); 54 if(a==b) continue; 55 g[a][b] = g[b][a] = min(g[b][a],c); 56 } 57 for(int i=1;i<=n;i++) g[i][i] = 0; 58 floyd(); 59 if(res==INF) puts("No solution."); 60 else 61 for(auto it:v) printf("%d ",it); 62 return 0; 63 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号