P1073 [NOIP2009 提高组] 最优贸易
考察:最短路+dp
写这道题的时候脑子很乱...没想多久就看了题解...忏悔
写题效率真的太低了...
引入:
dp是基于拓扑序的图论最短(最小值)或最长(最大值)的问题.dp的每一个状态都能推导它后面的一个状态,这种有顺序的遍历就是拓扑序.但是对于不是拓扑序的dp问题应该如何求解?
思路:
这道题很像股票买卖.但是和股票买卖不同的是每个点之间的递推关系不是线性的.也就是说,只有u与v之间有路径,f[v]才能由f[u]推来.并且这道题每个点都可以去任意多次.
比较直观的想法就是1~n之间的互通的路径中,找到一个价格最低的点和价格最高的点.但这样比较难写,因为价格最高/低的点不一定能到1或n.为了n与1能连通在一起,我们可以设f[0][i]表示从1开始所有能到i的点中,价格最少.f[1][i]表示所有从n开始能到i的点中,价格最多.那么结果就是枚举f[1][i]-f[0][i]求最大值.
注意这图上有环,不能用树形dp的形式dfs(u,father).
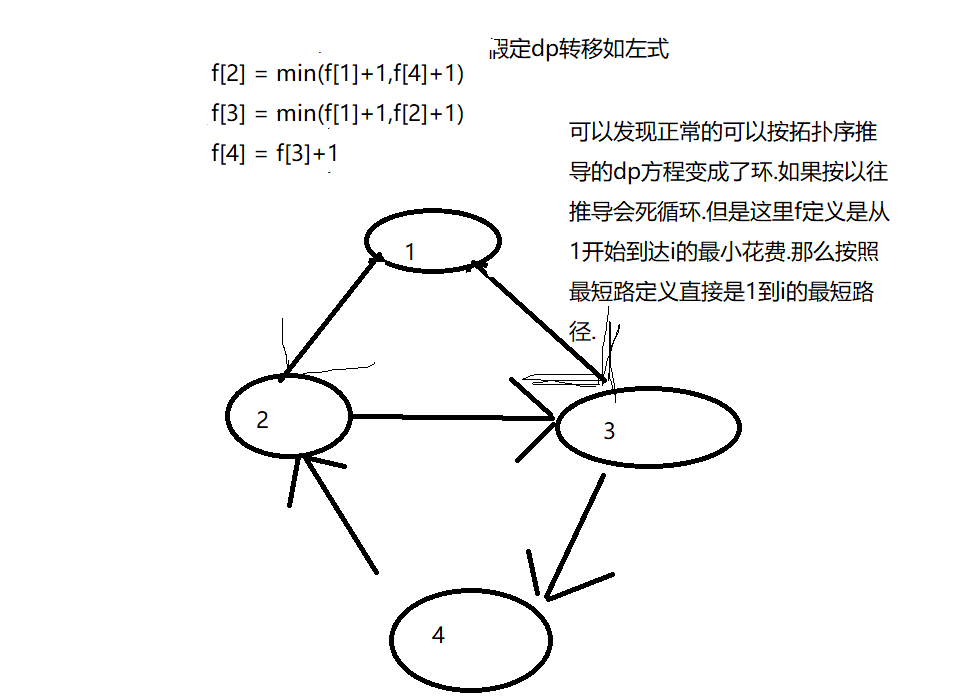
如何解带环的dp方程如图,如果是求最大值就是最长路.这道题也可以用记忆化搜索.
注意求最短路不能用Dijkstra.因为Dijkstra算法是第一次出队就确定了最短路,这里我们从1出发不能确定2或者3出队就是最短路.
所以用SPFA算法+dp求解.
1 #include <iostream> 2 #include <cstring> 3 #include <vector> 4 #include <queue> 5 using namespace std; 6 const int N = 100010,M = 500010; 7 int n,m,price[N],f[2][N]; 8 vector<int> maxn[N],minv[N]; 9 bool st[N]; 10 void spfa(int s) 11 { 12 memset(f[0],0x3f,sizeof f[0]); 13 queue<int> q; 14 st[s] = 1; 15 q.push(s); 16 while(q.size()) 17 { 18 int u = q.front(); 19 q.pop(); 20 st[u] = 0; 21 f[0][u] = min(price[u],f[0][u]); 22 for(int i=0;i<minv[u].size();i++) 23 { 24 int v = minv[u][i]; 25 if(f[0][v]>f[0][u]) 26 { 27 f[0][v] = f[0][u]; 28 if(!st[v]) q.push(v),st[v] = 1; 29 } 30 } 31 } 32 } 33 void spfa_2(int s) 34 { 35 queue<int> q; 36 st[s] = 1; 37 q.push(s); 38 while(q.size()) 39 { 40 int u = q.front(); 41 q.pop(); 42 st[u] = 0; 43 f[1][u] = max(price[u],f[1][u]); 44 for(int i=0;i<maxn[u].size();i++) 45 { 46 int v = maxn[u][i]; 47 if(f[1][v]<f[1][u]) 48 { 49 f[1][v] = f[1][u]; 50 if(!st[v]) q.push(v),st[v] = 1; 51 } 52 } 53 } 54 } 55 int main() 56 { 57 scanf("%d%d",&n,&m); 58 for(int i=1;i<=n;i++) scanf("%d",&price[i]); 59 while(m--) 60 { 61 int a,b,c; scanf("%d%d%d",&a,&b,&c); 62 maxn[b].push_back(a); 63 minv[a].push_back(b); 64 if(c==2) 65 { 66 maxn[a].push_back(b); 67 minv[b].push_back(a); 68 } 69 } 70 spfa(1); 71 spfa_2(n); 72 int res = 0; 73 for(int i=1;i<=n;i++) res = max(res,f[1][i]-f[0][i]); 74 printf("%d\n",res); 75 return 0; 76 }


